Көрсеткіштік және логарифмдік функциялар

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

І-тарау. Көрсеткіштік және логарифмдік функциялар.

§1. Көрсеткіштік функция. Оның қасиеттері және графигі.

Анықтама: у = $a^{х}$ , α > 0, α ≠ 1 формуласы арқылы берілген функцияны көрсеткіштік функция деп атайды.

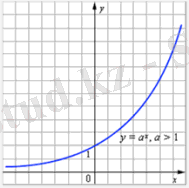
1 сурет.

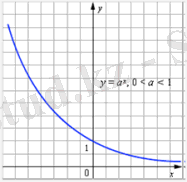
2 сурет.

Мұндағы, α саны - көрсеткіштік функцияның негізі, ал тәуелсіз айнымалы x - дәреженің көрсеткіші.

Табиғатта және адам өмірінде кейбір шамалардың белгілі бір шамаға олардың тұрақты аралықтағы қатынасы уақытқа тәуелді болмайтындай өзгеретін процестердің көп саны бар. Олардың ішінде заттардың радиоактивті ыдырауы, банктік шоттағы соманың өсуі және т. б. Бұл процестердің барлығы экспоненциалды функциямен сипатталады.

Көрсеткіштік функцияның негізгі қасиеттері төмендегідей:

Анықталу облысы - барлық нақты сандар жиыны, яғни x € R;
Мәндер жиыны - барлық оң нақты нақты сандар жиыны, яғни у €R+R_{+};
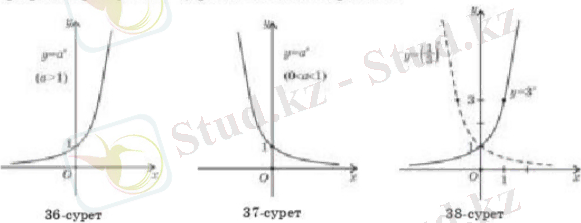
Негізі α > 1 болғанда функция анықталу облысында өспелі, ал 0 < α < 1 болғанда кемімелі функция;
Барлық x € R нақты сандар жиынында у =axa^{x}(α > 0, α ≠ 1) функциясы үзіліссіз;
Кез келген α > 0 үшіна0а^{0}= 1, демек, у =axa^{x}графигі координаталары (0; 1) болатын нүкте арқылы өтеді.

Көрсеткіштік функция үшін х және у-тің кез келген нақты мәндерінде мына теңдіктер орындалады:

$a^{х}$ × $a^{у}$ = $a^{x + y}$ ; $\frac{а^{х}}{а^{у}}$ = $a^{x - y}$ ; ${(ab) }^{x}$ = $a^{x} \times \ b^{x}$ ; ${(\frac{a}{b}) }^{x}$ = $\frac{a^{x}}{b^{x}}$ ; ${{(a}^{x}) }^{y}$ = $a^{xy}$ .

Функцияның жоғарыда аталған қасиеттерін дәлелдейік.

Дәлелдеу.

1) Негізі α > 0 болғанда, х - тің кез келген мәні үшін $а^{х}$ дәрежесін есептеуге болады. Олай болса, y = $а^{х}$ функциясының анықталу облысы - барлық нақты сандар жиыны.

2) у = $а^{х}$ , α > 0, α ≠ 1 функциясының мәні кез келген х нақты саны үшін оң сан. Демек, y = $а^{х}$ функциясының мәндер жиыны барлық оң нақты сандар жиыны болады.

3) Ох осінің бойынан кез келген $х_{1}$ және $х_{2}$ ( $х_{1\ \ }$ < $х_{2}$ ) нүктелерін (сандарын) алсақ, осы екі нүктеге сәйкес келетін фукнция мына мәндерді қабылдайды: $у_{1}$ = $a^{x_{1}}$ , $y_{2}$ = $a^{x_{2}}$ .

α>1 жағдайында кіші аргументке функцияның кіші мәні, үлкен аргументке функцияның үлкен мәні сәйкес болғандықтан, $a^{x_{1}}$ < $a^{x_{2}}$ . Осы заңдылық функцияның анықталу облысының жиынындағы кез келген екі нүкте үшін орындалады. Олай болса, α > 1 болғанда у = $a^{x}$ функциясы - өспелі функция.

Көрсеткіштік функцияның негізі 0 < α < 1 болғанда жоғарыда айтылған заңдылық керісінше орындалады, кіші аргументке функцияның үлкен мәні, үлкен аргументке функцияның кіші мәні сәйкес болғандықтан $a^{x_{1}}$ > $a^{x_{2}}$ . Демек, 0 < α < 1 аралығында y = ах функциясы - кемімелі функция.

Мысал ретінде y = $3^{х}$ және y =( ${\frac{1}{3}) }^{х}$ функцияларының графигін қарастырайық.

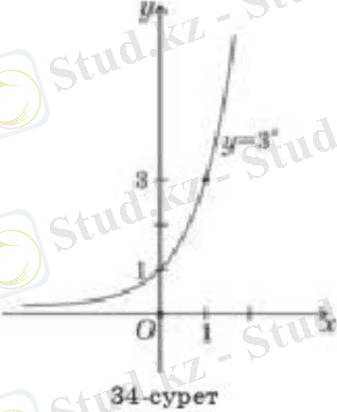
I. y = $3^{х}$ функциясының графигін салу үшін төмендегі кестені құрамыз:

-3

-2

-1

х: y =

3^{х}

-3:

\frac{1}{27}

-2:

\frac{1}{9}

-1:

\frac{1}{3}

0: 1

1: 3

2: 9

3: 27

(-3; $\frac{1}{27}$ ), (-2; $\frac{1}{9}$ ), (-1; $\frac{1}{3}$ ), (0; 1), (1; 3), (2; 9), (3; 27) нүктелерін координаталық жазықтыққа түсіргеннен кейін оларды қоссақ,

y = $3^{х}$ функциясының графигін аламыз. (3-сурет) .

Графиктен берілген функцияның өспелі функция екенін байқаймыз.

II. y = $({\frac{1}{3}) }^{х}$ функциясының графигін салу үшін мына 3-сурет

кестені құрамыз:

-3

-2

-1

х: y =

({\frac{1}{3}) }^{х}

-3: 27

-2: 9

-1: 3

0: 1

\frac{1}{3}

\frac{1}{9}

\frac{1}{27}

(-3; 27), (-2; 9), (-1; 3), (0; 1), (1; $\frac{1}{3}$ ), (2; $\frac{1}{9}$ ), (3; $\frac{1}{27}$ ) нүктелерін координаталық жазықтыққа түсіріп және оларды қоссақ, y = $({\frac{1}{3}) }^{х}$ функциясының графигін аламыз. (4-сурет) .

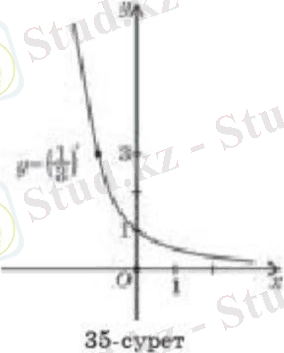Графиктік берілген функцияның анықталу облысында кемімелі екенін көреміз.

Енді y = $а^{х}$ , α > 0, α ≠ 1 функциясының графигі 5-суретте, ал 0 < α < 1 болғандағы графигі 6-суретте көрсетілген.

y = $3^{х}$ және y = $({\frac{1}{3}) }^{х}$ көрсеткіштік функцияларының графиктерін бір координата-

4-сурет

лық жазықтыққа салайық (7-сурет) . Суреттен аталған функциялардың графиктері Оу осіне қарағанда симметриялы екенін көреміз. Осыдан мына тұжырымды аламыз: егер екі көрсеткіштік функцияның негіздері өзара кері сандар болса, онда ол функциялардың графиктері Оу осіне қарағанда симметриялы.

5-сурет 6-сурет 7-сурет

4) Көрсеткіштік функцияның үзіліссіздігін дәлелдейік.

y = $а^{х}$ , α > 0, α ≠ 1 функциясы берілсін. Аргумент х-ке ∆х өсімше берсек, аргумент өсімшесіне сәйкес функция да өсімше қабылдайды:

∆у = $а^{х + \mathrm{\Delta}y}$ - $а^{х}$ = $а^{х}$ × $а^{\mathrm{\Delta}х}$ - $а^{х}$ = $а^{х}$ ( $а^{\mathrm{\Delta}х}$ - 1) .

енді осы өсімшенің ∆х→0 ұмтылғандағы шегін табайық:

∆х→ $а^{х}$ ×( $а^{0}$ - 1) = 0.

Аргументтің шексіз аз өсімшесіне функцияның да шексіз аз өсімшесі сәйкес келеді. Осы заңдылық y = $а^{х}$ функциясы үшін аргументтің анықталу облысының кез келген нүктесін орындалады. Демек, y = $а^{х}$ функциясы өзінің анықталу облысының кез келген нүктесінде үзіліссіз.

1 - мысал:

y = $5^{x - 1}$ +1 функциясының графигін салайық.

Шешуі: Алдымен y = $5^{x}$ функциясының графигін салу керек. Ол үшін a = 5 > 1 екенін ескеріп 7 - сурет бойынша барлық нақты сандар жиынында өспелі функцияның графигін жүргіземіз. Одан кейін салынған графикті Ох осі бойымен бір бірлікке оң бағытта параллель көшіреміз. Шыққан графикті Оу осі бойымен бір бірлікке доғары параллель көшіреміз. (8-сурет) .

2 - мысал:

${0, 27}^{4}$ және ${0, 27}^{10}$ сандарын салыстырайық.

Шешуі: Берілген сандардың негіздері бірдей және 0, 27-ге тең. Осы негізді - санымен салыстырамыз: 0, 27 < 1, бұл жағдайда көрсеткіштік функция кемімелі. Демек, кіші аргументке функцияның үлкен мәні сәйкес. Сондықтан ${0, 27}^{4}$ > ${0, 27}^{10}$ .

Жауабы: ${0, 27}^{4}$ > ${0, 27}^{10}$ .

3 - мысал:

y = $2^{x}$ және y = $х^{2}$ функцияларының графиктері неше нүктеде қиылысатынын көрсетейік.

Шешуі: Ол үшін бір координаталық жазықтыққа y = $2^{x}$ және y = $х^{2}$ функцияларының графиктерін саламыз. Бірінші функция көрсеткіштік функция және негізгі 1-ден үлкен. Демек, y = $2^{x}$ функциясының графигі (0; 1) нүктесі арқылы өтетін және R-де өспелі қисық. Ал y = $х^{2}$ функциясының графигі төбесі (0; 0) нүктесі болатын, тармақтары жоғары бағытталған парабола. Графиктері А және В нүктелерінде қиылысады (40-сурет) .