Математикалық физика теңдеулері

1. Пән туралы ақпарат Математикалық физика теңдеулері

2. Пәннің қысқаша сипаттамасы.

Курстың мақсаты : Математикалық физика теңдеулері басқа математикалық әдістерді, математика және физика салаларын зерттеп үйренуге дайындау. Студенттердің логикалық ойлау, математикалық пайымдау дәрежелерін және математикалық мәдениетін физика, техника, жаратылыстану ғылымдарында кездесетін есептер мен проблемаларды шеше білу деңгейіне жеткізу.

Пәннің міндеті. Бұл пәннің математикалық аппаратының дұрыстығы, тұтастығы, мықтылығы біріншіден қатаң логикалық құрылымына байланысты болса, екіншіден олар практика жүзінде тексеріліп, пайдалланылып отырады. Теориялық негіз болып саналатын дербес туынды дифференциялдар теңдеулерінің белгілі топтарына қойылатын Коши және шекаралық есептерінің шешімдерінің болуымен олардың жалғыздығы туралы.

Курсқа сипаттама. Табиғаттың объективті заңдарын сапалық жағынан зерттейтін физика ғылымы математиканың іргелі ұғымдарына сүйенеді, сонымен бірге математика заңдылықтарды сандық көрсеткіштермен толықтырады. Макро және микро әлемдерде жүріп жатқан өзгерістер мен құбылыстарды әр жақты көзқараста үрлі ғылымдар саласы ( физика, механика, биология, химия т. с. с. ) зерттеулерімен қатар, олардың математикалық моделдерін дербес туынды дифференциалдық теңдеулер жүйесімен өрнектеуге болады. Бұл теңдеулерді математикалық физика теңдеулері деп атайды, ал олардың шешімдері болып жатқан құбылыстардың заңдылығын көрсетеді.

Математикалық физика теңдеулерінің әдістері мен теориялық нәтижелерін пайдалану мақсатында, ең алдымен зерттелуші облыс үшін маңызды шамаларды белгілеп алу керек. Содан кейін осы шамаларға байланысты белгілі қисындар мен заңдылықтар негізінде қосымша шарттар анықталуы тиіс. Сонда ғана белгісіз шамалар дифференциялдық теңдеулерден иабылады және олар бір мәнді болады. Атап өтетін жәйт, математикалық физиканың кез келген бір ғана есебі әр түрлі құбылыстардың, заңдылықтардың моделі бола алады.

3. Пререквизиттер: Пәнді меңгеру үшін студенттің мектеп курсы көлеміндегі математика бағдарламасын және математикалық талдау, алгебра, аналитикалық геометрия, дифференциалдық теңдеулер, кешенді айнымалы функциялар теориясы, функционалдық талдау, интегралды теңдеулер пәндерін жетік білгені жөн. Жалпы алғанда студенттің математикалық білімі жеткілікті деңгейде болуы тиіс.

4. Постреквизиттер: (оқытылатын пәннен алған білімдері қолданылатын пәндер тізімі) : математикалық физиканың теңдеулері, функциялар теориясы сандық әдістер, тиімділеу әдістері және операциялық зерттеулер, функционалдық анализ және т. б.

5. Күнтізбелік-тақырыптық жоспар.

6. Дәріс сабақтарының мазмұны

1-дәріс. Кіріспе. Екінші ретті дербес туындылы теңдеулерді классификациялау және канондық түрге келтіру.

Дәрістің мақсаты: Математикалық физика теңдеулеріне және оның негізгі ұғымдарына анықтама беру.

Тақырыптың негізгі сұрақтары:

1) Математикалық физика есептерінің қойылуы. Анықтама.

2) Екінші ретті дербес туындылардағы теңдеулерді жіктеу және канондық түрге келтіру.

3) Шешімдер түсінігі. Классикалық және жалпы.

Дәрістің қысқаша мазмұны:

Математикалық физика теңдеулеріне қойылатын есептер.

Математикалық физика теңдеулері - физиканы математика пәндерімен байланыстырады яғни физикалық процестерді математикалық анализ апаратымен зерттей отырып дифференциялдық теңдеулерді құрамыз

Математикалық физика есебі деп келесі екі шартты айтамыз

1. Теңдеу
2. Қосымша шарттар

Құрылған теңдеулер 2, 3 және n айнымалы функциядан және оның дербес туындыларынан құрылады.

Теңдеулер орындалу үшін қосымша шарттар қойылады, бастапқы және шектік шарттар.

Көп айнымалы функцияның теңдеуі келесі түрде болады.

F( $x_{1}, x_{2}. .$ , $x_{n}$ , t, u( $x_{1}, x_{2}. .$ , $x_{n}$ , ), $\frac{\partial^{k_{1} + k_{2} + k_{n}}}{\partial x_{1}\partial x_{2}\partial x_{n}}$ ) =0 (1)

n=2: F(x, y, t, u(x, y), u _t , u _x , u _y , u _tt, u _xx , u _yy ) =0 (2)

1. мен (2) ге қосымша шарттар қойылады.

1. Бастапқы шарт t=0, u(x, 0) =φ(x), ut(x, 0) =ψ(x) (3)
2. x=0, u(0, t) =φ(t), ux(0, t) =ψ(t)
3. x=l, u(l, t) =φ(t), ux(l, t) =ψ( (4)

1. мен (2) ге (3) пен (4) шарттары қойылса онда математикалық физиканың есебі құрылған дейміз.

Анықтама: Егер (1) мен (2) теңдеулер t уақыттан тәуелсіз болса, онда физикалық процесс стационарлық деп аталады.

Анықтама: Егер теңдеудің бастапқы шектік шарты берілсе, онда ол аралас есеп деп аталады.

Анықтама: Егер теңдеудің бастапқы шарты берілсе, онда ол есеп Коши есебі деп аталады.

Анықтама: Математикалық физика есебі дұрыс қойылған деп аталады, егер:

1. шешімі болса;
2. жалғыз шешім;
3. Шарттқа қатысты тұрақты шешім

Екінші ретті дербес туындылы теңдеулерді классификациялау және канондық түрге келтіру.

Классикалық және жалпылама шешім туралы түсінік.

Анықтама: Pz _x +Qz _y =0 (**), дифференциялды теңдеуі берілсін

$\frac{P}{\text{dx}} = \frac{Q}{\text{dy}}$ (*) .

Егер φ(x, y) =C (*) жалпы интегралы болса, z(x, y) = φ(x, y) (**) жалпы шешім болады.

Екінші дербес туындылы сызықты теңдеулер үш топқа бөлінеді:гиперболалық, параболалық, эллиптикалық.

Екінші ретті дербес туындылы теңдеуін келесі түрде жазайық.

Мұндағы A, B, C:

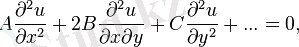
- коэффициенті. Бұл теңдеуді канондық түрге элементар түрлендірудің көмегімен келтірейік. $\text{Ady}^{2} - 2\text{Bdxdy} + \text{Cdx}^{{}^{2}} = 0$ . Бұл характеристикалық теңдеу деп аталады. Ол конустық қисықтың теңдеуіне ұқсас.

Конустық қисық тәрізді дискриминанттың таңбасына байланысты

( D=B ² -AC) эллипстерге, параболалар мен гиперболаларға бөлінеді.

1. Гиперболалық теңдеу,
2. - Эллиптикалық теңдеу,
3. - Параболалық теңдеу,

Бұл жерде берілген нүктеде A, B, C коэффициенттері бір мезетте нөлге айналмайды деп аламыз. Барлық A, B, C коэффициенттері тұрақты болған жағдайда теңдеудің x және y. Айнымалылар жазықтығының барлық нүктелерінде бір типті болады. A, B, C коэффициенттері x және y ке тәуілді болса, онда берілген теңдеу гиперболалық(эллипстік) жататын нүктелер жиыны жазықтықта гиперболалық (эллипстік) деп аталатын ашық облысты түзеді, ал теңдеуді параболалық типке жатқызатын нүктелер жиыны тұйық болады.

Өздік жұмыс тапсырмалары:

1. Математикалық физиканың толық қойылған есебі дегеніміз не?

2. Қандай құбылыс стационар құбылыс деп аталады?

3. Классикалық және жалпылама шешімдерге анықтама бер.

4. Коши есебіне анықтама беріңіз.

5. Дербес туындылы теңдеудің классификациясын ата.

Негізгі әдебиеттер: [1], [6]

Қосымша әдебиеттер: [1], [5], [6]

2. ГИПЕРБОЛАЛЫҚ ТИПТЕГІ ТЕҢДЕУ.

2 дәріс. Гиперболалық типтегі теңдеу. Коши есебі.

Дәрістің мақсаты: Гиперболалық типтегі теңдеулер ұғымын беру. Толқындық теңдеулер үшін Коши есебіе шешу және жалпы шешімді табу дағдыларын қалыптастыру.

Тақырыптың негізгі сұрақтары:

1) Гиперболалық типтегі теңдеулер

2) Коши есебі. Даламбер формуласы. .

3) Толқындық теңдеудің жалпы шешімі. .

Дәрістің қысқаша мазмұны:

Гиперболалық типтегі теңдеу. Жалпы шешім.

Әртүрлі тербелістермен байланысты есептер гиперболалық типті теңдеулерге әкеледі, шектің, мембрананың тербелісі, электромагниттік тербелістер т. б.

Шектің тербеліс теңдеуі: . $u_{\text{tt}} = a^{2}u_{\text{xx}} + f(x, y, t)$

Мембрананың тербеліс теңдеуі: $u_{\text{tt}} = a^{2}(u_{\text{xx}} + u_{\text{yy}}) + f(x, y, t)$

Дербес туындылардың теңдеулері үшін шешімнің жалпы түрін көрсету мүмкін емес, бірақ кейбір дербес жағдайларда оны табуға болады. Бұл жалпы шешімдер еркін тұрақтылардан емес, еркін функциялардан тәуелді. Осы функцияларды сәйкес анықтай отырып қандайда бір қосымша ашрттарды қанағаттандыруға болады. Шектің тербеліс теңдеуінің жалпы шешімін табуға мысал келтірейік: $u_{\text{tt}} = a^{2}u_{\text{xx}}$ (1)

Канондық түрге келтіреміз:

Характеристикалық теңдеу $\text{dx}^{2} - a^{2}\text{dt}^{2} = 0$ ал оның интегралы x-at=c ₁ , x+at=c ₂

Айнымалылар енгіземіз : ξ=x-at, η=x+at, және туындыларды табамыз $u_{x} = u_{\xi} + u_{\eta}$ , , $u_{t} = u_{\xi}( - a) + u_{\eta}a$ , $u_{\text{tt}} = u_{\text{ξξ}}a^{2} - 2u_{\text{ξη}}a^{2} + u_{\text{ηη}}a^{2}$

Бұл мәндерді (1) теңдеуге қойып $u_{\text{ξη}} = 0$ канондық теңдеуді аламыз. $u_{\eta} = v$ (2), ауыстыруын жасап $v_{\xi}(\xi, \eta) = 0$ . аламыз. Бұл теңдеуді ξ ден тәуелсіз кез келген функция қанағаттандырады, сәйкесінше v=f(η) (3), , мұндағы f(η) - η. еркін функциясы. (3) ті (2) ге қойсақ $u_{\eta}(\xi, \eta) = f(\eta)$ . (4) (4) интегралдау арқылы $u(\xi, \eta) = \int_{}^{}{f(\eta) }d\eta + f_{1}(\xi)$ ,, мұндағы f ₁ (ξ) - ξ. дің еркін функциясы. η, ның функциясын $\int_{}^{}{f(\eta) }d\eta = f_{2}(\eta)$ , деп белгілеп, : $u(\xi, \eta) = f_{1}(\xi) + f_{2}(\eta)$ алуға болады. Бұрынғы (x, t) айнымалыларға оралсақ келесі түсінікті аламыз. : $u(x, t) = f_{1}(x - \text{at}) + f_{2}(x + \text{at})$ (1) теңдеудің шешімі (5) функция екенін көруне болады. Егер f ₁ мен f ₂ екі рет үзіліссіз дифференциялданатын функциялар, (5) өрнегі (1) теңдеудің жалпы шешімі.

Коши есебі. Даламбер формуласы. .

Коши есебі келесідей қалыптасады. u(x, t) функциясын табу керек, үздіксіз $- \infty < x < \infty, t \geq 0$

$u_{\text{tt}} = a^{2}u_{\text{xx}} + f(x, y, t)$ теңдеуін қанағаттандыратындай $- \infty < x < \infty, t > 0$ бастапқы шарт u(x, 0) =φ(x), u _t (x, 0) =ψ(x), $- \infty < x < \infty$ (6) , мұнда φ(x), ψ(x) - берілген функция. Коши есебін $u_{\text{tt}} = a^{2}u_{\text{xx}}$ үшін қарастырамыз. Шешімі болады деп болжаймыз. Себебі функция u(x, t) (1), теңдеуді қанағаттандырады, яғни (5) түрде міндетті түрде болу керек. (6) теңдікті қанағаттандыратындай, f ₁ және f ₂ жалпы шешімін табу керек. (5) және (6) сәйкестендіре келе, алатынымыз: $f_{1}(x) + f_{2}(x) = \phi(x)$ , (7) $- \text{af}'_{1}(x) + \text{af}'_{2}(x) = \psi(x)$ (8) . 2- ші теңдеуді интегралдай келе, алатынымыз $f_{1}(x) - f_{2}(x) = - \frac{1}{a}\int_{0}^{x}{\psi(\alpha) d\alpha + c}$ (9) . (7), (9) дан алатынымыз

$f_{1}(x) = \frac{1}{2}\phi(x) - \frac{1}{2a}\int_{0}^{x}{\psi(\alpha) d\alpha + \frac{c}{2}}$ , $f_{2}(x) = \frac{1}{2}\phi(x) + \frac{1}{2a}\int_{0}^{x}{\psi(\alpha) d\alpha - \frac{c}{2}}$ (10), $- \infty < x < \infty$ . қатысты (10) сәйкестендіре, f ₁ және f ₂ (5) алатынымыз $u(x, t) = \frac{1}{2}\phi(x - \text{at}) - \frac{1}{2a}\int_{0}^{x - \text{at}}{\psi(\alpha) d\alpha + \frac{c}{2} + \frac{1}{2}\phi(x + \text{at}) + \frac{1}{2a}}\int_{0}^{x + \text{at}}{\psi(\alpha) d\alpha - \frac{c}{2}}$ әлде $u(x, t) = \frac{1}{2}\left\lbrack \phi(x - \text{at}) + \phi(x + \text{at}) \right\rbrack + \frac{1}{2a}\int_{x - \text{at}}^{x + \text{at}}{\psi(\alpha) d\alpha}$ (11) . . (11) . қатынас Даламбер формуласы деп аталады.

Өзін-өзі тексеру сұрақтары:

1. Қандай процесс гиперболалық типтегі теңдеуді сипаттайды?

2. Тербеліс теңдеуі мен мембрананың жалпы түрін жаз.

3. Тербеліс теңдеуінің жалпы шешімі қалай табылады?

4. Гиперболалық теңдеу үшін Коши есебін құрып, қолдану

5. Даламбер формуласын жаз.

Негізгі әдебиеттер: [1], [4]

Қосымша әдебиеттер: [1], [5], [6]

3 дәріс. Тербеліс теңдеуі үшін аралас есеп.

Дәрістің мақсаты: Шектің тербеліс теңдеулерінің шешімін табу үшін Фурье әдісін беру ( шешім көбейтінді түрінде табылады) Шектің тербеліс теңдеуі үшін аралас есепті шешу дағдыларын қалыптастыру.

Тақырыптың негізгі сұрақтары:

1) Есептің қойылуы.

2) Фурье әдісі

Дәрістің қысқаша мазмұны:

Есептің қойылуы.

Қатты бекітілген шек үшін бірінші бастапқы қайтарым және жылдамдық айтылады. Шектің тербеліс заңын табу керек.

$u_{\text{tt}} = a^{2}u_{\text{xx}}$ (1)

$u(0, t) = 0$ , $u(l, t) = 0$ (2)

$u(x, 0) = \phi(x)$ , $u_{t}(x, 0) = \psi(x)$ (3)

Фурье әдісімен шешу.

Аралас есеп Фурье әдісімен шешілед, яғни шешімін туынды ретінде табамыз. . $u(x, t) = X(x) \ast T(t)$ (4)

$$X(x) \ast T^{''}(t) = a^{2}X^{''}(x) \ast T(t)$$

$$\frac{T^{''}(t) }{a^{2}T(t) } = \frac{X^{''}(x) }{X(x) } = - \lambda$$

$$\begin{array}{r} \left\{ X^{''}(x) + \lambda X(x) = 0, ( \ast ) \middle \right. \ \end{array}$$

1. (*) табамыз.

$X^{''}(x) + \lambda X(x) = 0$ , X(0) =0, X(l) =0, u(x, t) =X(x) *T(t), u(0, t) =X(0) *T(t) =0.

Λ мағынасы меншікті мән, а теңдеудің шешімі-меншікті функция. (*) есебі шарттарымен Штурма-Лиувиль есебі деп аталады. Характеристикалық теңдеу құрайық.

k ² +λ=0, k ² =-λ

1. λ<0, k=±−λk = \pm \sqrt{- \lambda}және шешімі болады.

$$X(x) = C_{1}e^{\sqrt{- \lambda}x} + C_{2}e^{- \sqrt{- \lambda}x}$$

X(0) =C ₁ +C ₂ =0 => C ₁ =-C ₂

2. λ=0, k=0, X(x) =C1+C2x

$\begin{array}{r} \left\{ X(0) = C_{1} = 0, \middle \right. \ \end{array}$ Бұл 3 жағдай

3. λ>0\lambda > 0, k=±iλk = \pm i\sqrt{\lambda}

$$X(x) = C_{1}\text{cos}\sqrt{\lambda}x \pm C_{2}\text{sin}\sqrt{\lambda}x$$

$$X(0) = C_{1} = 0, \text{=>}C_{1} = 0$$

$X(l) = C_{1}\text{cos}\sqrt{\lambda}l + C_{2}\text{sin}\sqrt{\lambda}l = C_{2}\text{sin}\sqrt{\lambda}l = 0$ , C ₂ ≠0, C ₂ =1.

$\text{sin}\sqrt{\lambda}l = 0$ , $\sqrt{\lambda_{n}}l = \pi n$ ,

$\lambda_{n} = (\frac{\pi n}{l}) ^{2}$ - Меншікті мәндер функциясы.

$X_{n}(x) = \text{sin}\frac{\pi n}{l}x$ - Меншікті функциялар

Енді (**) шешеміз.

$T^{''}(t) + {\lambda a}^{2}T(t) = 0$ ,

$$T^{''}(t) + (\frac{\pi\text{na}}{l}) ^{2}T(t) = 0$$

$\lambda > 0$ => $T_{n}(t) = A_{n}\text{cos}\sqrt{\lambda_{n}}\text{at} + B_{n}\text{sin}\sqrt{\lambda_{n}}\text{at}$ ,

$T_{n}(t) = A_{n}\text{cos}\frac{\pi\text{na}}{l}t + B_{n}\text{sin}\frac{\pi\text{na}}{l}t$ .

(4) сәйкестендіре алатынымыз

$u_{n}(x, t) = \sum_{n = 1}^{\infty}{(A_{n}\text{cos}\frac{\pi\text{na}}{l}t + B_{n}\text{sin}\frac{\pi\text{na}}{l}t) \text{sin}n\frac{\pi n}{l}x}$ . (5)

(2) және(3) шарттарға сәйкес A _n және B _n коэффициенттерін (5) ке қойып есептейміз. φ(x), ψ(x) функциясы беттеседі, сондай-ақ Фурье қатарынан sin бойынша алатынымыз

$A_{n} = \frac{2}{l}\int_{0}^{l}{\phi(x) \text{sin}\frac{\pi n}{l}\text{xdx}}$ (6), $B_{n} = \frac{2}{\pi\text{na}}\int_{0}^{l}{\psi(x) \text{sin}\frac{\pi n}{l}\text{xdx}}$ (7) . (6) және (7) ні (5) ке қойып,

(1), (2), (3) . -тің жалпы шешімін табамыз. Содан шешімі бар, ол жалғыз және тұрақты шартқа қатысты.

Өзін-өзі тексеру сұрақтары:

1. Сформулируйте постановку смешанной задачи колебания струны.

2. Фурье әдісі немен қорытындыланады?

... жалғасы

Математикалық физика теңдеулері және оларды канондық түрге келтіру

Эйнштейн теңдеулері

Максвелл теңдеулері

Математикалық физиканың дифференциалдық теңдеулерінің негізгі түрлері

Шаңкөмірлі отынды жағу кезіндегі жану камерасының температуралық сипаттамаларына ауырлық күшінің әсері

Бессель теңдеуінің шешімі

Лаплас теңдеуі үшін шеттік есептер

Электростатиканың есептері

ШЕКТЕЛГЕН СТЕРЖЕНЬДЕГІ ЖЫЛУ ӨТКІЗГІШТІК ТЕҢДЕУІНІҢ ҚОРЫТЫНДЫЛАУ ЖӘНЕ ОНЫ ФУРЬЕ ӘДІСІМЕН ИНТЕГРАЛДАУ

Спиндік жүйелердің теориясы

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс