Тригонометриялық және периодты функциялардың қасиеттері, анықталу облысы, мәндер жиыны мен кері функциялары

Сабақтың тақырыбы: Тригонометриялық және периодты функциялар, олардың қасиеттері. Анықталу облысы, мәндерінің жиыны. Кері тригонометриялық функциялар. Тригонометриялық функциялардың графиктері.

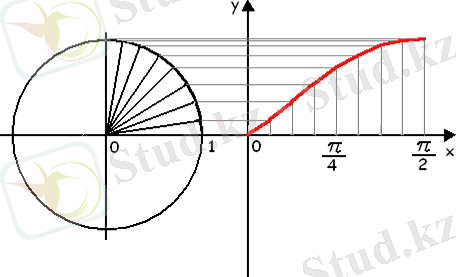
у = sin х .

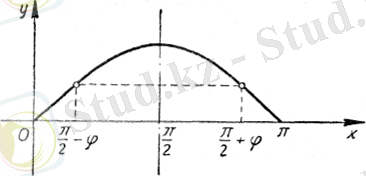
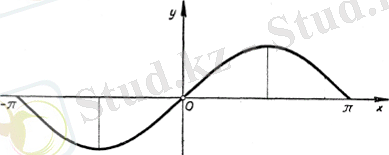
Функцияның тақтығы Функцияның периодтылығы

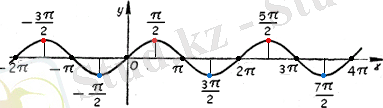
Синусоида қисығы

Қасиеттері

1. Функцияның анықталу облысы х€R.
2. Мәндер жиыны [-1; 1]
3. sin(x+2π) =sinx, функция периодты, себебі оның ең кіші периоды 2π.
4. Функция тақ, sin(-x) =-sinx
5. [-π/2+2πk; π/2+2πk] кесінділерінде бір сарынды өспелі
6. [π/2+2πk; 3π/2+2πk] кесінділерінде бір сарынды кемімелі

У=sinx функциясының графигін синусоида қысығы деп атайды.

2. y= cos x функциясын cos х = sin ( х + ^π / ₂ ) .

1. Функцияның анықталу облысы х€R.

2. Мәндер жиыны [-1; 1]

3. cos(x+2π) =cosx, функция периодты, себебі оның ең кіші периоды 2π.

4. Функция жұп, cos (-x) =cosx

5. [-π+2πk; 2πk] кесінділерінде бір сарынды өспелі

[2πk; π+2πk] кесінділерінде бірсарынды кемімелі

У=cosx функциясының графигін косинусоида қысығы деп атайды

Тангенс функциясы

:

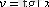
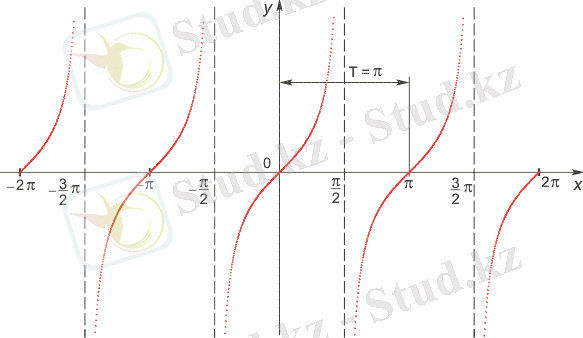
Мәндер жиыны - барлық нақты сандар жиыны, яғни тангенс - шексіз функция .

Функция тақ: tg(−x) =−tg x Графигі бас нүктеге қарағанда симметриялы қисық.

Функция периодты: Ең кіші оң периоды π, яғни tg(x+π· k ) = tg x, k ∈ Z

:

:

:

:

:

:

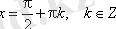Анықталу облысы - жиынынан басқа барлық нақты сандар жиыны

tg x = 0 егер

tg x > 0 барлық

tg x < 0 барлық

Функция бірсарынды өспелі :

:

:

:

:

:

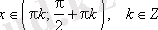
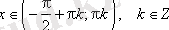
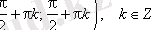
Котангенс функциясы

:

Мәндер жиыны - Барлық нақты сандар жиыны, яғни котангенс - шексіз функция

Функция тақ : ctg(−x) =−ctg x . Графигі бас нүктеге қарағанда симметриялы .

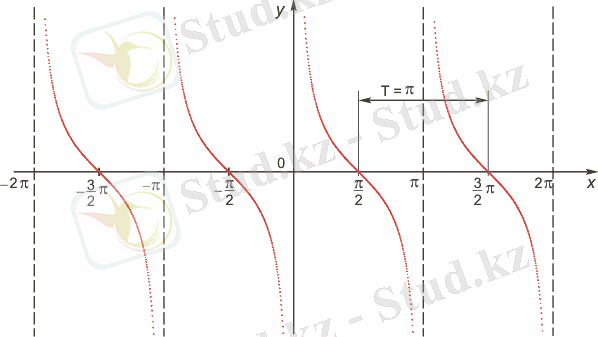
Функция периодты : ең кіші оң периоды π, яғни ctg(x+π· k ) =ctg x, k ∈ Z

:

:

:

:

:

:

Анықталу облысы - жиынынан басқа барлық нақты сандар жиыны

ctg x = 0 егер

ctg x > 0 барлық

ctg x < 0 барлық

Функция бірсарынды кемімелі

:

:

:

:

:

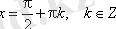
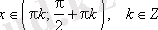
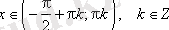
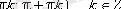
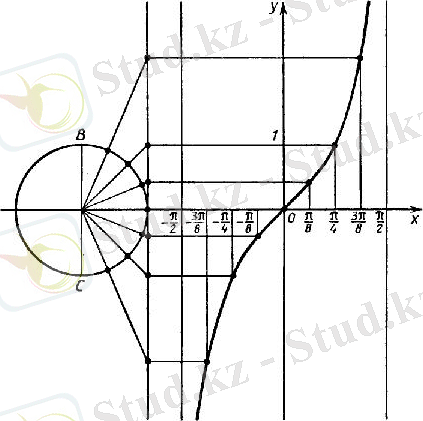
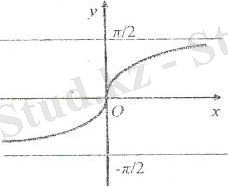
Тангенс пен котангенс функцияларының графиктері.

(-π/2; π/2) интервалында тангенс функцияның графигінің салынуы синус функциясының графигінің салынуымен бірдей.

Кері тригонометриялық функциялар

а) 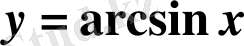функциясының кері функциясын қарастырайық.

- анықталу облысы:

- өзгеру облысы:

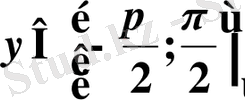
- Функция тақ, периодты емес, шектелген

- графигі Ох және Оу осьтерін координаталар бас нүктесінде қияды

- Функция анықталу облысында өседі

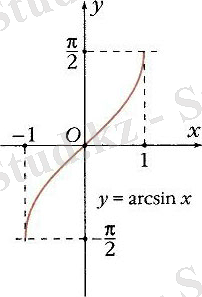
ә) 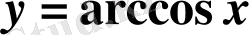функциясының кері функциясын қарастырайық.

- анықталу облысы:

- өзгеру облысы:

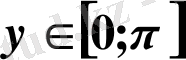
- Функция тақ емес, жұп та емес; периодты емес; шектелген.

- графигі Ох осін х=1 нүктесінде және Оу осін 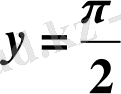нүктесінде қияды

- Функция анықталу облысы кемиді.

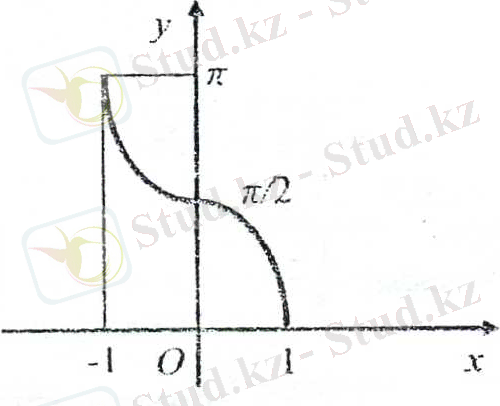
б) 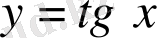функциясының кері функциясын қарастырайық.

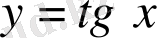функциясы 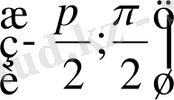интервалында

анықталған, бірсарынды өспелі және

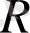
жиынындағы өзінің барлық мәндерін

қабылдайды. Демек 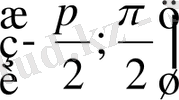интервалында

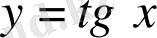функциясына кері функция

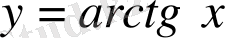болады. 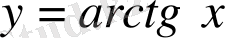функциясы

жиынында анықталған,

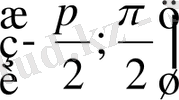
интервалында өзгеретін бірсарынды өспелі функция.

Енді 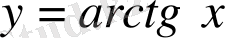функциясының қасиеттерін келтірейік:

1. функцияның анықталу облысы - барлық нақты сандар жиыны, ;

2) мәндер жиыны 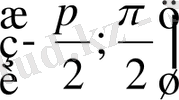интервалы;

3) функция тақ, кез келге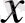н үшін ;

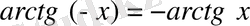4) функция бір сарынды өспелі.

Кез келге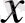н үшін 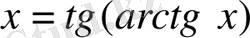тепе-теңдігі орындалады, мұндағы 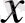үшін

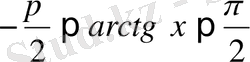
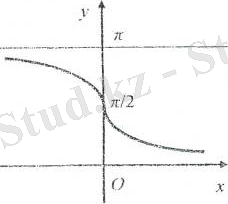
в) 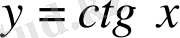функциясына кері функцияны

анықтайық:

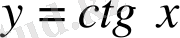функциясы 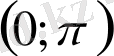интервалында

анықталған, бірсарынды кемімелі және сол

аралықта 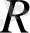жиынындағы өзінің барлық

мәндерін қабылдайды. Осы интервалда

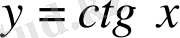функциясына

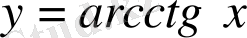
функциясы кері функция болып табылады.

Онда 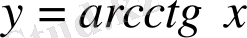функциясы

жиынында анықталған, 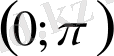интервалында өзгеретін бірсарынды кемімелі функция.

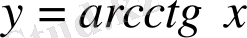функциясының қасиеттері.

1) анықталу облысы - барлық нақты сандар жиыны,

2) мәндер жиыны - 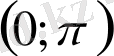аралығы;

3) функция жұп та тақ та емес;

4) функция бірсарынды кемімелі.

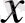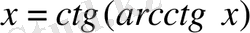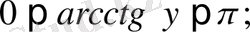
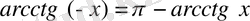Кез келген үшін , тепе-теңдігі орындалады.

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс