Дифференциалдық теңдеу. Шешім. Бағыттар өрісі. Интегралдық, фазалық қисықтар

Жұмыс түрі: Іс-тәжірибеден есеп беру
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

1-Лекция

Дифференциалдық теңдеу. Шешім. Бағыттар өрісі. Интегралдық, фазалық қисықтар. Дифференциалдық теңдеулерге келтірілетін есептер. Коши есебі. Шеттік есепртер. .

1. Негізгі ұғымдар. Дифференциалдық теңдеу деп әдетте тәуелсіз айнымалыны, ізделінетін функцияны және оның әр түрлі реттегі туындыларын (дифференциалдарын) байланыстыратын теңдеуді айтады.

Теңдеуге кіретін туындының (дифференциалдың) ең жоғарғы реті дифференциалдық теңдеудің реті деп аталады.

Егер ізделінетін функция тек бір аргументтен тәуелді болса, онда дифференциалдық теңдеу жай деп, ал бірнеше аргументтен тәуелді болса дербес туындылы дифференциалдық теңдеу деп аталынады.

Айтылғанға сай n-ші ретті жай дифференциалдық теңдеу жалпы түрде былай жазылады:

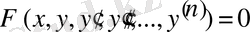. ( 1)

Мұндағы х-тәуелсіз айнымалы, у-ізделінетін функция, ал туындылар.

Егер (1) теңдеуде екі тәуелсіз айнымалы х ₁ , х ₂ , бір ғана ізделінетін функция 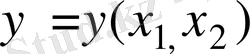болса, онда ол n-ші ретті дербес туындылы дифференциалдық теңдеу болар еді де, былай жазылар еді:

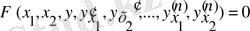Егер (1) теңдеуде n=1болса, онда алынған теңдеу

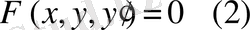
бірінші ретті дифференциалдық теңдеу деп, ал қалған 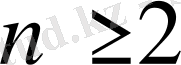болған

жағдайларда жоғары ретті дифференциалдық теңдеу деп аталады.

Егер (2) теңдеу бойынша шешілетін болса, онда алынған теңдеу.

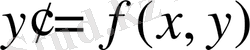(3)

туындысы бойынша (туынды қатысты) шешілген бірінші ретті дифференциалдық теңдеу деп аталады. (3) теңдеудегі 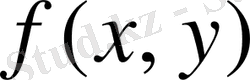фуекциясын кейінде берілген Д обылсында бір мәнді, қос аргумент бойынша үздіксіз деп есептейміз. Д - облысы (3) теңдеудің анықталу облысы деп аталады. Егер 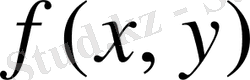функциясы қандайда болмасын бір 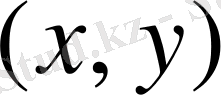нүктесінің аймағында ақырсыздыққа (шексіздікке) айналса, онда

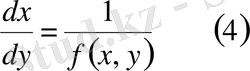
теңдеуі қарастырылады. 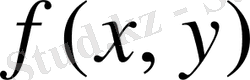функциясының осындай нүктелері мен оның анықталмаған, бірақ үздіксіздік қасиеті бойынша анықталуға келетін нүктелерінің жиынын да (3) теңдеудің анықталу обылысына жатқызамыз.

Айта кететін жай (4) теңдеуді, оны (3) теңдеуге қарағанда шешу оңай болатын жағдайларда да қарастырады.

Дифференциал теңдеудің шешімі деп, теңдеудегі белгісіз функцияның орнына қойғанда оны теңбе-теңдікке айналдырытын дифференциалданатын 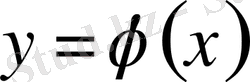функциясын айтады, яғни

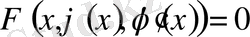Дифференциалдық теңдеудің шешімін табу процесі оны интегралдау деп аталады. Бұл интегралдау ұғымын анықталмаған интеграл алу (интегралдау) ұғымымен шатастырмас үшін, көбінесе соңғысын квадратуралау деп атайды. Осыған орай, дифференциалдық теңдеуді интеграл алу операциясына әкеп тіреу, оны квадратурада шешу (интегралдау) деп аталады.

Көп жағдайларда дифференциалдық теңдеудің шешімі айқындалмаған түрде табылады. (3) теңдеудің шешімі болатын функциясын айқындалмаған түрде анықтайтын арқылы

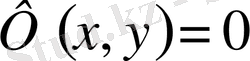(5)

өрнегі (3) теңдеудің айқындалмаған түрдегі шешімі деп аталады.

Жалпы алғанда дифференциалдық теңдеудің шешімдері шексіз жиын құрайды. Себебі дифференциалдық теңдеуде міндетті түрде ізделінетін функцияның туындылары немесе дифференциалдары бар. Және де дифференциалдық теңдеуді интергалдау, жалпы айтқанда, түбінде алғашқы образды табуға әкеп соғады. Ал алғашқы образ, бұрынан белгілі, кез келген тұрақты қосылғышқа дейінгі дәлдікпен табылады.

Мысалға бірінші ретті туындысы бойынша шешілген дифференциалдық теңдеу қарастырайық

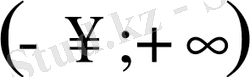аралығында бұл теңдеудің барлық шешімдері мына функциямен анықталатынын оңай көруге болады. Мұндағы тұрақты С кез-келген сандық мәнге ие бола алады. С-ға кезкелген сандық мәндер беріп, шешімдердің шексіз жиынын алуға болады.

Әйткенмен көбінесе теориялық немесе практикалық есептерді шешкенде теңдеудің барлық шешімдерін табу емес, қосымша бір шарттары қанағаттандыратын шешім табу талап етіледі. Осындай есептің біреуі -дифференциалдық теңдеулер теориясында елулі маңыз атқаратын - Коши есебі.

(3) теңдеу үшін Коши есебі былай қойылады. (3) теңдеудің барлық 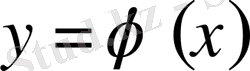шешімдерінің ішінен болғанда берілетін мән 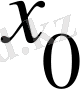-ді қабылдайтын, яғни 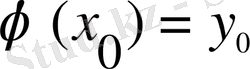шартын қанағаттандыратын 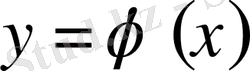шешімін табу керек. Қысқаша Коши есебі былай жазылады:

y′=f (x, y), y (x ₀ ) =у _0.

Берілген х ₀ , y ₀ - сандары бастапқы мәндер немесе бастапқы берілгендер деп, ал 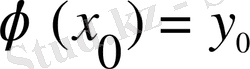шарт 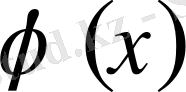-шешімнің бастапқы шарты деп аталады.

Мысалға y′ =cosx теңдеуді қарастырайық. Теңдеудің барлық шешімдерінің ішінен 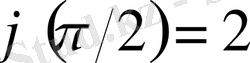бастапқы шартын қанағаттындыратын шешімді табайық. Бастапқы 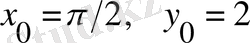мәндеріне сәйкес бұл шешім С-ның белгілі бір мәнінде табылады. Ол үшін табылған y = sinx +С шешімдер жиынын 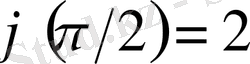бастапқы шартқа қоялық: 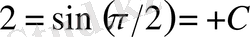. Бұдан С=1. Сонымен іздеп отырған шешіміз

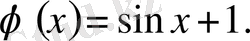
Дифференциалдық теңдеудің айқындалған немесе айқындалмаған түрдегі шешімі: 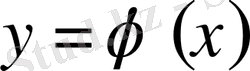, ф(х, y) =0 геометриялық тұрғыдан қарағанда - сызық. Бұл сызық (3) теңдеудің интегралдық қисығы деп аталады. (3) теңдеу үшін қойылған Коши есебіне мынадай геометриялық түсініктеме беруге болады:

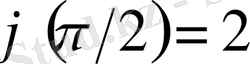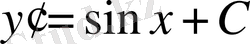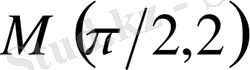
(3) теңдеудің барлық интегралдық қисықтарының ішінен берілген М ( х ₀ , y ₀ ) нүктесі арқылы өтетін қисықты табу керек. Қарастырылған Коши есебінің мәні формуламен берілген барлық синусоидалардың ішінен 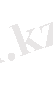нүктесі арқылы өтетін синусоиданы табу.

Коши есебінің жалғыз ғана шешімі өтетін нүкте жалғыздық нүктесі деп, ал осы нүтеден жалғыз ғана шешім өтетіндік шарты-жалғыздық шарты деп аталады.

Жоғарыда айтылғандай, дифференциалдық теңдеуді интегралдау нәтижесінде кез келген тұрақтылардан тәуелді функция аламыз. Мысалға бірінші ретті дифференциалдық теңдеуді интегралдағанда х-дан басқа кез келген тұрақты С-дан тәуелді функция

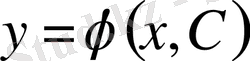(6)

яғни, іс жүзінде, шешімдер тобын аламыз. Мұндай шешімдер тобын әдетте жалпы шешім деп атайды. (6) формуладан, жалпы айтқанда, кез келген Коши есебінің шешімін таба аламыз. Ол үшін бастапқы мәндерге сәйкес келетін С-ның мәнін табу керек. Әрине бұл үшін (6) өрнек Сбойынша шешілуі қажет және бастапқы мәндерге сәйкес келетін шешімнің жалғыз болуы шарт. Осы мақсатпен жалпы шешімнің төмендегідей анықтамасы қабылданған.

Айталық Д- (х, у) жазықтығында жататын, кез келген нүктесі жалғыздық нүкте болатын облыс болсын.

Егер:

1) 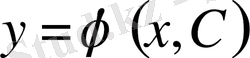өрнек Д облысының кез келген (х, у) нүктесінде С бойынша шешілетін болса:

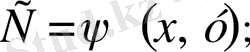
2) Д облысының кез келген (х, у) нүктесі үшін 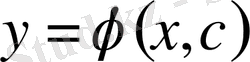формуладан табылған С-ның -ті қоса қарастырғандағы мәндерінде (6) функция (3) теңдеудің шешімі болатын болса; онда х, С шамаларының өзгеру облысында анықталған 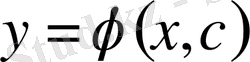функциясын (3) теңдеудің жалпы шешімі деп атайды.

Бұл анықтамадан мынау көрініп тұр: егер жалпы шешім белгілі болса, онда Д облысынан алынған кез келген бастапқы мәндер үшін, осы мәндермен анықталатын Коши есебінің шешімін табуға болады. Шынында да 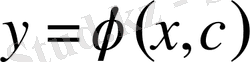жалпы шешімді бастапқы 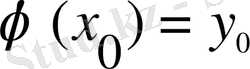шартына қоялық. Онда .

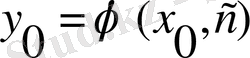Жалпы шешімнің анықтамасы бойынша бұл өрнек С бойынша шешіледі:

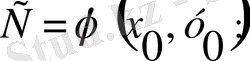
Осы табылған мәнді мәнді (6) формулаға апарып қоялық. Сонда бастапқы шартты қанағаттандыратын 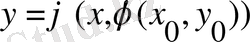шешімін аламыз.

Кез келген нүктесінде жалғыздық шарты орындалатын шешім дара ( жеке, дербес) шешім деп аталады.

Жалпы шешімнің анықтамасынан тұрақты С-ның -ті қоса қарастырғандағы белгілі бір мәнінде жалпы шешімнен алынатын шешім, дара шешім болатыны шығады.

Кез келген нүктесінде жалғыздық шарты бұзылатын (орындалмайтын) шешім ерекше шешім деп аталады.

Ерекше шешімге сәйкес келетін интергралдық қисық жалпы шешім құрайтын қисықтар тобына жатпайды. Сондықтан ерекше шешім жалпы шешім анықталған Д облысында жатпайды. Ерекше шешім, әрине, тұрақты С-ның -ті қоса санағандағы кез келген мәндерінде жалпы шешімнің формуласынан табылмайды. Егер дифференциалдық теңдеуді интегралдағанда жалпы шешім айқындалмаған түрде алынбайтын болса, онда оны әдетте жалпы интеграл деп атайды. 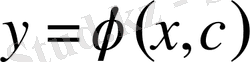Д облысында жалпы шешім болатын функциясын айқындалмаған түрде анықтайтын Ф(х, y, с) =0 өрнегін (3) теңдеудің Д облысындағы жалпы интегралы деп атайды.

Егер (3) теңдеудің жалпы интегралы Ф ₀ (х, y) = С түрінде жазылса, онда Ф ₀ (х, y) функциясы (3) теңдеудің интегралы деп аталады.

Мысал. 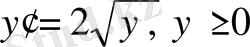теңдеудің шешімдерін табу керек.

Шешуі. 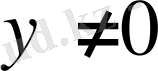деп алып, берілген теңдеуді мына түрде 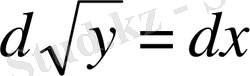жазайық.

Бұдан 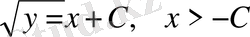, себебі y>0, немесе .

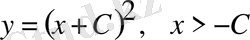Бұл берілген теңдеудің жалпы шешімі. Оған y = 0 мәні кірмейді. Егер

y = 0 мәнін қарастырсақ, оның теңдеудің шешімі болтындығы көзбе - көз көрініп тұр. Бұл шешімнің (х-өсінің ) кез келген нуктесінен екі шешім өтіп тұр: біреуі жалпы шешімнен С-ның осы нүктеде анықталатын мәніне сәйкес алынатын парабеланың бір бұтағы, ал екіншісі осы y = 0 түзуінің өзі:

Олай y = 0 ерекше шешім.

Коши теоремасы. Егер 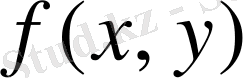функциясы мен оның дербес туындысы 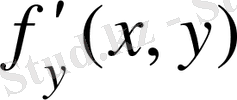Оxy жазықтығының белгілі бір облысында анықталған және үзіліссіз болса, онда бұл облыстың қандай да бір ішкі нүктесі 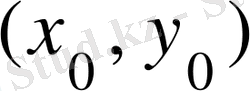-дің кейбір төңірегінде (3) теңдеудің 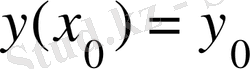бастапқы шартты қанағаттандыратын жалғыз шешімі бар болады.

Бұл теорема (3) теңдеуі берілсе, оның шешімі бар және ол жалғыз ғана болатынын білу мүмкіндігін көрсетеді. Теореманың геометриялық мағынасы: D облысының әрбір ішкі нүктесі арқылы жалғыз ғана интегралдық қисық өтеді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.