Физика. Механика

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 30 бет
Таңдаулыға:

Кіріспе
Механика - материалдық денелердің қозғалысын және олардың өзара әсерлесуін зерттейтін ғылым. Механикалық қозғалыс деп уақыт өзгеруіне сай денелердің кеңістіктегі орын ауыстыруын айтады. Денелердің өзара механикалық әсерлесуінің өлшеуіші ретінде алынатын шаманы күш дейді.
Теориялық механикада қарастырылатын заңдар, теоремалар, қағидалар механикалық қозғалыстың жалпы заңдылықтарын қамтиды. Себебі оларды дәлелдегенде денелердің тек негізгі механикалық қасиеттері қарастырылады. Теориялық механикада алынған заңдар мен қағидалар деформацияланатын денелердің механикасында (серпімділік теориясы, пластикалық теориясы, ағымдылық теориясы, қирау теориясы, гидромеханика, газдар динамикасы) қолданылады. Сондықтан, теориялық механика жалпы механиканың, сондай-ақ көптеген инженерлік пәндердің негізін құрайды.
Теориялық механика үш бөлімнен тұрады: статика, кинематика, динамика.
Статика тыныштықта болу, бір орында тұру, қозғалмау деген ұғымды білдіретін гректің Status сөзінен алынған. Статика - күштер мен күштер жиынтығын қарапайым түрге келтіретін теориялық механиканың бөлімі. Сондай-ақ статикада күштер жүйесінің әсеріндегі материалдық денелердің тепе теңдік шарттары алынады. Бұдан былай материалдық дененің тепе теңдігі деп оның тыныштық күйін айтатын боламыз.
Кинематика қозғалыста болу деген ұғымды білдіретін гректің kinema сөзінен шыққан. Кинематика материалдық дене қозғалысын геометриялық тұрғыдан зерттейді. Сондықтан кинематиканы кейде уақыт ұғымы бар қозғалыс геометриясы деп те атайды. Кинематикалық сипаттамаларға траектория, жүріп өткен жол, қозғалыстың жылдамдығы мен үдеуі жатады.
Динамика сөзі күш деген ұғымды білдіретін гректің dinamicos сөзінен шыққан. Динамика күш әсеріндегі материалдық денелердің қозғалысын зерттейді. Динамикада материалдық денелерге түсірілген күштер тепе теңдікте болмайды. Мәселе әсер етуші күштер мен дене қозғалысының арасындағы байланысты зерттеуде, қозғалыстың жалпы заңдарын орнатуда.
Бұл мәселені шешу үшін барлық материалдық денелерді ойша көлемін ескермеуге болатын материялық нүктелерге бөлшектейміз. Яғни, барлық денелерді материялық нүктелердің жиынтығы мен жүйесі деп қарастырамыз. Алдымен жеке бір материялық нүкте қозғалысының заңдарын зерттейміз. Одан кейін алынған нәтижелерді бірнеше материялық нүктеге немесе механикалық жүйеге қолданамыз. Осы жолмен кез келген материалдық дене қозғалысының жалпы заңдарына келеміз.
Динамика екі бөлімнен тұрады: материялық нүкте динамикасы және механикалық жүйе динамикасы. Механикалық жүйе динамикасында материалдық денелер қозғалысының жалпы заңдары алынады. Материялық нүкте динамикасын механикалық жүйе динамикасына кіріспе ретінде қарастыруға болады, алайда оны жеке де қарастыруға болады.
1 СТАТИКА
Күш ұғымы статиканың негізгі ұғымдарының бірі. Механикада қарастырылатын шамалар скалярлық және векторлық шамалар болып бөлінеді. Скалярлық шамалар деп тек сандық мәнімен ғана толық сипатталатын шамаларды айтамыз. Векторлық шамалар деп сандық мәнімен қатар бағытымен де сипатталатын шамаларды айтамыз.
Денелердің өзара әсерлесуінің өлшеуішін сипаттайтын шама күшдеп аталады. Күш - векторлық шама. Күштің денеге әсері а) күштің сандық мәнімен (модулімен), ә) күштің бағытымен, б) күштің түсу нүктесімен анықталады. Күш алынған масштабта ұзындығы күштің шамасын анықтайтын векторымен бейнеленеді, вектордың басы күштің түсу нүктесімен дәл келеді (А нүктесі), вектордың бағыты күш бағытын анықтайды. Бойымен күш векторы бағытталған KL түзуі күштің әсер ету сызығы деп аталады (1.1 а) сурет).

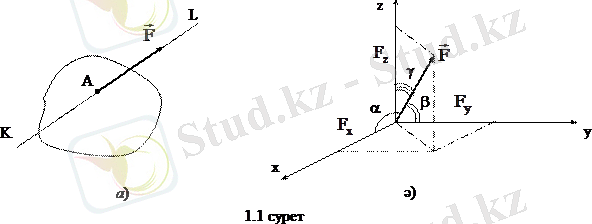
Күшті аналитикалық түрде оның координата өстеріне проекциялары арқылы анықтауға болады (1.1 ә) сурет). Бұл жағдайда күш шамасы мына өрнекпен анықталады:
, (1.1.1)
ал күш бағыты бағыттаушы косинустармен анықталады:
. (1.1.2)
Бір денеге әсер ететін ( ) күштер жиынтығы күштер жүйесі деп аталады. Егер дененің күйін өзгертпей оған әсер ететін ( ) күштер жүйесін басқа бір ( ) күштер жүйесімен алмастыруға болатын болса, мұндай екі жүйе пара-пар жүйелер деп аталады:
( )∾( ).
Егер дененің күйін өзгертпей оған әсер ететін ( ) күштер жүйесін бір күшпен алмастыруға болатын болса, онда бұл күш тең әсерлі күш деп аталады:
( )∾ .
Егер дене күштер жүйесінің әсерінен тепе-теңдікте болса, мұндай жүйе теңестірілгеннемесе нөлге пара-пар жүйе деп аталады:
( ) ∾ 0.
Статиканың аксиомалары
1 - аксиома (екі күштің тепе-теңдігі туралы аксиома). Екі күш әсер ететін қатты дене тепе-теңдікте болу үшін олардың модульдері тең болып, бір түзудің бойымен қарама-қарсы бағытталуы қажет және жеткілікті (1.2 сурет). Демек,
.
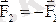
2 - аксиома. Қатты денеге әсер ететін кез келген күштер жүйесіне нөлге пара-пар күштер жүйесін қосқаннан немесе алып тастағаннан алғашқы күштер жүйесінің әсері өзгермейді.

1 және 2 аксиомалардың салдары.Күшті өзінің әсер ету сызығының бойымен кез келген нүктеге көшіруге болады, одан күштің денеге әсері өзгермейді.
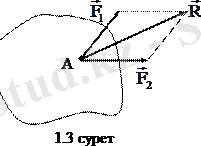
3 - аксиома (күштер параллелограмы туралы аксиома). Қатты дененің бір нүктесіне түскен екі күшті осы күштердің геометриялық қосындысына тең және сол нүктеге түскен тең әсерлі күшпен алмастыруға болады. Тең әсерлі күш аталған күштерден тұрғызылған параллелограмм диагоналімен анықталады (1.3 сурет):
.
Тең әсерлі күштің модулі:
.
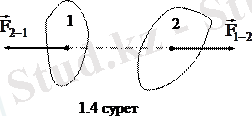
4 - аксиома. Екі дене бір-біріне әрқашан сан мәндері тең, бір түзудің бойымен қарама-қарсы бағытталған күштермен әсер етеді (1.4 сурет).
.

5 - аксиома (қатаю аксиомасы). Күштер жүйесі әсер ететін кез келген деформацияланатын денені тепе-теңдіктегі абсолют қатты дене ретінде қарастыруға болады.

Байланыстар және олардың реакциялары
Қозғалыс еркіндігі басқа денелермен шектелмеген дене еркін дене деп, ал шектелген дене еркін емес дене деп аталады. Берілген дененің қозғалысын шектеп, онымен жанасатын дене байланыс деп аталады. Берілген дене байланысқа бір күшпен әсер етеді. Бұл күшті қысым күші деп атайды. Байланыс та берілген денеге бір күшпен әсер етіп, оның қозғалысын шектейді. Бұл күш байланыс күші (реакция күші) немесе байланыс реакциясы деп аталады. Төртінші аксиомаға сәйкес қысым күші мен реакция күшінің шамалары тең және бір түзудің бойымен қарама қарсы бағытталады. Реакция күштерінің мәндері денеге әсер ететін актив (белгілі) күштерге тәуелді және белгісіз болады. Реакция күштері дененің мүмкін қозғалысына қарсы бағытталады. Байланыс дене қозғалысын бірнеше бағытта шектейтін жағдайда реакция күшінің бағыты белгісіз болады. Кейбір байланыстардың реакция күштерінің бағыттарын актив күштерге тәуелсіз көрсетуге болады. Осындай байланыстарды қарастырайық.
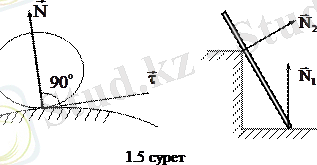
1. Қозғалмайтын жылтыр бет (жазықтық).Үйкелісін елемеуге болатын бетті жылтыр бет дейміз. Егер дене жылтыр беттің үстінде жатса,мұндай байланыстың реакциясы жанасу нүктесіне түсіп, жанасушы беттерге ортақ нормаль бойымен бағытталады ( - нормаль реакция, 1.5 сурет).
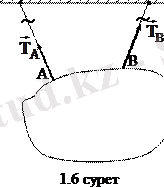
2. Созылмайтын иілгіш байланыс(жіп, арқан, сым арқан, шынжыр және т.б.). Реакциясы байланыстың бойымен оның іліну нүктесіне қарай бағытталады ( - керілу күші, 1.6 сурет).

3. Салмақсыз жіңішке сырық.Оның реакциясы сырықтың денемен бекітілу нүктесіне түседі де, егер сырық түзу сызықты болса оның бойымен, ал егер ол қисық сызықты болса оның басы мен ұшын қосатын түзудің бойымен бағытталады. Сырықтың өзі сығылуы немесе созылуы мүмкін ( - АВ сырығының реакциясы, 1.7 а) суреттегі сырық сығылады, 1.7 ә) суреттегі сырық созылады).
Жылжымайтын цилиндрлік топса (тірек) - мұндай байланыс қатты денеге топса өсіне перпендикуляр жазықтықта айналуға мүмкіндік береді. Бірақ бекітулі нүкте топса өсіне перпендикуляр жазықтықта қозғала алмайды, сондықтан реакция күші осы жазықтықта жатады және әсер ететін актив күштердің әсерінен кез келген бағытта болуы мүмкін. Демек байланыс реакциясы x және y өстерімен бағытталған екі құраушыға жіктеледі.
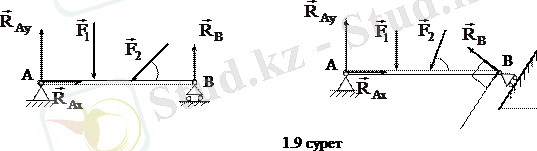
1.8 суретте және күштері әсер ететін, А ұшы топсалы тірекпен бекітілген, ал В ұшы жылтыр бетке сүйенген арқалық келтірілген. Жылжымайтын топсаның реакциясы және екі құраушыға жіктеледі, ал жылтыр беттің реакциясы бетке нормаль бойымен бағытталады.
5. Жылжымалы цилиндрлік топса (тірек) - реакциясытопса өсіне перпендикуляр жазықтықта жатады және тірек жазықтығына перпендикуляр бағытталады.( - жылжымалы топсаның реакциясы, 1.9 сурет).

6. Сфералық топса.Мұндай топса дененің бір нүктесін қозғалтпайды, бірақ дене сол нүктені айнала алады. Сфералық топсаның(1.10 а) сурет) реакциясы кеңістікте кез келген бағытта болуы мүмкін, сондықтан ол x, y және z өстерімен бағытталған үш құраушыға жіктеледі ( - сфералық топса реакцияларының құраушылары, 1.10 ә) және б) суреттер).
Есеп шығарған кезде келесі аксиоманы қолданады.
6 аксиома(байланыстардан арылу аксиомасы). Кез келген еркін емес денені еркін дене деп қарастыруға болады. Ол үшін дене қозғалысын шектейтін байланыстарды ойша алып тастап, олардың әсерін реакция күштерімен алмастыру керек.
Өзіндік бақылау сұрақтары:
1. Теориялық механика пәні нені зерттейді.
2. Күштің, күштер жүйесінің, пара-пар жүйелердің, тең әсерлі күштің, теңестірілген күштер жүйесінің ұғымы.
3. Статиканың аксиомалары.
4. Байланыс пен байланыс реакциясының анықтамасы.
5. Байланыстардың негізгі түрлері және олардың реакциялары.

Жинақталатын күштер жүйесінің тең әсерлі күші
⇐ Предыдущая12345678910Следующая ⇒

Абсолют қатты денеге әсер ететін күш жылжымалы вектор болғандықтан, жинақталатын күштер жүйесі бір нүктеге түсірілген күштер жүйесіне пара-пар (1.11 ә) суреттегі О нүктесі).
Теорема.Жинақталатын күштер жүйесін осы күштердің геометриялық қосындысына тең және олардың әсер ету сызықтарының қиылысу нүктесіне түсірілген тең әсерлі күшпен алмастыруға болады.
Дәлелдеу. Әсер ету сызықтары О нүктесінде қиылысатын жинақталатын күштер жүйесін (1.11 а) сурет) қарастырайық.
Статиканың 1 және 2 аксиомаларының салдарына сүйеніп барлық күштерді олардың әсер ету сызықтарының бойымен О нүктесіне көшіреміз (1.11 ә) сурет). Статиканың 3 аксиомасына сүйеніп және күштерін олардың тең әсерлі күшімен алмастырамыз: .
Алынған күші мен күшін тең әсерлі күшімен алмастырамыз:
.
Осылай барлық күштерді қоссақ, берілген күштер жүйесінің тең әсерлі күші болатын бір күш аламыз (1.11 б) сурет). Бұл күштің векторы былай жазылады:
. (1.2.1)
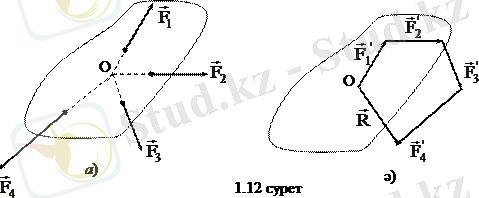
Жинақталатын күштер жүйесінің тең әсерлі күшін күштер көпбұрышын тұрғызу арқылы да анықтауға болады. Түсінікті болу үшін сурет жазықтығында жатқан төрт күш үшін көпбұрыш тұрғызайық (1.12 а) сурет).
күшін масштабпен О нүктесіне күшіне параллель етіп көшіріп, деп белгілейміз. Осы күштің ұшынан күшіне параллель етіп деп белгіленген күшті көшіреміз. Дәл осылай етіп және күштерін көшіреміз.
Жинақталатын күштер жүйесінің тең әсерлісі болатын күші осы күштердің геометриялық қосындысына тең күш ретінде қосылғыш күштердің біріншісінің басын соңғы күштің ұшымен қосатын вектор болады (1.12 ә) сурет).

Жинақталатын күштер жүйесінің тең әсерлі күшін аналитикалық түрде анықтауға болады. Ол үшін геометрияның келесі теоремасына сүйенеміз: күштердің векторлық қосындысының қалаған өске проекциясы қосылғыш күштердің осы өске проекцияларының алгебралық қосындысына тең.
Осыған сәйкес, жинақталатын күштер жүйесін құратын күштердің декарттық координата өстеріне проекцияларын біле отырып тең әсерлі күштің осы өстерге проекцияларын анықтауға болады:
. (1.2.2)
Сонда тең әсерлі күштің модулі мынандай болады:
. (1.2.3)
Оның бағыты бағыттаушы косинустармен анықталады:
. (1.2.4)
Бір жазықтықта орналасқан күштер үшін:
(1.2.5)
(1.2.6)
(1.2.7)
Жинақталатын күштер жүйесінің тепе-теңдік шарттары
Теорема. Қатты денеге түсірілген жинақталатын күштер жүйесі тепе-теңдікте болу үшін оның тең әсерлі күшінің нөлге тең болуы қажет және жеткілікті.
Күштердің тепе-теңдік шарттарын геометриялық немесе аналитикалық түрде келтіруге болады.
1. Тепе-теңдіктің геометриялық шарты. Күштер жүйесінің бас векторы осы күштерден тұрғызылған күштер көпбұрышының тұйықтаушы қабырғасы болғандықтан (1.12 ә) суретті қараңыз), нөлге тең болу үшін көпбұрыштағы соңғы күштің ұшы бірінші күштің басымен дәл келуі керек, яғни көпбұрыш тұйық болу керек.
Демек, жинақталатын күштер жүйесі тепе-теңдікте болу үшін осы күштерден тұрғызылған күштер көпбұрышының тұйық болуы қажет және жеткілікті.
2. Тепе-теңдіктің аналитикалық шарттары. Жүйенің бас векторының аналитикалық модулі (1.2.3) өрнегімен анықталады:
.
нөлге тең болу үшін бір мезгілде болуы керек, яғни осы күштердің координата өстеріне проекцияларының қосындысы нөлге тең. Сондықтан, кеңістіктегі жинақталатын күштер жүйесінің қажет және жеткілікті тепе-теңдік шарттары былай жазылады:
(1.2.8)
(1.2.8) теңдеулері тепе-теңдік шарттарының аналитикалық түрін береді: кеңістіктегі жинақталатын күштер жүйесі тепе-теңдікте болу үшін осы күштердің координата өстерінің үшеуінің әрқайсысына проекцияларының қосындысының нөлге тең болуы қажет және жеткілікті.
Қатты денеге әсер ететін жазықтықтағы жинақталатын күштер жүйесі тепе-теңдікте болу үшін күштердің координата өстерінің екеуіне проекцияларының қосындысының нөлге тең болуы қажет және жеткілікті:
(1.2.9)
Күштің нүктеге (центрге) қатысты моментінің векторы
Күштің әсерінен қатты дене ілгерілемелі немесе айналмалы қозғалыс жасайды. Күштің айналдырушы әсері моментпен сипатталады.
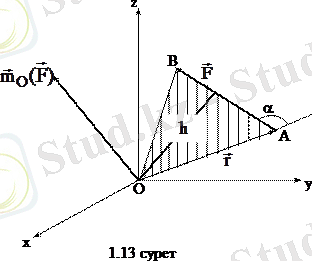
күшінің О нүктесіне (центріне) қатысты моменті деп осы нүктеге түсірілген векторын айтады. Бұл вектордың модулі (шамасы) күш модулі мен күштің нүктеге қатысты иінінің көбейтіндісіне тең, ал бағыты күш пен нүкте арқылы өтетін күш жазықтығына перпендикуляр, оның ұшынан қарағанда күш денені сағат тіліне қарсы бағытта бұратындай болып көрінеді (1.13 сурет).
Күштің О нүктесіне қатысты моментінің шамасы (модулі):
. (1.3.1)
Күштің нүктеге қатысты иіні (h) деп нүктеден күштің әсер ету сызығына дейінгі ең жақын ара қашықтықты (перпендикулярды) айтады.
Күштің О нүктесіне қатысты моментінің векторын күштің түсу нүктесінің радиус-векторы мен күш векторының векторлық көбейтіндісі ретінде жазуға болады:
. (1.3.2)
Екі вектордың векторлық көбейтіндісін анықтауыш түрінде алып, векторының декарттық координата өстеріне проекцияларын анықтаймыз:
.
күшінің О нүктесіне қатысты моменті векторының проекциялары мына түрде жазылады:
(1.3.3)
Халықаралық жүйеде күш моменті ньютон көбейтілген метрмен өлшенеді.

Ос күш және оның моментінің векторы
Қос күш деп модульдері тең, бір біріне қарсы бағытталған екі параллель күштің жүйесін айтады. Қос күштің әсерінен дене айналмалы қозғалыс жасайды, демек, қос күштің моменті болады. Қос күш жатқан жазықтық қос күштің әсер ету жазықтығы деп аталады. Қос күшті құрайтын күштердің әсер ету сызықтарының арасындағы ең жақын ара қашықтық (перпендикуляр) қос күштің иіні (d) деп аталады (1.14 сурет).
Енді жазықтығында жатқан қос күшті қарастырайық. Осы екі күштің кез келген О нүктеге қатысты моменттерінің геометриялық қосындысын алайық:

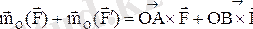
Егер екенін ескерсек мынаны аламыз
.
Алынған өрнек қос күш моментінің векторы деп аталады, ол О нүктесіне тәуелсіз:
. (1.3.4)
Қос күш моментінің модулі оны құрайтын күштердің біреуінің модулі мен қос күш иінінің көбейтіндісіне тең:
.
Қос күш моменті векторының бағытықос күштің әсер ету жазықтығына перпендикуляр, ұшынан қарағанда қос күш денені сағат тіліне қарсы бағытта бұратындай болып көрінеді. Оны кез келген нүктеге түсіруге болады, себебі ол О нүктесіне тәуелсіз, яғни қос күш моментінің векторы - жылжымалы вектор.

Ос күш туралы теоремалар
1-теорема. Бір жазықтықта жатқан екі қос күшті моменті осы қос күштер моменттерінің геометриялық қосындысына тең бір қос күшпен алмастыруға болады (дәлелдеусіз).
Салдар. Бір жазықтықта жатқан кез келген қос күштер жүйесін моменті барлық қос күштер моменттерінің геометриялық қосындысына тең бір қос күшпен алмастыруға болады.
2-теорема. Моменттері тең екі қос күш өзара пара-пар болады (дәлелдеусіз).
1-салдар.Дененің күйін өзгертпейқос күшті параллель жазықтыққа көшіруге болады.
2-салдар.Қос күштің моменті мен айналу бағытын сақтай отырып, оның шамасы мен иінін өзгертуге болады. Одан дененің күйі өзгермейді.
3-теорема.Қиылысатын жазықтықтарда жатқанекі қос күшті осы қос күштер моменттерінің геометриялық қосындысына тең бір қос күшпен алмастыруға болады (дәлелдеусіз)
1, 2, 3 теоремалардың салдары. Түрлі жазықтықтарда жатқан қос күштердің кез келген санын моменті барлық қос күштер моменттерінің геометриялық қосындысына тең бір қос күшпен алмастыруға болады. Сонымен, денеге әсер ететін қос күштер жүйесі бір қос күшке пара-пар екен. Тең әсерлі қос күштің моменті құраушы қос күштердің моменттерінің геометриялық қосындысына тең:
.
Қос күштер жүйесінің тепе-теңдік шарты. Моменттері қос күштердің әсеріндегі дене тепе-теңдікте болу үшін барлық қос күштердің моменттерінің геометриялық қосындысының нөлге тең болуы қажет және жеткілікті:

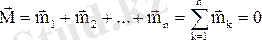
Өзіндік бақылау сұрақтары:
1. Нүктеге (центрге) қатысты күш моментінің векторы.
2. Нүктеге қатысты күш иінінің анықтамасы.
3. Қос күштің, оның иіні мен әсер ету жазықтығының анықтамалары.
4. Қос күш моментінің векторы.
5. Қос күш туралы теоремалар.
6. Қос күштер жүйесінің тепе-теңдік шарты.
Күшті параллель көшіру туралы теорема

Теорема. Дененің бірнүктесіне түскен күшті өзіне параллель етіп басқа нүктеге көшіруге болады. Күштің денеге әсері өзгермеу үшін көшірілген күшке моменті берілген күштің жаңа нүктеге қатысты моментіне тең қос күш қосу керек.
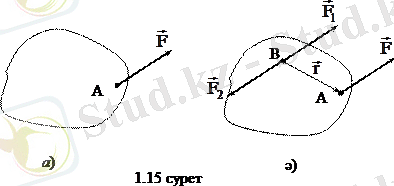
Дәлелдеу. Қатты денеге оныңА нүктесіне түскен күші әсер етсін (1.15 а) сурет). Дененің кез келген В нүктесіне ал болатын және екі теңестірілген күшті түсірейік. Осылайша алынған үш күштің жүйесі В нүктесіне түскен күшіне тең күші мен моменті болатын қос күшті береді (1.15 ә) сурет). Сонымен, теореманың бірінші бөлігі дәлелденді. күшінің В нүктесіне қатысты моментінің векторы былай анықталады:

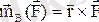
Анықтама бойынша қос күш моментінің векторын былай жазуға болады:

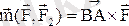
екенін ескерсек, теореманың екінші бөлігі дәлелденеді, яғни

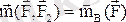
Статиканың негізгі теоремасы
Денеге күштер жүйесі әсер етсін. Осы күштердің геометриялық қосындысы күштер жүйесінің бас векторы деп аталады:
(1.4.1)
Барлық күштердің О нүктесіне қатысты моменттерінің геометриялық қосындысы күштер жүйесінің бас моменті деп аталады:
. (1.4.2)
Теорема. Абсолют қатты денеге әсер ететін кез келген күштер жүйесін берілген О центрге келтіргенде жүйенің бас векторына тең және келтіру центріне түскен бір күшпен және моменті бас моментке тең бір қос күшпен алмастыруға болады.
Дәлелдеу. Қатты дененің нүктелеріне түскен кез келген күштер жүйесін қарастырайық (1.16 а сурет). Күштердің бәрін өзіне өзін параллель етіп бір О нүктесіне көшірейік. Сонда күшті параллель көшіру туралы теоремаға сәйкес әрбір көшірілген күшке бір қос күштен қосу керек (1.16 ә) сурет). Олардың моменттері берілген күштердің О нүктесіне қатысты моменттеріне тең болады, яғни

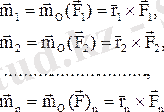
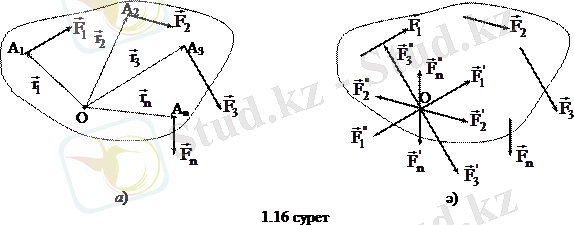
Алынған жинақталатын күштер жүйесін олардың геометриялық қосындысына тең бір күшпен алмастырамыз:

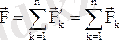
қос күштер жүйесін олардың геометриялық қосындысына тең бір қос күшпен алмастыруға болады:
.
Сонымен, нәтижесінде бір күш пен моменті бір қос күш алдық.

тепе-теңдік шарттары. Вариньон теоремасы
Теорема. Кез келген күштер жүйесі тепе-теңдікте болу үшін оның бас векторының және кез келген центрге қатысты бас моментінің нөлге тең болуы қажет және жеткілікті (дәлелдеусіз):
, . (1.4.3)
Вариньон теоремасы. Егер берілген күштер жүйесінің тең әсерлі күші бар болса, онда тең әсерлі күштің кез келген О центріне қатысты моменті жүйедегі күштердің сол центрге қатысты моменттерінің қосындысына тең.
Өзіндік бақылау сұрақтары:
1. Күшті параллель көшіру туралы теорема.
2. Кез келген күштер жүйесін қандай түрге келтіруге болады?
3. Күштер жүйесінің тепе-теңдік шарттары.
4. Күштер жүйесінің тең әсерлі күшінің моменті неге тең?

ЖАЗЫҚТЫҚТАҒЫ КЕЗ КЕЛГЕН КҮШТЕР ЖҮЙЕСІ
Әсер ету сызықтары бір жазықтықта жатып, кез келген тәртіппен бағытталған күштер жүйесі жазықтықтағы кез келген күштер жүйесідеп аталады. Осындай бір жазықтықта жатқан күштердің жазықтықтың кез келген Онүктесіне қатысты моменттерінің векторлары осы жазықтыққа перпендикуляр болып, бір түзудің бойымен бағытталады. Сонда бұл моменттердің бағыттарын бір бірінен таңбасы бойынша айырып, күшінің О центріне қатысты моментін алгебралық шама ретінде қарастыруға болады. Бұл шаманы деп белгілейміз.

Күштің центрге қатысты алгебралық моменті
күшінің О центріне қатысты алгебралық моменті плюс немесе минус таңбасымен алынған күш модулі мен күштің нүктеге қатысты иінінің көбейтіндісіне тең:
(1.5.1)
Механикада қабылданған оң координата- лар жүйесінде күш денені Оцентріне қатыстысағат тіліне қарсы бағытта бұруға тырысса күш моментінің таңбасы оң, сағат тілімен бағыттас бұруға тырысса - теріс болады. Егер күштің әсер ету сызығы центрден өтсе оның моменті нөлге тең болады (1.17 сурет).
Осы суретте бейнеленген күштер үшін:
, ,

Ос күштің алгебралық моменті

Қос күштің моменті оны құрайтын күштердің біреуінен екіншісінің түсу нүктесіне қатысты алынған моментке тең болғандықтан, бір жазықтықта жатқан қос күштер үшін қос күш моментін де алгебралық шама ретінде қарастыруға болады. Бұл шаманы немесе деп белгілейміз.
Қос күштің алгебралық моменті плюс немесе минус таңбасымен алынған оны құрайтын күштердің біреуінің модулі мен қос күш иінінің көбейтіндісіне тең:
. (1.5.2)
Егер қос күш денені сағат тіліне қарсы бағытта бұруға тырысса қос күш моментінің таңбасы оң, ал сағат тілімен бағыттас бұруға тырысса - теріс болады (1.18 сурет).
1.18 суретте бейнеленген ( ) және ( ) қос күштер үшін:
,

Қос күштің моменті оның денеге әсерін толық сипаттайды. Сондықтан, кейде қос күшті оның моментінің айналдыратын бағытын көрсететін доғалық тіл ретінде бейнелейді (1.19 сурет) ( ).
1.5.3 Жазықтықтағы кез келген күштер жүйесінің
Бас векторы мен бас моменті
Жазықтықтағы кез келген күштер жүйесі үшін де бас вектор барлық күштердің геометриялық қосындысы болады және декарттық координаталар жүйесінің екі өсіне проекцияланады:
. (1.5.3)
Бас вектордың сан шамасы (модулі) мына өрнекпен анықталады:
, (1.5.4)
ал бағыты бағыттаушы косинустардың көмегімен анықталады:
(1.5.5)
Бұл жағдайда да О нүктесіне қатысты бас момент барлық күштердің О нүктесіне қатысты моменттерінің алгебралық қосындысы болады:
. (1.5.6)
Егер денеге күштермен қатар қос күштер әсер етсе, олардың моменттері жүйенің бас моментіне қосылады.
Жазықтықтағы кез келген күштер жүйесінің тепе-теңдік шарттары
Күштер жүйесінің жалпы тепе-теңдік шарттарынан жазықтықтағы кез келген күштер жүйесінің векторлық тепе-теңдік шарттары алынады:
.
Бұл шарттарды аналитикалық түрде жазуға болады.
1. Жазықтықтағы кез келген күштер жүйесі тепе-теңдік шарттарының бірінші түрі: жазықтықтағы кез келген күштер жүйесі тепе-теңдікте болу үшін барлық күштердің күштер жазықтығында алынған екі өске (х пен у) проекцияларының қосындысы мен барлық күштердің кез келген О центріне қатысты моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті:
. (1.5.7)
2. Жазықтықтағы кез келген күштер жүйесі тепе-теңдік шарттарының екінші түрі: жазықтықтағы кез келген күштер жүйесі тепе-теңдікте болу үшін барлық күштердің күштер жазықтығындағы өске (х) проекцияларының қосындысы мен барлық күштердің осы өске перпендикуляр түзуде жатпайтын екі нүктеге (А және В) қатысты алынған моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті:
. (1.5.8)
3. Жазықтықтағы кез келген күштер жүйесі тепе-теңдік шарттарының үшінші түрі: жазықтықтағы кез келген күштер жүйесі тепе-теңдікте болу үшін барлық күштердің бір түзудің бойында жатпайтын үш нүктеге (А, В және С) қатысты алынған моменттерінің алгебралық қосындысы нөлге тең болуы қажет және жеткілікті:
. (1.5.9)
Егер күштің нүктеге қатысты иінін анықтау қиын болса, онда күшті құраушыларға жіктеп, Вариньон теоремасын қолданған абзал.
Таралған күштер. Қатаң бекітпе. Денелер жүйесінің тепе-теңдігі
Дененің бір нүктесіне түскен күш қадалған күш деп аталады. Бұдан басқа түзу бойына, жазықтық бетіне немесе көлемге түскен күштер де бар. Мұндай күштер таралған күштер немесе жүктемелер деп аталады.
Инженерлік есептеулерде әртүрлі заңдылықпен таралған жүктемелерді жиі кездестіруге болады. Енді бір жазықтықта жатқан таралған күштердің кейбір қарапайым түрлерін қарастырайық.
Жазықтықтағы біркелкі таралған күштер жүйесі жүктелген кесіндінің ұзындық бірлігіне келетін күш шамасымен, яғни таралу қарқындылығымен сипатталады. Қарқындылық ньютон бөлінген метрмен (Нм) өлшенеді.
1) Түзу сызық бойымен біркелкі таралған күштер (1.20 сурет).

Біркелкі таралған күш (жүктеме) депәсері түзу сызық бойымен біркелкі таралған күшті айтады (1.20 сурет). Мұндай күштер үшін қарқындылықтың мәні тұрақты болады. Статикалық есептеулерде бұл күштер жүйесін тең әсерлі күшпен алмастырады. Оның түсу нүктесі жүктелген кесіндінің ортасы болады, ал модулі:
. (1.5.10)
2) Түзу бойымен сызықтық заңымен ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.