Экономикада матрицалық алгебра: ресурстарды бөлу және шикізат шығындарын есептеу

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 3 бет
Таңдаулыға:

Уразбекова Меруерт

Финансы

19651

Бұл мақалада біз матрицаларды экономикада пайдалануды қарастырамыз. Бұл үшін бізге экономикалық міндеттердің шешімін талдап, белгілі бір қорытынды жасау қажет.

Матрица-қиылысында оның элементтері бар жолдар мен бағандардың жиынтығын білдіретін сақина немесе өріс элементтерінің тікбұрышты кестесі түрінде жазылатын математикалық объект. Матрицалар жолдар мен бағандар саны матрицаның өлшемін анықтайды.

Матрицалар математикада сызықты алгебралық немесе дифференциалдық теңдеулер жүйесін жинақы жазу үшін кеңінен қолданылады. Бұл жағдайда матрица жолдарының саны теңдеулердің санына, ал бағандар саны белгісіз сандар санына сәйкес келеді. Нәтижесінде, сызықтық теңдеулер жүйесін шешу матрицалар операцияларына түседі.

Матрица ұғымы және оған негізделген математика бөлімі - матрицалық алгебра - экономистер үшін өте маңызды. Бұл экономикалық объектілер мен процестердің математикалық үлгілерінің едәуір бөлігі қарапайым, ал ең бастысы - ықшам матрицалық формада жазылатындығымен түсіндіріледі.

Матрицалардың көмегімен кейбір экономикалық тәуелділіктерді жазу ыңғайлы. Мысалы, экономиканың жекелеген салалары бойынша ресурстарды бөлу кестесі (шарт. бірл. ) :

Электроэнергия

5, 3

4, 1

Электроэнергия: Еңбек ресурсы

5, 3: 2, 8

4, 1: 2, 1

Электроэнергия: Су ресурсы

5, 3: 4, 8

4, 1: 5, 1

Ресурстар

Экономика салалары

Өнеркәсіп

Ауыл шаруашылығы

Электр энергиясы

5, 3

4, 1

Еңбек ресурстары

2, 8

2, 1

Су ресурстары

4, 8

5, 1

Салалар бойынша ресурстарды бөлу матрицасы түрінде ықшам нысанда жазылуы мүмкін:

А=

5, 3

4, 1

5, 3: 2, 8

4, 1: 2, 1

5, 3: 4, 8

4, 1: 5, 1

Бұл жазбада, мысалы, А11 = 5, 3 матрицалық элемент өнеркәсіп қанша электр энергиясын пайдаланатынын көрсетеді, ал а22 = 2, 1 элемент - ауыл шаруашылығы қанша еңбек ресурстарын тұтынатынын көрсетеді.

Келесі тапсырманы қарастырайық: кәсіпорын өнімді үш түрді шығарсын: P1, P2, P3 және шикізатты екі түрді қолдансын: S1 және S2. Шикізат шығынының нормалары матрицамен сипатталады:

мұнда аіј (i = 1, 2, 3; j = 1, 2) әрбір элементі j-типті шикізат бірлігінің i-түрдегі өнім бірлігін өндіруге қанша жұмсалатынын көрсетеді. Өнімді шығару жоспары матрицамен-с = (100 80 130) жолымен берілген, Шикізаттың әр түрінің бірлігінің құны (ден. бірлік) - матрица бағанасы:

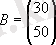Есепті қарап, алды: 1-ші шикізат шығындары S1 құрайды = 2·100 + 5·80 + 1·130 = 730 бірлік және 2 - ші-S2 = 3·100 + 2·80 + 4·130 = 980 бірл., сондықтан матрица-шикізат s жолы жұмыс ретінде жазылуы мүмкін:

Сонда шикізаттың жалпы құны Q = 730·30 + 980·50 = 70900 den. бірл. матрицалық түрде жазылуы мүмкін: Q = S·B = (CA) B = (70900) .

Шикізаттың жалпы құнын басқа тәртіппен де есептеуге болады: алдымен өнімнің бірлігіне шикізат шығындары құнының матрицасын, яғни матрицаны есептейміз. :

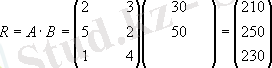
содан кейін шикізаттың жалпы құны:

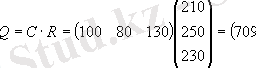
Бұл мысалда біз матрицалардың туындыларын ассоциативті заңның орындалуына көз жеткіздік: (СА) В = С(АВ) .

Матрицалардың экономикада қолданылуына талдау жасай отырып, біз матрицалардың артықшылықтары стратегиялық маңызы бар айнымалылардың кең жиынтығын пайдаланатыны; ресурстар қозғалысының бағытын көрсетеді деген қорытындыға келдік. Бұл құралдың кемшіліктері арасында: арнайы стратегияларды әзірлеу бойынша нақты ұсынымдарды қамтамасыз етпейді; ол бойынша жеңімпаз болуға дайын бизнес саласын анықтау мүмкін емес. Сонымен қатар матрицалар еңбек пен уақыттың аз шығындарымен үлкен және әртүрлі статистикалық материалды, әлеуметтік-экономикалық кешеннің деңгейін, құрылымын, ерекшеліктерін сипаттайтын әртүрлі бастапқы деректерді өңдеуге мүмкіндік береді.

Сонда шикізаттың жалпы құны Q = 730·30 + 980·50 = 70900 den. бірл. матрицалық түрде жазылуы мүмкін: Q = S·B = (CA) B = (70900) .

содан кейін шикізаттың жалпы құны:

Бұл мысалда біз матрицалардың туындыларын ассоциативті заңның орындалуына көз жеткіздік: (СА) В = С(АВ) .

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.