Орта мектеп геометрия курсында жазықтықтағы геометриялық түрлендірулерді оқытудың әдістемелік ерекшеліктері


Н. С. Серіков
Абай атындағы Қазақ ұлттық педагогикалық университеті, Алматы қ, Қазақстан
НЕГІЗГІ МЕКТЕП ГЕОМЕТРИЯ КУРСЫНДА ЖАЗЫҚТЫҚТАҒЫ ТҮРЛЕНДІРУЛЕРДІ ОҚЫТУДЫҢ ӘДІСТЕМЕЛІК ЕРЕКШЕЛІКТЕРІ
Аңдатпа
Дәстүрлі оқытуда аналитикалық әдістердің басым болуы, оқушыларға айқын болып көрінетін нақты нәрселердің күрделеніп дәлелденуі - білім алушылардың геометрияны түсінуін қиындатады.
Геометриялық түрлендірулердің орта мектепте оқытудағы ұтымды тұстары: айналамыздағы өмірден алынады және табиғи құбылыстардың өзара байланыстарының жалпы заңдылықтарының көрінісі. Сондықтан мектеп курсында геометриялық түрлендірулер дәйекті қолдану геометрияның пәндік-логикалық материалының нақты мазмұнын түсінуге көмектеседі.
Түйін сөздер: геометриялық түрлендірулер, геометриялық түрлендіруге есептерді шешу әдістері, жазықтықтағы геометриялық түрлендірулер түрлері.
Аннотация
С. Н. Сериков
Казахский национальный педагогический университет имена Абая, г. Алматы, Казахстан
МЕТОДОЛОГИЧЕСКИЕ ОСОБЕННОСТИ ОБУЧЕНИЯ ПРЕОБРАЗОВАНИЯМ НА ПЛОСКОСТИ В ОСНОВНОЙ ШКОЛЕ КУРСА ГЕОМЕТРИИ
Преобладание аналитических методов решения задач, усложненное доказательство очевидного в традиционном обучении - затрудняет изучение геометрии у обучающися.
Преимущества геометрических преобразований в школьном курсе геометрии: они часто встречаются в окружающей нас жизни и являются отражением законов взаимодействия природных явлений. Поэтому последовательное применение геометрических преобразований в школьной программе помогает понять содержание предмето-логического материала геометрии.
Ключевые слова: геометрические преобразования, методика решения задач на геометрические преобразования, виды геометрических преобразований на плоскости.
Ғылыми-әдістемелік әдебиеттерді, мұғалімдердің пікірлерін және жеке зерттеу тәжірибесін талдау орта мектептегі геометрия көптеген оқушылар үшін шешілмейтін тосқауылға айналып келе жатқандығын көрсетеді.
Бұл жағдайдың болу себебі: дәстүрлі оқытуда аналитикалық әдістердің басым болуы, оқушыларға айқын болып көрінетін нақты нәрселердің күрделеніп дәлелденуі - білім алушылардың геометрияны түсінуін қиындатады.
Геометриялық есептерді шешу әдістері:
- Геометриялық
- Алгебралық
- Комбинациялық
Геометриялық әдісті қолданғанда логикалық ойлаудың көмегімен қажетті теоремалар арқылы тұжырымдарды дәлелдейміз. Есептерді алгебралық әдіспен шешкенде ізделген шаманы табу тікелей есептеу жолымен, сонымен қатар, теңдеу немесе олардың жүйесін құрып шешу арқылы жүзеге асырылады.
Жазықтықтағы фигуралардың өлшемдерін анықтап және қасиеттерін оқып-үйренумен қатар, олардың түрлендіруін де қарастыру қажет.
Мектеп курсында қарастырылатын геометриялық түрлендірулер - осьтік, орталық симметрия, параллель көшіру, бұру, ұқсастық, гомотетия болып табылады.
Геометриялық түрлендірулердің орта мектепте оқытудағы ұтымды тұстары: айналамыздағы өмірден алынады және табиғи құбылыстардың өзара байланыстарының жалпы заңдылықтарының көрінісі. Сондықтан мектеп курсында геометриялық түрлендірулер дәйекті қолдану геометрияның пәндік-логикалық материалының нақты мазмұнын түсінуге көмектеседі.
«Геометриялық түрлендірулердің маңыздылығы:
- практикалық операциялар ойлау қабілетін дамытуда маңызды рөл атқарады;
- геометриялық түрлендірулер - бұл функция ұғымын жалпылау ғана емес, оларды зерттеу, геометрияның жеке бөліктерін де, олардың өзара байланыстарын да бір көзқараспен қарау мүмкіндігін ашады;
- геометриялық түрлендірулердің жалпылығы көптеген теремалардың дәлелін айтарлықтай жеңілдетеді;
- геометриялық түрлендірулер тек геометрия курсында ғана емес, алгебра (сызбалық функциялар), физика (механика, оптика), химия (кристалдық денелер), сурет салу (түрлі проекцияларда кескін құру) және т. б. мектеп курсында қолданылады, яғни геометрияның басқа пәндермен пәнаралық байланысын көрсетеді». [5, с. 2-4]
Осының бәрі көрнекілікті, тәжірибелік конструктивті әрекетті және логикалық талдауды үйлестіре отырып, геометрияны оқыту әдістемесін жасау қажеттілігін туындатады.
Осылайша, геометриялық түрлендіру әдісі жүйелі курсты оқытуда сындарлы тәсілді жүзеге асыру ретінде кеңістік ойлауың дамауына ықпал етеді.
«А. Н. Колмагоров былай деп жазды: « . . . функция ұғымы - қазіргі математикада жиі қолданатылатын ұғымдардың бірі. Геометриялық түрлендірулер де - функция болып табылады. Сондықтан мектеп геометриясында түрлендірулері қолдануды елемеу дұрыс болмас». [3, 21 б. ]
Мектептегі тәжірибеде екі нүктенің арасындағы қашықтықтың теңдігін сақтайтын түрлендірулерге көп көңіл бөлінеді, тиісті терминдерге назар аударылады.
Ең бастысы бұл материалды геометрия курсында басқа тақырыптарды өткенде пайдалану, бұл үшін түрлендірулердің өзара байланысуын зерттеуге назар аудару қажет.
Геометриялық түрлендіруді қолдану арқылы шығарылатын есептердің екі түрлісі болады:
1) геометриялық түрлендірулердің қасиеттерін пайдалануға байланысты есептер;
2) геометриялық түрлендірулер туралы айтылмайтын, бірақ оларды қолдану арқылы шешілетін есептер.
Bilimlаnd порталынан, мысалдар: [4]
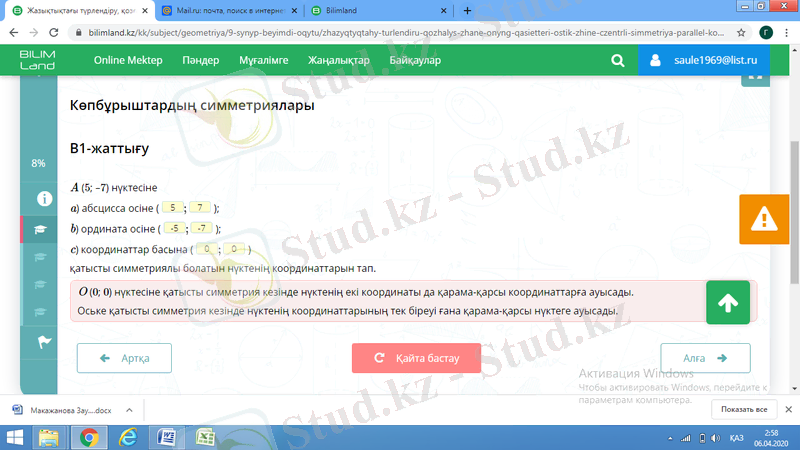
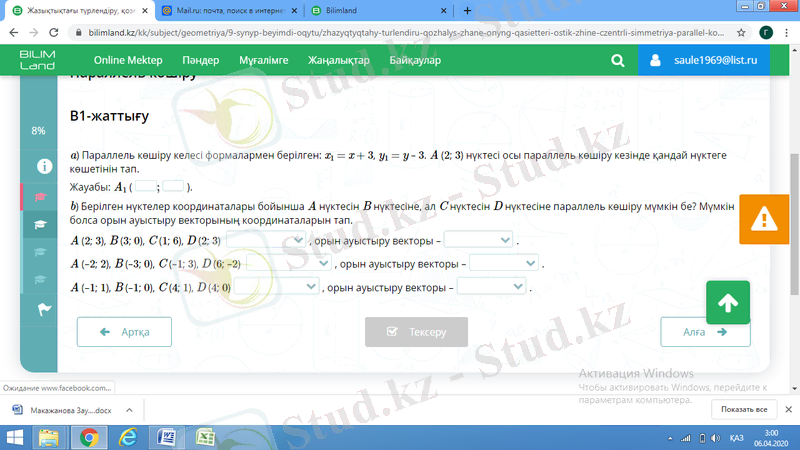
Ұқсастар әдісін қолдану.
Бұл әдісте қосымша сызбалар арқылы пайда болған ұшбұрыштардың ұқсастығы қолданылады.
Есеп: KMN ұшбұрышына ромб кіріктірілген, К бұрышы - ортақ, ромбтың Е төбесі MN қабырғасында орналасқан. Егер KM =m, KN=n болса, ромбтың қабырғасының ұзындығын табыңдар. [1, 480 б. ]
Шешуі:
M
MDE ~ EPN
D E
K
P N
Жауабы:
«Шеңберді мысалға ала отырып бейне және кері бейне ұғымдарын еңгізіп алуға болады.
Анықтама:
Егер жазықтықтың әрбір Х нүктесі қандай да бір заңдылықпен осы жазықтықтық У нүктесіне бейнеленсе, онда жазықтықта геометриялық түрлендіру берілген дейміз. Бұл жағдайда Х және У нүктелері әртүрлі және Х нүктесі У нүктесіне бейнеледі». [6, с. 1]
Білім алушылардың көрнекі сызбалар арқылы эстетикалық талғамын шыңдау, симметрияны түсіне білу, жинақылыққа, ұқыптылыққа тәрбиелеу, ұлттық мәдениетке деген қызығушылығын арттыру мақсатында түрлі дидактикалық құралдарды қолданған дұрыс болады. Мысалы, симметрияға байланысты:
Тапсырма: Табиғаттағы, химиядағы, математикалық, архитектурадағы, қазақ ұлттық ою өрнегіндегі симметрия туралы мәлімет бере отырып, мысалдар келтір.
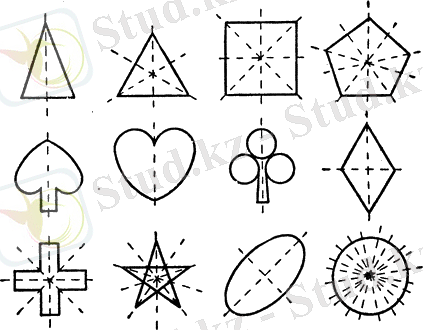
Тапсырма: Суреттегі тең пішіндерді көрсет [7]
Жаңартылған оқу бағдарламасына сәйкес, «Жазықтықтағы түрлендірулер» бөлімі бойынша тоқсандық жиынтық бағалаудан оқу мақсаттары мен тапсырмалардан мысал:
«Оқу мақсаты:
9. 1. 4. 9 Симметрия, параллель көшіру және бұру кезінде фигуралардың бейнелерін салу;
9. 1. 4. 13 Ұқсас фигуралардың анықтамасын және қасиеттерін білу;
9. 1. 4. 15 Тікбұрышты үшбұрыштардың ұқсастығын білу және қолдану;
9. 1. 4. 17 Ұқсас фигуралардың аудандары және ұқсастық коэффициенті арасындағы тәуелділік формуласын білу;
Бағалау критерийі:
Білім алушы
- Есеп шығаруда тік бұрышты үшбұрыштардың ұқсастығын қолданады;
- Ұқсас фигуралардың аудандары және ұқсастық коэффициенті арасындағы тәуелділік формуласын қолданады;
- Берілген фигураны түрлендіреді;
- Есеп шығаруда ұқсас фигуралардың қасиеттерін қолданады;
Тапсырма
- АВСжәнеСЕDүшбұрыштары берілген. АВ= 6 см, ВС= 2 см жәнеСD= 2, 5 см болса, ЕDтабыңыз.
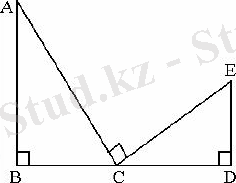
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz