Кешенді сандар теориясының туындау және қалыптасу тарихының элементтері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

1. 1 Кешенді сандар теориясының туындау және қалыптасу тарихының элементтері

Адамзат әрқашан қандай да бір тапсырмалардың орындалмау мәселесімен кездесіп отырған және оларды орындау жолдарын іздегенімен, бірде тауып, бірде таппаған. Мысалы, математикада кез келген 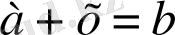теңдеуінің түбірі болуы үшін оң сандар жеткіліксіз болып шықты, сондықтан да біздің дәуірімізге дейінгі екінші ғасырда Қытай математиктері теріс сандарды енгізген. Теріс сандар шамалардың өзгерісін бір жолмен сипаттауға көмектесті.

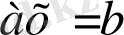тәрізді теңдіктерді шешу үшін бөлшек сандарды енгізу қажет болды. Б. д. д. екі мыңжылдық бұрын Көне Египет пен Көне Вавилонда бөлшектер қолданыла бастағаны белгілі [10] .

Біздің дәуіріміздің VIII ғасырында оң саннан алынатын квадраттық түбірдің екі мәні болуы мүмкін екендігі анықталды, яғни олар оң және теріс мәндер, оның үстіне теріс сандардан квадраттық түбірді шығару мүмкін емес: мысалы, 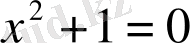теңдігі орындалуы үшін 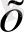саны болмайды. XVI ғасырда кубтық теңдеулерді зерттеу кезінде теріс сандардан квадраттық түбір шығару қажет екендігі анықталды. 1545 жылы итальяндық математик Д. Кардано (1501-1576) жаңа түрлі сандарды енгізуді ұсынды. Ол нақты сандар жиынтығында шешімі жоқ 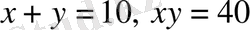теңдеулер жүйесінің болған кезде әрқашан шешімі бар екендігін көрсетті, тек мұндай мәндермен қарапайым алгебра ережелері бойынша операциялар жасап, 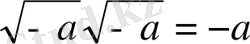деп есептеу қажет [28] . Кардано ондай шамаларды «таза теріс» және тіпті «сопылық теріс» деп те атаған және оларды түкке қажет емес деп есептеген, оларды қолдануға тырыспаған да, себебі ондай сандар арқылы қандай да бір шаманың өзгеріс нәтижесін, немесе сол шаманың өзгерісінің өзін белгілеуге болмайды. Алайда 1572 жылдың өзінде итальяндық алгебраист Р. Бомбелли (1526-1572) кітабы шыққан, онда осындай сандармен жасалатын арифметикалық операцияларының алғашқы ережелері белгіленген, тіпті олардан кубтық түбірді шығару ережелері де жазылған. Ары қарай кешенді сандар алгебраның әр түрлі сұрақтарында қолданылған, алайда тәжірибеде әлі пайдаланылмаған. «Жорамал сандар» атауын 1637 жылы француз математигі және философ Рене Декарт енгізген [35] .

Жалпы XVI ғасыр мен келесі ұрпақ математиктері ХІХ ғасырдың басына дейін кешенді сандарға күмәнмен қараған. Олар ол сандарды «жорамал» (Рене Декарт), «өмірде жоқ», «ойлап шығарылған», «тым көп данагөйліктен пайда болған» (Д. Кардано) деп есептеген [10] . Г. Лейбниц ол сандарды «құдай рухының көркем әрі керемет баспанасы» деп атаған, ал о дүние белгісі деп есептеген (тіпті ол белгіні өзінің моласына сызсын деп айтып кеткен) .

Аталған кезеңдегі көптеген ғалымдар кешенді сандарды түзу сызықта пайдаланып, оны жазықтықтық бейнелеуді талап етпейтін температура, уақыт және т. б. тәрізді түсініктерге қатысты қолдануға тырысқан [28] .

Кейінірек Л. Эйлер (1707-1783) математикаға 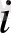белгісін енгізген, ондағы 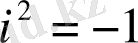( 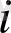- латынның imaginarius сөзінің бірінші әріпі және ол «жорамал», «ойлап табылған» дегенді білдіреді) [10] .

Сондай-ақ Л. Эйлер 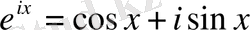формуласын енгізіп, кейін ол оның атымен аталған, алайда ол формулаға Эйлерге дейін ағылшын математигі Р. Котес (1682-1716) иелік еткен [35] . Ол формула:

- экспоненциалды функцияның периодтығын дәлелдеуге;

- кешенді сандардың логарифмдерін шығаруға көмектескен.

Кешенді деп аталған жаңа сандар жиынтығының қаталдау теориясын неміс ғалымы Карл Гаусс (1777-1855) одан әрі дамытып, оларға түсінуге көп көмектесетіндей геометриялық түсініктеме беріп кеткен. Алайда Гауссқа дейін геометриялық түсінікті даттық жер өлшеуші К. Весельде (1745-1818) және француз математигі Арганда (1768-1822) да кездескен. К. Гаусс 1831 жылы кешенді сандарға толықтай негіздеме беріп, олардың математикадағы қосымшаларын ұсынған. Кешенді сандардың жазықтықтағы жазықтық нүктелері мен векторлары көмегімен көрнекі геометриялық бейнесі пайда болғаннан кейін (Гаусс 1831 ж., Вессель 1799 ж., Арган 1806 ж. ) жаратылыстанудың көптеген тапсырмаларын, әсіресе гидро- және аэродинамика, электромеханика, серіппелік және беріктік теориялары, сондай-ақ геодезия мен картография тапсырмаларын осы кешенді сандар мен олар бар теңдіктермен белгілеу мүмкін бола бастады. Дәл осы уақыттан бастап «жорамал» немесе кешенді сандардың бар екендігі жалпымен қабылданған фактіге айналып, нақты сандар тәрізді шынайы мазмұнға ие бола бастады.

ХІХ ғасырда О. Коши (1789-1857), Г. Риман (1826-1866) және К. Вейерштрасс (1815-1897) кешенді сандар негізінде жаңа математикалық пәнді жасап шығарды, ол кешенді айнымалының функциялары теориясы деп аталады және қазіргі заманғы математикада үлкен рөл атқарады [28] .

Ғылым мен техниканың дамуы барысында кешенді сандарсыз көптеген тәжірибелік істерді атқару мүмкін емес екендігі айқын бола бастады. Кешенді сандар электротехника, гидродинамика, картография, ұшақ теориясы мен басқа да салаларда кеңінен қолданысын тапты. Кешенді айнымалының функциясы теориясына ресейлік және кеңестік ғалымдар да үлкен үлес қосты: Р. И. Мусхелишвили оның серіппелік теорияға қосымшалығымен айналысты, М. В. Келдыш и М. А. Лаврентьев - оның аэродинамика мен гидродинамикаға, Н. Н. Боголюбов и В. С. Владимиров - өрістік кванттық теориясы мәселелеріне қосымшалығын зерттеген. Қазір кешенді сандар қолданылмайтын физика, механика салаларын немесе техникалық пәндерді атау өте қиын десе де болады [35] .

Айта кететін жайт, кешенді сандардың танымдық және тәжірибелік мәні зор. Оларды орта жалпы білім беретін мектептің математика курсында зерттеу өте өзекті болып табылады [10] .

1. 2 Кешенді сан ұғымы мен оларға қолданылатын амалдар

Кешенді сандардың математикада атқаратын рөлі зор. Кешенді сандар ұғымы квадрат теңдеудің дискриминанты нольден кіші болған жағдайда оның нақты сандар R жиынында түбірі болмайтынына байланысты пайда болған. Кешенді сандардың негізін құрайтын қазіргі математикада $i$ деп белгіленетін сан $x^{2} + 1 = 0$ теңдеуін қанағаттандырады. Сонымен $i$ деп белгілегеніміз, $i^{2} = - 1$ болатын, бұрын кездеспеген жаңа сан. Кешенді сандар алгебралық теңдеулерді шешу негізінде пайда болады. Сондықтан кешенді санның алгебралық түрін қарастыра кетсек.

Элементтері нақты сандардың реттелген қостары болатын жиынды қарастырамыз. Осы жиында екі қостың көбейтіндісі деген екі амалды енгіземіз.
$< a, b > + < c, d \geq < a + c, b + d >$ (1)

$< a, b > \bullet < c, d > = < ac \bullet bd, ad \bullet bc >$ (2)

Анықтама: Кешенді сандар деп (1) және (2) формулалары арқылы қосу және көбейту амалдары анықталған нақты сандардың реттелген қостары деп атайды.

$Z = < a, b >$

Кешенді сандар жиыны С деп белгіленеді.

$N \subset Z \subset Q \subset R \subset C$

Кешенді сандар алгебралық теңдеулерді шешу негізінде пайда болады.

$Z = < a, b > = < a, 0 > + < 0, b > = < a, 0 > + < b, 0 > \cdot < 0, 1 >$

$< a, 0 > = a, \ \ \ \ \ < b, 0 > = b, \ \ \ \ \ \ < 0, 1 > = i$

$Z = < a, b > = a + bi$

$Z = a + bi$ кешенді санның алгебралық түрі болып табылады. Мұндағы $a -$ кешенді санының нақты бөлігі, $b -$ кешенді санының жорамал бөлігі.

Анықтама. $Z_{1} = a + bi$ және $Z_{2} = c + di$ кешенді сандарының нақты бөлігі нақты бөлігіне, жорамал бөлігі жорамал бөлігіне тең болса, онда олар өзара тең деп аталады.

Анықтама. Жорамал бөлігінің таңбасы арқылы ажыратылатын екі кешенді сан өзара түйіндес сандар деп аталады.

Кешенді сандарға амалдар қолдану.

1. Қосу (азайту) амалы: $Z_{1} = a + bi$ , $Z_{2} = c + di$ .

Екі кешенді санды қосу (азайту) үшін олардың нақты бөліктерін өзара, жорамал бөліктерін өзара қосу (азайту) керек. Кешенді санның қосындысы немесе айырмасы кешенді сан болады:

$Z_{1} \pm Z_{2} = (a + c) \pm (bi + di) = (a + c) \pm (b + d) i$