ФИБОНАЧЧИ САНДАРЫН ЕСЕП ШЫҒАРУДА ПАЙДАЛАНУ

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

МРНТИ 27.01.45
ФИБОНАЧЧИ САНДАРЫН ЕСЕП ШЫҒАРУДА ПАЙДАЛАНУ

Ильясов И.И , физика-математика ғылымдарының кандидаты, доцент1
Утегенова А.Т ., математика мамандығының магистранты2
М.Өтемісов атындағы Батыс Қазақстан мемлекеттік университеті, Орал қаласы.
The-life-is-perfect@mail.ru

Аннотация. Бұл мақалада Фибоначчи сандарының шығу тарихы және олардың қасиеттері дәлелдемелермен келтірілген. Фибоначчи сандарының қасиеттері мысал ретінде әр түрлі тапсырмаларда қолданылуы қарастырылған.

В данной статье рассматриваются происхождения чисел Фибоначчи и их свойства доказательствами. А также, тесно связанный с этой темой, феномен золотого сечения, в котором большинство ученых видят одно из наиболее ярких, давно уже замеченных человеком проявлений гармонии природы. Приведены решения задач на использование свойств чисел Фибоначчи.

This article discusses the origins of Fibonacci numbers and their properties by proofs. And also, closely related to this topic, the phenomenon of the Golden ratio, in which most scientists see one of the most striking, long-noticed by man manifestations of the harmony of nature. The solutions of problems on the use of properties of Fibonacci numbers are given.

Кілттік сөздер. Фибоначчи сандары, Фибоначчи сандарының қасиеттері, Абак, сандық тізбек, бүтін сандар, рекуренттік тізбек, сиқырлы пропорция, PHI саны.

1202 жылы орта ғасыр дәуірінің ең ірі еуропалық математигі Леонардо Пизанскийдің (Фибоначчи есімді лақап атымен көбірек танымал - Боначчи ұлы) атақты Абақ туралы кітабы жарық көрді (Абақ - есеп тақтасы.). 459 беттен тұратын бұл көлемді еңбек сол кездегі математикалық білімнің нағыз энциклопедиясына айналды және келесі бірнеше жүзжылдықтарда математиканың Батыс Еуропада дамуында үлкен рөл атқарды. "Liber abaci" немесе арифметика бойынша трактат (дәл осылай атауына болады, өйткені Леонардо абаком деп санақ тақтасын емес, арифметиканы түсінді) арифметикалық және алгебралық мәліметтердің толық қамтылу және баяндалу тереңдігімен ерекшеленді. Бұл кітапта сандар мен оларға қолданылатын амалдар туралы ғана емес, сонымен қатар теңдеулерді шешу жөніндегі есептерге байланысты алгебраға да түсінік берілді. 1,388
Автор кітапта символдар мен формулаларды баяндап қана қоймай, есептер мен мысалдарды түсіндірмелерімен немесе пайдалы түсініктемелерімен қоса жазған. Негізінен кітап оқырмандардың кең тобына: көпестерге, есеп жүргізушілерге, сатушыларға, шенеуніктерге және т. б. арналған болуы керек. Алайда, "Liber abaci" деп аталатын туынды көптеген адамдар үшін қиын болды, сондықтан 1228 жылы Леонардо Пизанский кітаптың жетілдірілген басылымын ұсынды. Пизанский ұсынған трактат еуропалық ғалымдардың Үнді және араб математиктерінің алгебра мен сандар теориясын зерттеуінде одан әрі дамуына елеулі әсер етті. Бұл кітапта арифметика және алгебра бойынша негізгі мағлұматтарды қамтиды, яғни кейіннен Фибоначчи сандары аталып кеткен сандық тізбектердің қасиеттері қамтылған.
Фибоначчи сандарының шығу тарихы бір жылда бір жұптан қанша жұп үй қояны туады есебімен байланысты. Өзінің Абақ туралы кітабында мынадай есепті қарастырды (үй қояндарының көбеюі туралы.):
Егер әрбір жұп қоян ай сайын бір жұп көжектен туатын болса және кейінгі жұп бір ай өткен соң өзі де осылай өсіп өнсе, оның үстіне бірде - бір көжек шығынсыз болса, онда бір жылда бастапқы бір жұп қояннан қанша қоян өсіп өнетінін табу керектігі талап етіледі. 2,136
Осы есепті шығарылу барысында Фибоначчи сандарының тізбегін аламыз.
u1,u2,u3,...,un1
(1) түріндегі тізбек Фибоначчи қатары деп аталады. Бұл қатарға
u1=1, u2=1 2
шарт қойылады да,
un+2=un+1+un (3)
Фибоначчи сандарының n - ші мүшесін табудың рекурентті формуласы ұсынылады.
Фибоначчи қатары деп бірінші және екінші мүшелерінің әрқайсысы 1-ге тең, ал 3- інші мүшесінен бастап әрбір мүшесі алдынғы екі мүшесінің қосындысына тең болатын сандарды айтамыз.
1,1,2,3,5,8,13,21,34,55,89,144,233, 377,610,987,1597,...,
Фибоначчидің ғылым тарихында із қалдыруға осы есептің өзі жеткілікті болар еді. Ғалымның есімі осы есепке байланысты бүгінде көп айтылады.
Математиктер үшін бұл ең алдымен рекурренттік тізбектің классикалық мысалы болып табылады. Нәтижесінде осы реттілік тіршілікте жиі кездесіп, қызықты қасиеттерін көрсетеді. Қояндар мұның тек бір мысалы.
Фибоначчидің бұл тапсырмасы ересек қоян жұбына арнап қарастырғанын ескеру керек, себебі есептің шарты бойынша қояндар екінші айдан бастап туады. Осы мәселеге ұқсас есепті бір ғасыр жарымнан кейін үнді математигі Нарайана қарастырды: егер әр жылдың басында сиыр бұзау әкелсе, ал бұзау үш жасқа толғаннан кейін өзі де осылай өсіп өнсе, бір сиырдан 20 жыл ішінде келетін сиыр мен бұзаудың санын табу керек. Егер мәселе есепті рекуренттік қатынас құру арқылы шешсек, онда 1, 1, 1, 2, 3, 4, 6, 9, 13, ... тізбегіне келеміз. 3
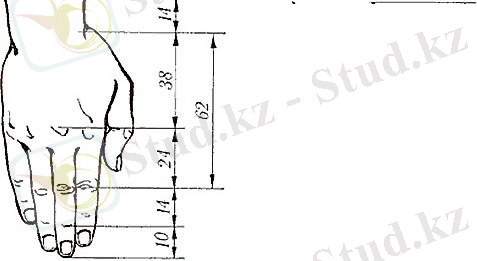
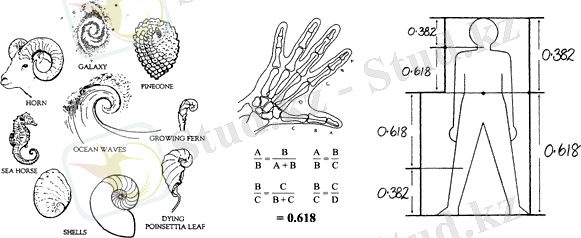
Осы Фибоначчи қатарының ерекшелігі оның кез-келген қатар тұрған екі мүшесінің қатынасы шамамен 1,6-ға тең, бұны басқаша PHI саны деп атайды. Бұны Сиқырлы пропорция дейді. Сиқырлы пропорция өте ерте кезден белгілі болған. Ертедегі PHI санын ашқан адамдар жаратушыны дүниені жарату үшін пайдаланған құрлыс тасын таптық деп сеніп, табиғатқа сене бастаған. Себебі, біз осы Сиқырлы пропорцияға негізделіп жаратылғанбыз. Оны мынадан көруге болады, әрбір адам өз денесінің биіктігінің ұзындығын кіндігінен табанына дейінгі ұзындыққа бөлуіне немесе иықтан саусақтарының ұшына дейінгі ұзындыққа бөліп тексеруге болады. 4,10, 5,91

Сурет 1.
(Дереккөзі: https:avtoforex.ru)

Фибоначчи сандарының қасиеттері
1 - қасиеті.
Фибоначчидің алғашқы n- санының қосындысы:
u1+u2+...+un=un+2 -1. (5)
Дәлелдеуі: (4) формуланы пайдаланып келесі формулаларды алып, тізбектей қоссақ:
u1= u3- u2=1u2= u4- u3=1u3= u5- u4 ... ... ... ... ... ... un-1= un+1- unun= un+2- un+1 u1+u2+ ... + un= un+2- u2 ⇨ u1+u2+ ...+ un= un+2- 1
түріндегі қосындыны аламыз. Қасиет толығымен дәлелденді.
2 - қасиеті.
Фибоначчидің тақ нөмірлі сандарының қосындысы:
u1+u3+u5+...+u2n-1=u2n. (6)
Дәлелдеуі: (3) формуланы пайдаланып келесі формулаларды алып, тізбектей қоссақ:
u1= u2u4= u3+ u2 ⇨ u3= u4- u2 u6= u5+ u4 ⇨ u5= u6- u4 ... ... ... ... ... ... u2n-2= u2n+3+ u2n-4 ⇨ ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.