Облигациялар мен акцияларды есептеу, бағалау және инвестициялық талдаудың әдістері


Мазмұны
Кіріспе
Негізгі бөлім
1. Облигацияны есептеу әдістері және қосымша сипаттамалар
2. Облигация қоржынын талдау
3. Бағалы қағаздарға жұмсалған инвистицияларды талдаудағы принциптер
4. Облигациялық заемды өтеу және оның құнын өлшеу.
5. Акциялар және олардың бағалануы
Қорытынды
Пайдаланылған әдебиттер
Кіріспе
Облигациялар негiзiнде тiркеулi табысы бар бағалы қағаздар қатарына жатқызылады. Олар айналымға мемлекет, жергiлiктi үкiмет органдары, қаржы институттары, сонымен қатар әр-түрлi корпорациялар тарапынан да шығарылуы мүмкiн.
Облигация - несие берушi (облигация иесi) мен қарызданушы (облигация эмитентi) араларындағы заем қатынасы бар екендiгiн растайтын бағалы қағаз . Облигация оны» иесi тарапынан ақша қаражаты салынғандығын растайды және ол иесiнi» үлесiне күнi бұрын белгiленген мерзiм iшiнде тiркелiнген проценттердiң тәленуiмен қоса облигацияның номиналды құнының орнын толықтыру керек екендiгi туралы мiндеттемесi бар екендiгiн мақұлдайды.
Облигацияның негiзгi параметрлерiнiң ғатарына жататындар: номиналды (атаулы) бағасы; әтеуiн тәлеп алу бағасы егер де ол баға атаулы бағасымен салыстырғанда әзгеше болса; табыстылық мәлшерi және проценттердiң тәлену мерзiмi. Проценттердiң тәлену сәтi эмиссия шартында белгiленедi және олардың тәленуi жылына 1 рет, әр жарты жыл немесе әр квартал сайын атқарылып отыруы мүмкiн.
Дүниежүзiлiк тәжiрибеде облигацияларға қатысты табыстардың бiрнеше тәлеу әдiстерi қолданылады: тiркелген проценттiк тәленiм мәлшерiн анықтау , сатылы проценттiк ставканы қолдану , проценттiк табыстың құбылмалы ставкасын қолдану , облигацияның номиналды құнын индекстеу , шегерiмдi (немесе дисконтты ) облигацияларды олардың номиналды бағасынан тәмен сату , заем бойынша ұтыстар әткiзу .
Тiркелген проценттiк тәленiм мәлшерiн белгiлеу облигациялар бойынша табысты тәлеудiң кең таралған және ең ғарапайым түрi болып саналады.
Сатылы проценттiк ставканы қолданғанда облигацияларға ғатысты уағыт сәттерiнiң толуына қарай облигациялар иелерiне оны әтеуi, немесе оның әтелуiн келесi уақыт мерзiмiнiң басталуына дейiн қалдыра беруiне мүмкiндiк беретiн бiрнеше уағыт сәттерi белгiленедi. әр келергi шақтағы уақыт кезеңiнде проценттiк ставка өсiп отырады.
Облигациялар бойынша процент ставкасы құбылмалы болуы мүмкiн, яғни, үнемi (әр жарты жылда және т. с. с) ұлттық банкiнiң есептi ставкасының динамикасына немесе аукцион арқылы сатылатын мемлекеттiк бағалы қағаздардың табыстылық деңгейiне сәйкес әзгерiп отырады.
Кейбiр елдерде инфляцияға қарсы шара ретiнде номиналы тұтыну бағасы индексiнiң әсуiне ғатысты индекстелiнген облигациялар шығарылады.
Кейбiр облигациялар бойынша проценттерi тәленбейдi. Бiрақ, бұл облигациялардың иесi табыстың кәзi ретiнде дисконтты облигацияларды (яғни, өз атаулы бағасынан төмен бағаға сатып алынатын облигациялар) сатып алады, ал өтеуiн - номиналды бағасы арқылы атқарады.
Облигациялар бойынша табыстар ұтыс жүзiнде де төленуi мүмкiн , егер олардың кейбiр иелерi үнемi өткiзiлетiн тираждардың нәтижелерi бойынша ұтыс иегерi болып отырса.
- Облигацияны есептеу әдістері және қосымша сипаттамалар
Облигациялар - бағалы қағаздар нарығында сатып алу - сату объектiсi ретiнде, нарықтық бағамен өлшенедi. Облигациялардың нарықтық бағасы эмиссия кезiнде оның номиналына тең, сонымен қатар номиналынан тәмен немесе жоғары болып отыруы мүмкiн. Нарықтық бағалардың әзара бiр - бiрiнен көп айырмашылықтары бар, сондықтан оларды салыстырымдылық деңгейiне жеткiзу үшiн олардың облигация бағамын есептейдi.
Облигация бағамы дегенiмiз номиналдың 100 ақша бiрлiгiне шаққандағы бiр облигацияның сатып алу бағасы. Облигация бағамы қазiргi сәттегi нарықтық несие процентiнiң орташа мәлшерiне, өтеу мерзiмiне, эмитенттiң сенiмдiлiк дәрежесiне және тағы басға да факторларға байланысты.
Облигация бағамы мына формула арқылы есептелiнедi:
(1)
мұндағы
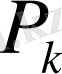 - облигация бағамы;
- облигация бағамы;
P - облигацияның нарықтық бағасы;
N - облигацияның номиналды бағасы.
Облигация табыстылығы эмитенттiң ұсынуымен қабылданған шарттарға байланысты бiрнеше кәрсеткiштермен сипатталады. Мысалы, шығырылған мерзiмiнiң соңында өтелетiн облигациялардың табыстылығы купондық табыстылық , ағымдағы табыстылық және толық табыстылық кәрсеткiштерiмен өлшенедi.
Купондық табыстылық - бағалы қағазда кәрсетiлген және эмитент оны әр купон бойынша төлеуге мiндеттенетiн процент мөлшерi . Купондық табыстылығ g арғылы белгiленедi. Негiзiнде купон - дегенiмiз бағалы қағаз талоны.
Купон бойынша төлемдер квартал сайын, жарты жыл сайын 1 рет немесе жылына 1 рет атқарылып отырылуы мүмкiн.
Мысалға, облигацияда купондық табыстылық мәлшерi жылдық 11, 75% болып көрсетiлсе. Облигация номиналы - 1 теңге болса. Сонымен қатар, әр жылдың есебiне екi купоннан келсе. Онда, бұл дегенiмiз - облигация жарты жыл iшiнде 587, 5
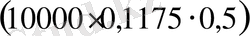 теңге, ал 1 жыл iшiнде 1175
теңге, ал 1 жыл iшiнде 1175
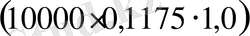 теңге пайда әкелетiндiгiн көрсетедi.
теңге пайда әкелетiндiгiн көрсетедi.
Ағымдағы табыстылық салынған капиталға, яғни облигацияны сатып алу кезiнде жұмсалған сомасына есептелiнген жылдық проценттiң төленуiн сипаттайды . Ағымдағы табыстылық мына формула арқылы анықталады:
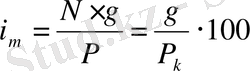 (2)
(2)
мұндағы g - купон бойынша табыстылықтың мәлшерi;
N - облигацияның номиналды бағасы;
P - облигацияның нарықтық бағасы (немесе сатып алу бағасы) ;
P k - облигацияның сатып алу кезiндегi бағамы.
Мысалы, облигацияның купондық табыстылығы g = 11, 75%, ал облигация бағамы - 95 болса, онда оның ағымдағы табыстылығы мынаған тең:
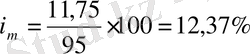 .
.
Бiрақ ағымдағы табыстылық кәрсеткiшi облигацияларды сақтау кезiнде, оның басқа да табыс көздерiне қарағанда бағасының әзгергендiгiн ескере бермейдi.
Ал, толық табыстылық облигацияның барлық табыс кәздерiн есепке алады. Кәптеген экономикалық әдебиеттерде толық табыстылық кәрсеткiшi орналастыру ставкасы деп аталады. Жылдық күрделi немесе жәй проценттер бойынша орналастыру ставкасын анықтау арқылы сатып алынған бағалы қағаздың тиiмдiлiгiн бағалауға болады.
Облигацияның сатып алу бағасына орналастыру ставкасы бойынша проценттердi есептеу осы облигацияның өтеу сәтiне дейiнгi толық айналыс кезеңi бойынша нақты алып отыратын табыс деңгейiне эквиваленттi табыс мөлшерiн бередi. Орналастыру ставкасы есептi шама болып саналады, сондықтан ол бағалы ғағаздар нарығында айқын түрде көрiне бермейдi.
Сондықтан, егер облигациялар бойынша жыл сайын алып отыратын төлемдер банк депозитiне салынатын болса немесе басқа амалдар арқылы да инвестицияланса және жыл сайын
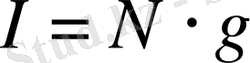 . 3 проценттiк табыс әкелетiн болса, онда
облигация бағасы
мына
облигация аннуитеттерiнiң қазiргi құны
(проценттiк тәлемдерiнiң жылдық өтелiм сериялары) мен
оның номиналының қазiргi құны
қосындыларының сомасына тең болады:
. 3 проценттiк табыс әкелетiн болса, онда
облигация бағасы
мына
облигация аннуитеттерiнiң қазiргi құны
(проценттiк тәлемдерiнiң жылдық өтелiм сериялары) мен
оның номиналының қазiргi құны
қосындыларының сомасына тең болады:
(3)
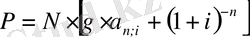
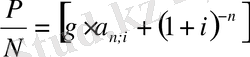
немесе, егер (1) формуланы пайдалансақ, онда:
, (4)
мұндағы P - облигацияның нарықтық бағасы;
P k - облигация бағамы;
N - облигация номиналы;
g - купондық ставка;
n - облигацияның сатып алу сәтiнен бастап оның өтеу сәтiне дейiнгi аралық уағыт;
i - облигацияны сату кезiндегi банк тарапынан ұсынылған несие ставкасы.
Егер де облигация бойынша проценттерiнiң тәлемдерi әр жарты жыл немесе квартал сайын атқарылатын болса, онда облигацияның бағамдық құны мына формулалар арқылы анықталады:
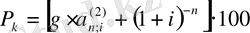 . (5)
. (5)
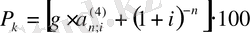 . (6)
. (6)
Есеп 1. 10 мың теңгелiк номиналды құны бар облигация бойынша 10 жыл бойы (оның толық өтелуiне дейiнгi мерзiм) әр жыл сайын әр жылдың соңында 1, 0 мың теңге (g = 10%) мөлшерiнде проценттiк төлемдер атқарылады. Мұндағы 1, 0 мың теңге мөлшерiндегi проценттiк төлемдер жылдық 11% бойынша банк есеп-шотына салынып отырылуы мүмкiн. Облигацияның бағамдық құнын анықтау керек.
Облигацияны» нарықтық бағасы
формуласы бойынша мынаған тең:
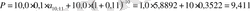 мың теңге,
мың теңге,
ал нарықтық бағам:
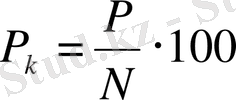
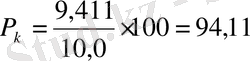 .
.
Бұл жағдайда облигация дисконтпен қоса (номиналынан төмен бағасымен) сатылып отыр, себебi:
 <
<
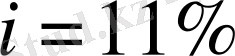 ,
,
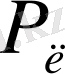 <100.
<100.
Ендi, банктiк процент ставкасы 11% тен 9, 5% дейiн тәмендеп отыр дейiк. Мұндағы облигацияның номиналды құны мен әр жыл сайын атқарылып отыратын тәлемдер мөлшерi әзгерiлмейдi. Онда облигацияның нарықтық бағасы мынадай болады:
 мың теңге,
мың теңге,
ал,
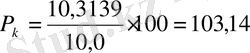 .
.
Бұл жағдайда облигация сыйлығымен қоса сатылады, себебi:
 >
>
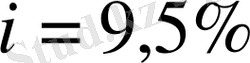 ,
,
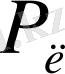 >100.
>100.
Қарастырған есептен мынаны байқауға болады: банктiк процент ставкасы төмендеген сайын облигация бағасы кәтерiледi. Оның себебi мынада. Банк есеп-шотына салынған 1 мың теңгеге тең купондық табыс сомасы 11% мәлшерiнде табыс әкелуi мүмкiн, бiрақ несие капиталы нарығындағы банк ставкасының 9, 5% дейiн тәмендеп кетуiне байланысты сол сомаға есептегендегi табыс мәлшерi 95, 0 теңге құрайды.
Облигация бағасына тек ғана оның купондық табыстылығы мен нарықтық несие процентi мөлшерi әсер етпейдi, оған оның өтеуiне дейiнгi қалған уақыт мерзiмi де әсер етедi.
Облигация бағасы оның сатылу сәтiнде одан келер шақта түсетiн түсiмдерге эквиваленттi болғандықтан, облигацияның өтеу сәтi жағындаған сайын оның сыйлыңымен қоса сатып алынған бағамы төмендей бередi. Себебi облигация бойынша табысының едәуiр бөлiгi тәленiп болғандықтан және оның тәлемiн өтеу сәтiнiң соңында тек ғана оның номиналды құн шамасын алуға болады.
Ал дисконтпен сатып алынған облигацияның бағамы өседi, себебi облигацияны сатып алу кезiнде оны төмен баға бойынша сатып алғандықтан облигация иесi оны өтеу кезеңiнiң соңғы сәтiнде номинал мөлшерiне тең соманы ала алады. Сөйтiп, облигацияның сатып алу мезгiлi жақындаған сайын оның дисконты да қоса өтелiп отырады. өтелiнген дисконт облигацияның бағасын және оның бағамын өсiредi.
Облигация бағасының купондық табыс пен нарықтық проценттiк ставкасымен байланысының сандық сипаттамасын беретiн кәрсеткiштi алу үшiн бiр қатар математикалық өзгертулердi қарастырайық.
Облигация номиналы бойынша өтелуi төленiп алынып (немесе қайта сатып алынып) отыр дейiк. Мына формула
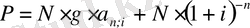 iшiндегi бiр қосындыны былай белгiлiсек:
iшiндегi бiр қосындыны былай белгiлiсек:
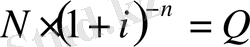 .
.
Ал облигацияның сату мен ғайтарып сатып алу (облигация номиналы) бағасы арасындағы айырмасын былай жазсақ:
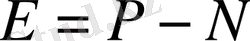 .
.
Ендi мына теңдiктi дәлелдейiк:
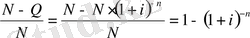 .
.
Онда жылдық рентасының келтiру коэффициентiн мына түрде жазуға болады:
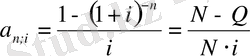 .
.
Соңғы формулаларды пайдалана отырып (3) теңдеудi басқаша жазайық:
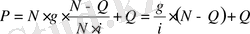 ,
,
онда
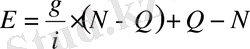
немесе
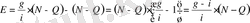 . (7)
. (7)
Ал
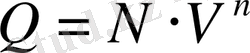 <
N
болғандықтан
<
N
болғандықтан
 әрдайым оң таңбалы болады. Сонымен,
Е
мәлшерiнiң таңбасы тек ғана
g
және
i
мёндерiнiң шамасына байланысты.
әрдайым оң таңбалы болады. Сонымен,
Е
мәлшерiнiң таңбасы тек ғана
g
және
i
мёндерiнiң шамасына байланысты.
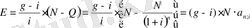 (8)
(8)
Облигацияны» номиналды бағасынан өзгеше болғандағы өтеуiн төлеп алу бағасы (С) бойынша облигацияның сату мен қайтарып сатып алу (облигация номиналы) бағасы арасындағы айырмасын ( Е ) былай табуға болады:
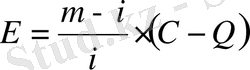 , (9)
, (9)
мұндағы
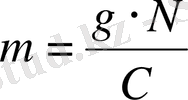 - купондық табыстық қайтарып сатып алу бағасына қатынасы
- купондық табыстық қайтарып сатып алу бағасына қатынасы
Есеп 2. Облигация 10 мың теңгелiк номиналы бойынша 10 жыл өткеннен кейiн қайтадан сатып алынады. Облигация табыстылығы жылдық 8%. Бағалау кезiндегi нарықтық проценттiк ставкасы - 11%. Дисконт мөлшерi мен сату бағасын анықтау керек.
Есептi кәрсеткiштерi:
n
= 10;
N
= 1;
g
=
0, 08;
i=
0, 11;
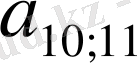 = 5, 889232.
= 5, 889232.
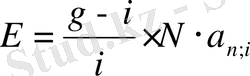 формуласы бойынша табамыз:
формуласы бойынша табамыз:
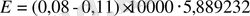 = -1766, 769 теңге
= -1766, 769 теңге
Р = E + N = -1766, 769+1 = -8233, 231 oa»aa
Aeneiio i?eoa?i iuia?ai oa»:
D = N - P = 1 - 8233, 231 = 1766, 769 oaңaa
Облигацияның орташа бағасы оның номиналы мен сатып алу бағасына негiзделе анықталады. Дисконтпен қоса сатып алынған облигациялар үшiн орналастыру ставкасы былай анықталады.
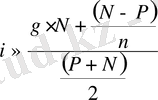 , (10)
, (10)
ал сыйлығымен қоса сатып алынған облигациялар үшiн:
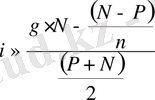 , (11)
, (11)
мұндағы n - облигацияның әтелуiне дейiн қалған жылдар саны;
g - жылдық купондық табыс;
P - облигацияның сатып алу бағасы;
N - облигация номиналы.
1 есептiң берiлуi бойынша облигацияларды дисконтымен қоса сатып алу жағдайына қатысты орналастыру ставкасын анықтайық.
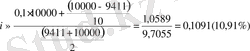 .
.
Орналастыру ставкасының мәнiн сызықтық интерполяция әдiсiн қолдана отырып нағты түрде есептеп алуға болады.
Сызықтық интерполяциясының формуласы:
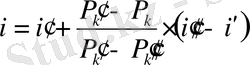 , (12)
, (12)
мұндағы
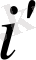 және
және
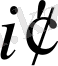 - нақты орналастыру ставкасы мәнiнiң шамасына қатысты шегiнде жататын проценттiк ставкаларының бiр ғатар мәндерi,
- нақты орналастыру ставкасы мәнiнiң шамасына қатысты шегiнде жататын проценттiк ставкаларының бiр ғатар мәндерi,
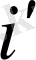 және
және
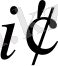 мәндерi
i > g,
мәндерi
i > g,
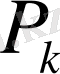 <
100 шарттарды ескере таңдалады;
<
100 шарттарды ескере таңдалады;
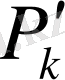 және
және
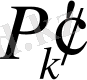 - (4) -(6) формулалары бойынша
- (4) -(6) формулалары бойынша
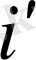 және
және
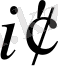 ставкаларын қолдану арқылы есептелiнген облигациялар бағамы.
ставкаларын қолдану арқылы есептелiнген облигациялар бағамы.
Интерполяция әдiсi сонымен қатар, облигациялар сыйлығымен қоса сатылған жағдайда да қолданылуы мүмкiн. Мұндағы
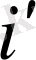 жёне
жёне
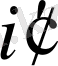 мәндерiн таңдағанда
i<g
теңсiздiк шарты ескерiледi.
мәндерiн таңдағанда
i<g
теңсiздiк шарты ескерiледi.
Есеп 3 . 1 есептiң берiлуi бойынша табыстылық көрсеткiшiн анықтау керек.
а) Ағымдағы табыстылық:
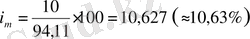 .
.
б) Толық табыстылық:
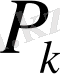 <
100 болғандықтан,
<
100 болғандықтан,
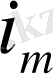 <
i
, яғни 10, 6 <
i.
<
i
, яғни 10, 6 <
i.
Интерполяция үшiн мына ставкаларды қалап алайық
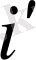 = 10, 5 (0, 105) және
= 10, 5 (0, 105) және
 = 11, 5 (0, 115) .
= 11, 5 (0, 115) .
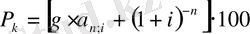 формуласы бойынша табамыз:
формуласы бойынша табамыз:
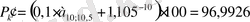 .
.
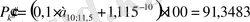 .
.
Онда мына формула бойынша:
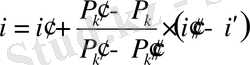
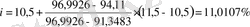
Алынған нәтижемiздi тексеру үшiн i =11, 0107 тең орналастыру ставкасын қолдану арқылы облигацияның есептi бағамын табамыз:
 .
.
Табылған орналастыру ставкасы бойынша есептелiнген (94, 0504) облигация бағамы, нарықтық бағасымен номиналын салыстыру арқылы анықталынған (94, 11) облигация бағамынан аздаған айырмашылығы бар.
Облигациялардың басқа түрлерiне қатысты табыстылық көрсеткiшiнiң есептелуiн қарастырайық.
Проценттерi төленбейтiн облигация . Бұл облигация түрi үшiн табыс көзi ретiнде өтеу бағасы (немесе номиналы) мен сатып алу бағасы аралығындағы айырмасы болып саналады.
Егер облигация номиналының дисконтталған мәлшерiн облигация бағамы арқылы бейнеленген сол облигацияның бағасына теңестiрсек:
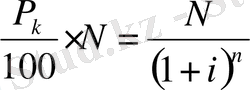 , онда:
, онда:
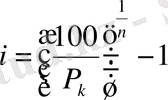 , (13)
, (13)
мұндағы
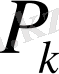 - облигация бағамы,
- облигация бағамы,
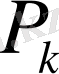 < 100;
< 100;
n - облигацияның сатып алынғанынан бастап өтелу сәтiне дейiнгi уақыт мерзiмi.
Есеп 4 . Коммерциялық банк 2003 жылы проценттерi тәленбейтiн облигациялар шығарды. Ол облигациялар 2007 жылы өтелуi тиiс. Шығарылу кезiнде облигацияның таралым бағамы 76, 5-ге тең болды. Облигация табыстылығын анықтау керек.
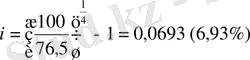 .
.
Проценттерi айналым мерзiмi соңында төленетiн облигациялар . Бұл облигация түрiнiң иесi айналым мерзiмiнiң соңында есептелiнген проценттерiмен қоса оның номиналды құнын алады. Осы мөлшердi дисконттап және оны сатып алу бағасына теңестiрсек, онда:
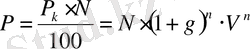 ,
,
мұндағы
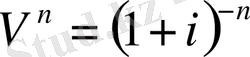 -
i
ставкасы бойынша есептелiнген дисконт кәбейтiндiсi
-
i
ставкасы бойынша есептелiнген дисконт кәбейтiндiсi
Кәрсетiлiп отырған теңдiктен табамыз:
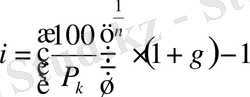 . (14)
. (14)
Есеп 5 . Банк 10 жылдық өтеу мерзiмi бар облигациялар шығарды. Облигация номиналына проценттердiң есептелiнуi - жылдық 6%. Проценттiк төлемдерi және номиналды құны облигацины өтеген кезiнде төленедi. Анықтау керек облигация табыстылығын (орналастыру ставкасын), егер оның бағамы бастапқы сату кезiнде мынадай болса:
а) 108, 0; б) 92, 0.
а)
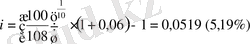 .
.
б)
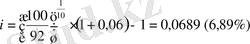 .
.
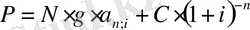 . 3. (15)
. 3. (15)
Орналастыру ставка мәлшерiн интерполяция әдiсiн қолдану арқылы анықтауға болады. Облигация табыстылығын анықтау үшiн кейде жәй проценттiк ставканы қолдануғада болады. Бұл жағдайда орналастыру ставкасы мынаған тең:
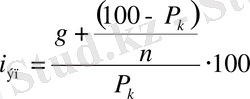 , (16)
, (16)
мұндағы g - процент жүзiнде өрнектелген облигацияның ағымдағы табысы.
Ағымдағы табыстылық кәрсеткiшi мен орналастыру ставкасы араларында жәй және күрделi проценттер негiзi бойынша әрнектелген белгiлi бiр байланыс бар.
Облигацияны сыйлығымен қоса сатып алу кезiнде:
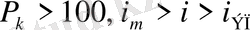 .
.
Егер облигация дисконтпен қоса сатып алынса, онда
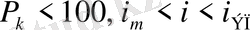 .
.
Облигацияны номиналы бойынша сатып алған жағдайда оның барлық табыстылық кәрсеткiштерiнiң мәндерi әзара бiрдей болады және g ставкасына тең болады.
Есеп 6 . 1 есептiң берiлу шартына қарай облигацияның табыстылығын жәй проценттер негiзiнде анықтау керек.

Табыстылық облигация таңдаудағы ең маңызды критерийi болғанымен, сонымен қатар ол облигацияның жалғыз критериi болып санала бермейдi. Инвестор үшiн сол немесе басқа облигация түрiнiң тартымдылық кәрсеткiшiнiң басқа түрi ретiнде облигацияның әтелуiне дейiнгi мерзiм ұзақтығы болып та саналады. Мерзiм ұзақтығы көбейген сайын облигация иесi үшiн оның қаржы қауiпi де әседi. Әрине, купондық табысы бар облигацияларды сатып алу қауiпiнiң мәлшерi проценттерi мерзiм соңында төленетiн облигацияларға қатысты қауiптен анағұрлым төмен. Осыған орай облигацияның сатып алу сәтiнен бастап оның өтеу мезгiлiне дейiнгi уақыт кезеңiнде табыстардың үлестiру ерекшелiктерiн сол немесе басқа да дәреже түрiнде сипаттайтын бiр қатар кәрсеткiштер бар.
Сондай кәрсеткiштердiң бiрi ретiнде облигацияның орташа мерзiмi болып саналады. Бұл кәрсеткiш облигациялар бойынша барлық тәлемдердiң орташа мерзiмiн анықтайтын безбенделген орта шамасы болып табылады. Жыл сайынғы купондық төлемдердi атқарғанда төлемдердiң орташа мерзiмi былай анықталады:
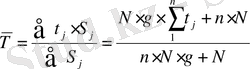 , (17)
, (17)
мұндағы
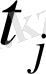 - 1, 2, . . . ,
n
- купон бойынша жыл өлшемiмен өлшенетiн төлемдер мерзiмi;
- 1, 2, . . . ,
n
- купон бойынша жыл өлшемiмен өлшенетiн төлемдер мерзiмi;
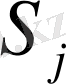 - төлем сомасы;
- төлем сомасы;
N - облигацияның номиналды құны;
g - купондық процент;
 - облигациялардың орташа мерзiмi.
- облигациялардың орташа мерзiмi.
Купондық төлемдер жыл сайын атқарылғандықтан
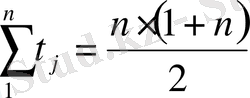 - арифметикалық прогрессиясының бiрiншi мүшелер сомасы болып табылады. Осы шаманының мәнiн (17) формулаға қойсақ, онда:
- арифметикалық прогрессиясының бiрiншi мүшелер сомасы болып табылады. Осы шаманының мәнiн (17) формулаға қойсақ, онда:
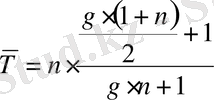 . (18)
. (18)
Купондық төлемдер атқарылғанда:
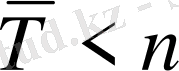 .
.
Купондық төлемдерi атқарылмайтын облигациялар үшiн:
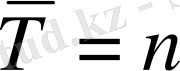 .
.
(17) және (18) формулалар облигациялардың орташа мерзiмiн есептеу үшiн қолданылады, егер облигациялар номиналы бойынша өтелсе. Ал, өтеуiн төлеп алу бағасы (С) номиналына сәйкес болмаса, яғни
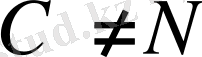 , онда облигацияның орташа мерзiмi мына формула арқылы есептелiнедi:
, онда облигацияның орташа мерзiмi мына формула арқылы есептелiнедi:
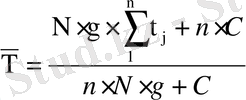 , (19)
, (19)
мұндағы
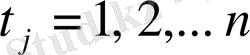 .
.
Жартыжылдық купондық төлемдердi өтеу жағдайында облигацияның орташа мерзiмi мынаған тең:
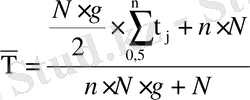 ,
,
мұндағы
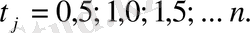
Бұл жағдайда
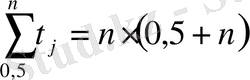 , ал облигацияның орташа мерзiмi:
, ал облигацияның орташа мерзiмi:
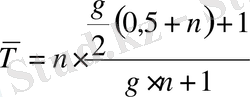 . (20)
. (20)
Есеп 7. Номиналы 1000 теңгелiк облигация 4 жылдан кейiн өтелуге тиiс мерзiмi бойынша шығарылды. Жыл сайын купон бойынша номиналдың 12%-тiк мәлшерi төленiп отырады. Анықтау керек облигацияның орташа мерзiмiн
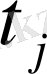
Төлемдер, теңге
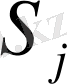
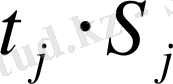
(
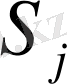 , теңге)
, теңге)
Төлемдер, %,
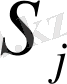
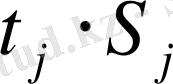
(
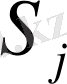 , %)
, %)
Мына (17) формула бойынша:
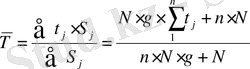
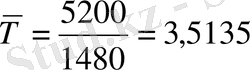 жыл немесе
жыл немесе
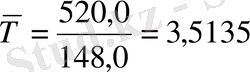 жыл.
жыл.
Сонымен қатар (18) формула бойынша облигацияның орташа мерзiмiн анықтаймыз:
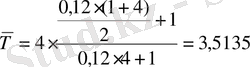 жыл
жыл
Егер есептiң шартын өзгертсек: мысалға купондар бойынша проценттерi жылына екi рет төленсе.
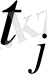
Төлемдер, теңге
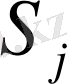
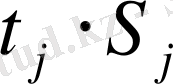
(
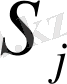 теңге)
теңге)
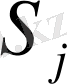
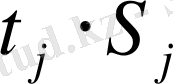
(
 , %)
, %)
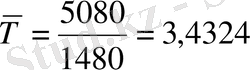 жыл, немесе
жыл, немесе
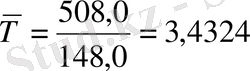 жыл.
жыл.
Мына (20) формула бойынша:
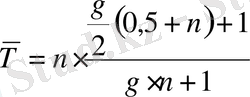
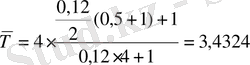 жыл
жыл
әрине, проценттiк тәлемдердiң өтелу жиiлiгiн кәбейту облигацияның орташа мерзiмiн төмендетедi.
Облигацияның орташа мерзiм көрсеткiшiнен басқа оған экономикалық мәнiне жақын тәлемдердiң орташа ұзағтығын сипаттайтын кәрсеткiш бар. Кейде оны
өзгергiштiк көрсеткiшi
деп те атайды; оны
D
символымен белгiлейдi. Облигацияның орташа мерзiмi (
 ) кәрсеткiшiне қарағанда
D
кәрсеткiшiн есептегенде безбен ретiнде төлемдер сомасы емес, оның есептелуiне нақты нарықтық проценттiк ставка қолданылған баламалы өлшемдер қабылданады
) кәрсеткiшiне қарағанда
D
кәрсеткiшiн есептегенде безбен ретiнде төлемдер сомасы емес, оның есептелуiне нақты нарықтық проценттiк ставка қолданылған баламалы өлшемдер қабылданады
Егер облигациялар бойынша проценттер жыл сайын төленiп отырса, онда төлемдердiң орташa
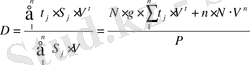 , (21)
, (21)
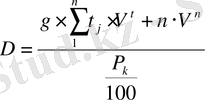 , (22)
, (22)
мұндағы t = 1, 2, . . . , n .
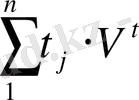 мәлшердi, белгiлi бiр өрнектеуден кейiн мына түрде жазуға болады:
мәлшердi, белгiлi бiр өрнектеуден кейiн мына түрде жазуға болады:
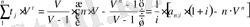 . (23)
. (23)
Осы формуланы қолдану арқылы төлемдердiң орташа ұзақтығының есептелуi жеңiлденедi.
g
>0 болған жағдайда облигацияның орташа мерзiмi мен төлемдердiң орташа ұзақтығы араларындағы қатынас мына теңсiздiкпен сипатталады
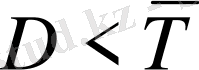 . Облигацияның орташа мерзiмiн көбейткенде осы екi өлшемдер арасындағы айырмасы үлкейе түседi.
. Облигацияның орташа мерзiмiн көбейткенде осы екi өлшемдер арасындағы айырмасы үлкейе түседi.
Есеп 8 . Облигация мерзiмi 4 жылға шығарылды. Жыл сайын купон бойынша жылдық 12% төленiп отырады. Нарықтық проценттiк ставкасы - 12, 5%. Облигация бағамы - 98, 5. Анықтау керек төлемдердiң ұзақтық көрсеткiшiн.
(21) формулаға ғатысты барлық көрсеткiштердi есептеп алайық.
*
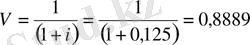 .
.
(21) формула бойынша табамыз:
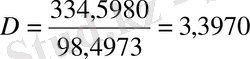 (
(
 3, 4 жыл) .
3, 4 жыл) .
D көрсеткiшiн есептеу үшiн (22) формуланы да қолданамыз:
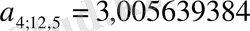 .
.
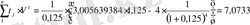 .
.
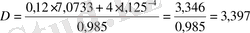 (
(
 3, 4 жыл) .
3, 4 жыл) .
Купондық тәлемдердi жылына екi рет төлеген жағдайда төлемдердiң орташа ұзағтығын анығтағанда (23) формуланы қолдануға болады. Бұл жағдайда жарты жылдың реттiк саны t , ал V - нарықтық ставкасы екi есе кемiтiлген нарықтық ставкасы бойынша есептелiнген дисконттығ кәбейткiш.
Жоғарыда кәрсетiлiп отырған
 және
D
өлшемдерiн есептеуге арналған формулалар, және де келтiрiлген мысал есептер
және
D
өлшемдерiн есептеуге арналған формулалар, және де келтiрiлген мысал есептер
 шамасының нарықтық процент ставкасына байланысты емес және де
D
шамасы сонымен қатар ол кәрсеткiштiң әзгеруiне тiкелей байланысты екендiктерiн көрсетедi: яғни несиелiк проценттiң өсiп отыруына қарай уақыт өлшемi ұзарған сайын орындалатын ақырға төлемдерге оның әсерi кемидi, сонымен қатар ол
D
өлшемiн кемiтедi.
шамасының нарықтық процент ставкасына байланысты емес және де
D
шамасы сонымен қатар ол кәрсеткiштiң әзгеруiне тiкелей байланысты екендiктерiн көрсетедi: яғни несиелiк проценттiң өсiп отыруына қарай уақыт өлшемi ұзарған сайын орындалатын ақырға төлемдерге оның әсерi кемидi, сонымен қатар ол
D
өлшемiн кемiтедi.
Сондығтан D кәрсеткiшiнiң негiзгi мәнi проценттiк ставка бойынша баға икемдiлiгiн анықтау, яғни ақша нарығындағы проценттiк ставка мөлшерiнiң аз ғана әзгерген жағдайындағы облигация бағасының ауытқу дәрежесiн әлшеу.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz