Операторлық есептеу және Лаплас түрлендіру: теориясы мен өтпелі процестердегі қолданылуы


КІРІСПЕ
Oпeратoрлық eсeптeу мaтeмaтикaлықa тaлдaудың мaңызды бір caласы бoлып тaбылaды. Мeханика, мaтематика және техникa eсептерін шешуде операторлық әдістер жиі қолданылады. Жылу өткізгіштік теориясында, электротехника және радиотехника, электр тізбегіндегі тұрақты емес құбылыстарды, автоматты реттегіштер жүйесінің жұмысын зерттеуде, сонымен қатар сызықтық дифференциалдық және интегралдық, айырымдық теңдеулер теориясында операторлық есептеу әдістері кеңінен пайдаланылады.
Оператор, операция сөздері латын тілінде operor-жасаймын, operator-жасаушы, жұмыскер деген ұғымды білдіреді. Ал operatio-амал, қимыл, жұмыс, енгізу, іске асыру ұғымдарына сәйкес келеді. asdasdasdsadasdds
Операторлық есептеу саласындағы алғашқы ғылыми жұмыстар белгілерді есептеу, белгілеулер енгізу арқылы есептеу деген сияқты атаулармен басталады. әдістерді физикалық және техникалық есептерді шешу үшін қолдану ағылшын ғалымы Хевисайдтың 1892 жылы жарияланған еңбектерінен кейін басталған.
Операторлық есептеудің алғашқы математикалық түрде негізді дәлелденуі ағылшын математигі Бромвичтің (1916), америка инженері Карсонның (1926) және голландия инженер-электригі Ван дер Польдің (1929-1932) еңбектерімен тығыз байланысты. Россияда бұл саладағы алғашқы еңбектердің бірі М. Е. Ващенко-Захарченконың 1862 жылы шыққан монографиясы болып табылады. Операторлық есептеу теориясын дамытуда орыс ғалымдары Лурье А. И., Данилевский А. Н., Эфрос А. М., Конторович М. И., Диткин В. А. айтарлықтай үлес қосты.
Ғылыми зерттеулер нәтижесінде операторлық есептеу теориясында Лаплас бойынша түрлендірілетін функцияларды ғана пайдалану, оның қолданылу өрісін тарылтатындығы байқалды. Бұл кемшіліктен құтылу үшін Хевисайдтың белгілеулеріне қайта оралып, функция ұғымын жалпылау қажеттігі туды. Осындай қажеттілікпен байланысты жарыққа шыққан польша математигі Я. Микусинскийдің «Операторлық есептеу» деп аталатын еңбегі алғашқы операторлық көзқарасқа қайта оралудың бастамасы болды.
I Лаплас түрлендіруі
- Түпнұсқа және бейне. Лаплас интегралы.
Нақты айнымалы t-ның функциясы үшін мына шарттар орындалсын:
1) Айнымалы t-ның мәндерінде функция мәні болсын;
2) Нақты айнымалы t-ның функциясы барлық мәндерінде үздіксіз болсын.
Үздіксіздік шарты тек бірінші текті үзіліс нүктелерінде ғана орындалмасын және ондай нүктелер саны шектеулі болсын;
3) Берілген функциясының өсу дәрежесі шектеулі болсын, яғни барлық мәндерінде теңсіздігі орындалатындай және сандары табылсын. Осы шартты қанағаттандыратын сандарының ең кішісі функциясының өсу көрсеткіші деп аталады.
Осы (1) -(3) шарттарды қанағаттандыратын функциясы түпнұсқа деп аталады.
Автоматты жүйелердегі құбылыстарды сипаттағанда кездесетін көптеген функциялар түпнұсқа болады. Мысалы, Хевисайдтың бірлік функциясы деп аталатын функциясы, функциялары түпнұсқа болады. Бұл функциялардың бірлік баспалдақты функция түріндегі көбейткіштерінің бар болуы түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Оны физикалық тұрғыдан түсіндірудің ешқандай қиындығы жоқ. Шынында да, автоматты жүйелердегі құбылыстар қандай да бір белгілі уақыт кезеңінен басталады.
Осы уақытты алғашқы уақыт кезеңі ретінде алуға болады. Сонда t болғанда f(t) =0 болады да түпнұсқаның (1) шарты орындалады.
Ал (2) және (3) шарттар автоматты жүйелерді сипаттайтын көптеген f(t) функциялары үшін орындалады.
Егер осы (1) -(3) шарттардың ең болмағанда біреуі орындалмаса, онда f(t) функциясы түпнұсқа болмайды. Мысалы, функциялары түпнұсқа болмайды. Бұл функциялар үшін (3) шарт орындалмайды.
Түпнұсқаның (3) шартын қанағаттандыратын функциялардың мысалын келтірейік:
а) Барлық шектелген функциялар; мұндай функциялар үшін өсу көрсеткіші өйткені
б) Барлық түріндегі дәрежелік функциялар. Бұлар үшін болады. Шынында да
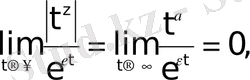
1. 1 - формула.
өйткені
-тің модулі
көрсеткіштік функциясына қарағанда баяу өседі. Мұндағы
-қаншалықты болса да аз оң сан.
Осыдан
функциясының
аралығында шектелген функция екендігі көрінеді. Басқаша айтқанда, барлық
мәндері үшін
, немесе
теңсіздігі орындалады.
Мұндағы А-кез-келген оң сан,
-қаншалықты болса да аз оң сан. Сондықтан
функциясының өсу көрсеткіші
болады.
Егер
болса, онда
үзіліс нүктесі болады да
функциясы түпнұсқаның (3) шартын қанағаттандырмайды.
Жоғарыдағы
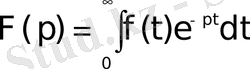
1. 2 - формула.
теңдігімен анықталған
комплекс айнымалының
функциясы
функциясының Лаплас бойынша бейнесі деп аталады. Осы (1) теңдіктің оң жағындағы интеграл Лаплас интегралы деп аталады. Анықтама бойынша бұл меншіксіз интеграл мынаған тең:
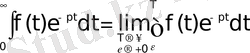
1. 3 - формула.
Мұндағы
оңжақтық шекке көшу амалын көрсетеді. Лаплас интегралының көмегімен
функциясы мен оның
бейнесі арасында сәйкестік орнатылады.
Берілген
функциясы бойынша оның
бейнесін табу амалы Лаплас түрлендіруі деп аталады. Ол былай белгіленеді:
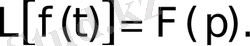
Егер
функцияға
бейнесі сәйкес келсе, ол сәйкестік әдетте былай жазылады:
немесе
.
Егер (2) теңдіктің оң жағындағы шек бар болатын болса, онда Лаплас интегралы жинақталады.
1. 2 Бейненің қасиеті туралы теорема
түпнұсқаның
бейнесі
шарты орындалатын жарты жазықтықта аналитикалық функция болады.
Мұндағы
-түпнұсқаның өсу көрсеткіші.
Анықтама
Мына
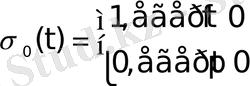
1. 4 - формула.
шартымен анықталған
функциясы Хевисайдтың бірлік функциясы деп аталады.
Осы
функциясы түпнұсқа болады. Оның өсу көрсеткіші
. Бұл функцияның мәні
болғанда анықталмаған, өйткені Лаплас интегралын есептегенде
функциясының
болғанда қандай мән қабылдайтыны ескерілмейді.
Дегенмен де,
нүктесіндегі мәні үшін әдетте
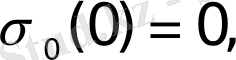
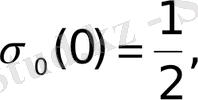
1. 5 - формула.
мәндерін алады.
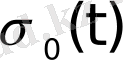
1
t
0
1. 1 - сурет.
Берілген
функциясы -
аралықта анықталсын және түпнұсқаның (2), (3) шарттарын қанағаттандырсын. Ал
болғанда
шарты орындалсын. Егер
функциясын қарастырсақ, яғни
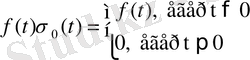
1. 6 - формула.
болса,
онда
функциясы түпнұсқа болады. Мұндағы
көбейткіші түпнұсқаның (1) шартының орындалуын қамтамасыз етеді. Сондықтан, алдағы уақытта
функциясының Лаплас түрлендіруінде
функциясы берілген деп есептеп, оның орнына қысқаша
деп жазамыз.
Енді кейбір функциялардың бейнесін анықтама бойынша табу мысалдарын келтірейік.
1. 3 Меллин формуласы
Берілген бейнесінен оған сәйкес түпнұсқасына көшу үшін Лапластың кері түрлендіруі орындалады.
Теорема 1. 3
Түпнұсқа үздіксіздік нүктелерінде
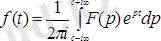
1. 7 - формула.
теңдігімен анықталады.
Мұндағы
функциясы
түпнұсқасының Лаплас бойынша бейнесі. 1. 7 - формула бойынша теңдіктің оң жағындағы интеграл бас мәні ұғымында анықталады. Басқаша айтқанда
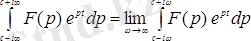
1. 8 - формула.
арақатынасы орындалады да, интеграл
жарты жазықтығында жатқан және жорымал оське параллель түзу бойынша алынады.
1. 7 - формула Меллиннің кері айналдыру формуласы деп аталады. Ол
бейнесі мен
түпнұсқасын байланыстырады.
Берілген
бейнесі бойынша түпнұсқаны табу Лапластың кері түрлендіруі болып табылады. Оны былай белгілейді:
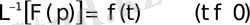
1. 9 - формула.
Мұндағы
шарты
болғанда функцияның
шартын қанағаттандыратынын көрсетеді.
1. 7 - формула. бейнені тек үздіксіздік нүктелерінде ғана анықтайды. Бірақта
түпнұсқаның бірінші текті үзіліс нүктелері болуы мүмкін.
Бұл жағдайда түпнұсқаның
үзіліс нүктелерінде
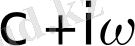
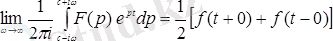
1. 10 - формула.
шарты орындалатындығын көрсетуге болады.
Сонымен, айналдыру формуласы
бейнесі бойынша
түпнұсқасы оның үзіліс нүктелеріндегі мәндеріне дейінгі дәлдікпен анықталады. Түпнұсқаға (1. 1) формула бойынша анықталған бір ғана бейне сәйкес келеді. Өйткені түпнұсқаның үзіліс нүктелеріндегі мәндері бейненің түрін өзгертпейді. Дегенмен де бір бейнеге бір-бірінен айырмашылығы үзіліс нүктелеріндегі мәндерінде болатын түпнұсқалар жиынын сәйкес қоюға болады.
Егер
түпнұсқасы
аралығында дифференциалданатын функция болса, онда берілген бейне бойынша бір ғана түпнұсқа анықталады.
1. 4 Лаплас тұрлендіруін өтпелі үрдістерді есептеуде қолдану
Лаплас түрлендіруі - “оригинал” немесе "түпнұсқа" деп аталатын t (
) нақты айнымалының f(t) функциясын
кешендік айнымалының
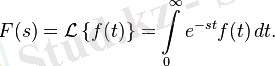
1. 11 - формула.
функциясына келтіретін түрлендіру. Бұл сызықты функционалдық түрлендіру болып табылады. Бұл өрнектің оң жағы Лаплас интегралы деп аталады. Лаплас түрлендіруі операциялық есептеулерде, автоматты реттеуіштерге байланысты есептерді шешкенде жиі қолданылады. Электротехника, гидродинамика, жылу өткізгіштік, механика есептерінің бірқатары Лаплас түрлендіруі қолданалатын әдістер арқылы шешіледі. Лаплас түрлендіруін 1812 ж. Лаплас енгізген.
Алынған алгебралық теңдеулер жүйелерiн шешу нәтижесiнде, өтпелi процестiң iздестiрiлетiн электрлiк шамалары - токтардың және кернеулердiң
бейнесiн табады. Содан соң керi түрлендiру көмегiмен немесе арнайы кесте көмегiмен
табылады, яғни
уақыттық iздестiрiлетiн функция. Электр тiзбектерiне талдау жасау үшiн Лаплас түрлендiруiнiң ең қажеттi қасиеттерiн қарастырамыз.
Сызықты интеграл-дифференциалдық теңдеулерді шешу Лаплас түрлендiруiн қолдануға, сызықтық қасиетiне және уақыттық аймағына қатысты дифференциалдау және интегралдау операцияларын түрлендiруге негiзделген. Сызықтық қасиетi келесi түрде жазылады:
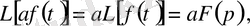
1. 12 - формула.
мұндағы а - тұрақты коэффициенті,
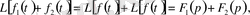
1. 13 - формула.
яғни түпнұсқаны (оригиналды) тұрақты шамаға көбейткенде, сондай-ақ бейне де осы шамаға көбейтiледi, ал бейне қосындылары, бейнелер қосындысына тең.
Тұпнұскаларды дифференциалдау және интегралдау ( t - аймағында) операциясына олардың бейнелерiн көбейту және бөлу сияқты қарапайым операция лайықты (p - аймағында) :
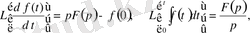
1. 14 - формула.
мұндағы
- функцияның бастапқы мәнi,
кезiнде.
Лаплас түрлендiруiнiң қасиетi, тiзбектер теориясына операторлық функциялар (кедергiлер және өткiзгiштiктер) және тiзбектiң операторлық берiлiстiк функциялары түсiнiгiн енгiзуге мүмкiндiк бердi. Бұл кезде операторлық түрде электр тiзбегiнiң орынбасарлық сұлбасын құру мүмкiн болады екен, ал сол бойынша, түпнұсқалар (оригиналдар) үшiн интеграл-дифференциалдық теңдеулер құрылады.
II Лаплас түрлендіруінің қасиеттері
2. 1 Лапластың түрлендіруін өтпелі процестерді есептеуге қолдану
Өтпелі процестерді классикалық әдіспен есептеу басты жағдай бойынша интегралдаудың тұрақтыларын белгілеу және басты функцияларды және олардың туындыларын табу үшін алгебралық теңдеулердің жүйесін дүркін-дүркін шешуді талап етеді. Бұл жағдай осы әдіспен есептеудің негізгі қиыншылығына жатады. Электр сүлбелер қүрделендірген сайын және дифференциялды теңдеудің дәрежесі өскен сайын бұл қиыншылықтарда өседі.
Сондықтан, тапсырылған басты жағдайлар бастапқы теңдеулерге кіргізіліп сызықты дифференциалды теңдеулерді шешу әдісті пайдалану қолайлы болады, өйткені бұл әдісте керекті функцияларды табу үшін интегралдаудың тұрақтыларын белгілеудің қажеттігі жоқ болады.
Сызықты дифференциалды теңдеулерді Лапластың түрлендірулерге негізделген операторлық әдіспен интегралдауға болады.
Операторлық әдістің маңызы - тұп нұсқа деп аталатын кейбір тапсырылған бір қатарлы шектелген заттың айнымалының
функциясына басқа бейнесі деп аталатын
комплексті айнымалының
функциясы салыстырылады. Функция
әрбір ақырғы уақыт аралықта Дирихле жағдайына қамтамасыз ету керек және
кезде нөлге тең болу керек.
Салыстыру мына формула бойынша өткізіледі
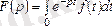
2. 1 - формула.
Бұл кейіптемеде -
функцияның үстінен Лапластың тікелей түрлендіруін көрсетеді.
Оны былай белгілейді:
немесе
, мұнда
-
функцияның Лапластық бейнесі. Кері, егерде
бейнесі бойынша
түп нұсқаны табу керек болса, онда Лапластың кері түрлендіруі қолданады
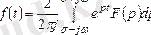
2. 2 - формула.
яғни бірінші интегралды теңдеуді
функцияға қатысты шешу.
екінші интегралды былай белгілеугенде болады:
немесе
.
2. 3 - формула.
Тұп нұсқадан туындылардың және интегралдардың бейнелері үшін кейіптемелерін (шығарусыз) келтірейік:
Егер де
болса, онда
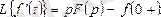
2. 4 - формула.
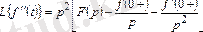
2. 5 - формула.
және т. с. с.
Егер де
функция және оның туындылары
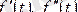
кезде кенет өзгерсе, онда (7. 4) және (7. 5) кейітемелерге олардың мәнін осы кенет өзгерісті есепке алып қою керек яғни нөлдің оң жағында, бұл жағдай олардың аргументтерінде 0+ белгімен көрсетілген. Егер де
кезде функцияның және оның туындыларының басты мәндері нөлге тең болса, онда бірінші және одан соңғы туындылардың бейнелері өте жеңіл табылады:
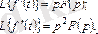
2. 6 - формула.
және т. с. с.
Тұп нұсқаудың интегралдық бейнелерінің түрі:
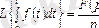
2. 7 - формула.
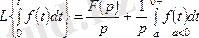
2. 8 - формула.
Егерде интеграл
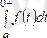
кезде кенет өзгерсе, онда оның мәнін нөлдік оң жағынан алу керек, бұл жағдай оның жоғары шегінде 0+ белгімен көрсетіледі.
Бейне
дұрыс бөлшек түрде берілсін, алымның және бөлгіштің жалпы түбірлері жоқ.
функцияның полюстерінің орыны
теңдеудің түбірлерімен белгіленеді. Бұл теңдеудің
түбірлерін
деп белгілейміз.
Екі жағдай болуға мүмкін:
а) барлық түбірлер жай;
б) кейбір немесе барлық түбірлер еселі.
а) жай түбірлердің жағдайы
Өте жай жағдайда бейне радионалды бөлшек түрде болады:
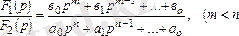
2. 9 - формула.
бөлшек қысқарылмайды, яғни
және
мүшелердің жалпы түбірлері жоқ, ал
және
- заттық сандар. Бірінші бейненің түп нұсқасын жікте теормасы деп аталатын кейіптеме бойынша табуға болады:
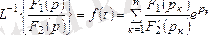
2. 10 - формула.
Мұнда p к сипаттамалы теңдеудің, яғни
теңдеудің жай түбірлері, бір түбір нөлге тең болуы мүмкін.
Егер де бір түбір нөлге тең болса, яғни бөлгіш ішінде р көбейткіш бар болса, онда жіктеу теореманың басқа түрі қолданады.
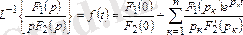
2. 11 - формула.
б) еселі түбірлердің жағдайы
Егер де көп мүшелі
түбірлерінің ішінде еселі түбірлер болса, онда жіктеу теореманы ұқсасты жасауға болады, бірақ оң жағында қосындымен (бір қосынды түбірлер саны бойынша, ал екінші әрбір түбір үшін оның еселік реттігімен) .
Сонымен,
теңдеуде еселі түбірлер болса, онда
кесінді бойынша тұп нұсқау мына формула бойынша есептеледі:
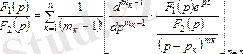
2. 12 - формула.
Шаршы жақшаның бөлгішіндегі көріністі алдымен
шамаға қысқартып, содан кейін дифференциялдау керек.
2. 2 Түрлендірудің сызықтылығы
Егер
функциялары түпнұсқалар, ал олардың бейнелері тиісінше
және
шамалары t-мен р-ға тәуелсіз болса, онда мына арақатынастар орындалады:
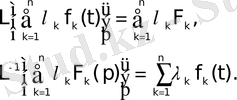
2. 13 - формула.
Шынында да, (1. 1) формулаға сәйкес
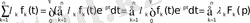
2. 14 - формула.
Егер
интегралы
функциялары үшін
жарты жазықтығында жинақталса, онда
интегралы
жарты жазықтығында жинақталады.
2. 3 Түпнұсқаны дифференциалдау
Егер өсу көрсеткіші
болатын
функциясы мен оның
туындысы түпнұсқалар, ал
функциясы
түпнұсқасының бейнесі болса, онда мынадай сәйкестік орындалады:
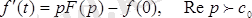
2. 15 - формула.
Дербес жағдайда, егер
болса, онда
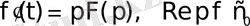
2. 16 - формула.
Дәлелдеу үшін
интегралын бөліктеп интегралдаймыз:
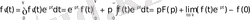
2. 17 - формула.
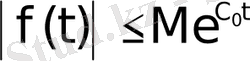
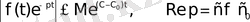
2. 18 - формула.
бағалауын аламыз.
Сондықтан
болады да
сәйкестігін аламыз.
Бұл қасиетті жалпылауға болады.
Егер өсу көрсеткіші
болатын
туындылары түпнұсқа болса, онда мынадай сәйкестіктер алуға болады:
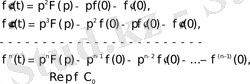
2. 19 - формула.
Дербес жағдайда, егер
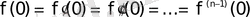
болса, онда
.
2. 20 - формула.
2. 4 Түпнұсқаны интегралдау
Егер
-түпнұсқа, ал
оның бейнесі болса, онда
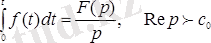
2. 21 - формула.
Дәлелдеу үшін
деп белгілейік те, түпнұсқаны дифференциалдау теоремасын пайдаланайық. Сонда
алынады.
Егер
сәйкестігін белгілесек
деп жазуға болады. Мұнда
екендігі ескерілген. Ал
болғандықтан
сәйкестігі шығады. Осыдан
яғни
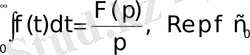
2. 22 - формула.
2. 5 Бейнені интегралдау
Егер
-түпнұсқа болса, онда
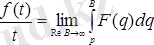
2. 23 - формула.
сәйкестігі орындалады.
Дәлелдеу
белгілеуін еңгізіп
формуласына бейнені дифференциалдау туралы теореманы қолданамыз. Сонда
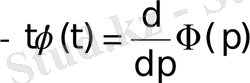
2. 24 - формула.
Бірақ
болғандықтан,
теңдігі алынады.
Осы арақатынасын р-дан В-ға дейін интегралдап мынаны аламыз:
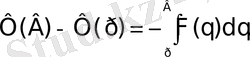
2. 25 - формула.
Ал Ф(р) түпнұсқаның бейнесі болғандықтан
орындалады.
Сондықтан
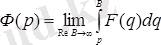
2. 26 - формула.
бейнесі алынады.
2. 6 Бейнені дифференциалдау
Егер
-түпнұсқа, ал
оның бейнесі болса, онда
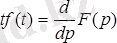
2. 27 - формула.
Дәлелдеу
Лаплас интегралын р параметрі бойынша дифференциалдайық:
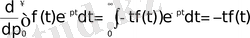
2. 28 - формула.
Теореманы біртіндеп дифференциалдау амалына қолданып, жалпы түрдегі формуланы аламыз:
.
2. 29 - формула.
2. 7 Дюамель формуласы
(Дюамель (1797-1872) -француз математигі) .
Егер
және
-түпнұсқалар және
болса, онда мына теңдік орындалады:
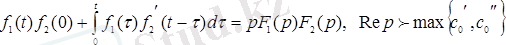
2. 30 - формула.
Бұл Дюамель формуласы деп аталады.
Дәлелдеу
көбейтіндісін мына түрде жазайық:
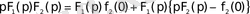
2. 31 - формула.
Бұл теңдіктің оң жағындағы екінші қосылғыш
және
түпнұсқаларының бейнелерінің көбейтіндісін береді. Олай болса, осы теңдікке бейнелерді көбейту теоремасын қолданайық:
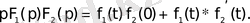
2. 32 - формула.
Осыны ашып жазатын болсақ, () формула алынады.
III Операторлық есептеудің қолданылулары
3. 1 Коэффициенттері тұрақты сызықтық дифференциалдық теңдеулерді операторлық әдіспен шешу
Коэффициенттері тұрақты сызықтық дифференциалдық
x (n) (t) +
x (n-1) (t) +…+
x / (t) +
x(t) =f(t)
3. 1 - формула.
Теңдеуінің
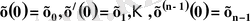
3. 2 - формула.
алғашқы шарттарды қанағаттандыратын шешуін табу керек болсын.
Мұндағы
- тұрақты сандар, ал
-алғашқы берілген мәндер.
Түпнұсқа болатын f(t) үздіксіз функция.
Белгісіз х(t) функциясы мен оның туындылары да үздіксіз болсын деп ұйғарайық. Берілген (62) теңдеудің шешуін табу үшін теңдіктің екі жағын да
-ға көбейтіп 0 мен
арасында t бойынша интегралдаймыз.
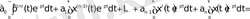
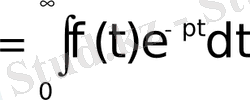
3. 3 - формула.
Осыны туындының бейнесі туралы теореманы қолданып былай жазуға болады.
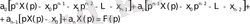
3. 4 - формула.
Мұндағы X(р) =х(t), F(р) =f(t)
Бұл теңдеу операторлық теңдеу деп аталады Оны түрлендіріп мына түрде жазайық.
(
 р
n
+
р
n
+
 р
n-1
+…+
р
n-1
+…+
 р+
р+
 ) X(р) =х
0
(
) X(р) =х
0
(
 р
n-1
+
р
n-1
+
 p
n-2
+…+
p
n-2
+…+
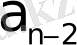 p+
p+
 ) +
) +
+х
1
(
 p
n-2
+. . +
p
n-2
+. . +
 +3p+
+3p+
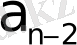 ) +a
0
х
n-1
+F(р)
) +a
0
х
n-1
+F(р)
3. 5 - формула.
Осыдан
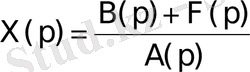
3. 6 - формула.
Мұндағы:
А(р) =
 р
n
+
р
n
+
 р
n-1
+…+
р
n-1
+…+
 p+a
n
,
p+a
n
,
В(р) =х
0
(
 р
n-1
+
р
n-1
+
 p
n-2
+…+
p
n-2
+…+
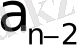 p+
p+
 ) +
) +
+x
1
(
 р
n-2
+
р
n-2
+
 p
n-3
+…+
p
n-3
+…+
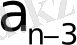 p+
p+
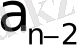 ) +
) +
+
 х
n-1
х
n-1
3. 7 - формула.
Осы () формула арқылы анықталған X(p) функциясы (62) теңдеудің шешуі болады. Егер алғашқы шарттар барлығы нөлге тең болса, онда мынадай шешу аламыз:
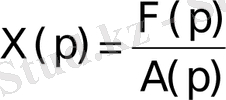
3. 8 - формула.
Дербес х(t) шешуін табу үшін X(p) бейнесіне сәйкес түпнұсқаны табу керек. Егер x 0 , х 1 , …, х n-1 алғашқы мәндері берілмеген кезкелген сандар болса, онда X(t) (62) теңдеудің дербес шешуі емес, оның жалпы шешуі болады.
3. 2 Сызықтық дифференциалдық теңдеуді Дюамель интегралын пайдаланып шешу
Берілген
 x
(n)
(t) +
x
(n)
(t) +
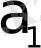 x
(n-1)
(t) +…+
x
(n-1)
(t) +…+
 x
/
(t) +
x
/
(t) +
 x(t) =f(t)
x(t) =f(t)
3. 9 - формула.
дифференциалдық теңдеуінің алғашқы x(0) =x / (0) = …=x (n-1) (0) =0
шарттарын қанағаттандыратын шешуін табу керек болсын.
Мұндағы
- тұрақты сандар, f(t) -түпнұсқа.
Теңдеудің шешуін табу үшін
 ω
(n)
(t) +
ω
(n)
(t) +
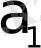 ω
(n-1)
(t) +…+
ω
(n-1)
(t) +…+
 ω
/
(t) +
ω
/
(t) +
 ω(t) =1
ω(t) =1
3. 10 - формула.
дифференциалдық теңдеуін қарастырайық.
Бұл теңдеудің ω(0) =ω / (0) =…=ω (n-1) (0) =0 алғашқы шарттарын қанағаттандыратын шешуі белгілі болсын дейік және W(p) =ω(t) сәйкестігі орындалсын.
Сонда (69) теңдеудің операторлық түрдегі теңдеуі мынадай болады:
 p
n
W(p) +
p
n
W(p) +
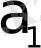 p
n-1
W(p) +…+
p
n-1
W(p) +…+
 W(p) +
W(p) +
 W(p) =
W(p) =
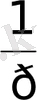
3. 11 - формула.
Осыдан
W(p) =
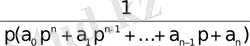
3. 12 - формула.
теңдігі алынады.
Берілген (67) теңдеудің шешуін x(t) деп, ал оның бейнесін X(p) арқылы белгімен F(p) =f(t) деп алайық.
Ал (67) теңдеу үшін операторлық теңдеуді былай жазуға болады:
 p
n
X(p) +
p
n
X(p) +
 p
n-1
X(p) +…+
p
n-1
X(p) +…+
 p
x
(p) +
p
x
(p) +
 X(p) =F(p) .
X(p) =F(p) .
3. 13 - формула.
Осыдан
X(p) =
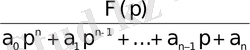
3. 14 - формула.
теңдігі анықталады. Енді (69) және (70) өрнектерді салыстырып мынадай теңдік аламыз:
X(p) =pF(p) W(p)
3. 15 - формула.
Алғашқы шарт
(0) =0 болғандықтан (54) Дюамель формуласы бойынша x(t) дербес шешуін былай жазуға болады:
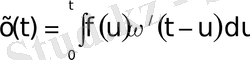
3. 16 - формула.
Немесе
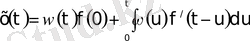
3. 17 - формула.
Функциялардың орамының қасиетін пайдаланып былай да жазуға болады:
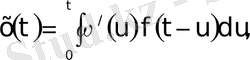
3. 18 - формула.
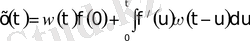
3. 19 - формула.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz