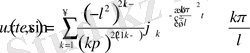Жоғары ретті туынды қатысқан бастапқы-шеттік және шеттік есептердің шешілімділігі: параболалық, гиперболалық және эллипс тектес теңдеулер


Қазақстан Республикасы Білім және Ғылым Министрлігі
Қожа Ахмет Ясауи атындағы Халықаралық Қазақ-Түрік университеті
Математика кафедрасы
Гаппаров Ибрахим Рахматуллаевич
Жоғары ретті дифференциалдық операторлар қатысқан шеттік есептердің шешілімділігін зерттеу
ДИПЛОМДЫҚ ЖҰМЫС
5В060100 - Математика
Түркістан 2020
Мазмұны
Кіріспе . . . 3
1 Параболалық тектес теңдеулер үшін жоғарғы ретті туынды қатысқан есептер
1. 1 Параболалық теңдеу үшін бастапқы шеттік есептер
1. 2. Параболалық теңдеу үшін жоғары жұп ретті туынды қатысқан шеттік есеп
1. 3. Параболалық теңдеу үшін жоғары ретті туынды қатысқан шеттік есеп
2 Гиперболалық тектес теңдеулер үшін жоғарғы ретті туынды қатысқан есептер
2. 1 Гиперболалық теңдеу үшін бастапқы шеттік есептер
2. 2 Гиперболалық теңдеу үшін жоғары ретті туынды қатысқан шеттік есеп.
3 Эллипс тектес теңдеулер үшін жоғарғы ретті туынды қатысқан есептер
3. 1 Лаплас теңдеуі үшін екінші ретті туынды қатысқан ішкі шеттік есеп
3. 2 Лаплас теңдеуі үшін екінші ретті туынды қатысқан сыртқы шеттік есеп
Қорытынды . . .
Пайдаланылған әдебиеттер . . .
КІРІСПЕ
Зерттеу тақырыбынының өзектілігі. Дипломдық жұмыс екінші ретті параболалық, гиперболалық және эллипс тектес теңдеулер үшін жоғары ретті туынды қатысқан бастапқы - шеттік және шеттік есептердің шешілімділігі мәселелерін зерттеуге арналған. Бұл есептер осы аталған теңдеулерге қарастырылатын негізгі есептердің жалпыламасы болып табылады.
Бұл тақырыптағы алғашқы жұмыс А. Н. Тихоновтың [1] мақаласында қарастырылған. Бұл мақалада шексіз аймақта параболалық тектес теңдеуі үшін жоғарғы ретті туынды қатысқан есептің айқын шешімі құрылған және мұндай есептердің термиялық тұрақтыларды анықтауға арналған құрылғыны жасаудағы қолданыстары баяндалған. Гиперболалық және эллипс тектес теңдеулер үшін осы тақырыпта зерттелінген көптеген жұмыстар бар [2-6] . Бұл жұмыстардың талдауы В. В. Карачиктің [7] монографиясында келтірілген.
Диплом жұмысының құрылымы. Жұмыс кіріспе, негізгі бөлім, қорытынды және пайдаланылған әдебиеттер тізімінен тұрады. Тұжырымдар мен формулалар нөмірлері үш көрсеткіштен құралған. Бірінші көрсеткіш - бөлім нөмерін, екінші көрсеткіш-бөлімнің ішкі бөлімінің нөмерін, үшінші көрсеткіш - сол ішкі бөлімдегі тұжырымдар мен формулалардың меншікті нөмерін көрсетеді.
Кіріспеде жұмыстың негізгі нәтижелері - лемма және теоремалары келтірілген.
Жұмыстың көлемі 60 бет. Әдебиеттер саны -11.
Жұмыстың негізгі мазмұны.
Бірінші бөлімнің 1. 2 - параграфында
 аймағында келесі есептер қарастырылады
аймағында келесі есептер қарастырылады
П1-Есеп.
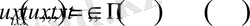

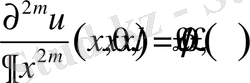
шарттарын қанағаттандыратын
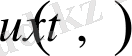 функциясын табу қажет. мұнда
функциясын табу қажет. мұнда
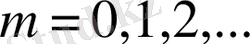
П2-Есеп.
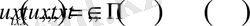

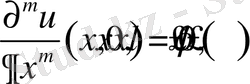
шарттарын қанағаттандыратын
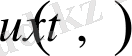 функциясын табу қажет. мұнда
функциясын табу қажет. мұнда
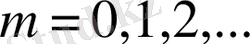
П1-есептің шешімі деп П облысында
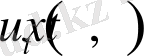 ,
,
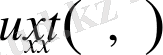 туындылары үздіксіз, П тұйық облысында
туындылары үздіксіз, П тұйық облысында
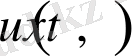 функциясының өзі және
функциясының өзі және
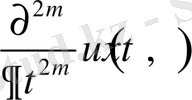 , яғни
, яғни
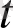 - аргумент бойынша
- аргумент бойынша
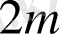 - ретті туындысы үздіксіз болатын, есептің шарттарын классикалық мағнада қанағаттандыратын
- ретті туындысы үздіксіз болатын, есептің шарттарын классикалық мағнада қанағаттандыратын
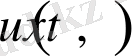 функциясына айтамыз.
функциясына айтамыз.
П1 және П2 есептерге қатысты келесі нәтижелер орынды.
Теорема 0. 1. Егер П1 және П2- есептердің шешімі бар болса ол жалғыз болады.
Теорема 0. 2. Егер
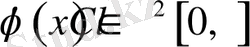 және
және
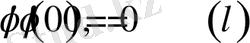 шарттары орындалса, онда П1-есептің шешімі бар және
шарттары орындалса, онда П1-есептің шешімі бар және

қатар түрінде өрнектеледі.
Бұл жерде
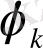 тұрақтылар
тұрақтылар
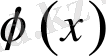 функциясының Фурье коэффиценттері, яғни
функциясының Фурье коэффиценттері, яғни
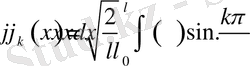
Теорема 0. 3. Егер
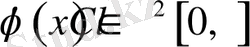 және
және
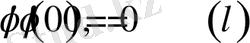 шарттары орындалса, онда П2-есептің шешімі бар және
шарттары орындалса, онда П2-есептің шешімі бар және
формуламен беріледі және мұндағы
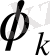 тұрақтылар
тұрақтылар
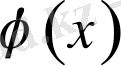 функциясының Фурье коэффициентері
функциясының Фурье коэффициентері
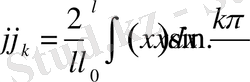
2-бөлімде гиперболалық теңдеу үшін келесі есептер қарастырылады.
 аймақта гиперболалық типтегі есептерді қарастырайық.
аймақта гиперболалық типтегі есептерді қарастырайық.
Г1-Есеп
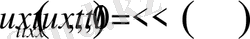
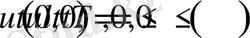
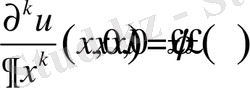
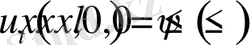
шарттарды қанағаттандыратын
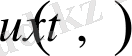 функциясын анықтау керек. Бұл жердегі k=1, 2, …
функциясын анықтау керек. Бұл жердегі k=1, 2, …
Г2-Есеп
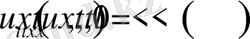 ,
,
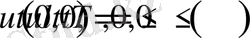 ,
,
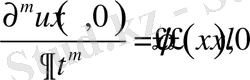 ,
,
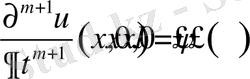 ,
,
шарттарды қанағаттандыратын
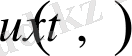 функциясын анықтау керек. Бұл жердегі k=1, 2, …
функциясын анықтау керек. Бұл жердегі k=1, 2, …
Г1-есеп үшін келесі теорема орынды.
Теорема 0. 4.
Егер
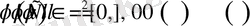 ,
,
 ,
,
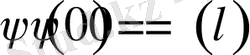 шарттары орындалса, онда Г1-есептің шешімі бар және
шарттары орындалса, онда Г1-есептің шешімі бар және
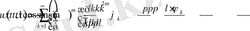 (2. 3. 5)
(2. 3. 5)
қатар түрінде өрнектеледі.
Бұл жерде
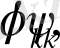 тұрақтылар
тұрақтылар
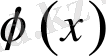 және
және
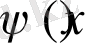 функцияларының Фурье коэффиценттері, яғни
функцияларының Фурье коэффиценттері, яғни
 .
.
Г2-есеп үшін негізгі нәтиже келесі теоремада баяндалады.
Теорема 0. 5.
Егер
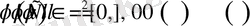 ,
,
 ,
,
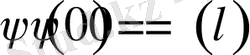 шарттары орындалса, онда Г2-есептің шешімі бар және
шарттары орындалса, онда Г2-есептің шешімі бар және
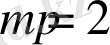 - жұп болса
- жұп болса
 .
.
түрде, ал
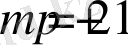 - тақ болса
- тақ болса

қатар түрінде өрнектеледі.
Бұл жерде
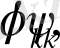 тұрақтылар
тұрақтылар
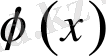 және
және
 функцияларының Фурье коэффиценттері, яғни
функцияларының Фурье коэффиценттері, яғни
 .
.
3-бөлімнің 1. 3 - параграфында Лаплас теңдеуі үшін дөнгелекте, екінші ретті туынды қатысқан ішкі және сыртқы шеттік есептер зертелінеді. қарастырылатын есептердің шешімі бар болу шарттары анықталып, есептің шешімі жалпыланған Пуассон интгералы арқылы өрнектелетіні туралы теоремалар дәлелденеді.
Бірлік дөңгелектің ішінде
∆ U(ρ, ϕ ) =0 (0. 1)
теңдеуді және оның шекарасында
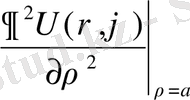 =f(ϕ )
(0. 2)
=f(ϕ )
(0. 2)
шекаралық шартты қанағаттандыратын u(ρ, ϕ ) функциясын табу керек.
Теорема 0. 6. f(ϕ) үзіліссіз функциясы болсын. (0. 1) -(0. 2) есептің шешімі бар болуы үшін
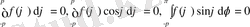
шарттарының орындалуы қажетті және жеткілікті.
Егер есептің шешімі бар болса, ол
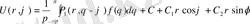
интегралы түрінде өрнектеледі.
Бұл жерде
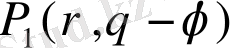 функциясы
функциясы
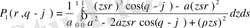
интегралымен анықталады.
Осындай нәтижені сыртқы шеттік есеп үшінде қарастыруға болады.
Мұнда (0. 1) - теңдеу дөнгелектің сыртында орындалуы қажет және (0. 2) шартқа қосымша
U(ρ, ϕ ) ≤ M, ρ→∞, M-тұрақты (0. 3)
шарттыда талап етеміз
Бұл есеп үшін келесі нәтиже орынды
Теорема 3. 2. 1. f(ϕ) үзіліссіз функция болсын. (0. 1) -(0. 3) есептің шешімі бар болуы үшін
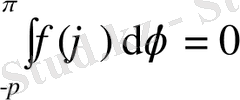
шартының орындалуы қажетті және жеткілікті.
Егер есептің шешімі бар болса, ол
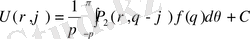
интегралымен өрнектеледі.
Бұл жерде
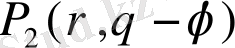 функциясы
функциясы
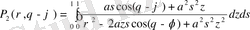
интегралымен анықталады.
1 ПАРАБОЛАЛЫҚ ТЕКТЕС ТЕҢДЕУЛЕР ҮШІН ЖОҒАРҒЫ РЕТТІ ТУЫНДЫ ҚАТЫСҚАН ЕСЕПТЕР
1. 1 Параболалық теңдеу үшін бастапқы шеттік есептер
Алдымен параболалық типтегі теңдеуі үшін классикалық бастапқы - шеттік есепке қатысты мәліметтерді келтіреміз.
 аймақта параболалық типтегі теңдеуі үшін келесі есепті қарастырайық
аймақта параболалық типтегі теңдеуі үшін келесі есепті қарастырайық
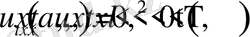 (1. 1. 1)
(1. 1. 1)
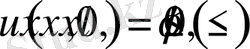 (1. 1. 2)
(1. 1. 2)
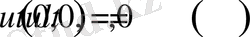 (1. 1. 3)
(1. 1. 3)
(1. 1. 1) - (1. 1. 3) есептің шешімі деп П облысында
 функциялары үздіксіз,
функциялары үздіксіз,
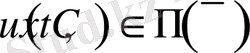 болатын және (1. 1. 1) - (1. 1. 3) шарттарды классикалық мағнада қанағаттандаратын
болатын және (1. 1. 1) - (1. 1. 3) шарттарды классикалық мағнада қанағаттандаратын
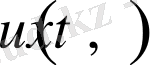 функциясына айтамыз.
функциясына айтамыз.
Бұл есептің шешімін
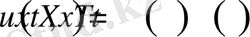 (1. 1. 4)
(1. 1. 4)
түрінде іздейік. (1. 1. 4) - теңдікпен анықталған функция үшін
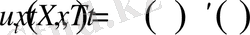
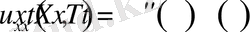
болатыны айқын. Егер(1. 1. 4) функцияны (1. 1. 1) -теңдікке қойсақ, онда
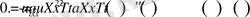
Демек,

Соңғы теңдікте
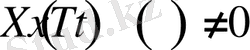 деп есептеп, теңдіктің оң және сол жақтарын
деп есептеп, теңдіктің оң және сол жақтарын
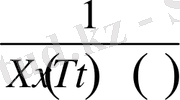 функциясына көбейтсек нәтижеде
функциясына көбейтсек нәтижеде
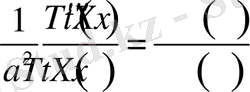 (1. 1. 5)
(1. 1. 5)
теңдікке ие боламыз.
(1. 1. 5) -теңдіктің сол жағында t аргументке, ал оң жағында x аргументке тәуелді функциялар қатысады. Бұл теңдік орынды болуы үшін олар қандайда бір тұрақтыға тең болуы қажет, яғни
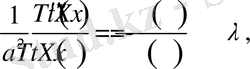
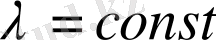 (тұрақты) .
(тұрақты) .
Сонымен,
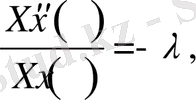
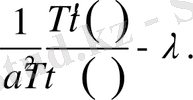
Бұл теңдеулерді
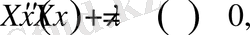
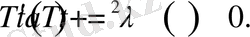
түрінде жазып аламыз. Егер (1. 1. 1) - (1. 1. 3) есептегі (1. 1. 3) - шеттік шартты есепке алсақ, онда
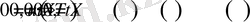
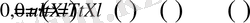
Сонымен, белгісіз
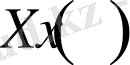 функциясы үшін келесі
функциясы үшін келесі
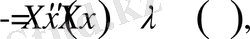
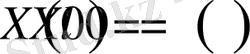 (1. 1. 6)
(1. 1. 6)
спектралдық есепті аламыз.
Бұл есептің
 түріндегі шешімдері ([8], 198-бет)
түріндегі шешімдері ([8], 198-бет)
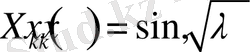
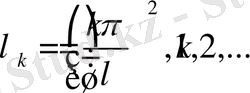
функциялар болады.
Ал
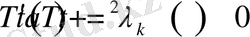
теңдеудің шешімі
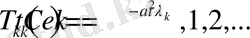
теңдікпен анықталады. Мұндағы
 - кез-келген тұрақтылар.
- кез-келген тұрақтылар.
Әрбір
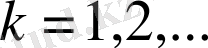 мәндерінде
мәндерінде
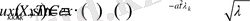
функциялары (1. 1. 1) теңдеуді және(1. 1. 3) шеттік шарттарды қанағаттандырады.
Олай болса, (1. 1. 1) - (1. 1. 3) есептің шешімін
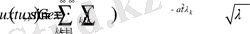 (1. 1. 7)
(1. 1. 7)
түрінде іздестіреміз.
Есептің шарты бойынша (1. 1. 7) формуламен анықталған
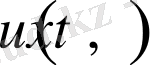 функция (1. 1. 2) - шартыда қанағаттандыруы қажет, яғни
функция (1. 1. 2) - шартыда қанағаттандыруы қажет, яғни

Демек,
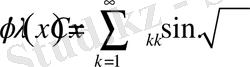 (1. 1. 8)
(1. 1. 8)
(1. 1. 8) - теңдіктің екі жағын
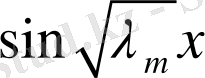 функциясына көбейтіп
функциясына көбейтіп
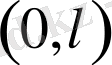 аралығында интегралдайық:
аралығында интегралдайық:
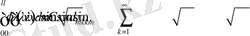
Егер
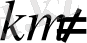 болса, онда
болса, онда
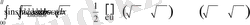
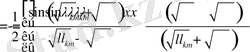
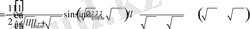
Бұл жерде біз
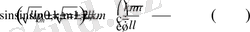
теңдігінен пайдаландық.
Егер
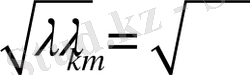 болса, онда
болса, онда
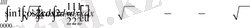
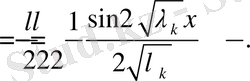
Сонымен,

Демек, белгісіз
 коэффициентер
коэффициентер
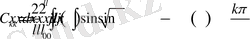 (1. 1. 9)
(1. 1. 9)
теңдікпен анықталады екен. Мұндағы
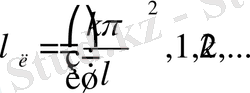
Бізге кейінгі зерттеулерде(1. 1. 9) формуладағы
 формуладағы
формуладағы
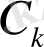 коэффициентер үшін кейбір бағалаулар керек болады. Осы бағалауларды орындайық. (1. 1. 9) интегралды бөліктеп интегралдау арқылы төмендегі нәтижеге ие боламыз:
коэффициентер үшін кейбір бағалаулар керек болады. Осы бағалауларды орындайық. (1. 1. 9) интегралды бөліктеп интегралдау арқылы төмендегі нәтижеге ие боламыз:
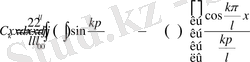
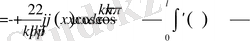
Егер
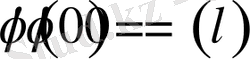 шарттары орындалса, онда
шарттары орындалса, онда
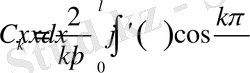
Соңғы интегралды тағы бір рет бөліктеп интегралдасақ, онда
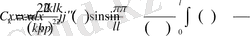
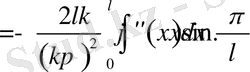
Соңғы теңсіздіктен келесі нәтиже келіп шығады
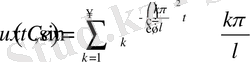
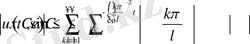
Егер
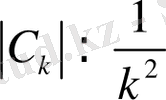 онда
онда
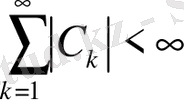
Лемма 1. Егер
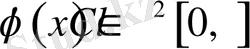 және
және
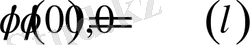 шарттарын қанағаттандырса, онда
шарттарын қанағаттандырса, онда
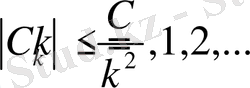 (1. 1. 10)
(1. 1. 10)
теңсіздігі орынды, мұнда С - тұрақты.
Теорема 1. Егер
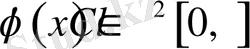 және
және
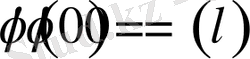 болса, онда (1. 1. 1) - (1. 1. 3) есептің шешімі бар және ол
болса, онда (1. 1. 1) - (1. 1. 3) есептің шешімі бар және ол
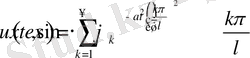
теңдігімен анықталады. Бұл жерде
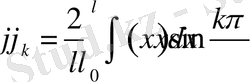
1. 2. Параболалық теңдеу үшін жоғары жұп ретті туынды қатысқан шеттік есеп
 аймағында келесі есептерді қарастырамыз.
аймағында келесі есептерді қарастырамыз.
1-Есеп.
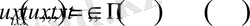 (1. 2. 1)
(1. 2. 1)
 (1. 2. 2)
(1. 2. 2)
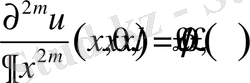 (1. 2. 3)
(1. 2. 3)
шарттарын қанағаттандыратын
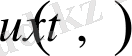 функциясын табу қажет. мұнда
функциясын табу қажет. мұнда
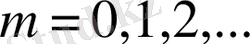
1-Есептің шешімін
(1. 2. 4)
қатар түрінде іздестірейік.
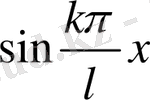 функциясы
функциясы
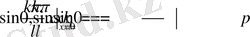 шарттарды қанағаттандырады. Сол себептен (1. 2. 4) қатар мен анықталған функция үшін (1. 2. 2) шарттар орындалады.
шарттарды қанағаттандырады. Сол себептен (1. 2. 4) қатар мен анықталған функция үшін (1. 2. 2) шарттар орындалады.
Егер (1. 2. 4) функцияны (1. 2. 1) теңгеуге қойсақ онда
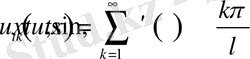
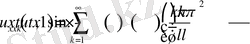
Бұдан
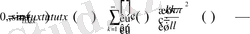
Демек, кез-келген
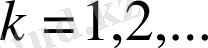 үшін
үшін
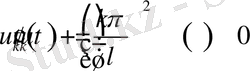 (1. 2. 5)
(1. 2. 5)
теңдігі орындалуы қажет.
(1. 2. 5) теңдеудің шешімі
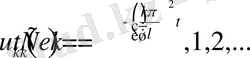
формуламен анықталады, мұндағы
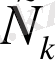 - тұрақтылар. Олай болса, (1. 2. 1)
- тұрақтылар. Олай болса, (1. 2. 1)
теңдеудің шешімі
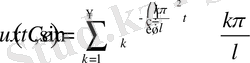
формуламен анықталады. Бұл функция (1. 2. 3) шарттыда қанағаттандыру керек. Егер
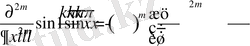
теңдігін есепке алсақ, онда
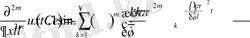
Бұдан
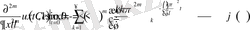 (1. 2. 6)
(1. 2. 6)
Айталық,
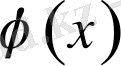 функциясы
функциясы
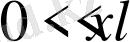 аралығында
аралығында
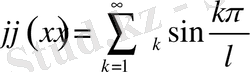
түріндегі Фурье қатарына жіктелсін, мұнда
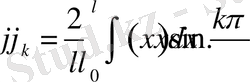 (1. 2. 7)
(1. 2. 7)
Онда, (1. 2. 6) және(1. 2. 7) қатарларды теңестіріп
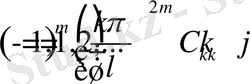
теңдігін аламыз.
Бұдан белгісіз
коэффицентер
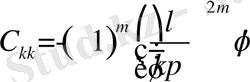
теңдіктен анықталады.
Олай болса, (1. 2. 1) - (1. 2. 3) есебінің шешімі
(1. 2. 8)
формуламен беріледі және мұндағы
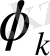
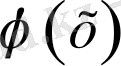 функциясының Фурье коэффициентері
функциясының Фурье коэффициентері
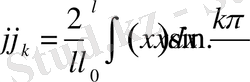
Біз 1-есептің шешімін тапқан кезде бұл шешім, яғни
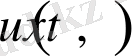 функциясы алдымен П облысында(1. 2. 1) - теңдеуді қанағаттандыруы керек. Теңдеудің берілуі бойынша табылған функцияның
функциясы алдымен П облысында(1. 2. 1) - теңдеуді қанағаттандыруы керек. Теңдеудің берілуі бойынша табылған функцияның
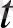 - аргументі бойынша туындысы бар және П облысында үздіксіз. Осы шарт
- аргументі бойынша туындысы бар және П облысында үздіксіз. Осы шарт
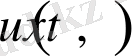 функциясының
функциясының
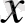 - аргументі бойынша екінші ретті туындысына да талап етіледі, яғни
- аргументі бойынша екінші ретті туындысына да талап етіледі, яғни
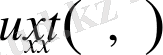 П облысында үздіксіз болуы қажет.
П облысында үздіксіз болуы қажет.
Егер(1. 2. 2) назар салсақ онда
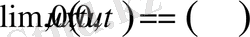
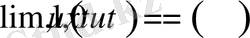
шарттары орындалуы қажет. Олай болса,
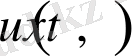 функциясы
функциясы
 тұйық облыста үздіксіз болуы қажет. Соңғы (1. 2. 3) - шарт
тұйық облыста үздіксіз болуы қажет. Соңғы (1. 2. 3) - шарт

түрінде анықталады. Осы шарттан
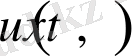 функциясының
функциясының
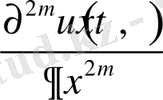 , яғни
, яғни
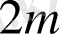 - ретті туындысы П тұйық облыста үздіксіз болуын қажет етеді. Сонымен келесі анықтаманы береміз.
- ретті туындысы П тұйық облыста үздіксіз болуын қажет етеді. Сонымен келесі анықтаманы береміз.
Анықтама1. 1-Есептің шешімі деп П облысында
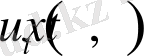 ,
,
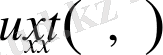 туындылары үздіксіз, П тұйық облысында
туындылары үздіксіз, П тұйық облысында
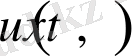 функциясының өзі және
функциясының өзі және
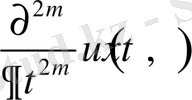 , яғни
, яғни
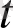 - аргумент бойынша
- аргумент бойынша
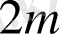 - ретті туындысы үздіксіз болатын, (1. 2. 1) - (1. 2. 3) шарттарды қанағаттандыратын
- ретті туындысы үздіксіз болатын, (1. 2. 1) - (1. 2. 3) шарттарды қанағаттандыратын
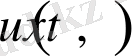 функциясына айтамыз.
функциясына айтамыз.
Енді (1. 2. 8) формуламен анықталған
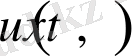 функциясы 1-есептің шын мәнісінде шешімі, яғни 1-анықтама шарттарын қанағаттандыратынын көрсетейік.
функциясы 1-есептің шын мәнісінде шешімі, яғни 1-анықтама шарттарын қанағаттандыратынын көрсетейік.
Алдымен,
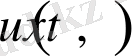 функциясының
функциясының
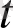 - аргумент бойынша
- аргумент бойынша
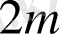 - ретті туындысы бар және ол П тұйық облыста үздіксіз болатынын көрсетеміз. Оның үшін (1. 2. 8) - теңдікпен анықталған функциядан
- ретті туындысы бар және ол П тұйық облыста үздіксіз болатынын көрсетеміз. Оның үшін (1. 2. 8) - теңдікпен анықталған функциядан
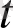 - аргумент бойынша
- аргумент бойынша
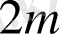 - ретті туындысын табамыз:
- ретті туындысын табамыз:
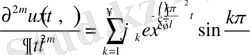 (1. 2. 9)
(1. 2. 9)
Бұдан
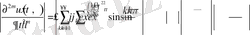
Егер
 болса, онда
болса, онда
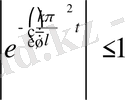
Сол сиақты
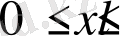 үшін
үшін
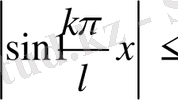 осы теңсіздіктерден
осы теңсіздіктерден
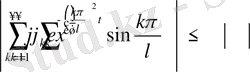
нәтижені аламыз.
Демек, біз
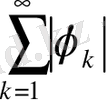 қатарды жинақтылыққа зерттеуіміз қажет.
қатарды жинақтылыққа зерттеуіміз қажет.
Анықтама бойынша
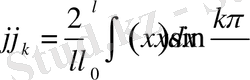
Егер
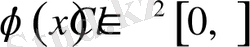 және
және
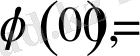
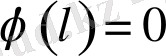 шарттары орындалса, онда 1-лемманың нәтижесі бойынша
шарттары орындалса, онда 1-лемманың нәтижесі бойынша
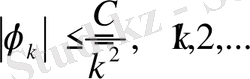
Олай болса
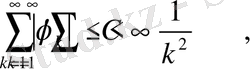
яғни
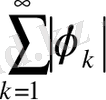 - қатар жинақталады.
- қатар жинақталады.
Демек, бұл қатар (1. 2. 9) - теңдіктің оң жағындағы қатар үшін можарант қатар болады. Онда Вейерштрасс теоремасы бойынша [11] бұл қатар П тұйық облыста бірқалыпты жинақталады және оның қосындысы осы облыста үздіксіз функция болады. Сонымен,
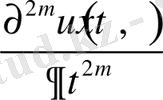 функциясы П облысында үздіксіз.
функциясы П облысында үздіксіз.
Осы сиақты
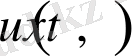 функциясына қатысты
функциясына қатысты
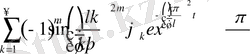
қатарды бағалайтын болсақ, онда
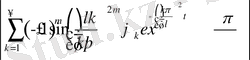
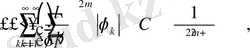
Демек, бұл қатарда П тұйық облыста бірқалыпты жинақталады, сол себептен оның қосындысы болатын
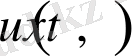 функциясы осы облыста үздіксіз функция болады. Осы сиақты
функциясы осы облыста үздіксіз функция болады. Осы сиақты
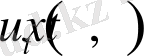 және
және
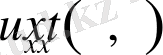 функцияларыныңда үздіксіз болатынын көрсетуге болады. Мысал үшін
функцияларыныңда үздіксіз болатынын көрсетуге болады. Мысал үшін
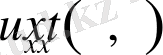 үшін келесілер орынды:
үшін келесілер орынды:
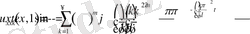
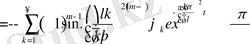
Бұдан
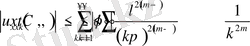
яғни
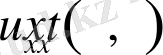 функциясы П облысында үздіксіз.
функциясы П облысында үздіксіз.
Сонымен келесі теореманы дәлелдедік.
Теорема1. Егер
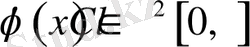 және
және
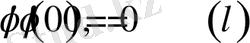 шарттары орындалса, онда 1-Есептің шешімі бар және
шарттары орындалса, онда 1-Есептің шешімі бар және

қатар түрінде өрнектеледі.
Бұл жерде
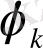 тұрақтылар
тұрақтылар
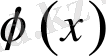 функциясының Фурье коэффиценттері, яғни
функциясының Фурье коэффиценттері, яғни
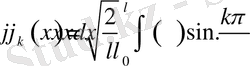
Келесі теоремада 1-есептің шешімі жалғыз болатыны дәлелденеді.
Теорема2. Егер 1-Есептің шешімі бар болса ол жалғыз болады.
Дәлелдеуі. Айталық, 1-есептің шешімі екеу, яғни
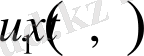 және
және
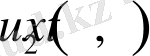 болсын.
болсын.
 деп белгілейік. Онда
деп белгілейік. Онда
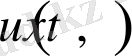 функциясы біртекті (1. 2. 1) - (1. 2. 3) шарттарды қанағаттандырады. Есептің шарты бойынша
функциясы біртекті (1. 2. 1) - (1. 2. 3) шарттарды қанағаттандырады. Есептің шарты бойынша
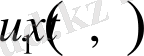 және
және
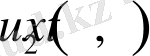 функциялары П тұйық облыста үздіксіз. Онда
функциялары П тұйық облыста үздіксіз. Онда
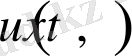 функциясыда П тұйық облысында үздіксіз функция болады. Бұл жағдайда
функциясыда П тұйық облысында үздіксіз функция болады. Бұл жағдайда
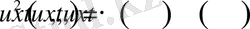 функциясыда үздіксіз және ол
функциясыда үздіксіз және ол
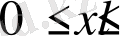 облысында интегралданатын функция.
облысында интегралданатын функция.
Егер
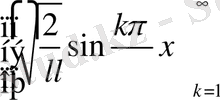 жүйесін қарастыратын болсақ бұл жүйе
жүйесін қарастыратын болсақ бұл жүйе
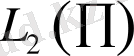 кеңістігінде ортонормал базис құрайды (мысал үшін қараңыз
кеңістігінде ортонормал базис құрайды (мысал үшін қараңыз
 ) .
) .
Сондықтан
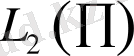 кеңістігіне тиісті болған кез келген
кеңістігіне тиісті болған кез келген
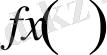 функциясы осы жүйе бойынша Фурье қатарына жіктеледі. Біздің жағдайда
функциясы осы жүйе бойынша Фурье қатарына жіктеледі. Біздің жағдайда
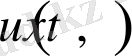 функциясы
функциясы
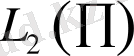 кеңістігіне тиісті. Сол себептен
кеңістігіне тиісті. Сол себептен
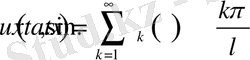
Бұл жерде
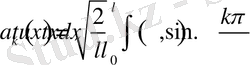
Осы теңдіктен t - умент бойынша дифференциалдасақ, онда

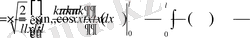
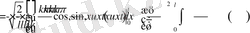

Демек,
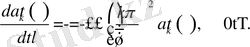
Бұл теңдеудің шешімі
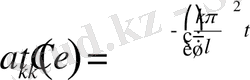
Егер
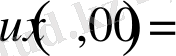 болатынын ескерсек, онда
болатынын ескерсек, онда
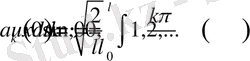
онда

Сонда
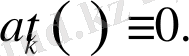 Бұдан
Бұдан
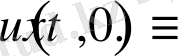
Теорема дәлелденді.
1. 3. Параболалық теңдеу үшін жоғары ретті туынды қатысқан шеттік есеп
2-Есеп.
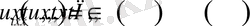 (1. 3. 1)
(1. 3. 1)
 (1. 3. 2)
(1. 3. 2)
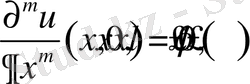 (1. 3. 3)
(1. 3. 3)
шарттарын қанағаттандыратын
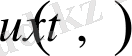 функциясын табу қажет. мұнда
функциясын табу қажет. мұнда
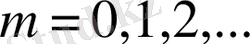
2-Есептің шешімін
(1. 3. 4)
қатар түрінде іздестірейік.
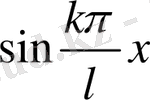 функциясы
функциясы
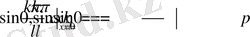 шарттарды қанағаттандырады. Сол себептен (1. 3. 4) қатар мен анықталған функция үшін (1. 3. 2) шарттар орындалады.
шарттарды қанағаттандырады. Сол себептен (1. 3. 4) қатар мен анықталған функция үшін (1. 3. 2) шарттар орындалады.
Егер (1. 3. 4) функцияны(1. 3. 1) теңгеуге қойсақ онда
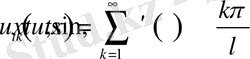
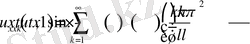
Бұдан
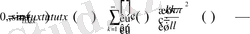
Демек, кез-келген
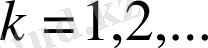 үшін
үшін
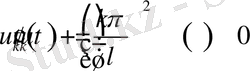 (1. 3. 5)
(1. 3. 5)
теңдігі орындалуы қажет.
(1. 3. 5) теңдеудің шешімі
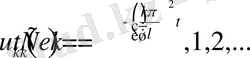
формуламен анықталады, мұндағы
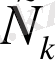 - тұрақтылар. Олай болса, (1. 3. 1) теңдеудің шешімі
- тұрақтылар. Олай болса, (1. 3. 1) теңдеудің шешімі
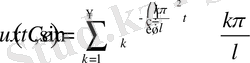
формуламен анықталады. Бұл функция (1. 3. 3) шарттыда қанағаттандыру керек. Бұл функцияның ол шартты қанағаттандыруының 2 түрлі жағдайы болады. Егер
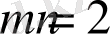 және
және
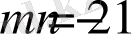 болған жағдайлар. Осы ә жағдайды жеке жеке қарастырып шығайық.
болған жағдайлар. Осы ә жағдайды жеке жеке қарастырып шығайық.
- Егерболса
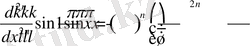
теңдігін есепке алсақ, онда
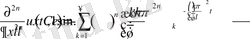
Бұдан
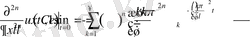
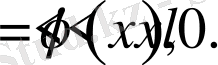 (1. 3. 6)
(1. 3. 6)
Айталық,
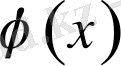 функциясы
функциясы
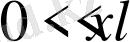 аралығында
аралығында
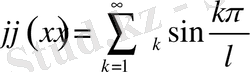
түріндегі Фурье қатарына жіктелсін, мұнда
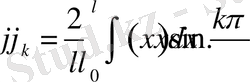 (1. 3. 7)
(1. 3. 7)
Онда, (1. 3. 6) және (1. 3. 7) қатарларды теңестіріп
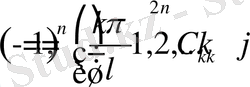
теңдігін аламыз.
Бұдан белгісіз
коэффицентер
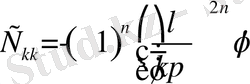
теңдіктен анықталады.
Олай болса,
-
есебінің шешімі
(1. 3. 8)
формуламен беріледі және мұндағы
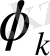
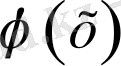 функциясының Фурье коэффициентері
функциясының Фурье коэффициентері
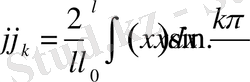
- Егерболса
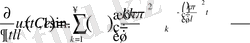
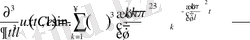
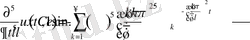
Ал енді жалпы түрін жазайық
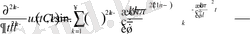 (1. 3. 9)
(1. 3. 9)
Бұдан
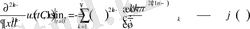
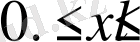 (1. 3. 10)
(1. 3. 10)
Айталық,
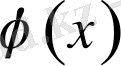 функциясы
функциясы
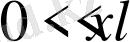 аралығында
аралығында
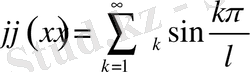
түріндегі Фурье қатарына жіктелсін, мұнда
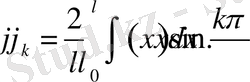 (1. 3. 11)
(1. 3. 11)
Онда, (1. 3. 10) және(1. 3. 11) қатарларды теңестіріп

теңдігін аламыз.
Бұдан белгісіз
коэффицентер
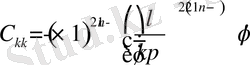
теңдіктен анықталады.
Олай болса, (1. 3. 1) - (1. 3. 3) есебінің шешімі
(1. 3. 12)
формуламен беріледі және мұндағы
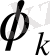 коэффициенттері
коэффициенттері
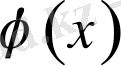 функциясының Фурье коэффициентері
функциясының Фурье коэффициентері
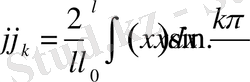
2 ГИПЕРБОЛАЛЫҚ ТЕКТЕС ТЕҢДЕУЛЕР ҮШІН ЖОҒАРҒЫ РЕТТІ ТУЫНДЫ ҚАТЫСҚАН ЕСЕПТЕР
2. 1 Гиперболалық теңдеу үшін бастапқы шеттік есептер
Алдымен гиперболалық типтегі теңдеуі үшін классикалық бастапқы - шеттік есепке қатысты мәліметтерді келтіреміз.
 аймақта гиперболалық типтегі теңдеуі үшін келесі есепті қарастырайық
аймақта гиперболалық типтегі теңдеуі үшін келесі есепті қарастырайық
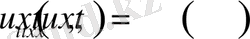 (2. 1. 1)
(2. 1. 1)
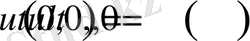 (2. 1. 2)
(2. 1. 2)
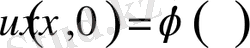 (2. 1. 3)
(2. 1. 3)
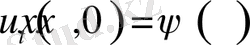 (2. 1. 4)
(2. 1. 4)
Бұл гиперболалық есептің шешімін
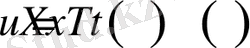 түрінде іздесек, онда (2. 1. 1) теңдік бойынша u дан t бойынша 2 рет және x бойынша 2 рет туынды алатын боламыз. Ал енді сол туындыларды төмендегі өрнектер арқылы қарастырамыз.
түрінде іздесек, онда (2. 1. 1) теңдік бойынша u дан t бойынша 2 рет және x бойынша 2 рет туынды алатын боламыз. Ал енді сол туындыларды төмендегі өрнектер арқылы қарастырамыз.
 бұл t бойынша 2 ретті туынды.
бұл t бойынша 2 ретті туынды.
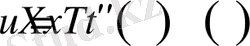 бұл x бойынша 2 ретті туынды.
бұл x бойынша 2 ретті туынды.
Төбеде алған нәтижелерді (2. 1. 1) теңдікке апарып қойсақ, онда біз
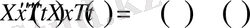 теңдігіне келеміз.
теңдігіне келеміз.
Соңғы алған теңдіктің екі жағын
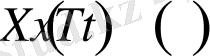 ға бөлейік, сол бөлуді орындау арқасында біз
ға бөлейік, сол бөлуді орындау арқасында біз
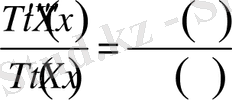 теңдікке келеміз. Ең соңғы алған теңдігіміздің сол жағы t ға қатысты, ал оң жағы x ке қатысты функция болып тұрғаны көрініп тұр. Бұл теңдіктерді -λ тең деп алып система құрайық.
теңдікке келеміз. Ең соңғы алған теңдігіміздің сол жағы t ға қатысты, ал оң жағы x ке қатысты функция болып тұрғаны көрініп тұр. Бұл теңдіктерді -λ тең деп алып система құрайық.
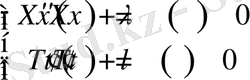
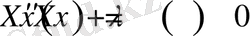
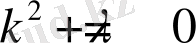
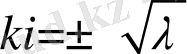
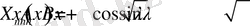 (2. 1. 5)
(2. 1. 5)
Енді шыққан (2. 1. 5) функцияға шеттік шарттарды қойып тексеріп көреміз.
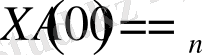
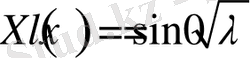
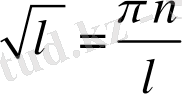
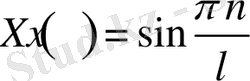 (2. 1. 6)
(2. 1. 6)
Біз шеттік шарттарды қою арқылы
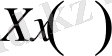 функциясын таптық, ал енді дәл сол тәсіл арқылы
функциясын таптық, ал енді дәл сол тәсіл арқылы
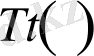 функциясын табыйық
функциясын табыйық
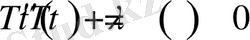
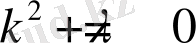
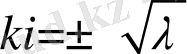
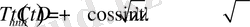 (2. 1. 7)
(2. 1. 7)
Ең соңғы алған (2. 1. 6) және (2. 1. 7) теңдеулерді біріктіріп жазайық.
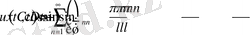 (2. 1. 8)
(2. 1. 8)
Енді (2. 1. 8) функцияны (2. 1. 3) шартпен тексеріп көрейік.

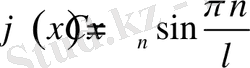 (2. 1. 9)
(2. 1. 9)
функциясын аламыз.
Енді (2. 1. 8) функциядан t бойынша 1 рет туынды алайық.

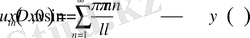
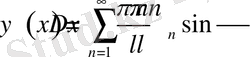 (2. 1. 10)
(2. 1. 10)
Енді (2. 1. 9) және (2. 1. 10) функцияларының екі жағын да
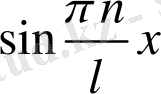 ке көбейтіп
0<x<l
аралығында интегралдасақ, онда төмендегі нәтижелерді аламыз.
ке көбейтіп
0<x<l
аралығында интегралдасақ, онда төмендегі нәтижелерді аламыз.
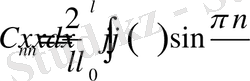
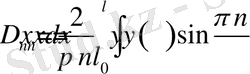 (2. 1. 11)
(2. 1. 11)
(2. 1. 8) функциясы шеттік шарттарды қанағаттандыратынын тексеріп көрейік.
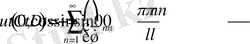
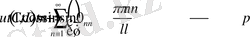
Онда біз (2. 1. 8) функцияны келесі көріністе жазып алсақ болады.
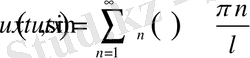 (2. 1. 12)
(2. 1. 12)
Ал енді (2. 1. 12) функцияны пайдалана отырып (2. 1. 1) теңдікті орындауға тырысып көрейік.
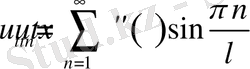
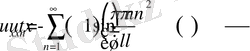
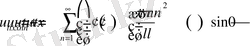
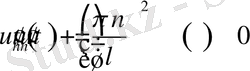
Енді
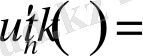 деп алайық, сол кезде
деп алайық, сол кезде
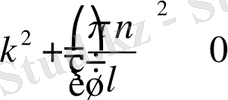
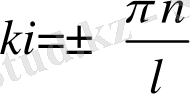
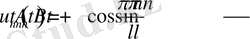 (2. 1. 13)
(2. 1. 13)
2. 2 Гиперболалық теңдеу үшін жоғары ретті туынды қатысқан шеттік есеп.
 аймақта гиперболалық типтегі есептерді қарастырайық.
аймақта гиперболалық типтегі есептерді қарастырайық.
1-Есеп
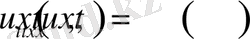 (2. 2. 1)
(2. 2. 1)
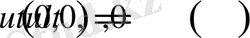 (2. 2. 2)
(2. 2. 2)
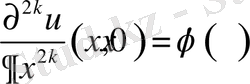 (2. 2. 3)
(2. 2. 3)
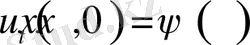 (2. 2. 4)
(2. 2. 4)
шарттарды қанағаттандыратын
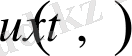 функциясын табуымыз керек. Бұл жердегі k=1, 2, …
функциясын табуымыз керек. Бұл жердегі k=1, 2, …
2-Есеп (Коши есебінің жалпыламасы)
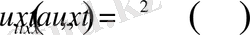 (2. 2. 5)
(2. 2. 5)
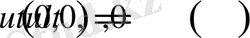 (2. 2. 6)
(2. 2. 6)
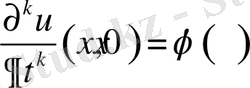 (2. 2. 7)
(2. 2. 7)
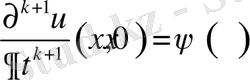 (2. 2. 8)
(2. 2. 8)
шарттарды қанағаттандыратын
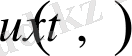 функциясын табуымыз керек. Бұл жердегі k=0, 1, 2, …
функциясын табуымыз керек. Бұл жердегі k=0, 1, 2, …
1-Есептің шешімін
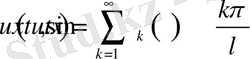
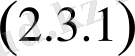
қатар түрінде іздестірейік.
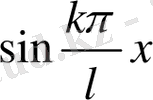 функциясы
функциясы
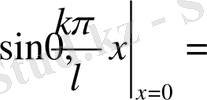
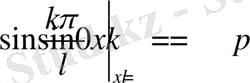
шарттарды қанағаттандырады. сол себептен
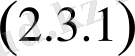 қатар мен анықталған функция үшін
қатар мен анықталған функция үшін
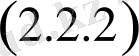 шарттар орындалады .
шарттар орындалады .
Егер
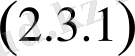 функцияны
функцияны
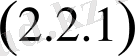 - теңдеуге қойсақ онда
- теңдеуге қойсақ онда
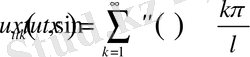
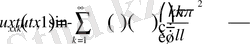
Бұдан

Демек кез - келген
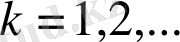 үшін
үшін
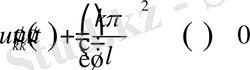
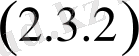
теңдігі орындалуы қажет.
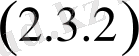 теңдеудің шешімі
теңдеудің шешімі
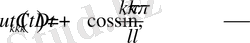
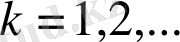
формуламен анықталады, мұндағы
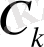 және
және
 тұрақтылар.
тұрақтылар.
Олай болса,
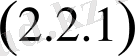 теңдеудің шешімін
теңдеудің шешімін
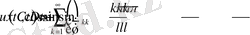
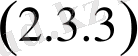
формуламен анықталады. Бұл функция
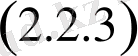 - шарттыда қанағаттандыруы қажет, яғни
- шарттыда қанағаттандыруы қажет, яғни
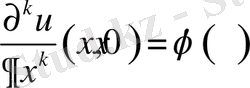
Бұл функцияның екі түрлі жағдайы болады. Егер
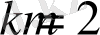 және
және
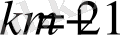 болған жағдайларды қарастырайық. Әр қайсысына жеке жеке тоқтала кетейік.
болған жағдайларды қарастырайық. Әр қайсысына жеке жеке тоқтала кетейік.
- Егерболса
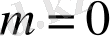 болса
болса
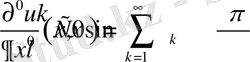
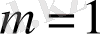 болса
болса
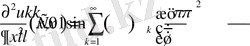
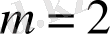 болса
болса
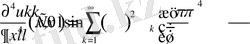
Ал енді осы алған нәтижелерден жалпы жағдайда жұп ретті туындылар үшін қарастырсақ
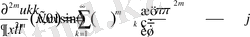
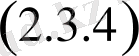
Сонда
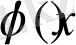 функциясы Фурье қатарына жіктелуін есепке алсақ, онда
функциясы Фурье қатарына жіктелуін есепке алсақ, онда

Бұдан
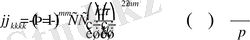
Демек, белгісіз
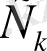 - тұрақтылар анықталды.
- тұрақтылар анықталды.
Осы сияқты (2. 2. 4) шарттан
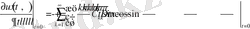
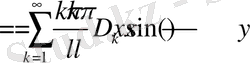
Сонымен
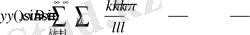 .
.
Онда
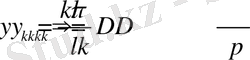 .
.
Бұдан 1-есептің формал түрдегі шешімін жазайық:
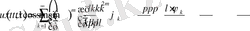
Сонымен 1-есеп үшін келесі теорема орынды.
Теорема 2. 2. 1.
Егер
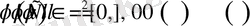 ,
,
 ,
,
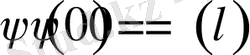 шарттары орындалса, онда 1-есептің шешімі бар және
шарттары орындалса, онда 1-есептің шешімі бар және
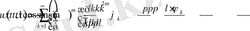 (2. 3. 5)
(2. 3. 5)
қатар түрінде өрнектеледі.
Бұл жерде
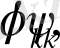 тұрақтылар
тұрақтылар
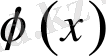 және
және
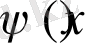 функцияларысының Фурье коэффиценттері, яғни
функцияларысының Фурье коэффиценттері, яғни
 .
.
Дәлелдеуі.
Теореманы толық дәлелдеу үшін (2. 3. 5) қатармен анықталған
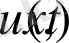 функциясының есептің шартында қатысатын туындылары бар болатынын дәлелдесек жеткілікті.
функциясының есептің шартында қатысатын туындылары бар болатынын дәлелдесек жеткілікті.
1)
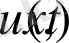 функция
функция
 облысында
облысында
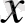 және
және
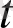 аргументтері бойынша екінші ретті туындыға ие болуы қажет. Соны көрсетейік. Оның үшін (2. 3. 5) қатарды екі рет дифференциалдап нәтижеде алынған қатардың бір қалыпты жинақтылығын дәлелдейміз:
аргументтері бойынша екінші ретті туындыға ие болуы қажет. Соны көрсетейік. Оның үшін (2. 3. 5) қатарды екі рет дифференциалдап нәтижеде алынған қатардың бір қалыпты жинақтылығын дәлелдейміз:
 (2. 3. 6)
(2. 3. 6)
Бұдан
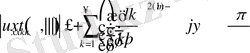
Соңғы қатарды жинақтылыққа зерттеу үшін келесі екі қатарларды қарастырамыз
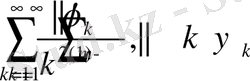
Шартымыз бойынша
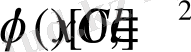 , ал Фурье коэффициентерінің анықтамасы бойынша
, ал Фурье коэффициентерінің анықтамасы бойынша
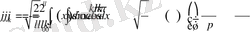
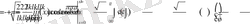
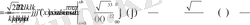 .
.
Сонымен
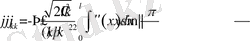 .
.
Олай болса, кез келген
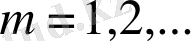 үшін
үшін
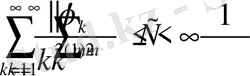 .
.
Осы сияқты шартымыз бойынша
 және осы функцияның Фурье коэффициентері үшін
және осы функцияның Фурье коэффициентері үшін
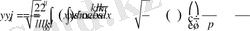
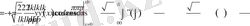
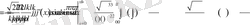 .
.
Сонымен
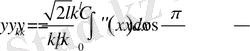 .
.
Бұл жерде
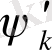 - тұрақтылар
- тұрақтылар
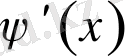 функциясының Фурье коэффициенттері. Теорема шарты бойынша
функциясының Фурье коэффициенттері. Теорема шарты бойынша
 . Онда
. Онда
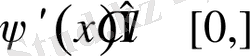 , ал кез келген үздіксіз функцияның квадраты интегралданатын функция, яғни
, ал кез келген үздіксіз функцияның квадраты интегралданатын функция, яғни
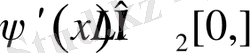 .
.
[9] әдебиетте кез келген
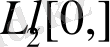 класқа тиісті функцияны Фурье коэффициенттері үшін Бессель теңсіздігі орынды болатынын дәлелденген. Осы теңсіздік бойынша
класқа тиісті функцияны Фурье коэффициенттері үшін Бессель теңсіздігі орынды болатынын дәлелденген. Осы теңсіздік бойынша
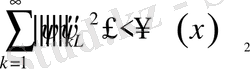
Олай болса, кез келген
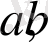 үшінорынды болатын мына
үшінорынды болатын мына
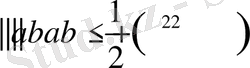 теңсзідіктен
теңсзідіктен
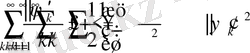 .
.
Cонымен
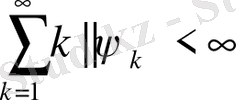
Бұдан (2. 3. 6) - қатардың бірқалыпты жинақтылығы, оның нәтижесінде осы қатардың қосындысы болған
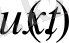 функциясы үшін
функциясы үшін
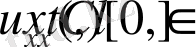 келіп шығады. Осы сияқты
келіп шығады. Осы сияқты
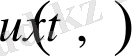 ,
,
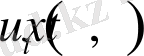 ,
,
 функцияларына сәйкес келетін қатарлардында бірқалыпты жинақтылығын дәлелдеуге болады. Теорема дәлелденді.
функцияларына сәйкес келетін қатарлардында бірқалыпты жинақтылығын дәлелдеуге болады. Теорема дәлелденді.
Ендікелесі, яғни 2-есепті зерттеуге өтейік. Бұл есептің шешімін
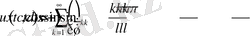 (2. 2. 6)
(2. 2. 6)
қатар түрінде іздестірейік. Мұндағы
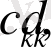 - белгісіз коэффициентер.
- белгісіз коэффициентер.
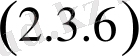 функция
функция
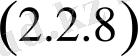 (2. 2. 9) шарттардыда қанағаттандыруы керек, яғни
(2. 2. 9) шарттардыда қанағаттандыруы керек, яғни
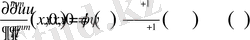 .
.
Бұл теңдікті зерттеу үшін
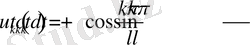 функцияның
функцияның
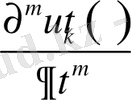 туындысын айқындау қажет. Осы мәселемен айналысамыз.
туындысын айқындау қажет. Осы мәселемен айналысамыз.
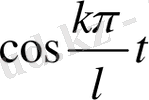 функциясы үшін
функциясы үшін
 ,
,
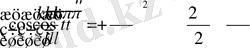 ,
,
…
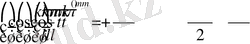 .
.
Осы сияқты
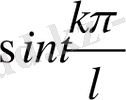 функциясы үшін
функциясы үшін
 ,
,
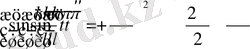 ,
,
…
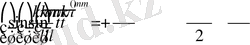 .
.
Олай болса,
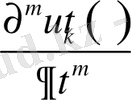 туынды үшін
туынды үшін
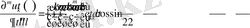 .
.
Осы есепетулердің нәтижесінде
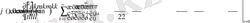
 ,
,
және
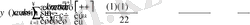
болады. Егер
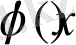 және
және
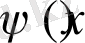 функцияларын Фурье қатары түрінде өрнектеп, жоғарыдағы қатарлармен теңестірсек, онда
функцияларын Фурье қатары түрінде өрнектеп, жоғарыдағы қатарлармен теңестірсек, онда
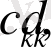 - белгісіз коэффициентер үшін келесі
- белгісіз коэффициентер үшін келесі
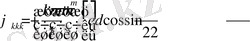 ,
,
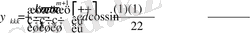
алгебралық теңдеулер жүйесін аламыз.
Бұл теңдеулер жүйесін осылайша
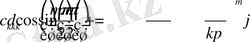 ,
,

жазып алуға болады. Соңғы жүйенің анықтауышы


Онда Крамер әдісі бойынша
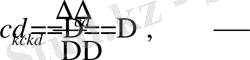 .
.
Мұндағы

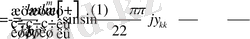
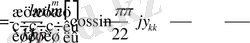 ,
,

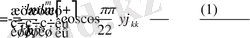
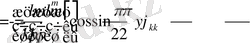
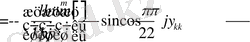 .
.
Сонымен жүйенің шешімдері
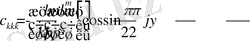
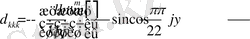 .
.
Бұл есепетеулердің нәтижесінде 2-есептің шешімінде қатысатын
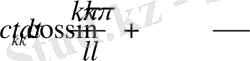 функция үшін
функция үшін
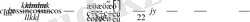





 .
.
Сонда 2-есептің шешімін
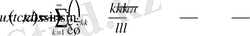

 .
.
өрнектеуге болады.
Осы жерде екі жағдай болуы мүмкін:
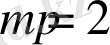 - жұп сан немесес
- жұп сан немесес
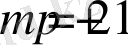 - тақ сан.
- тақ сан.
Егер
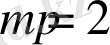 - жұп болса, онда
- жұп болса, онда
 ,
,
ал егерде
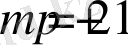 - тақ болса
- тақ болса
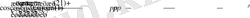
Сонымен
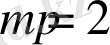 - жұп болса
- жұп болса

 ,
,
егер
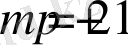 - тақ болса
- тақ болса

 .
.
Бұдан
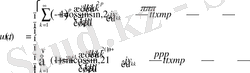 .
.
теңдіктерге келеміз.
Сонымен Г2-есепке қатысты келесі теореманы дәлелдедік.
Теорема 2. 2. 2.
Егер
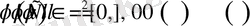 ,
,
 ,
,
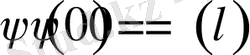 шарттары орындалса, онда 2-есептің шешімі бар және
шарттары орындалса, онда 2-есептің шешімі бар және
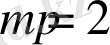 - жұп болса
- жұп болса

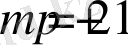 - тақ болса
- тақ болса

қатар түрінде өрнектеледі.
Бұл жерде
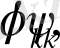 тұрақтылар
тұрақтылар
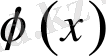 және
және
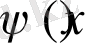 функцияларысының Фурье коэффиценттері, яғни
функцияларысының Фурье коэффиценттері, яғни
 .
.
Мысалдар.
1-Мысал.
Г2-есепте
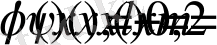 болсын. Онда
болсын. Онда
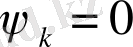 болатыны айқын. Ал
болатыны айқын. Ал
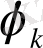 коэффициенттер
коэффициенттер

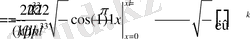 .
.
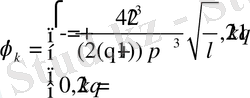 .
.
Сонымен есептің шешімі
 .
.
2-Мысал.
Г2-есепте
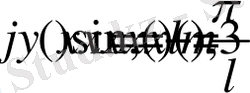 болсын. Бұл жағдайда
болсын. Бұл жағдайда
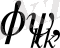 коэффициенттерүшін
коэффициенттерүшін
 .
.
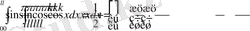
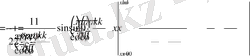 .
.
Бұдан
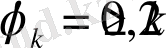 . Осылайша
. Осылайша

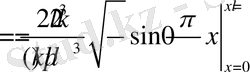 .
.
Сонымен есептің шешімі
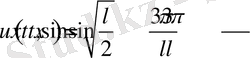 .
.
3 ЭЛЛИПС ТЕКТЕС ТЕҢДЕУЛЕР ҮШІН ЖОҒАРҒЫ РЕТТІ ТУЫНДЫ ҚАТЫСҚАН ЕСЕПТЕР
3. 1 Лаплас теңдеуі үшін екінші ретті туынды қатысқан ішкі шеттік есеп
Осы көрсетілген параграфта Лаплас теңдеуі үшін дөнгелекте, екінші ретті туынды қатысқан ішкі және де сыртқы шеттік есептер қарастырылып зертелінеді. Осы жерде қарастырылатын есептердің шешімі бар болу шарттары анықталып, есептің жауабы яғни шешімі жалпыланған Пуассон интегралы арқылы жазылып өрнектелетіні туралы теоремалар дәлелденеді.
Бірлік дөңгелекте мына келесі түрде берілген ішкі есепті қарастырайық:
Дөңгелектің ішкі бөлігінде
∆ U(ρ, ϕ ) =0 (3. 1. 1)
теңдеуін және де оның шекарасындағы
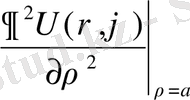 =f(ϕ )
(3. 1. 2)
=f(ϕ )
(3. 1. 2)
шекаралық шартын қанағаттандыратын u(ρ, ϕ ) функциясын табуымыз қажет.
Бұл жердегі f(ϕ ) - дөңгелектің шекарасында, яғни шеңбердегі берілген функция болып табылады.
Есептің шешімін келесі түрдегі гармониялық функциялар үшін анықталған мына түрдегі
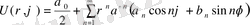
қатар түрінде іздестіреміз.
Мысалыға айталық, бұл функциямыз (3. 1. 2) шекаралық шартын қанағаттандырсын.
Олай болса
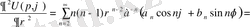
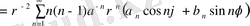
Осы функцияны ρ 2 ға көбейтіп V(ρ, ϕ) арқылы белгілейік, яғни
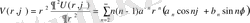
деп белгілеп алайық.
Егер де
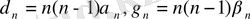 деп белгілеп алатын болсақ, онда
деп белгілеп алатын болсақ, онда
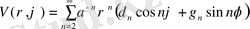
функциясына ие боламыз.
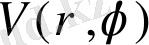 функциясы
ρ< a
аймағында гармониялық болады. (3. 1. 2) шекаралық шартынан осы функциямыздың
ρ = a-
шеңбердегі мәні
функциясы
ρ< a
аймағында гармониялық болады. (3. 1. 2) шекаралық шартынан осы функциямыздың
ρ = a-
шеңбердегі мәні
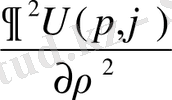 функциясының мәніне тепе тең болады, яғни келесі
функциясының мәніне тепе тең болады, яғни келесі

теңдіктер орынды болады.
Олай болатын болса алдынғы параграфтарда алған нәтижелер бойынша
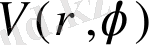 функциясы
ρ< a
аймағында Лаплас теңдеуі үшін ішкі Дирихле есебінің жауабы яғни шешімі ретінде Пуассон интегралымен жазылады.
функциясы
ρ< a
аймағында Лаплас теңдеуі үшін ішкі Дирихле есебінің жауабы яғни шешімі ретінде Пуассон интегралымен жазылады.
Сонымен,
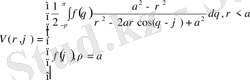
Ендігі ретте негізгі есебіміздің шешімі болатын функцияны, яғни U(ρ, ϕ ) функциясын табайық.
Егер де f(ϕ ) - шеңберімізде берілген функцияны периодты деп есептеп алып оны Фурье қатарына жіктесек, ол жағдайда бұл функция
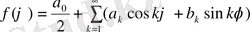
қатары түрінде жазылады. (3. 1. 2) шекаралық шарты бойынша

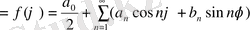
Осы көрсетілген теңдіктерде қатарларымыздың коэффициенттерін теңестіріп, α n , β n белгісіз коэффициенттері үшін
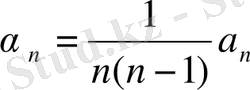 ,
,
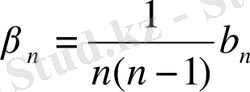 ,
n=2, 3, …,
,
n=2, 3, …,
теңдіктерін шығарып аламыз.
Бұл жердегі
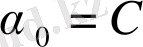
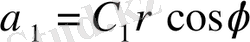 ,
,
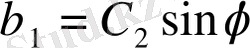
С, С 1 , С 2 -кез келген тұрақтыларболып табылады.
Егер де екі қатарды салыстыратын болсақ, онда
а 0 = а 1 = b 1 =0
болатынын байқаймыз.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz