Скаляр көбейтінді және оның қасиеттері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

15 Скаляр көбейтінді және оның қасиеттері

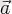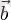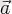
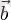
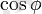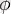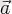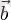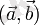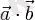$\vec{a}$ мен $\vec{b}$ векторларының көбейтіндісі деп $\vec{a}$ $\vec{b}$ $\cos \phi \,$ тең санды айтады, мұндағы $\phi \,$ - $\vec{a}$ мен $\vec{b}$ векторлары арасындағы бұрыш. Белгілеулері: $(\vec{a},\vec{b})$ немесе $\vec{a}\cdot\vec{b}$ .

Егер векторлардың біреуі нөлдік болса ϕ бұрышының беймәлімдігіне қарамастан көбейтінді нөлге тең боп деп есептеледі.

( $\overrightarrow{a}, \overrightarrow{b) } = \overrightarrow{a}*\left \overrightarrow{b} \right*cos(\overrightarrow{a}\hat{}\overrightarrow{b}) \$

Векторлардың скаляр көбейтіндісінің қасиеттері:

- коммутативтілік.
- дистрибутивтілік.
- санға көбейтуге қатысты сызықтық қасиеті.

1 $\alpha > 0 \rightarrow (\alpha\overrightarrow{a}\hat{}\overrightarrow{b})$ = $\ \overrightarrow{a}\hat{}\overrightarrow{b}(\alpha\overrightarrow{a}, \overrightarrow{b) }$ = $\overrightarrow{\alpha a}*\left \overrightarrow{b} \right*cos\varphi$ = $\ \alpha(\overrightarrow{a, }\overrightarrow{b})$

2 $\alpha = 0\$ , $\alpha\overrightarrow{a}$ =0 $\rightarrow (\alpha\overrightarrow{a}\hat{}\overrightarrow{b})$ = $\ (\overrightarrow{0}\hat{}\overrightarrow{b})$ =0* ${}\left( \overrightarrow{a}, \overrightarrow{b} \right) = \alpha(\overrightarrow{a}, \overrightarrow{b})$

3 $\alpha < 0, \ \ \ \ \ \ \ \ \ \ \ \ \alpha\overrightarrow{a\ }$ ^ $\overrightarrow{b}$ = $\pi$ + $\varphi$

Cos( $\pi$ + $\varphi$ ) =-cos $\varphi$

$(\alpha\overrightarrow{a}\hat{}\overrightarrow{b})$ = $\ \alpha\overrightarrow{a\ }$ * $\overrightarrow{b}$ * Cos( $\pi$ + $\varphi$ ) =(- $\ \alpha) \overrightarrow{a\ }$ * $\overrightarrow{b}$ *(-cos $\varphi) = \ \alpha(\overrightarrow{a}, \overrightarrow{b})$

- вектор нормасы. \ \ \ \ \ \ \ \ \ \

( $\overrightarrow{a}, \overrightarrow{a) } \geq 0$ , ( $\overrightarrow{a}, \overrightarrow{a) } = 0$ $\rightarrow$ $\overrightarrow{a} = 0$

( $\overrightarrow{a}, \overrightarrow{a) } = \left \overrightarrow{a} \right*\left \overrightarrow{a} \right*cos0 = {\overrightarrow{a}}^{2} \geq 0$

${\overrightarrow{a}}^{2} = 0$ $\rightarrow$ $\overrightarrow{a} = 0$

∀a→\forall\overrightarrow{a}\үшін(a→, 0) =a→*0→*cos(a→̂0→) \left( \overrightarrow{a}, 0 \right) = \overrightarrow{a}*\left \overrightarrow{0} \right*cos(\overrightarrow{a}\hat{}\overrightarrow{0}) =0

Геометриялық түрде алғанда скаляр көбейтінді бір вектордың ұзындығын екінші вектордың біріншісінің бағытына ортогональ проекциясының ұзындығын көбейткенге тең. Кез келген 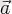$\vec{a}$ векторының бірлік вектормен скаляр көбейтіндісі 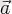$\vec{a}$ векторының сол бірлік векторға ортогональ проекциясы болып табылады. [1]

16 Кесіндіні берілген қатынаста бөлу

Кеңістікте $M_{1}\ {және\ \ M}_{2}\ нүктелерімен\ шектелген\ M_{1}{\ M}_{2}\ кесіндісі\ және\ осы\$

кесіндіде жататын М нүктесі кесіндіні $\aleph$ (лямбда) қатынасында бөлсін.
$\ \ \frac{M_{1}}{{\ M}_{2}\ } = \aleph$ М нүктесінің радиус векторын, онан әрі оның координаталарын табу керек. ${\overrightarrow{r}}_{1}\, \ {\overrightarrow{r}}_{2}$ және ${\overrightarrow{r}}_{}$ арқылы : $\overrightarrow{M_{1}{\ M}_{2}} = \overrightarrow{M_{1}{\ M}_{2}}$ = ${\overrightarrow{r}}_{} - {\overrightarrow{r}}_{1}\ \$

$M_{1}{\ M}_{2} = {\overrightarrow{r}}_{2} - {\overrightarrow{r}}_{1}$

${\overrightarrow{r}}_{} - {\overrightarrow{r}}_{1} = \aleph({\overrightarrow{r}}_{2} - {\overrightarrow{r}}_{1})$

r= $\frac{{\overrightarrow{r}}_{1} + \aleph{\overrightarrow{r}}_{2}}{1 + \aleph}$ x= $\frac{x_{1 +}\aleph x_{2}}{1 + \aleph}$ y= $\frac{y_{1} + \aleph y_{2}}{1 + \aleph}$ z= $\frac{z_{1} + \aleph z_{2}}{1 + \aleph}$ бұл формулалар

кесіндіні берілген $\aleph$ қатынаста бөлу формуласы деп аталады.

17 Базис және өлшем. Вектордың координатасы . Аффиндік координаталар жүйесін анықтау.

Х әріпімен бір түзу бойындағы не жазықтықтағы, кеңістіктегі барлық векторлардың жиынын белгілейік. Х тегі реттелген $e_{1}, e_{2}, \ldots\, e_{k}$ векторлар жүйесі сызықсыз тәуелді болып, ал Хтегі кез келген а векторы осы векторлар арқылы сызықтық өрнектелсе:

$a = \alpha_{1}e_{1} + \alpha_{2}e_{2} + \alpha_{k}e_{k}$ (1)

Онда $e_{1}, e_{2}, \ldots\, e_{k}$ жүйесі Хтің базисі деп аталады. (1) формула а векторының

$e_{1}, e_{2}, \ldots\, e_{k}$ базисі бойынша жіктеуі, ал $\alpha_{1}, \ \alpha_{2}, \ldots\, \ \alpha_{k}\ \$ коэффициенттері а векторының $e_{1}, e_{2}, \ldots\, e_{k}$ базисіндегі координаталары деп аталады. Кез келген вектордың берілген базистегі координаталары бірмәнді анықталады. Екі вектордың бір базистегі сәйкес координаталары бірдей болған жағдайда және тек сол жағдайда тең болады. Векторларды қосқанда олардың сәйкес координаталары қосылады. Векторды санға көбейткенде әр координа осы санға көбейтіледі. Екі вектор коллинеар болуы үшін олардың сәйкес координаталары пропорционал болуы қажетті және жеткілікті. Аффиндік координаталар жүйесі: Теорема1:Берілген түзу бойындағы кез келген екі вектор сызықты тәуелді вектор жүйесін құрайды. Берілген екі вектордың біреуі нөлдік вектор болса, сызықтық тәуелділіктің бірінші қасиеті бойынша бұл вектор сызықтық тәуелді. Егер екі вектор да нолдік вектор болмаса онда олар коллинеар болады.

Егер коллинеар емес $\overrightarrow{а}\ \, \ \overrightarrow{b}\ және\ \ \ \ \overrightarrow{c}\ \ \ үш\ вектор\ үшін\ \ \alpha\overrightarrow{а} + \beta\overrightarrow{b} + \gamma\overrightarrow{c} = \overrightarrow{0}$ теңдігі орындалатын болса, онда $\alpha = \ \beta = \ \gamma = 0$

Анықтама:үш $\overrightarrow{а}\ \, \ \overrightarrow{b}\ және\ \ \ \ \overrightarrow{c}\ \ \$ коллинеар емес вектор бір анықталған ретте алынған болса, онда оларды кеңістіктегі базис деп атайды. Әрі $\overrightarrow{а}\ \ векторын\ бірінші, \ \overrightarrow{b}векторын\ екінші\ және\ \ \overrightarrow{c}\ \ векторын\ үшінші\ базистік\$

векторлар деп атайды. Кеңістіктегі О нүктесі берілсін, ал М нүктесі кеңістіктің $\forall$ нүктесі болсын. Онда $\overrightarrow{ОМ}$ бағытталған кесіндісі М нүктесінің радиус векторы деп, ал берілген МО нүктесі полюс деп аталады. Радиус вектор дегеніміз бас нүктелері полюсте орналасатын бағытталған кесінділер. L түзуінде бір базис пен О полюс берілген болса, онда Lде аффиндік координаталар жүйесі берілген деп есептеледі. М $\in$ L (сәйкес М $\in Р\$ , М $\in$ V) нүктесінің аффиндік координаталары деп $\overrightarrow{ОМ}$ радиус векторы берілген базистегі координаталары деп аталады.

18-19 Кеңістіктегі төрт вектордың сызықты тәуелділігі

Кеңістіктегі сызықты қандай да бір екі беттің қиылысынан пайда болған нүктелердің геометриялық орны деп қарастыруға болады. Егер кеңістіктегі екі бет $F(x, y, z) = 0\ \ \ және\ Ф(x, y, z) = 0$ теңдеуі анықталады деп есептесек, онда олар қандай да бір сызық бойымен қиылысатыны айқын. Олай болса, сол екі беттің теңдеулерін бірге

$\left\{ \begin{array}{r} F(x, y, z) = 0\ \\ Ф(x, y, z) = 0 \end{array} \right. \$ сфералық беттің

$\left\{ \ \ \ \ \ \ \ \ x^{2} + y^{2} \right. \ + z^{2} = R^{2}$ және z=C жазықтығының қиылысында шеңбер болатыны белгілі.

$\left\{ \begin{array}{r} \left\{ \ \ \ \ \ \ \ \ x^{2} + y^{2} \right. \ + z^{2} = R^{2} \\ z = C \end{array} \right. \$

20 Кеңістіктегі вектор ұғымы және оларға қолданылатын амалдар. Қасиеттері.

Жазықтықтағы түзу сияқты кеңістіктегі түзудің де орны сол түзуде жататын бекітілген бір $M_{1}(x_{1}, y_{1}, z_{1})$ нүктесімен сол түзуге параллель бір $\overrightarrow{s} = \overrightarrow{m}i + \overrightarrow{n}$ j+ $\overrightarrow{p}k$ векторы арқылы толық түрде анықталған болады. Түзуге параллель осы $\overrightarrow{s}$ векторы оның бағыттаушы векторы деп аталады. Оның координат осьтеріне проекциясы түзудің бағыттаушы коэффициенттері деп аталады. Сонымен l түзуі сол түзуде жатқан $M_{1}(x_{1}, y_{1}, z_{1})$ нүктесін және бағыттаушы коэффициенттері m, n, p болатын $\overrightarrow{s} = \overrightarrow{m}i + \overrightarrow{n}$ j+ $\overrightarrow{p}k$ бағыттаушы векторы арқылы осы l түзуінің теңдеуін табу қажет.

21 Көпмүшеліктің рационал түбірлері

Егер $\varphi \in P\ мәнін\ \ f\ көпмүшесінің\ айнымалысына\ меншіктегенде\$

$\ f(\varphi) = 0\$ болса, онда $\varphi$ $f$ тің түбірі деп аталады.

Теорема: (Безу теоремасы)

$\varphi$ $f$ тің түбірі болуы үшін $f\ көпмүшесі$ х $\varphi$ көпмүшесіне қалдықсыз бөлінуі қажет.

22. Нақты сандар өрісінде жіктелмейтін көпмүшеліктердің дәрежесі туралы теорема. f(x) = $\alpha_{0} + \alpha_{1}x + \alpha_{2}x^{2} + \ldots + \alpha_{n}x^{n}$

Кез келген f $\in K\lbrack X\rbrack$ көпмүше болсын. f көпмүшесінің дәрежесін degf символымен белгілейміз. Барлық коэффиценттері нөлге тең көпмүше нөлдік көпмүше деп аталады да, 0 символымен белгіленеді. Нөлдік көпмүшенің дәрежесі анықтама бойынша - $\infty$ ке тең деп ұйғарылады, яғниdeg0=- $\infty$ . Егер f-тің кем дегенде бір коэффиценті нөлге теңі емес болып, ал m саны көпмүшенің нөлден өзге коэффиценттерінің ең үлкен индексі болса, онда f көпмүшесі m-дәрежелі, ал $\alpha_{m}$ коэффиценті f-тің бас коэффиценті деп аталады. Бұл жағдайда degf=m деп анықталады.

Көпмүшеліктердің дәрежелері - $\infty$ , 0, 1, 2 . . . мәндерін қабылдайды. Дәрежесі - $\infty$ -ке тең жалғыз ғана көпмүше бар. ол 0 көпмүшесі. Бос мүшесі нөлден өзге, ал басқа коэффиценттері нөлге тең болатын көпмүшелердің дәрежесі 0-ге тең болады. Сонымен $K\lbrack X\rbrack$ -тағы айнымалысыз көпмүшенің дәрежесі 0-ге тең немесе - $\infty$ -ке тең болады.

К жиынының элементтерін дәрежелері нөлден аспайтын көпмүшелер деп есептейміз. Сонымен К жиынын $K\lbrack X\rbrack$ көпмүшелер жиынының ішкі жиыны деп қарастыруға болады. Нақты сандар өрісінде жіктелмейтін көпмүшеліктердің дәрежесі 1-ге немесе 2-ге тең болады. f(x) $\in R\lbrack x\rbrack,$ deg f=n

24. Көпмүшеліктің түбірі. Горнер схемасы. Егер $\gamma \in P$ мәнін f көпм-ң айнымалысына меншіктегенде f( $\gamma$ ) =0 болса $\gamma - f$ -тің түбірі деп аталады. Әдетте әрбір $\gamma \in P$ нөлдік көпм-ң түбірі болады.

1-теорема. (Безу теоремасы) : $\gamma - f$ -тің түбірі болуы үшін f көпмүшесі x- $\gamma$ көпм-е қалдықсыз бөлінуі қажетті және жеткілікті.

Дәлелдеу. f(x) =(x- $\gamma$ ) q(x) +f( $\gamma$ ) . Осыдан f( $\gamma)$ болуы үшін x- $\gamma\ \ f$ қатыстың орындалуы қажетті және жеткілікті.

2-теорема. Көпмүшелердің түбірлерін бөлу амалымен байланыстырады. Оның негізінде түбірдің еселігін енгізуге болады.

f $\neq 0$ болсын. Егер ${(x - \gamma) }^{k}f(x)$ бірақ ${(x - \gamma) }^{k + 1}$ көп-і f көп-н бөлмейтін болса, онда $\gamma$ түбірі k-еселі түбір , ал k саны $\ \gamma$ түбірдің еселігі деп аталады. Егер $\gamma$ түб-ң к еселігі 1-ге тең болса, онда $\gamma$ жай түбір , ал к $\geq$ 2 болғанда еселі түбір д. а. 0 нөлдік көпмүшесі үшін түбір еселік ұғымы анықталмаған. Оның себебі айқын. Кез келген к натурал саны үшін ${(x - \gamma) }^{k}0(x) .$

3-теорема. $\gamma_{1}, \gamma_{2}, \ldots, \gamma_{l} \in p$ еселіктері сәйкес $k_{1}, k_{2}, \ldots, k_{l}$ болатын нөлдік емес f -көп-ң түбірлері болсын. Онда бір g көп-і үшін f(x) = ${(x - \gamma_{2}) }^{k_{1}}{(x - \gamma_{2}) }^{k^{2}}\ldots{(x - \gamma_{l}) }^{k_{l}} \bullet g(x)$ және g( $\gamma_{1}$ ) $\neq 0$ , g( $\gamma_{2}$ ) $\ \neq 0, \ldots g(\gamma_{l}) \neq 0$

Салдар. Нөлдік емес f көпмүшесінің түбірлерінің саны олардың еселігін қоса есептегенде f көпм-ің дәрежесінен аспайды.

Дәлелдеу. P өріс болғандықтан degf= $k_{1} + k_{2} + \ldots k_{l} + \deg{g \geq k_{1} + k_{2} + \ldots k_{l}}$ қатыстарын аламыз.

Горнер схемасы . f= $a_{n} \bullet x^{n} + \ldots + a_{k} \bullet x^{k} + \ldots a_{1} \bullet x + a_{0}$

a $\bullet x + b, \ \ \ \ \ \ \ \ g = x - c$ , берілген f көпмүшесін осы екмүшелікке қалдықпен бөлейік;

f=(x-c) *q+r, 0<=degr<deg(x-c) =1=>degr=0 яғни r=const. degf=n, deg(k-c) =1, degr=0=>degq=n-1.

$a_{n} \bullet x^{n} + \ldots + a_{k} \bullet x^{k} + \ldots a_{1} \bullet x + a_{0}$ =(x-c) ( $b_{n - 1}*x^{n - 1} + \ldots + b_{k - 1}*x^{k - 1} + \ldots + b_{1}*x + b_{0}$ ) + $a_{0}$ ;

$a_{n} = b_{n - 2};$

$a_{n - 1} = b_{n - 2} - b_{n - 1}*c;$

. . . ;

$a_{k - 1} = b_{k - 2} - b_{k}*c;$

. . ;

$a_{1} = b_{0} - b_{1}*c;$

$a_{0} = a - b_{0}*c;$

$b_{n - 1} = a_{n};$

$b_{n - 2} = a_{n - 1} + c*b_{n - 1};$

;

$b_{k} = a_{k + 1} + c*b_{k + 1};$

24 . . ;

$b_{0} = a_{1} + b_{1}*c;$

a= $a_{0} + b_{0}*c;$

Осы формулалар арқылы q(k) көпмүшелігінің коэффиценттері мен қалдықтарының барлық мәндері табылады.

f(x) =(x-c) *q(x) +a, x=c болса =>a=f(c) осылай есептеу алгоритмі Горнер схемасы деп аталады.

25. Көпмүшеліктер сақинасындағы бөлігіштік қасиеттер.

(1) Егер f $g$ және $g$ h болса, онда fh

(2) Егер f $\ g$ және fh болса, онда f ( $g \pm \$ h)

(3) Егер f $\ g$ және h кез келген көпмүше болса, онда f( $g \bullet h)$

(4) Егер f $\ g$ ₁ , f $\ g$ ₂ . . . , f $\ g$ _к және h ₁ , h ₂ . . . h _k -кез келген көпмүшелер болса, онда

f ( h ₁ $\ g$ ₁ +h ₂ $\ g$ ₂ + . . . +h _k $\ g$ _k )

(5) Р өріс болсын, f, $\ g$ $\in$ Р[Х], Егер f $g$ және $g$ f болса, онда Р -ның нөлден өзгеше бір $\alpha$ элементі үшін f= $\alpha \bullet g\ \ теңдігі\ \ орындалады.$

(1) -(4) қасиеттерінің дәлелдеулері бір -біріне ұқсас. Мысалы (2) қасиеттің орындалуын көрсетейік. f $g$ , fh болсын. Онда q ₁ мен q ₂ табылып, $g$ = f $\ \bullet$ q ₁ , h=f $\bullet$ q ₂ болады. Бұдан ( $g \pm \$ h) .

(5) қасиетті дәлелдейік. f $g$ және $g$ f болсын. Егер f пен $g$ -ның біреуі нөлдік көпмүше болса, онда екіншісі де нөлдік болады да $\alpha$ =1 деп ала саламыз.

f пен $g$ екеуі де нөлдік емес болсын. Онда f = $\ g$ $\bullet$ q ₁ және $g$ = f $\ \ \bullet$ q ₂ орындалатындай q ₁ $\bullet$ q ₂ $\in$ Р[Х] көпмүшелері табылады. Осыдан f =f $\bullet$ q ₁ $\bullet$ q ₂ Осы теңдіктегі көпмүшелерінің дәрежелерін теңестіріп degf=degf+deg q ₁ +deg q ₂ , мына deg q _{1 =} deg q ₂ =0 теңдіктеріне келеміз. Осыдан q _1, q ₂ $\in$ Р және q ₁ $\neq$ 0 Демек, $\alpha$ = q ₁

26. ЕҮОБ-тің сызықты өрнектелуі туралы теорема. Егер d=(f, g) болса онда $\exists$ U, V $\in R\lbrack x\rbrack$ және f(x) $\bullet U(x) + g(x) \bullet V(x) = d(x)$ Мұнда deg U degg-degr, degv degf-degr (*)

Дәлелдеуі: d= $r_{m} = r_{m - 2} = r_{m - 1}*q_{m - 1}: = l_{m}\left( r_{m - 2}; \ r_{m - 1} \right) = r_{m - 2}*1 + r_{m - 1}\left( - q_{m} - 1 \right) = l_{m}\left( r_{m - 2}, \ l_{m} \middle r_{m - 3}, \ r_{m - 2} \right) = l_{m - 1}\left( r_{m - 3}; \ r_{m - 2} \right) = \ldots l_{3}\left( r_{1}, r_{2} \right) = l_{3}\left( r_{1}, \ g - r_{1}q_{1} \right) = l_{2}\left( r_{1}, g \right) = l_{2}\left( f - g*q_{0}, g \right) = l_{1}(f, g)$