Л. В. Канторович және сызықты бағдарламалау: тарихы, теориясы және экономикалық модельдеу


Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:
Жоспар
1. Л. В. Канторович және сызықты бағдарламалау. …. 1-6
1. 2 Сызықты бағдарламалау есебінің негізгі түсініктері7-8
2. Экономикалық есептер үшін математикалық үлгілер құру. . …. 9-10
2. 1 Тиімді рацион құру есебі (минимумдеуге берілген сызықты бағдарламалау есебі) . . 11-13
2. 2. Сызықты бағдарламалау есебінің шешімін графикалық түрде табу… . . . 14-16
3. 1 Сызықты бағдарламалау есебін графикалық әдіспен шығару мысалдары. 15-20
Л. В. Канторович және сызықты бағдарламалау
Л. В. Канторович 1912 жылдың 19 қаңтарында Санкт-Петербург
қаласында дәрігерлер жанұясында дүниеге келді. 1926 жылы 14 жасында, ол
Ленинград университетіне оқуға түседі. Сол кездегі Ленинград университетінде қалыптасқан жақсы математикалық орта бар болатын. Көп ұзамай Л. В. Канторович студенттерге арналған белгілі математик Г. М. Фихтенгольцтің жетекшілігімен ұйымдастырылған үйірмеге қатыса бастайды. Профессор Г. М. Фихтенгольцтің Математикалық талдау курсына арналған оқулықтары осы күнге дейін жоғары оқу орындарында қолданыс табуда. 1930 жылы ЛМУ -ді бітірген ол, Ленинградтың оқу орындарында сабақ бере жүріп ғылыми зерттеулермен де айналысады. Ғылыми зерттеулерінде үлкен жетістіктерге жетіп, 1932 жылы Ленинградтың азаматтық құрылыс инженерлерін дайындау институтында профессор атағын, ал 1934 жылы ЛМУ профессорлығын алады. Өзі қатысқан Г. М. Фихтенгольцтің математикалық үйірмесі Л. В. Канторович- Фихтенгольцтардың ғылыми семинарына айналады. Ол математиканың көптеген салаларынан жаңалық ашқан белгілі ғалым ретінде танылады. Өз өмірінде 300 - ден астам ғылыми еңбектер жазған ғалым, еңбектерін мынадай тоғыз тарауға жіктеп қарастыруды ұсынады [1] :
1) функцияның дескритивті теориясы және жиындар теориясы,
2) функцияның конструктивті теориясы,
3) талдаудың жуықтау әдістері,
4) функциональдық талдау,
5) функциональдық талдау және қолданбалы математика,
6) сызықты бағдарламалау,
7) есептеуіш техника және бағдарламалау,
8) тиімді жоспарлау және тиімді бағалар,
9) жоспарлы экономиканың экономикалық проблемалары.
Бастапқы тараулар 1 -4 көбірек теорияға жақын болса, соңғы 5 -9
тараулары қолданбалы жағына жақынырақ. Бірақ, өзі атап көрсеткендей
ғылымның өзінде іштей бірлік бар, математика мен экономиканың жан - жақты теориялық және қолданбалы проблемаларын шешуге қажетті идеялар мен өзгерістердің бір-біріне бойлай енуі орын алады. Оның шығармашылығына тән ерекшелік сол кездегі математика мен экономиканың ең ауыр проблемалары мен болашаққа бағытталған алдыңғы қатарлы идеяларының өзара байланыстылығы. Сондай проблемалардың бірі сызықты бағдарламалау есебі . Кезінде - «өміріңіздегі ең маңызды ғылыми жетістігіңіз не деп есептейсіз деген сұраққа » - ол сызықты бағдарламалау деп, жауап берген. Сызықты бағдарламалаудың пайда болу тарихы мен оның байланыстарына қысқаша тоқталайық.
Сызықты бағдарламалау . Күнделікті өмірде әр түрлі шешімдер ішінен,
мүмкін болатын ең дұрыс шешімді таңдап алуға тура келеді. Оны тиімді
шешім - деп те атайды. Мұнда біз қолда бар құралдар мен қорлардың әр
уақытта жеткілікті бола бермейтінін ескеруіміз керек. Аз мүмкіндіктерді
пайдалана отырып, үлкен жетістіктерге жету үшін жоспар , немесе
әрекеттердің бағдарламасын құру қажет. Оны ғылыми тұрғыдан тиянақтау
үшін XX - шы ғасырдың орта шенінде арнайы математикалық аппарат
құрылды. Математиканың бұл тарауы математикалық бағдарламалау деп
аталды. Мұндағы прогаммалау сөзін ЭЕМ- да программа құрумен шатастырмау керек. Ол кейін пайда болған сызықты бағдарламалау, серпінді бағдарламалау т. с. с. түсініктер мен ұштасып жатыр. Сызықты бағдарламалау пайда болған уақыты 1939 жылы Л. В. Канторовичтің “ Өндірісті ұйымдастыру мен жоспарлаудың математикалық әдістері” атты кітабының шыққан уақытымен байланыстырылады. Канторовичтің келтірген математикалық әдістері қолмен есептеуге жарамсыз болды, ал тез есептейтін қазіргі заманғы есептеуіш машиналар жоқ болды. Сондықтан оның жұмыстары біршама уақыт ескерусіз қалды. Екінші жағынан Канторовичтің экономикаға қатысты бұл еңбегі көптеген ғалымдар жағынан түсінік таппай, оған жалған ғылым сияқты көзқарас қалыптасты. Канторовичке экономикадағы математиканы қолдану бағытындағы жұмыстарын уақытша тоқтата тұруға тура келді.
Сызықты бағдарламалаудың өмірге қайта келуін 1950 - ші жылдардың бас
кезінде ЭЕМ- ның пайда болып, жедел қолданысқа енгізілумен байланыстыруға болады. Леонид Витальевичтің концепциясы соғыстан кейінгі жылдары қайта ашылды. Америкалық экономист Т. Купманс біршама жылдар бойы математик ғалымдардың назарын әскери тақырыптарға қатысты ұшақтардың ұшу кестесін құру, қорларды таратып орналастыру т. б. проблемаларға аударды. Нәтижесінде математикалық ұжым құрылып, көп-жақтардағы сызықты теңсіздіктермен берілген сызықты функциялардың экстремумын табу есептерін қарастыра бастады. Математиканың бұл тармағы Т . Купманстың ұсынысымен (1951ж) сызықты бағдарламалау деп аталды. Кейін операцияны зерттеу, математикалық экономика, экономикалық кибернетика сияқты аттармен белгілі болып, тарала бастаған сызықты бағдарламалау-сызықты тиімділік үлгілерін зерттеуге, яғни тиімді мәндері табылуы қажет есептерді шығаруға, теориялық және сандық талдаулар жүргізуге арналған. Мұндағы үлгілер зерттелетін объектілер мен үрдістердің, құбылыстардың ең маңызды жақтарын, белгілерін көрсетуге мүмкіндік береді. Тиімділік немесе экстремум мәндер табу - максимум немесе минимум мәндер табу. Зерттелетін үрдіс қандай бір болмасын теңсіздіктер жүйесімен сипатталады.
АҚШ- та сызықты бағдарламалау 1947 жылдан бастап, Дж Данциг - еңбектерінде қалыптаса бастады. Ол, кейін симплекс әдіс деген атақ алған
сызықты бағдарламалау есептерін шығарудың қолдануға жеңіл, сандық әдісін
ойлап тапты. Қойылған кедергілерге қарамастан Л. В. Канторович та
экономикалық идеяларға құрылған математикалық жұмыстарына қайта
оралып, Д. Ж. Данцигтен тәуелсіз симплекс әдістің идеясына келді. Оның бұл
еңбектерін жоғары бағалаған Д. Ж. Данциг «Канторович өндіріске қатысты
есептердің үлкен, маңызды класын математикалық тұрғыдан сипаттауға көз
жеткізген бірінші адам болды. Оның ойынша бұлай сипаттау есепке сандық
тұрғыдан қарауға және оны сандық әдістермен шығаруға мүмкіндік
береді. Канторович алғашқы табылған мүмкін шешімді пайдалануға
негізделген әдісті сипаттады . . . » -деп, өзінің сызықты бағдарламалаудың
тарихына арналған еңбегінде атап өтті.
Л. В. Канторовичтің экономикалық жаңалығын қысқаша - тиімді шешім мен тиімді бағаның өзара тәуелділігі деп тұжырымдауға болад ы.
Леонид Витальевич 1957 жылғы Ғылым Академиясының Сібір бөліміне
жұмысқа ауысады. Осы кезден бастап ол экономикалық немесе онымен
байланысты математикалық проблемалармен айналысып, бұрынғы жасалған
жұмыстарын ашық түрде жалғастыруға мүмкіндік алды. Бұрын
жарияланбаған еңбектері де жарық көре бастады. Оның ішінде «Қорларды
пайдаланудың ең жақсы экономикалық есептеулері » кітабы да бар. Осы
жасалған еңбектері Кеңестер Одағында В. В. Новожилов және В. С. Немчиновтармен бірге 1965 жылы Лениндікпен сыйлықпен , ал 1975 жылы
М Купманспен бірге Нобель сыйлықтарымен марапатталады.
Сызықты бағдарламалау идеяларының қарышты дамып, қолданысқа ене
басталғаны соншалық, қазір экономика мамандығын алған кез келген
студентке таныс. Ол Қазақстанның университеттерінде оқытылып жүрген
«Экономикалық- математикалық әдістер» пәнімен тікелей байланысты.
Өтілетін негізгі:
1. Сызықты бағдарламалауға келтіретін өндіріске қатысты есептер. Сызықты модельдер.
2. Сызықты бағдарламалау есебінің жалпы қойылуы. Дөңес көпжақтар және сызықты теңсіздіктер.
3. Симплекс әдістің теориясы.
4. Екі жақтылық симплекс әдіс.
5. Сызықты бағдарламалаудың арнайы есептері. Көлік қатынасы есебі. Көлік қатынасы есебінің потенциалдар әдісі.
6. Салааралық баланс. сияқты тақырыптар экономист мамандарға математиканың экономикада қолданылу мүмкіндіктерінің кең екендігін көрсетіп, нарықты экономикада тиімді жоспарлар құрып, оның шешімдерін нақты табуға мүмкіндік жасайтынын көреміз. Пәннің атынан байқалғандай экономикалық - математикалық ағартуға, нәтижесінде экономика - математикалық мәдениет түсінігін қалыптастыруға келеміз. Мұндағы математика фундаменталь және қолданбалы зерттеулердің негізі болып табылады. Сондықтанда математикалық пәндер « Математика» мен «Информатика» мамандықтары студенттерінің ғана кәсіби біліктілігін қалыптастыруға ғана емес, сонымен қатар «Экономика» мамандығы студенттерінің де кәсіби біліктілігін қалыптастыру үшін өте маңызды.
«Экономика» мамандығында оқитыны студенттердің экономикалық
мәдениеті I-II курстарда өтетін «Экономикалық теория», «Экономикалық
ғылымдар тарихы», «Экономикалық білімдер негіздері», «Макроэкономика», «Микроэкономика» сияқты пәндер өтуі кезінде қалыптасады. Онда көптеген экономикалық үрдістердің үлгілері түсініктерімен танысады. әр түрлі деңгейдегі тапсырмалар алып, есептер шығарады. Тәжірибе көрсеткендей осы пәндерден көптеген түсініктер жете түсінбей қабылданады. йткені, ЭМӘ (экономикалық- математикалық әдістер) пәнінің басқа пәндердің арасындағы алатын орны туралы әлі зерттеулер жүргізіліп, оған деген жаңа көзқарас Қазақстан Республикасының оқу орнындарында қалыптасқан жоқ. Мұнда бірнеше мәселелерге түбегейлі көңіл бөлу керек деп есептейміз.
1. Пән аралық байланыстар . Әсіресе “Экономика” мамандығы студенттеріне оқылатын: Экономикадағы математика, Информатика,
Эконометрика, Ықтималдық теориясы мен статистика- пәндері.
Болашақ мамандардың математикалық мәдениетін қалыптастыру
“ Экономикадағы математика ” пәнінен басталады. Математикалық аппарат - экономикалық талдау ұйымдастыру және басқарудың маңызды құралы. Сондықтан да, оны оқылатын математиканың түсініктерінде экономика, қаржы, басқаруға қатысты қолданбалары жағына көңіл аударылып отыру керек. Осы жерде математиканы оқытудағы қолданбалы бағыт түсінігіне келеміз. Көптеген зерттеушілер қолданбалы бағытты жүзеге асырудың негізгі құралы есептер екенін атап өтеді [2] . Ал, экономикалық мазмұнды есептер математикалық аппарат қолданылатын қолданбалы есептердің маңызды түріне жатады.
Нақты объектілер өте күрделі, сондықтан да оларды зерттеу үшін, зерттелетін нақты оъектінің көшірмесі, яғни үлгісі құрылады. Үлгі неғұрлым сәтті таңдап алынып, құрылған болса, соғұрлым нақты объекті туралы дәл ақпарат алуға, мүмкіндік береді. Ғылыми зерттеулерде натурал, физикалық, абстрактілі және математикалық сияқты үлгілер жиі пайдалынады. Математикалық үлгілер құру - математикалық үлгілеу деп аталады. Математикалық үлгілерді пайдалану арқылы математика ғылыми зерттеулерде, ғылымның барлық салаларында, оның ішінде экономика ғылымы да бар қолданыла бастады. Ақпарат, объект, жүйе, алгоритм, формальдау және үлгілеу, программа түсініктері Информатика пәнінің негізгі маңызды түсініктері болып табылады [3] .
Бұдан үлгілеудің негізгі қалыптасуы Информатика пәнінде екендігін көруге болады. Жоғарыда келтірілгендей ЭЕМ дамуы экономикадағы тиімділік есептерінің шешімдерін табуда маңызды роль атқарды. Сол сияқты
“ Экономика” және “ Ықтималдық теориясы мен статистика ” пәндерінің
байланыстарына да тоқталуға болады. Олардың бәрі де сызықты бағдарламалау есептерін терең талдауға мүмкіндік береді.
2. ЭМӘ пәнінің өзінде өтетін тақырыптардың нақтылануы, яғни болашақ
мамандардың экономика - математикалық мәдениетін қалыптастыруға қатысты тақырыптардың бір жүйеге келтірілуі және әр тақырыптар бойынша мақсаттар қоя білу:
- Сызықты бағдарламалаудың тиімділік есептерінің математикалық
үлгілерінің жіктемелерін білу;
- Сызықты бағдарламалаудың тиімділік есептерінің математикалық үлгілерін
құруды игеру;
- Сызықты бағдарламалау есебін канондық түрге келтіруді игеру;
- Сызықты бағдарламалау есебін векторлық түрде жазуды игеру;
- Сызықты бағдарламалау есебін n=3, n=2, k≤ 2 мәндері үшін прафикалық әдіспен шығаруды меңгеру;
- сызықты бағдарламалау есебі шығару үшін симплекс - әдісті қолдануды меңгеру;
- Жасанды базистер әдісін қолдануды біліп, оны бастапқы бұрыштық нүктені табуға қолдануды меңгеру;
- Сызықты бағдарламалаудың бастапқы есебіне екіжақтылық есебін құруды игеру;
- Минимум мән туралы 1- ші және 2 - ші теоремаларды айта біліп, оны сызықты бағдарламалау есебін шығаруға қолдана білу;
- Екі жақтылық симплекс - әдістің қолданылу ерекшеліктерін меңгеру;
- Сызықты бағдарламалау есебін шығарудың кері матрица әдісін меңгеру;
- Көлік қатынасы үлгісі негізінде сызықты бағдарламалаудың арнайы есептері туралы мағлұматы болу;
- Балансқа келтірілген және келтірілмеген көлік қатынасы үлгілерінің шығарылу ерекшеліктерін білу;
- «Солтүстік - батыс» бұрышы әдісін көлік қатынасы есебіне қолдана білу;
- Фогель әдісін көлік қатынасы есебіне қолдануды игеру;
- көлік қатынасы есебінің тиімді жоспарын табуға потенциялдар әдісін колдануды игеру;
- көлік қатынасы үлгілеріне келтірілетін экономикалық есептер туралы мағлұматы болу ( тағайындау есебінің мысалы негізінде) ;
Бұл тақырыптарды Баланстық үлгілер тақырыбына қатысты түсініктер толықтырады:
- салааралық баланстың жалпы сұлбасын және оның негізгі төрт ширектерінің мазмұндарын білу;
- тура және толық материальдық шығындар коэффициентерін есептей білу;
- тура және толық еңбек сыйымдылығы коэффициентерін, қор сыйымдылығы коэффициентерін есептей білу;
3. Қарастырылатын тақырыптарды олардың шығу тарихымен байланыстырып өту. Шынында, тиімділік есептері немесе экстремаль есептердің мыңдаған жылдық тарихы бар [4] . Ал экономикадағы тиімділік есептерімен өткен ғасырдың орта шенінде жаппай айналыса бастады. Соның бір мысалы, Канторовичтің оқушыларымен бірге құрған жеңіл машиналармен жолаушылар тасудың математикалық үлгісі. Оны пайдалану нәтижесінде тасымалдаумен айналысудың тиімділігі артты. әсіресе қысқа қашықтыққа тасымал жасаудың тиімділігі артатыны дәлелденді.
Сондай - ақ көлік қатынасы есебі де, бұрынғы Кеңестер Одағында
алғашқы қолданыс тапқан есептердің бірі. Мысалы, 1959 жылы Москваның 8
өзен порттарына жүк тасымалданатын 209 тұтынушыларын бекітіп, тиімді
жоспар құру нәтижесі мықты экономикалық жетістіктерге қол жеткізген.
Көптеген есептердің шығарылып дамуына олардың әскер істерінде пайдаланылуы себепші болған т. с. с.
4. Экономикалық мазмұнды есептерді шығаруға компьютерлік техниканы
пайдалануға жете көңіл бөлу. Мұнда екі жақты пайдалылық бар. Біріншіден,
студенттердің компьютерлік технологияны пайдалану дағдысы артады да,
өздерінің болашақ мамандықтарына пайдалану ерекшеліктерін қалыптастыра
береді. Екіншіден, айнымалылар саны көп, көп параметрлі экономикалық
есептердің үлгілерін қарастыру арқылы студенттерге сызықты бағдарламалауда қолданылатын экономика - математика әдістерін жете түсіндіруге мүмкіндік туындайды. Қоданбалы бағыттағы есептерді көптеп шығарып салыстыруға мүмкіндік алады.
5. Мектеп математика курсында тиімділік есептерінің алатын орнын анықтау.
Бұл бағытта Ресейде бұрынғы Кеңес дәуірінен бастап жүргізіліп келе жатырған академик В. М. Монахов пен оның ғылыми педагогикалық мектебінің еңбектерін атауға болады. Мұнда сызықты бағдарламалаудың кәзіргі нарықты экономикадағы орнын аша түсетін «Ойындар теориясы» ,
«Операцияларды зерттеу » сияқты курстармен байланыстары да ұзақ
жылдардан бері жете зерттеліп келеді. Педагогикалық институттардың
математика және информатика мамандығы студентеріне аталған курстардың
оқытылу әдістемелерін зерттеп, экономика - математикалық әдістерді
пайдалану мадениетін қалыптастыру мектеп математика курсында алған
білімдерін де пайдалану ерекшеліктері қарастырылуда [2] . Қысқаша мақалада сызықты бағдарламалаудың математиканың функциональ және дөңес талдаулар, дискретті математикамен, вариациялық есептеулер және Лагранжа көбейткіштерімен, ықтималдық теориясы, Марков процестері, жуықтап есепетеулермен т. б. байланыстары қарастырылмай қалды. Жоғарыда айтылғандардан, бастауын 1938 жылы Л. В. Канторовичке фанер тресінің қойған ресурстарды тиімді пайдалану есебінен алған сызықты бағдарламалаудың немесе экономикадағы математиканың XX ғасырдағы ғылым тарихының жарқын беттерінің бірі және математиканың ажырамас бөлігі екенін көреміз. Ол Қазақстанның математика және экономика
ғылымдарында өз орнын табуда.
Сызықты бағдарламалау есебінің негізгі түсініктері
Сызықты бағдарламалау есебі деп, бірнеше айнымалының
сызықты функциясына, ол айнымалыларға қойылған сызықты шектеулер
жағдайында функцияның экстремумын (max немесе min) іздеу есебі ұғылады.
Мысал: Берілген
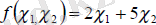
функциясының максимум мәнін, 1 c және 2 c айнымалыларына қойылған келесі шектеулерден табу керек:
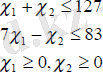
келтірілген сызықты бағдарламалау есебі екі айнымалының теңсіздік-шектеулермен берілген максимумдеу есебі. Теңсіздік шектеулер орнында теңдік-шектеулер де болуы мүмкін.
Сызықты f -функциясы мақсат функциясы , немесе мақсатты функция деп аталады.
Шектеулер:
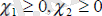 теріс еместік шектеулері
(немесе
теріс еместік шарттары
), ал
сызықты теңсіздіктер және теңдеулер жүйесі сызықты бағдарламалау есебінің шектеулер жүйесі
деп аталады.
теріс еместік шектеулері
(немесе
теріс еместік шарттары
), ал
сызықты теңсіздіктер және теңдеулер жүйесі сызықты бағдарламалау есебінің шектеулер жүйесі
деп аталады.
Теңсіздік шектеулермен берілген сызықты бағдарламалау есебі мына түрде жазылады:
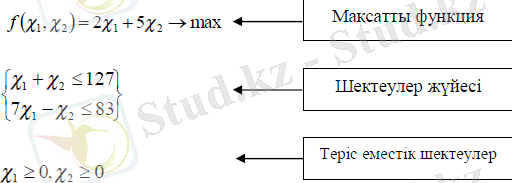
Сызықты бағдарламалау есебі көптеген экономикалық есептер (өндірісті жоспарлау, ресурстарды пайдалану, көлікпен тасымалдау және т. б. ) үшін ыңғайлы математикалық үлгі болып табылады. Бірқатар экономикалық есептер үшін математикалық үлгілер құру процесін мысалдармен қарастырайық . Олар максимум мен минимумге берілген сызықты бағдарламалау есебі түрінде келтіріледі. Осы жерде өткен дәрісте келтірілген үлгі және математикалық үлгілеу (моделдеу) түсініктерін еске түсіруге болады. Үлгі - бұл түп нұсқаны ауыстыратын және оның зерттеуге қатысты маңызды сипаттары мен қасиеттерін бейнелейтін объект. Әрі қарай:
Матеметикалық қатынастардың жиынтығын көрсететін үлгі математикалық деп аталады. Біз оқитын пәнді математикалық экономиканың бір тармағы деп қарастыруға болады. Ал, математикалық экономика - нақты экономикалық объектілердің математикалық үлгілерін зерттейді.
Келесі түсінік: Математикалық экономиканың әдісі - бұл экономиканы күрделі серпімді жүйе ретінде- жүйелік талдау. Басқаша айтқанда өткен дәрісте қарастырылған талдау түсінігінің қажеттілігіне келеміз.
Жүйе - өзара байланыстағы белгілі -бір мақсатты жүзеге асыратын
элементтер бірлестігі. Олар экономикадан тыс болуы немесе ішкі жүйелер
болуы мүмкін. Экономикада кездесетін есептерде әсіресе өндірісті жоспарлауға байланысты есептерде ең тиімді вариантты іздейтін экстремалды есептер қарастырылады. Мұндай есептерде параметрлер саны көп болуы нәтижесінде есептеулер жүргізу қиындыққа түседі. Сондықтанда әртүрлі математикалық әдістер ізделіп, есептеу машинасын пайдалану мүмкіндіктері қарастырылады.
Экономиканы математикалық модельдеудің үш негізгі этаптарын атап өтуге болады:
1. зерттеулердің мақсаты анықталып, есептердің қойылымы анықталады
және де объектіні сапа жағынан экономикалық модель ретінде сипаттау
жүргізіледі.
2. зерттелетін объектінің математикалық моделі қалыптасады, алғашқы
ақпараттар дайындалады.
3. математикалық модельге талдау жүргізіледі, алынған тнәтижелер өңделіп
талданады.
ЭЕМ қолдау көптеген жоспарлардың варианттарын салыстырып, басқаруға
қатысты шешімдер таңдауға мүмкіндік береді.
Экономикаға қатысты математикалық үлгілердің жай мысалдарына тоқталайық.
Экономикалық есептер үшін математикалық үлгілер құру.
Экономикалық моделдерді сызықты бағдарламалау есебі түрінде құрудың негізі экономикалық есептердің параметрлерін дұрыс таңдауға келтіреді. Сонда қажетті мақсат сызықты мақсатты функция түрінде өрнектеледі де, ал процесстерге шектеулер сызықты теңдеулер немесе теңсіздіктер түрінде жазылады. Экономикада кездесетін бірнеше есептер қарастырып, олардың математикалық моделдерін құрайық .
3. 3. 1. Өнім өндіруді жоспарлау есебі ( максималдауға берілген сызықты бағдарламалау есебі) .
Есеп 1. Қандайда бір болмасын өндіріс жоспарлы мерзімде 2 түрлі өнімдер
шығарады. Мысалы: орындықтар және үстелдер. Оларды өндіру үшін
ресурстардың үш түрі пайдаланылады. Әрбір өнімді шығаруға кететін шығын, ресурстар қоры және де өнім бірліктерін шығарудан түскен табыс келесі кестеде келтірілген.

Шығарылатын орындықтар мен үстелдердің санын, берілген шарттар
шегінде, түсетін табыс ең үлкен (max) болатындай етіп, жоспарлау керек.
Сонымен есептің негізгі мақсаты ең көп (max) табыс табу. Өнім шығару
жоспарын сипаттайтын параметрлер ретінде:
1) Шығарылатын орындықтар санын алайық. Оны -айнымалы арқылы
өрнектейік.
2) Шығарылатын үстелдер санын- арқылы белгілейік.
Сонда таңдап алынған белгісіздер арқылы барлық өнімді өткізуден алынған
қосынды табыс
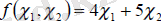
- түрінде жазылады.
Онда барлық орындықтарды өткізуден алынған табыс
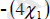 және үстелдерден алынған табыс
және үстелдерден алынған табыс
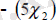
Есептің мақсаты, яғни табысты максималдау былай жазылады
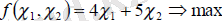
Шектеулерді анықтауға көшейік. Барлық шектеулердің құрылымы бірдей:
Ресурс шығыны ≤ Ресурс қорынан
Енді ресурстардың толық шығындарын және айнымалылары арқылы
өрнектеуге көшейік. Бірінші ресурстан барлық орындықтар шығаруға 4
бірлік, ал барлық үстелдерді шығаруға 6 бірлік кетеді (кестедегі бірінші
жолды қара) . Екеуінің қосындысы бірінші ресурстың толық шығынын береді,
ал шектеу сызықты теңсіздік түрінде жазылады.
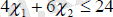
Осылайша, екінші және үшінші ресурстар үшін
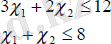
теңсіздіктерін аламыз. Бәрін қосып
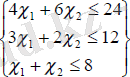
- жүйесін аламыз да, оған теріс еместік шартын тіркеп жазамыз:
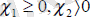
Сонда, қойылған есептің математикалық моделі - сызықты бағдарламалау есебі түрінде былай жазылады:
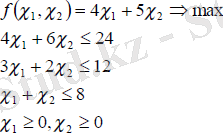
Алынған үлгі өндіру шарты өзгергенде де, өнімді өткізу шарты өзгерген кезде де өзгеріп тұрады. Мысалы, өткізу шарты өзгерген кезде мақсатты функцияның коэффициенттері де өзгереді.
Ресурс қорлары өзгерсе- шектеулер жүйелерінің оң жақтары өзгереді,
өндіріске қатысты жаңа шарттар қосылса, онда шектеулер жүйесіне жаңа
теңдеулер мен теңсіздіктер қосылады.
Сызықты бағдарламалау есебі нің шешімі табылғаннан кейін мен айнымалылары max
табыс келтіру үшін жоспарлау қажет орындықтар мен устелдер санын
көрсетеді.
Теңсіздіктердің оң жағы мен сол жақтарының айырымдары әрбір ресурс түрлерінің қалдықтарын көрсетеді.
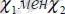 айнымалыларының мәндерін табу үшін сызықты бағдарламалау есебін әр түрлі әдістермен шығарады. Мысалы: геометриялық әдіс, симплекс - әдіс, М- әдіс (жасанды базистер әдісі), т. с. с.
айнымалыларының мәндерін табу үшін сызықты бағдарламалау есебін әр түрлі әдістермен шығарады. Мысалы: геометриялық әдіс, симплекс - әдіс, М- әдіс (жасанды базистер әдісі), т. с. с.
Тиімді рацион құру есебі (минимумдеуге берілген сызықты бағдарламалау есебі)
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz