Еркін ағыстағы акустикалық әсердің шекаралық қабаттың турбуленттікке өтуі мен жылулық сипаттарына әсері: теориялық және эксперименттік зерттеу


Мазмұны
Кіріспе
Бөлім 1. Еркін ағыстағы ағынның сипаттамасына акустикалық әсердің ықпалына және ағыстың еркін шекаралық қабатта турбуленттікке өтуіне шолу жасау.
§1-1. Ағынды орнықтылықтың сызықтық теория шеңберінде зерттеу туралы түсінік.
§1-2. Құйын өсуінің сызықтық емес теориясы негізінде ауысу құбылысын қарастыру.
§1-3. осесимметриялық ағынның бастапқы және соңғы бөліктеріне ағыстың периодтық структурасының әсері.
1. 4 Еркін ағыстың сипатына сыртқы акустикалық әсердің ықпалы.
§1. 5. Аз қыздырылған өске симметриялы ағынның жылулық сипаттамасы.
2 бөлім. Тәжірибелік бағыттар, аппаратура және өлшеу әдістері
§2. 1 Тәжірибелік қондырғының сипаты және ағыс суретіне шолу.
§2. 2 Аппаратура және жылдамдық пульсациясын өлшу әдістемесі.
§2. 3 Аппаратуралар мен орташа және пульсациялық температураны өлшеу әдістері.
ІІІ бөлім. Ағынның жылулық сипатына акустикалық әсердің ықпалы.
§3. 1. Ағын өсі бойындағы орташа және пульсациялық сипаттамалар.
§3. 2. Ағынның көлденең қимасының орташа және пульсациялық сипаттамалар.
§3. 3 Кеңістіктік және бір нүктелі корреляцияларды өлшеу.
§3. 4. Ағынға нейтралды жиілікпен әрект ету.
4-бөлім. Фазалық таңдау әдісі бойынша бастапқы бөліктегі ағынның структурасын эксперименттік түрде зерттеу.
§4. 1. Температураның сынама өлшемін алу.
§4. 2. Құйындар қозғалысының фазалық жылдамдығын анықтау.
§4. 3. Құйындағы жылдамдықты өлшеу.
§4. 4 Құйындағы температураның таралуы.
Кіріспе
Турбуленттік ағыстың қарқындылығы бастапқы және соңғы ағыстың өту шартына және сырқы орта әсеріне байланысты. Сыртқы орта әсерін процестермен басқаруға болады. Ағыстың құрылымына қарқынды әсер ететін әдістердің бірі ағыстың соңғы бөлігіне бойлық акустикалық толқынды қою болып табылады. Дыбыстық толқындардың жиілігіне байланысты жылдамдықтың турбуленттік пульсациясының күшеюі немесе бәсеңдеуі, орташа жылдамдықтар өрісінің қайта орналасуы және ағынның ұзақтығының өзгеруі орын алады.
Сыртқы орта әсерінен турбуленттік қозғалыстың күшеюі немесе бәсеңдеуі көптеген құрылғыларды пайдалануға жол ашады. Мысалы химиялық технологияда және ағындық аппараттарды құрастыру мен пайдалануда және сонымен қатар физикалық құбылыстарды түсінуде маңызды рөл атқарады.
Бірақ қарастырылған тәжірибелер тек ағынның бірнеше аэродинамикалық сипаттамаларын ғана қамтиды. Бұл жұмыста акустикалық әсердің еркін ағынның бастапқы және соңғы бөліктерінің температура өрістеріне ықпалы қарастырылған. Ағынның құйынды құрылымын меңгерудің тәжірибелік әдісі құрылып сыннан өткізілді, сонымен қатар ағынның бастапқы бөлігінде құйынның пайда болу құрылымы қарастырылды.
Бөлім 1. Еркін ағыстағы ағынның сипаттамасына акустикалық әсердің ықпалына және ағыстың еркін шекаралық қабатта турбуленттікке өтуіне шолу жасау.
§1-1. Ағынды орнықтылықтың сызықтық теория шеңберінде зерттеу туралы түсінік.
О. Рейнольдс 19-шы ғасырдың соңғы ширегіде ламинарлық ағыстың турбуленттікке ауысу құбылысын анықтады. Тәжірибелік және теориялық зерттеулер әлі күнге дейін жалғасуда, өйткені турбуленттік ағынның пайда болу теориясы өте күрделі. Ламинарлық шекаралық қабаттың тұрақсыздығының себебі қондырғының камерасындағы және аэродинамикалық құбырлардағы акустикалық шу, вибрация және басқа да сыртқы факторлар. Алайда, Тұрақсыздықтың әрі қарай артуы Рейнольдс санына байланысты. Егер Re шектік
 аз болса, онда шекаралық қабатта пайда болатын аз ғана ауытқу өшеді, ал Re≥
аз болса, онда шекаралық қабатта пайда болатын аз ғана ауытқу өшеді, ал Re≥
 болса күшейеді және нәтижесінде ағыс турбуленттікке ауысады. Ал Рейнольдстің шектік мәні ағынның таралуына байланысты, яғни қысымның градиентіне, шекаралық қабаттың қалыңдығының жасанды жолмен өзгеруіне, жылу берілімдерге.
болса күшейеді және нәтижесінде ағыс турбуленттікке ауысады. Ал Рейнольдстің шектік мәні ағынның таралуына байланысты, яғни қысымның градиентіне, шекаралық қабаттың қалыңдығының жасанды жолмен өзгеруіне, жылу берілімдерге.
Шекаралық қабатта ламинарлық ағыстың турбуленттікке ауысуын 5 бөлікке бөліп қарастыруға болады:
1. тұрақты ағыс алаңы
2. Толлмин-Шлихтинг толқынының пайда болу және өсу аймағы
Ол ағынның тұрақсыздығынан туады
3. үшөлшемді Бенни-Лин толқынының пайда болуы және өсу аймағы
4. құйынның пайда болу аймағы және екіөлшемді тұрақсыздықтың өсуі
5. турбуленттік дақ Эммонстың пайда болу аймағы және жетілген турбуленттік ағынға көшу аймағы.
Бірінші және екінші аймақтар гидродинамикалық тұрақтылықтың сызықтық теориясымен толық сипатталады. Бұл теория шекаралық қабаттағы ағынға байланысты, яғни ламинарлық ағыстың шексіз аз ауытқуы кеңістік бойынша немесе уақыт бойынша өсетінін немесе өшетінін анықтайды. Еркін шекаралық қабаттағы тұрақсыз ағысқа байланысты қысқаша шолу жасайық.
Ағындағы жылдамдықты және қысымды пульсациялық шама ретінде алайық:
(1. 1)
Мұнда <U>, . Құйынды өріс үшін жеке тербелістің ток функциясын берейік
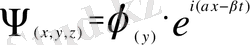 (1. 2)
(1. 2)
Мұндағы
-құйынның комплекстік амплитудасы,
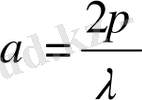 - толқындық сан,
- толқындық сан,
 -толқын ұзындығы. Сұйықтың жазық қозғалысына арналған Навье-Стокс теңдеуі Орра-Зоммерфельд теңдеуіне ауысады
-толқын ұзындығы. Сұйықтың жазық қозғалысына арналған Навье-Стокс теңдеуі Орра-Зоммерфельд теңдеуіне ауысады
 (1. 3)
(1. 3)
Бұл теңдеудіз ерттеу тұрақтылықтың сызықтық теориясы негізінде жүргізіледі. Мұндағы
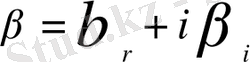 ,
- комплекстік шамалар, мұндағы
-шеңберлік жиілік,
-тербелістің фазалық жылдамдығы,
,
- комплекстік шамалар, мұндағы
-шеңберлік жиілік,
-тербелістің фазалық жылдамдығы,
және -коэффиценттер, бұл коэффиценттер құйынның өшуді , немесе өсуін , білдіреді. Рейнольдстің үлкен шамалары үшін (1. 3) теңдеуі мына түрде болады
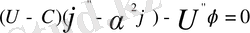 (1. 4)
(1. 4)
Шекаралық қабаттан тыс жерде құйын жоғалады, осыған мына шектік шарттар сәйкес келеді:
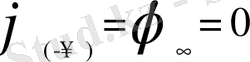
Егер шекаралық қабаттағы жылдамдық сызықтық сипатта болса онда теңдеу мына түрде болады:
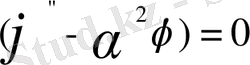
Осындай теңдеудің шешімі мына түрде болады:
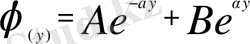
Бұл теңдеу ағынның әртүрлі бөліктерін сипаттайды:
Мұндағы -шекаралық қабаттың қалыңдығы, осы шамаға байланысты Рейнельдс саны анықталады.
Шекаралық аймақтағы жылдамдық компонентерінің теңдігін және көріністердің үздіксіздігін пайдаланып релей мына шешімді алды:
Фазалық жылдамдық тұрақты болып қалады:
шамасы кеңістіктік күшею шамасы деп аталады және ол құйынның күшею шамасын сипаттайды. Толқындық санға қарағанда ол әр түрлі мән қабылдай алады. Максималдық коэффициенті
тең болғанда ол 0, 402 мәнін қабылдайды. Құйынның толқын ұзындығы
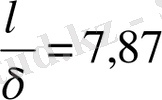 тең. Амплитуданың ең үлкен мәні үшін қалыңдық
үшін
тең. Амплитуданың ең үлкен мәні үшін қалыңдық
үшін
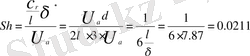
Осыдан шекаралық қабат қалыңдығына байланысты шексіз жиілік 0, 0211 -ге тең екені анықталады. Жүргізілген тәжірибелер нәтижесі теориялық мәндермен сәйкес келеді. Тәжірибелік нәтижелермен анықталған Струхаль саны мына тәуелділікке бағынады
Мұндағы к-тұрақты, ол ағынның ағып өтуінің бастапқы шарттарына байланысты. Re< мәні үшін к саны 0, 0195-ке тең, ал к=0. 0211 үшін Re< мәнін қабылдайды. Мұндай айырмашылықтар қондырғының каналдарының әр түрлі формада болуына байланысты. к коэффициентінің мәні шекаралық қабаттың қалыңдығына және құбырлардан ағып өтетін ағынның жылдамдығына байланысты анықталады:
Құбыр аймағы мен ауысу нүктесіне дейінгі қашықтықтың 85-95%-ы құйынның сызықтық өсу аймағын құрайды, яғни тәжірибе арқылы шекаралық қабаттағы тербеліс жылдамдығын анықтауға болады, ол синусойдалық формаға сәйкес келеді. 1. 3-ші суретте көрсетілген.
§1-2. Құйын өсуінің сызықтық емес теориясы негізінде ауысу құбылысын қарастыру.
Сызықтық теориясы маңызды тәжірибелік нәтижелер береді. Бірақ бұл теория құйынды ағыстың ұзақ уақыт өсуі туралы дұрыс шешімдер бере алмайды.
Рейнельдс саны үшін тұрақсыз ортадағы құйын уақыт бойынша өзгеріп отырады. Бірақ тәжірибе жүзінде олар уақыт бойынша тұрақталады немесе ламинарлық ағыс жойылады. Осыған байланысты сызықтық емес мүшелерді ескеру керек болады.
Осындай есепті шешудің модифицирленген әдісін академик Струминский В. В ұсынған болатын. Бұл әдісте ток функциясы мына түрде болады:
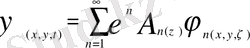 (1. 5)
(1. 5)
Бұл әдісте уақыт үзіндісі мына түрде беріледі:
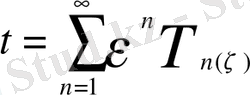 (1. 6)
(1. 6)
Мұндағы -кіші параметр, -белгісіз функциялар жиындығы, - ыдырау коэффициенті, -координата және уақытқа тәуелді функция. Осы шарттарды қолдана отырып қозғалыстың теңдеуіне (1. 5) және (1. 6) қойып рекурренттік дифференциалдық теңдеулер аламыз. Бұл теңдеу кейін жай дифференциалдық теңдеуге айналады. Бірінші жуықтауда құйын қозғалысы үшін ток функциясы мына түрде болады:
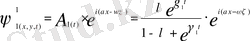
{ тұрақты ағыс бөлігінде t -ның үлкен мәндері үшін бірінші жуықтау нөлге ұмтылады, ал тұрақсыз бөлігінде уақыт бойынша тұрақтанады. Басқа жуықтаулар да осыған ұқсас жүреді.
Егер бастапқы шарттарды өзгертім төмендегі теңдеудің жеке шешімін тапсақ
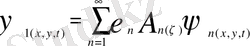
Мынаны аламыз
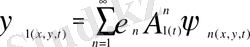 (1. 7)
(1. 7)
Мұндағы -ның мәні бір болады. болғанда және t мәнінің өсуі кезінде ток функциясы нөлге ұмтылады. Ал егер болғанда және t -ның аз мәні үшін (1. 7) -ті жазамыз
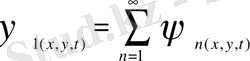
Бұл құйынның уақыт бойынша тұрақтанатынын білдіреді бірақ ағыс ламинарлы және периодты болады.
Осы жұмыстарды негізге ала отырып құйындалған ламинарлық ағыс кейін тағы да ламинарлық ағысқа айналады, бірақ оның құрылымы күрделі болады. Бұл ауысу туралы ең алғаш Л. Д. Ландау ұсынған болатын. Бірақ жаңа перидтық ламинарлық ағыстың құпиялары әлі ашылмады. Бұл күрделі қозғалыс құрылымы реттелген құйындарға байланысты, яғни әрбір жеке құйын ішкі ламинарлық ағыстан құралады. Пайда болған құйын белгілі бір өлшемде болу керек. Бірақ бұл ағыс турбуленттік емес өйткені турбулеттік құйындардың жиілігі ауқымды болу керек. Алғашқы кіші масштабтағы құйындар ағыс бойымен төмен қарай қозғалып басқа қлкен масштаптағы құйындармен бірігуі мүмкін. Пайда болған құйын әлі де ламинарлық сипатта болады.
Қазіргі кезде тұрақтылықтың сызықтық емес теория әлі маңызды практикалық нәтиже бермеді, бірақ болашақта үлкен нәтижелер күтілуде.
Сонымен қатар екінші ретті тұрақсыздықтар теориясын құру көзделді. Бұл теория бойынша үлкен масштабтағы құйындар фонында кіші масштабтағы пульсациялар жылдам өседі. Осыдан Эммонс дақтары пайда болады. Бұл теория 3-4 -ші өзгеру аймақтарын сипаттайды және турбуленттікке ауысу кезіндегі шектік Рейнольдс санын анықтауға мүмкіндік береді.
§1-3. осесимметриялық ағынның бастапқы және соңғы бөліктеріне ағыстың периодтық структурасының әсері.
Шекаралық қабаттағы тұрақсыздықтың нәтижесінде құйын пайда болады. Еркін ағындағы құйындар ағыспен төмен тарала отырып өзінің көлемін үлкейтеді, бір -бірімен әсерлеседі және бұзылады осыдан турбуленттік пайда болады. Осесимметриялық ағыстың бастапқы және соңғы бөліктерін эксперименттік зерттеу кезінде олардың спектральдық және корреляциялық әдістермен белгіленеді. Егер құбырдың шетінде құйындар пайда болып және олардың арақашықтығы құбыр диаметрінен әлде қайда аз болса онда құйындар бірігуі мүмкін. Бұл үлкен масштабтағы құйындардың пайда болуына және шекаралық қабаттың жылдам өсуіне алып келеді. Құйындардың арақашықтығы екі еселеніп соңында құбыр диаметрімен теңеседі. әрбір құйындардың қосылуы олардың тұрақсыздығына алып келеді, процестің соңында олардың тұрақтылығы бұзылады. Осыдан кейін үлкен масштабтағы құйындар таралып, кең көлемді жиіліктегі пульсациялық жылдамдық құрылады.
Рейнельдстің осы мәнінде шекралық қабаттың қалыңдығын өзгертіп ағынның бастапқы бөлігіндегі құйынның пайда болу сипатына әсер етуге болады. Шекаралық қабаттың қалыңдығының өсуі ламинарлық ағыс ауданының өсуіне және үлкен масштабты құйындардың пайда болуына алып келеді, ал керісінше азаюы кіші масштабтағы құйындардың пайда болуына алып келеді. Бұл құйындар бір-бірімен әсерлеседі. Осындай әсерлесулер нәтижесінде ағыстың төменгі бөлігінде белгілі бір жиіліктегі периодтық құйындар пайда болады. Мұндағы жиілік Рейнольдс санына тәуелді болмайды. Ал Струхаль саны шамамен 0, 4-0, 6-ға тең болады.
1. 4 -ші суретте Струхаль санының Рейнольдс санына тәуелділігі және пульсациялық жылдамдық жиілігі көрсетілген. Тәжірибеде шекаралық қабаттың қалыңдығы өту жылдамдығына, құбыр формасына және әртүрлі ұзындықтағы жалғамаларды қолдану әсрінен өзгерді.
Зерттеулер нәтижесінде дискреттік құйын структурасы ағынның акустикалық шудың негізі болып табылады.
Еркін ағынның бастапқы және соңғы бөліктеріндегі құйындық структура құбылысы, сонымен қатар олардың сипттамасына акустикалық әсердің ықплы туралы А. С Геневскийдің, Е. В. Власованың және А. В. Колесинкованың “Аэроакустикалық әсерлер”атты монографиясынан толық білуге болады.
3, 16гц жиіліктегі турбуленттік ағынның спекральдық сипаттамасы өлшенді, соның нәтижесінде бастапқы бөліктерде sh=0, 2-0, 8 шамасында қысымның және пульсациялық жылдамдықтың максимумдарының пайда болуы, өсуі және жоғалуы орын алатыны анықталды, 1. 5-ші сурет. Корреляциялық әдіс те оның периодтық ағыс екенін көрсетеді. Өйткені пульсациялық жылдамдығы және x\d=3-4 болатын құйынның кореляциясының кеңістіктік қисығы толқын тәрізді болып келеді. 1. 6-сурет. Ол бірнеше рет ордината өстерімен қиылысады. Екі нөлдік мәндердің арақашықтығынан құйындардың масштабын анықтауға болады. Жұмыста ағыстың периодтық сипатының көрінуінің сандық мәндері кореляциялық анализді пайдалана отырып алынды. Мұндағы (1. 7-сурет) . Графиктерден Струхаль санының басқа мәндеріне қарағанда ағынның периодтығы Sh=0. 48 мәнінде айқын көрінеді.
кеңістіктік-уақыттық кореляцияны өлшегенде осынған жақын нәтиже берген. ( ) .
Ағыстың периодтық сипаттамасын алу үшін шекаралық қабаттың сыртқы орта әсетіне сезгіштігі ескерілген болатын. Мысалы, \29\жұмыста әртүрлі жиіліктегі акустикалық қозғалысқа турбуленттік құйынның реакциясы зерттелді. Пульсациялық жылдамдықтың орташа квадраттық мәні құбырдың бөлігіндегі интенсивтік пульсацияға байланысты анықталды. Ол ағыс бойымен таралатын дыбыс көзі арқылы эксперимент жүргізуші береді. Ағыс өсіндегі интенсивтік пульсация Струхаль санына және қозу шамасына тәуелді болатыны анықталды. 1. 8-сурет. максималдық мәні Sh=0. 3 -ке сәйкес келеді, ал -ның үлкен мәндері үшін “қанығу”болады, яғни -ның алдағы өсуі -ге айтарлықтай әсер етпейді. Бұл нәтижелерді пайдалана отырып Sh=0. 3 мәнінде ағынның сыртқы дыбыстарға айтпрлықтай сезімтал келетіні анықталды. Осыған ұқсас нәтижелер \37\жұмыста сипатталады. Кейбір жағдайларда Струхаль санының Sh=0. 35-0. 50 мәндері алынған, бұл резервердің әртүрлі ерекшеліктеріне және әртүрлі авторлардың берген шарттарына байланысты деп түсіндіріледі.
Толқынның құрылымын анықтаудың фазалық орталау әдісі туралы айтып кеткен жөн, бұл туралы \38, 39, 40\жұмыстарда сипатталған. Әдістің ерекшелігі керекті гармоникалық сигналды алу үшін синхрондық детекторды пайдалану болып табылады. Бұл әдіске §2. 8 те ерекше назар аударылады.
§1. 4 Еркін ағыстың сипатына сыртқы акустикалық әсердің ықпалы.
Ағынның дыбысқа деген сезгіштігі жүз жыл бұрын анықталған. Бұл құбылысы Релей шекаралық қабаттың тұрақсыздығы тұрғысынан түсіндірген болатын. Бірақ ағынның құрылымына дыбыстың әсеріне байланысты негізгі зерттеулер соңғы жылдарда жүргізілуде. Турбуленттік ағын шудың негізгі көзі болып табылады. Осыған байланысты егер күшті акустикалық өрісті салса ағынның турбуленттікке табиғи ауысуы және оның негізгі сипаты бұзылады.
Осы бағыттағы тәжірибелік жұмыстарды Е. В. Власов және А. С. Гиневский\41, 42, 43\ жүргізген болатын, сонымен қатар С. И. Исатаев және С. Б. Тарасов да \31, 44\зерттеген. Диаметрі 10 55мм болатын құбырдан ағып өтетін изотермиялық турбуленттік ағын зерттелді. Ағынның жылдамдығы 10 114м\с диапазонында болды. Акустикалық өріс бір немесе үш динамиктердің көмегімен жасалды. Ол ағыс бойына немесе оған көлденең бағытта орналастырылды. Дыбыстық қысым L шамасы 120-125дб болды. Рейнельдс санының диапазонында құбыр қимасындағы(ағын центрінде) бастапқы турбулкенттік 1% құрайды. x\d=8 шамасындағы датчик әсердің жиілігіне тәуелді орташа және бойлық пульсацмялық жылдамдықты белгілеп отырды. Датчик ағын өсінің бойында орналасқан.
Струхаль санының Sh=0. 2 1 диапазонындағы ықпал орташа жылдамдықтың азаюына және пульсацияның өсуіне алып келетіні анықталды. Сонымен қатар ең үлкен эффект Sh=0. 3 0. 6 диапазонында байқалды. Sh=1 5 және
Re болғанда әсер кері сипатта болады, яғни орташа жылдамдық өсіп, ал пульсация кемиді. Бұл эффекттердің шамасы дыбыстық қысымның дәрижесіне және Рейнельдс санына тәуелді. Егер құбыр жиігіндегі шекаралық қабат ламинарлы болса және дыбыстық өріс ағыс бойымен бағытталса, онда көрсетілген эффекттер өте аз дыбыстық қысымда L=90 100дб бақалады. 1, 9-сурет.
1, 10-суретте Струхаль санының екі мәніне байланысты алынған орташа және пульсациялық жылдамдықтар көрсетілген. Суреттен акустикалық әсердің ағын құрылымына деген ықпалы екі жақты сипатта болатыны көрінеді. Струхаль санының аз мәнінде (Sh=0. 4) орташа жылдамдық тез төмендейді, яғни турбуленттік ауысу қарқындалады. Пульсациялық жасаушының азаюы және турбуленттік ауысудың әлсіреуі салдарынан жоғары қарқынды әсер керісінше бастапқы бөліктің созылуына, ағынның ұзақ болуына және орташа жылдамдықтың жәймен төмендеуіне алып келеді. Орташа жылдамдықтың көлденең көрінісін өлшегенде де осындай нәтиже алынған. Акустикалық әсердің екі жақты сипаты туралы \36, 45-49\жұмыстарында көрсетілген. Бұл жұмыстарда жазық, осесимметриялық ағынды және ауыспалы тығыздықты ағын зерттелген.
Егер акустикалық сигнал жазық толқын ретінде таралса онда дыбыстық толқында пульсациялық қысым мен жылдамдықтың байланысы мына түрде болады:
Ағындағы пульсациялық қысымның аэродинамикалық табиғатын изотроптық турбуленттегі пульсациялық қысым сияқты сипаттауға болады
Енгізілген пульсациялық қысым бастапқы турбуленттік пульсациялық қысымға пропорционал болса әсер эффектісі айқын көріне бастайды, немесе
Мұндағы -тәжірибелік коэффициент. мәніне ағын өсіндегі максималды пульсация мәнін қабылдауға болады Ал енгізілген пульсацияға \42\мәнін қойсақ болады. , , M мәндерін қойып мына шаманы аламыз , онда болады. Қозу жоқ кездегі ағын өсіндегі максималдық қысымы мен енгізілген өріс қысымы бір ретте орналасса акустикалық әсер ағысқа айтарлықтай үлкен әсер тигізеді. Сондықтан ағын құрылымына айтарлықтай әсер ету үшін жылдамдықтың өсуіне байланысты дыбыстық қысымды L да өсіру керек. \35\жұмысқа байланысты :
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz