Комплекс сандар. Комплекс айналымы

1 лекция

Комплекс сандар

1. Лекция мақсаты.

Студенттерді комплекс сандар ұғымымен, оның геометриялық мағынасымен және шығу жағдайымен таныстыру

2. Түйін сөздер.

Комплекс санның модулі, аргументі.

3. Лекцияның қысқаша мазмұны.

Келесі түрдегі өрнекті z = x+iy (I) комплекс сан дейміз. Бұл комплекс санның алгебралық түрі. Мұнда i = $\ \sqrt{- i}$ комплекс санның нақты бөлігін x = Rez деп, жорамал бөлігін 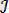mz = y белгілейміз. $\widetilde{z\ }$ = x+iy комплекс санын, z = x+iy санына түйіндес сан дейді.

z = x+iy комплекс санына XOY жазықтығына нүкте болып өрнектеледі.

y

M

s

φ . y

0 x x

S = $\widetilde{OM}$ z комплекс санының модулі S = $\sqrt{x^{2} + y^{2}}$ ал φ = Arg z комплекс санның аргументі длеп аталады.

Arg z = arg z + 2kπ (k=0; ±1, ±2…)

Алгебралық түрдегі комплекс сандарға амалдар.

1. Z1= x1+iy1, z2= x2+iy2комплекс сандар қосындысы (айырымы) - комплекс сан болады және келесі түрде анықталады. z1± z2= (x1±x2) + i (y1±y2)
2. z1, z2комплекс сандар көбейтіндісі комплекс сан болады және келесі түрде анықталады, z1. z2= (x1x2-y1y2) + (x1y2 +x2y1) комплекс сандар қатынасы:
3. z1, z2комплекс сандар қатынасы

$$\frac{z_{1}}{z_{2}} = \frac{x_{1}x_{2} + y_{1}y_{2}}{x_{2}^{2} + y_{2}^{2}} + i\frac{x_{2}y_{1} - x_{1}y_{2}}{x_{2}^{2}{+ y}_{2}^{2}}$$

Комплекс санның тригонометриялық түрі және оларға амалдар.

Алгебралық түрдегі комплекс z = x+iy сан тригонометриялық түрге келтіреді. Жоғарыдағы суреттен x= $\int_{}^{}{\cos\varphi}$ y= $\int_{}^{}{\sin\varphi}$

сонда, z =S (cosφ + sinφ) (2)

келесі комплекс сандарды қарастырайық,

z ₁ =S ₁ (cosφ ₁ + sinφ ₁ ) S ₁ = $Z1$ , Arg z ₁ = φ ₁

z ₂ =S ₂ (cosφ ₂ + sinφ ₂ ) S ₂ = $Z1$ , Arg z ₂ = φ ₂

Сонда,

z ₁ $\ \times$ z ₂ = S ₁ $\ \times$ S ₂ $\left. ⟦\cos(\varphi 1 + \varphi 2) + \ isin\ (\varphi 1 + \varphi 2) \right. ⟧$

$Z1 \times Z2$ = $Z1 \times Z2$ Arg ( $Z1 \times Z2$ ) =Arg z ₁ -Arg z ₂

Екі комплекс санның қатынасы келесі формуламен анықталады;

$$\frac{z_{1}}{z_{2}} = \frac{S_{1}}{S_{2}}\left\lbrack \cos\left( \varphi_{1} - \varphi_{2} \right) + i\sin\left( \varphi_{1} - \varphi_{2} \right) \right\rbrack$$

$\left \frac{z_{1}}{z_{2}} \right = \frac{\left z_{1} \right}{\left z_{1} \right}$ , Arg $\frac{Z1}{Z2}$ = Arg z ₁ -Arg z ₂

4. Бақылау сұрақтары.

1. Комплекс сандардың аргументі, модулі деген не?
2. Комплекс сандардың геометриялық мағынасы не болады?
3. Комплекс сандардың қосындысы, айырымы, қатынасы қандай сан болады?
4. Комплекс санның тригонометриялық түрін жаз және оларға қандай амалдар қолдануға болады?
5. Пайдаланылған әдебиеттер(оқу құралдары)

1. Привалов И. И. Введение в теорию функций комплексного переменного. Изд. «Наука» М. 1977 г.
2. Лаврентьев М. А. Методы теории функций комплексного переменного. Изд. «Наука» М. 1987 г.
3. Смирнов В. И. Курс высшей математики том 3, часть вторая. Изд. «Наука»
4. Тихонов. А. Н. Свешников А. Г. Теория функций комплексной переменной Изд. «Наука» М. 1974г.
5. Краснов М. Л. Киселев А. И. Макаренко Г. И. Функций комплексного переменного, Операционное исчисление, Теория устойчивости.
6. Волковоский Л. И. Лунц Г. Л. Араманович И. Г. Зборник задач по теорий функций комплексного переменного. Изд. «Наука».
7. Привалов И. И. Комплекс айнымалы функция теориясына кіріспе. 1969 жыл.

2 лекция

Комплекс айналымы.

Функциялар.

1. Лекция мақсаты.

Студенттерді комплекс айналымы, функция ұғымы мен және оның екі аймақ арасындағы бейнелеу екендігін түсіндіру

2. Түйін сөздер.

Бейне, түпбейне, жиынның ішкі нүктесі, тұйық жиын.

3. Лекцияның қысқаша мазмұны.

Комплекс сандардан құралған Е жиынын қарастырайық. z = x+iy комплекс саны Е жиынының әрбір нүктесіне сәйкес келсін. Бұл жағдайда, z - айнымалы, ал Е-ні оның өзгеру аймағы дейміз.

Анықтама.

Егер Е аймағында өзгеретін комплекс айнымалы z - тің әрбір мәніне қандайда бір заңдылықпен Q аймағының W= U (x, y) +iv(x, y) айнымалының бір мәніне сәйкес келсе, онда айнымалы W-ні, айнымалы Z- тің функциясы дейді және оны былай белгілейді

W= f (z), немесе W= φ (z), (1)

Тәуелсіз айнымалы W- нің қабылдайтын барлық мәәндерінің жиынын Q деп белгілесек, онда комплекс Z жазықтығында жатқан Е айнымалының әрбәр нүктесіне, комплекс W жазықтығында жатқан Q аймағының белгілі бір нүктесі сәйкес келеді.

y V

Q

. z E W=f(z) W

O X O X

Былайша айтқанда, W= f (z) функциясы Е аймағын Q аймағына түрлендіреді немесе бейнелейді.

f (z) функциясының Е жиынынан қабылдайтын мәндерін, W= f (z) бейнелеуі бойынша, Е жиынының бейнесі дейді, және f (z) деп белгілейді, ал Е жиынын f (z) -тің түп бейнесі дейді. Егер Q аймағының әрбір нүктесіне Е аймағының бір немесе бірнеше нүктесі сәйкес келсе, онда айнымалы Z- ті айнымалы W-нің функциясы дейді және келесі түрде белгілейді

Z = φ (w), (2)

(2) функцияны (1) функцияның кері функяиясы дейді.

Егер центрі Р нүктесіндегі жеткілікті кішкене R дөңгелектің барлық нүктелері Е жиынының ішкі нүктесі дейді.

Е жиынын (область) дейміз, егер келесі екі шарт орындалса:

1. Е жиынының әрбір нүктесі оның ішкі нүктесі болса;
2. Жиынның кезкелген екі нүктесін, сол жиынның ішінде жатқан сынық сыызықтармен қосуға болса;

Аймақ Е берілсе, жазықтықтың бүкіл нүктелерін осы Е аймағына қатысты екі класқа бөлуге болады. Бірінші класқа Е аймағының барлық нүктелерін жатқызамыз, ал екінші класқа Е аймағына жатпайтын нүктелерді енгіземіз. Е аймағында жатпайтын нүкте Q екі типті болуы мүмкін, не центірі осы Q нүктесіндегі жеткілікті кішкене дөңгелектің барлық барлық нүктелері Е аймағында жатпайды, онда Q нүктесін Е аймағының сыртқы нүктесі деп атаймыз, не центрі Q нүктесіндегі мейлінші кішкене дөңгелекте Е жиынының нүктелері де жатады, онда Q нүктесін Е аймағының шекаралық нүктесі деп атайды. Е аймағының барлық шекоралық нүктесінің жиынын осыаймақтың шекарасы дейміз. Е аймағы мен оның шекарасынан тұратын жиын тұйық жиын деп аталады және келесі түрде белгіленеді Е.

4. Бақылау сұрақтары.

1. Комплекс айнымалы функция анықтамасы.
2. Бейне және түпбейне дегеніміз не?
3. Аймақ дегеніміз не және тұйықталған жиын анықтамасы.
4. Бір байланысты және көпбайланысты аймақ.

1. Z нүктесінен Е аймағының сыртқы нүктесі дейміз, егер оның аз Е аймағының Е аймағына кірмейтңн болса
2. Z нүктесін Е аймағына шегараның нүктесің дейміз, егер оның аз Е аймағында Е жиынының нүктелерімен оған (Е жиыны) кірмейтін нүктелер де болса.
3. Жиынға оның барлық шекараларының нүктелерін қоссақ, одан шыққан жиынды тұнықталған дейміз.
4. f(z) функцияларын Е аймағында бірпарақ функция дейміз, егер z - тің әрбір мәніне функцияның әрбір мәні сәйкес келсе.

Үздіксіздігі.

Анықтама.

Е жиынында анықталған f(z) функциясын, z ₀ Є Е нүктесінде үздіксіз дейміз, егер функцияның z ₀ нүктесінде шекті мәні болға, ал ақырғы және f(z ₀ ) тең болса, онда f(z) - z ₀ нүтесінде үздіксіз дейміз.

$\lim_{\begin{array}{r} z \rightarrow z0 \\ \end{array}}$ f (z) = f(z ₀ )

3 лекция

Шек және функцияның үздіксіздігі.

Комплекс айнымалы қарапайым функциялар.

1. Лекция мақсаты.

Студенттерді комплекс айналымы функцияларының шек және үздіксіздігімен таныстыру.

2. Түйін сөздер.

Шек, үздіксіздік.

3. Лекцияның қысқаша мазмұны.

W= f (z) функциясы z ₀ = x ₀ +iy ₀ нүктесінің аймағында анықталған және бірмәнді болсын.

1. f (z) функциясының z→ z0шегі болады дейміз, егер

$\lim_{\begin{array}{r} x \rightarrow x_{0} \\ y \rightarrow y_{0} \end{array}}$ u (x, y) = u (x _0, y ₀ ) $\lim_{\begin{array}{r} x \rightarrow x_{0} \\ y \rightarrow y_{0} \end{array}}$ v (x, y) = v (x _0, y ₀ )

Шектері бар болса, былайша айтқанда

$\lim_{\begin{array}{r} z \rightarrow z_{0} \\ \end{array}}$ f (z) =u ₀ +iv ₀ = w ₀ (1)

Нақты айнымалы функциялар шектерінің комплекс айнымалы функциялар шегіне де көшеді.

$\lim$ (f±g ) = $\lim$ f ± $\lim$ g, $\lim$ (f, g ) = $\lim$ f × $\lim$ g

$\lim$ $\frac{f}{g}$ = $\frac{lim\ f\ }{lim\ g\ }$ (егер $\lim \neq 0$ )

2. f (z) функциясын z0нүктесінде үздіксіз дейміз, егер ол (f (z) ) z0нүктесінің аймағында (және z0нүктесінде) анықталып және келесі шек болса,

$\lim_{\begin{array}{r} z \rightarrow z_{0} \\ \end{array}}$ f (z) = f (z ₀ )

Енді комплекс айнымалы қарапайым функцияларға тоқталайық.

e ^z , sinz, cosz комплекс функциялары, жинақты дәрежелі қатардың қосындысы ретінде анықталады.

e ^z = 1+ $\frac{z}{11}\$ + $\frac{z2}{\ 21}$ +….

sinz = z - $\frac{z3}{31}$ + $\frac{z5}{51}$ - $\frac{z7}{71}$ +…. . (3)

cosz = 1- $\frac{z2}{21}$ + $\frac{z4}{41}$ - $\frac{z6}{61}$ +…. .

e ^z қасиеттері 1) e ^z1+z2 = e ^z1 e ^z2 , мұндағы z ₁ , z ₂ кезкелген комплекс сандар. 2) e ^z+2πi _{= e} ^z (k=0, ±1, ± 2 …) $e^{z}$ функциясының период 2πi-ге тең. $e^{z}, \sin z, \cos z$ функциялары үшін Эйлер орындалады орындалады.

e ^iz = cosz+ i sinz, e- ^iz = cosz - i sinz, (4)

Бұдан, cosz= $\frac{e^{iz} + e^{- iz}}{2};$ $\sin z = \frac{e^{iz} - e^{- iz}}{2_{i}}$ (5)

Егер $z = x + iy,$ $e^{z} = e^{x + iy} = e^{x}*e^{iy}$

$e^{z} = e^{x}\left( \cos y + {isin}y \right)$

tgz, ctgz, келесі формулалармен анықталады

$\tan z = \frac{\sin z}{\cos z}, \ \ \ \cot z = \frac{\cos z}{\sin z}$ (6)

Тригонометрияның барлық формулалары, комплекс айнымалы тригонометриялық функциялар үшін де орындалады.

shz, chz, thz, cthz гиперболалық функциялар келесі формулалармен анықталады.

shz= $\frac{e^{z} - e^{- z}}{2};$ ${sh}z = \frac{e^{z} + e^{- z}}{2_{}}$

${th}z = \frac{{sh}z}{{ch}z}, \ \ \ {cth}z = \frac{{ch}z}{{sh}_{z}}$

Тригонометрияның жеңе гиперболалық функциялар келесі формулалармен байланысады

sinz = -ishiz shz = -ishiz

cosz = chiz chz = chiz

tgz = -ithiz thz = -itgiz

ctgz = ticthiz cthz = ctgiz

Логарифм Ln z (z≠0) функциясы, көрсеткіштік функцияға кері функция ретінде анықталады.

$lnz = lnz$ + iArgz = $\ln$ $z$ + iargz + kπi (k=0, $\pm 1, \ \pm 2\ldots$ )

Ln z көпмәнді функция. Ln z функциясының К=0 мәніне сәйкес мәнін оның бас мәні дейді, және келесі түрде белгілейді Ln z

$lnz = lnz + \ iargz$

Arcsinz, Arccosz, Arctgz, Arcctgz функциялары, sinw, cosw, tgw, ctgw функцияларына кері функциялар ретінде анықталады. Мысалы z= sinw, бұдан w= Arcsinz. Бұл функциялан көпмәнді, олар логарифмдік функциялар арқылы келесі формулалармен өрнектеледі

$ark\sin z = - i\ln{(iz + \sqrt{1 - z^{2}\ \ \ ) }}$ (9)

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ark\cos z = - i\ln{(z + \sqrt{z^{2} - 1\ \ \ ) }}$ (10)

$ark{tg}z = - \frac{i}{2}\ln{(\frac{1 + iz}{1 - iz}}$ ) (11)

$arkc{tg}z = - \frac{i}{2}\ln{(\frac{z + i}{z - i}) }$ (12)

Бақылау сұрақтар

1. Комплекс айнымалы функция шегінің анықтамасы.
2. Комплекс айнымалы функция үздіксіздігі.
3. Тұйықталған аймақта үздіксіз және шектелген комплекс айнымалы функциялар үшін, нақты функциялар қасиеттері орындалама?
4. Комплекс айнымалы қарапайым функциялар формулаларын жаттаңдар.

Пайдаланған оқулықтар

1. Лаврентьев М. А. Шабат Б. В. Методы теории функций комплексного переменного Изд. «Наука» М. 1987 г.
2. Тихонов А. Н. Свешников А. Г. Теория функций комплексной переменной Изд. «Наука» М. 1974 г.
3. Краснов М. Л. Киселов А. И. Функций комплексного переменного.
4. Волковский Л. И и д. р Сборник задач по теории функции комплексного переменного Изд. «Наука»

4 лекция

Комплекс айнымалы функцияларды дифференциалдау.

Коши-Риман шарты. Аналитикалық функциялар.

1. Лекция мақсаты.

Студенттерді комплекс айналымы функцияларының туындысымен және аналитикалық функцияға ұғымымен таныстыру.

2. Түйін сөздер.

Коши-Риман шарты. Аналитикалық функциялар. Конформды бейнелеу.

3. Лекцияның қысқаша мазмұны.

W= f (z) функциясы комплекс айнымалы z-тің жазықтығындағы Е аймағында анықталған бір мәнді функция болсын. Комплекс айнымалы бойынша дифференциалдау анықтамасы формальді жағынан нақты айнымалы функциялар үшін берілген анықтамамен бірдей

$z + \mathrm{\Delta}z, \ \ \ \ \ \ \ w + \mathrm{\Delta}w, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathrm{\Delta}w = f(z + \mathrm{\Delta}z) - f(z)$

$$\lim_{\mathrm{\Delta}z \rightarrow 0}{\frac{\mathrm{\Delta}w}{\mathrm{\Delta}z}^{} =}\lim_{\mathrm{\Delta}z \rightarrow 0}\frac{f(z + \mathrm{\Delta}z) - f(z) }{\mathrm{\Delta}z} = f^{I}(Z)$$

$$z \neq x + iy, \ \ \ z + \mathrm{\Delta}z = (x + \mathrm{\Delta}x) + i(y + \mathrm{\Delta}y) \ \ \ \ \mathrm{\Delta}z = \mathrm{\Delta}x + i\mathrm{\Delta}y$$

$$f^{I}(z) = \lim_{\mathrm{\Delta}z \rightarrow 0}{\frac{\mathrm{\Delta}w}{\mathrm{\Delta}z} = \lim_{\begin{array}{r} x \rightarrow x_{0} \\ y \rightarrow y_{0} \end{array}}}\underset{}{\frac{\left\lbrack u(x + \mathrm{\Delta}x\lambda y + \mathrm{\Delta}y) - u(x, y) \right\rbrack + i\left\lbrack v(x + \mathrm{\Delta}x\lambda y + \mathrm{\Delta}y) - v(x, y) \right\rbrack}{\mathrm{\Delta}x + i\mathrm{\Delta}y}}$$

$$\mathrm{\Delta}y = 0, \ \mathrm{\Delta}x \rightarrow 0\ деп\ алайың, \ онда$$

$$f^{I}(z) = \lim_{\mathrm{\Delta}x \rightarrow 0}\left\lbrack \frac{u(x + \mathrm{\Delta}x, y) - u(x, y) }{\mathrm{\Delta}x} + i\frac{v(x\mathrm{\Delta}x, y) - v(x, y) }{\mathrm{\Delta}x} \right\rbrack = \frac{\delta u}{\delta x} + i\frac{\delta v}{\delta x}$$

$$f^{I}(z) = \lim_{\begin{array}{r} \mathrm{\Delta}y \rightarrow 0 \\ \mathrm{\Delta}x = 0 \end{array}}\left\lbrack \frac{u(x, y + \mathrm{\Delta}y) - u(x, y) }{i\mathrm{\Delta}y} + i\frac{v(x < y + \mathrm{\Delta}y) - v(x, y) }{i\mathrm{\Delta}y} \right\rbrack = \frac{\delta v}{\delta y} + i\frac{\delta u}{\delta y}$$

1. Және (2) өрнектердің сол жақтары тең, олай болса

$\frac{\delta u}{\delta x} = \frac{\delta v}{\delta y}, \ \ \ \frac{\delta v}{\delta x} = - \frac{\delta u}{\delta y}\ \$ (3)

(3) Теңдеу Коши-Риман шарты деп аталады. Коши-Риман шартын ескеріп, f (z) функциясының туындысын келесі түрде жазамыз.

$f^{I}(z) = \frac{\delta u}{\delta x} + \ i\frac{\delta v}{\delta x} = \frac{\delta v}{\delta y} - i\frac{\delta u}{\delta y} = \frac{\delta u}{\delta x} - i\frac{\delta u}{\delta y} = \frac{\delta v}{\delta y} + i\frac{\delta v}{\delta x}$ (4)

Егер f (z) функциясы Е аймағын барлық нүктелерінде дифференциялданса, ал оның туындысы бұл аймақта үздіксіз болса, онда f (z) функциясын Е аймағында аналитикалық функция дейді. Е аймағында W= U (x, y) +iv(x, y) функциясының Коши-Риман шартын қанағаттандыратын үздіксіз дербес туындысының болуы, f (z) функциясының Е аймағында аналитикалық функция болуының қажетті және жеткілікті шарты болады.

Конформды бейнелеу ұғымы.

... жалғасы

Комплекс айнымалы жалпы дәрежелік функция

Операциялық есептеуді дифференциалдық теңдеулерді шешуге қолдану

КОМПЛЕКС САНДАР МЕН ОЛАРҒА ҚОЛДАНЫЛАТЫН АМАЛДАР

Математиканың дамуы барысында комплекс

Комплекс сандар

Комплекс сандарды оқытуға арналған компьтерлік бағдарламаларды қолдану тәсілдері

Комплекс санның модулі

Комплекс саннан түбір табу

Элементарлық алгебрада қолданылуы

Комплекс сандар ұғымы

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс