Дискретті математика: 1-ші лекция - Жиындар, операциялар және функциялар негіздері


1-ші лекция. 3. 02. 03
“Дискретті математика”
Ақпаратты технология және компьютерлерге байланысты салаларында көптеп қолданылады.
Пән ұғымдарын баяндау оқу барысында қолданылатын белгілер:
⮀ - анықтама бойынша белгілейміз,
положим по опред, обозначим, имеет вид;
⇔ - сонда тек сонда (тогда и только тогда) параметрлер эквиваленті;
⇒ - егер . . . (А болса) онда . . . (В болады) (если . . . то . . . )
∀ - кез-келген (для любого), барлық, әрбір сөздерінің орнына қолданылады;
∃ - (существует) бар болады, табылады, ең болмағанда;
⋀, & - коньюнкция - және сөзінің орнына қолданылады;
⋁ (. ) - дезьюнкция - немесе сөзінің орнына қолданылады;
∀ Х Р(х) - әрбір х үшін Р(х) қасиеті орындалады;
∃ Х Р(х) - ең болмағанда бір х үшін Р(х) қасиеті орындалады;
∀ Р(х) әрбір х үшін Р(х) қасиеті орындалады.
1-ші тарау
Жиындар теориясының элементтері
1. 1 Жиындар және олармен операциялар
Жиындар ұғымы - негізгі математикалық терминдердің бірі болып саналады. Жиынның нақтылы анықтамасы жоқ. Жиынды ортақ бір белгі бойынша біріккен объектілердің жиынтығы деуге болады. Мысалы натурал сандар жиыны, түзудің бойындағы нүктелер жиынтығы, нақты коеффициент бар көпмүшеліктер жиыны, кітап беттерінің жиынтығы (5), натурал сандар жиыны, -1, 2, 3, . . . сандар жиыны . . . -4, -3, -2, -1, 0, 1, 2, . . . нақты сандар жиыны, кітап бетіндегі түрді символдар жиыны, студенттер тобы, компьютерлерді жинау кезіндегі орындалатын операциялар жиыны, “Элегант” фирмасының қызметкерлер жиыны т. б. мысалдарды көптеп келтіруге болады.
Егер х объектісі М жиынының элементі болса, онда х М -ге жатады делінеді және х∋М болып белгіленеді. Әдетте жиын латын алфавитінің бас әріптерімен, ал оның элементтері кіші әріптерімен белгіленеді.
Жиындардың өрнектелуі (берілді)
Жиындарды өрнектеу үшін оған қандай элементтердің жататындығын көрсету керек. Оны бірнеше әдістермен жасауға болады.
1. Жиынға жататын элементтер тізімін көрсету арқылы. Тізім фигуралары жақшамен қоршалады.
M:={a 1 , a 2 , …, a k };
2. Жиын элементтерінің (сипаттамалық предикат арқылы немесе) қандай да бір қасиетін көрсету арқылы. Айталық Р(х) А жиынының элементтері қанағаттанатын я қанағаттанбайтын қасиет болсын. Олай болса А жиынының Р ны қанағаттандыратын барлық элементтерінен тұратын М жиынын
М={x} қасиетін қанағат
M={xP(x) } болып жазылады.
3. Туындайтын процедура арқылы:
M={xx:=f}
Ескерту:
Сипаттамалық предикат Р(х) - логикалық тұжырым формасындағы шарт (немесе логикалық мән қайтаратын процедура) . Егер элемент үшін шарт орындалса элемент жиынға жатады, әйтпесе жатпайды.
Туындайтын процедура іске қосылған кезде жиынның элементі болатын объектілер туындайтын процедура.
Мысалдар
- Араб цифрларының жиыны:
M={1, 2, 3, 4, …, 9} немесе M={xx - араб цифрлары}
- Тақ сандар жиыны:
K= {xx=2k+1, k∈Z} немесе K={±1, ±3, ±5, …}
- D={xx - апта күндері немесе D={күй, c…ж}
- P={xx - жай сандар} немесе P={2, 3, 5, 7, 9, 11, …}
Анықтама Егер А барлық элементтері В жиынында жатса, онда А В жиынының ішкі жиыны деп аталады да, А⊆В болып белгіленеді. (А⊄В - А В-ның ішкі жиыны емес)
Бұдан шығатын тұжырым:
А⊆В⇔∀ х (x∈A⇒x∈B), яғни кез-келген х үшін, егер х∈А, онда х∈В. Егер А⊆В болса, онда А жиыны В жиынына кіреді дейміз.
Анықтама А мен В жиындары тең болады, егер А⊆В және В⊆А болса, яғни тең жиындар бірдей элементтерден құралады. (А⊆В&В⊆В) А, В жиындары бір бірінің ішкі жиыны.
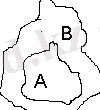
Анықтама Егер А⊆В және В⊆А болса, онда А жиыны В-ға қатаң кіреді дейміз және А В-ның меншікті ішкі жиыны деп аталады.
∀Х Х⊆Х деуге болады. Анықтама бойынша ∀М∅⊂М Егер Х⊆У, ал У⊆Z онда Х⊆Z;
Элементтің жиынға жатуы (∈) мен жиынның басқа жиынның ішкі жиын болуын (⊆), яғни жиынның басқа жиынға кіруі ұғымдарын шатастырмау керек. (∈, ⊆)
О∈{о} және {o}={{o}} болғанымен O∈{{o}} деу дұрыс емес, себебі {{o}} жиынның жалғыз ғана элементі {o} бар. (о - элементі бола алмайды) .
Анықтама Элементтердің ақырлы санынан тұратын жиын, ақырлы жиын деп аталады, керісінше болса ақырсыз жиын деп аталады. Мысалы N, R жиындары ақырсыз. Ақырлы жиындардағы элементтердің саны жиынның қуаты деп аталады және белгілерімен қоршалып жазылады. Мысалы, М - ақырлы жиын болса, оның қуаты M.
Қуаты 0-ге тең жиын, яғни элементтері жоқ жиын бос жиын деп аталады және ∅ белгіленеді ∅=0. ({∅}=1емес)
Бос жиын кез-келген жиынның ішкі жиыны болады деп есептеледі.
Егер А және В жиындары тең болса, олар теңқуатты жиындар деп аталады.
Мысалдар:
- А={1, 2, 3}, B={3, 4, 5} A≠B
- A={1, 2, 3, 4}; B={4, 3, 1, 2}; A=B себебі A⊂B, B⊂A;
- A={1, 2, 3}; B={2, 4, 6}; C={1, 2, 3, 4, 5} A⊂C; B⊄A;
- Мысал M1={xSinx=1}
M 2 ={xx=π/2=2kπ6 x∈Z}
Жиындардың тең екендігін ( M 1 =M 2 ) дәлелдеу керек. Егер х∈М 1 болса, онда x=π/2+2kπ, k∈Z (Sinx=1 теңдеуінің шешімі болған) деуге болады. Демек х∈М 2 . Олай болса М 1 ⊆М 2 .
Егер х∈М 2 болса, яғни х=π/2+2kπ, k∈Z деуге болады, яғни Sinx=1 теңдеуінің шешімі. Демек M 2 ⊆M 1 бұдан M 1 =M 2 .
Анықтама А жиынының барлық ішкі жиындарының жиынтығы оны булсаны немесе дәрежелі жиын деп аталады және Р(А) болып белгілінеді (2 А болып та белгіленеді) .
Сонымен,
2 А =P(A) ⇆{BB⊆A} немесе 2 А
Мысалдар:
Егер А={1, 2, 3} P(A) ={∅, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 2, 3}}
Әдетте нақтылы талдауларда барлық жиындардың элементтері, әр жағдай үшін қажетті дәрежедегікең U жиынымен алынады. Ол универсум деп аталады немесе универсал жиын.
Анықтама Қарастыруға болатын барлық мүмкін элементтерден тұратын жиын универсал немесе универсум деп аталады және U болып белгіленеді.
Жиындармен операциялар (амалдар)
P(U) булсанындағы операцияларды қарастырамыз.
- Егер A, B∈P(U) онда, осы А, В жиындарының екеуіне де жататын элементтерден тұратын жиынды А, В жиындарының қиылысуы деп атайды және төмендегідей өрнектеледі
A∩B⇆{xx∈A &(және) x∈B}
{xx∈A&x∈B}
A={1, 2, 3, 4}
B={4, 3, 6, 7}
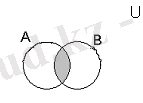 A∩B
A∩B
- A∪B⇆{xx∈A∨(немесе) x∈B}
А, В жиындарының бірігуі деп А, В жиындарының ең болмаса біреуіне жататын элементтерден тұратын жиынды айтады.
A∪B={1, 2, 3, 4, 6, 7}
A∪B
А, В жиындарының қиылысуын олардың көбейтіндісі (А*В), ал бірігуін олардың қосындсы (А+В) деп те атайды.
- А, В жиындарының айырымы деп А\В⇆A-B⇆{xx∈A және х∉В}
А жиынының тек В-ға кірмейтін элементтерінен тұратын жиынды айтамыз
A\B={1, 2}
B\A={6, 7}
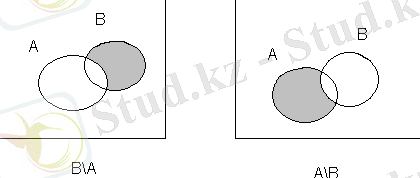
- AB⇆(A\B) ∪(B\A) жиыны. А, В жиындарының сақиналы қосындысы немесе симметриялық айырымы деп аталады.
(А\В) ≠(В\А) А⊕В={1, 2, 6, 7}
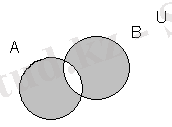
A⊕B
- Ā⇆U\A U универсумындағы А жиынының толықтауышы деп аталады (А-ны U-ға дейін толықтыратын) .
{∩, ∪, −} операциялары бульдік операциялары деп аталады.
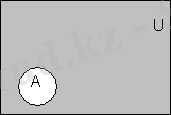
Ā
Анықтама жиындардың геометриялық кескінделуі Эйлер-Вейн диаграммалары деп аталады.
1. Мысалдар. A{1, 2, 3} B{3, 4, 5} болса
A∪B={1, 2, 3, 4, 5}; A∩B={3}; A\B={1, 2}; A⊕B={1, 2, 4, 5}
B\A\{4, 5};
Ā={4, 5};
={1, 2}
Новиков А={1, 2, 3, 4} \ B={3, 4, 6, 7}
2. Симметр. разн А∆В=(A∪B) \(A∩B) ={x(x∈A&x⊄B) ∨(x∉A&x∈B) }
x∈A\B x∈B\A
A⊕B={1, 2, 3, 4, 6, 7}\{3, 4}={1, 2, 6, 7}
Симметриялық айырымның тағы бір формуласы
- A⊕B=A-B=A⊕B⇌(A∪B) \(A∩B)
Біріктіру, Қиылысу операцияларын кез-келгенжиындардың жиыны А i (мұндағы і І жиынының элементтерін қабылдайды) ге де анықтауға болады:
Айталық І - элементтері индекс ретінде қолданылатын қандай да бір жиын болсын және ∀І∈І үшін А і белгілі болсын.
Олай болса,
 ={x∀I∈I x∈A
i
}
={x∀I∈I x∈A
i
}
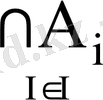 ={x∀I∈I x∈A
i
}
={x∀I∈I x∈A
i
}
Егер I={1, 2, …, n} болса
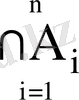 =A
1
∩A
2
∩A
3
…∩A
n
және A
1
∩A
2
∩A
3
…∩A
n
=
=A
1
∩A
2
∩A
3
…∩A
n
және A
1
∩A
2
∩A
3
…∩A
n
=
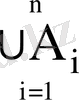
Бөліктеу және бүркеу
Айталық,
{A i i∈I} А жиынының бос емес ішкі жиындары болсын. A i ⊂A
Анықтама
Егер
 =A болса, онда {A
i
i∈I} - (ішкі жиындардың жиыны) А жиынының бүркеуі деп аталады, яғни А жиынының әр элементі А
і
жиындарының ең болмаса біреуіне кірсе
=A болса, онда {A
i
i∈I} - (ішкі жиындардың жиыны) А жиынының бүркеуі деп аталады, яғни А жиынының әр элементі А
і
жиындарының ең болмаса біреуіне кірсе
 А-ның бүркеуі деп аталады.
А-ның бүркеуі деп аталады.
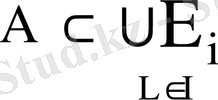

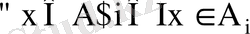
Егер
 жиынының (бүркеудің) элементтері өзара қиылыспаса, яғни А-ның әр элементі А
і
жиындарының тек біреуіне ғана кіретін болса, онда
жиынының (бүркеудің) элементтері өзара қиылыспаса, яғни А-ның әр элементі А
і
жиындарының тек біреуіне ғана кіретін болса, онда
 бүркеуі бөліктеу деп аталады.
бүркеуі бөліктеу деп аталады.
∀I, j∈I i≠j =>A i ∩A j =∅
Мысалы
Айталық А={1, 2, 3} болса, онда {{1, 2}, {2, 3}, {3, 1}} - А жиынын бүркейді, ал {{1}, {2}, {3}} - А жиынының бөліктеуі (бүркеуі де) болады.
Жиындарға қолданылатын операциялардың
Қасиеттері
Айталық U универсумы берілсін. Олай болса ∀ А, В, С⊂U төмендегідей қасиеттер орындалады:
∩, ∪ операцияларының ассоциативтігі:
- A∪(B∪C) =(A∪B) ∪C
A∩(B∩C) =(A∩B) ∩C ассоциативті (теру)
- ∪, ∩ операцияларының коммутативтігі
A∪B=B∪A
A∩B=B∩A (орын ауыстыру заңы)
- Идемпотенттік заң
A∪A=A
A∩A=A идемпотенттілік заңы
- Дистрибутивті заңдылық (үйлестіру заңы)
A∪(B∩C) =(A∪B) ∩(A∪C)
A∩(B∪C) =(A∩B) ∪(A∩C)
- Жұтылу заңы
A∪(A∩B) =A
A∩(A∪B) =A
- Де Морган заңы
=
Equation. 3
,
Equation. 3 =
Equation. 3
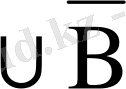
- Нөл мен бір заңы
Айталық 0⇆∅, 1⇆U онда
А∪∅=A; A∩∅=∅;
A∪1=1; A∩1=A;
A∪
=1; A∩
=∅
- Қос терістеу заңы (инволютивность)
- Толықтыру қасиеті
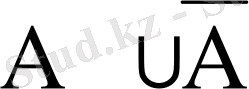
;
Equation. 3
∅
10. Айырым үшін өрнек: А\В=
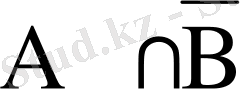
Қасиеттердің дәлелдемелері
Дистрибутивті заң (үйлестіру заңы)
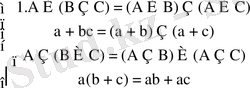
1 - ∩-қиылысуға байланысты сол жақтан бірігу ∪
2 - ∪-бірігуге байланысты сол жақтан қиылысу
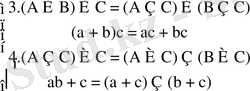
3 - ∪-бірігуге байланысты оң жақтан қиылысу ∩
4 - ∩-қиылысуға байланысты оң жақтан бірігу
Бұл теңдіктердің дұрыстығына бірнеше тәсілдермен көз жеткізуге болады:
- Нақтылы жиындар мен амалдарды орындау арқылы; (екі жағынан бірдей нәтиже шығады)
- Венн диаграммасын сызу арқылы;
- Амалдардың анықтамасын пайдалану арқылы.
1. Әдіс Нақтылы жиындар берілсін:
U={a, b, c, d, e}; A={a, b}; B={a, c, d}; C={b, c, d, e}
1-дәлелдейік:
Теңдіктің сол жағындағы амалдарды орындайық:
A∪(B∩C) ={a, b}∪({a, c, d}) ∩{b, c, d, e}={a, b}∪{c, d}={a, b, c, d};
(A∪B) ∩(A∪C) =({a, b}∪{a, c, d}) ∩({a, b}∪{b, c, d, e}) ={a, b, c, d}∩{a, b, c, d, e}=
{a, b, c, d};
бұдан A∪(B∩C) =(A∪B) ∩(A∪C) ;
2. Әдіс
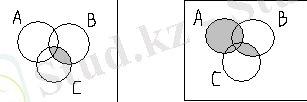
B∩C A∪(B∩C)
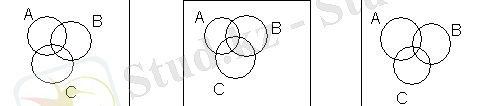
A∪B A∪C (A∪B) ∩(A∪C)
Жиындардың Декарт көбейтіндісі
х 1 . . . х n n элементтен тұратын реттелген тізбекті (x 1 , x 2 , …, x n ) немесе <x 1 , x 2 , …, x n > деп белгілеуге болады.
Мұндағы дөңгелек, бұрышты жақшалар элементтердің жазылу ретін көрсету үшін ғана қолданылады. Мұндай нөмірлерінің ретіне қарай орналасқан тізбек ұзындығын реттелген тізбек немесе ұзындығы n болатын кортеж деп аталады.
Мысалдар
- {a, b, c} және {1, 2} жиындарынан ұзындығы 2-ге тең 6 кортеж құруға болады:
(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)
- Кез-келген әріптерден құралған сөз кортеж натурал сандардың ондық жүйедегі жазылуы цифрлардан тұратын кортеж т. б.
- Кез-келген координаттары әртүрлі реттелген ақырлы жиын кортеж.
Ұзындығы 2-ге тең кортеждер реттелген жұптар, ұзындығы 3-ке тең кортеждер реттелген үштіктер, ұзындығы n-ге реттелген n-діктер деп аталады. Жиындар екі элементпен алу амалының көмегімен төмендегі ережеге сәйкес кодталады.
<>⇋∅, <x 1 >⇋x 1 , <x 1 , x 2 >⇌{{x 1 }, {x 1 , x 2 }},
<x 1 , …, x n >⇌<<x 1 , x 2 , …, x n >, x n+1 >
Анықтама Екі кортеж ұзындықтары бірдей, әрі бірдей нөмірлі координаттары тең болса ғана тең болады.
Яғни x=(x 1 , x 2 , …, x n )
y=(y 1 , y 2 , …, y n )
x=y егер x 1 =y 1 ; x 2 =y 2 , …x n =y n
Мысалы (1
2
, 2
2
, 3
2
) және ()
 Equation. 3
Equation. 3
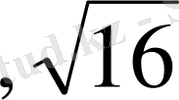
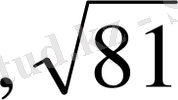 кортеждері тең
кортеждері тең
(1, 2, 3) және (3, 1, 2) әртүрлі
(1, 2, 3) және (1, 2, 3, 4) әртүрлі
(1, 2) ≠(2, 1)
ал {1, 2} және {2, 1} жиындары тең
Кортеждердің координаттары жиын болуы кортеж т. б. мүмкін. Мысалы,
({a, b}, c) және ({b, a}, c) тең
себебі {a, b}={b, a}
ал ((a, b), c) және ((b, a), c) кортеждері тең емес
себебі (a, b) ≠(b, a)
Бір де бір координаты жоқ кортеж (ұзындығы 0) бос кортеж деп аталады.
Сонымен жиын мен кортеж ұғымдарының айырмашылығы:
а) жиындардың элементтерінің орны, реті бәрі бір, ал кортеждерде элементтерінің ұзындығы бірдей болып элементтерінің реті басқаша болса әртүрлі (құрамы бірдей болса да) ;
б) жиында элементтер әртүрлі, кортежде бірдей бола береді.
Анықтама
А 1 , A 2 , …, A n жиындарының Декарт көбейтіндісі деп
{(x 1 , x 2 , …, x n ) x 1 ∈A 1 , x 2 ∈A 2 , …, x n ∈A n } жиынын айтамыз. Декарт көбейтіндісі A 1 *A 2 *…*A n болып белгіленеді. Әр түрлі жиындар элементтерінен құралған жиын Декарт көбейтіндісі деп аталады.
Егер A 1 =A 2 =…=A n =A болса, онда A 1 *A 2 *…*A n жиыны А жиынының n-ші Декарт дәрежесі деп аталады және А n болып белгіленеді.
Анықтама бойынша A 0 ⇌{∅}
1-мысал
A={1, 2}, B{3, 4}
A*B={(1, 3), (1, 4), (2, 3), (2, 4) }
B*A={(3, 1), (3, 2), (4, 1), (4, 2) }
A*A={(1, 1), (1, 2), (2, 1), (2, 2) }
Бұл мысалдардан A*B≠B*A
2-мысал (Шахмат тақтасы)
A={a, b, c, d, e, f, g, h}
B={1, 2, 3, 4, 5, 6, 7, 8}
Берілсін. Олай болса әр (х, у) жұбына x, y∈A*B шахмат тақтасының торлар жиыны сәйкес келеді.
3-мысал [0, 1] 2 жиыны{(a, b) 0≤a≤1, 0≤b≤1}
Бұл жиынға жазықтықтың 1-ден аспайтын теріс емес координаттары бар нүктелер жиыны сәйкес келеді.
Мысалдар
- A={a, b, c}
B={1, 2}
A*B={(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2) }
B*A={(1, a), (2, a), (1, b), (2, b), (1, c), (2, c) }
A*B≠B*A
- x={1, 2, 3}
x*x={(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3) }
A*B*C, (A*B) *C, A*(B*C) жиындары да әр түрлі.
A*B*C-(a, b, c)
(A*B) *C-((a, b), c) a∈A, b∈B, c∈C
A*(B*C) =(a, (b, c) )
Егер А, В жиындарының бірі бос болса, олардың Декарт көбейтіндісі де бос деп есептеледі.
A*∅=∅*A=∅*∅=∅
Мысал, А={a 1 , a 2 , a 3 }, B={b 1 , b 2 , b 3 }
A*B a 1 b 1 a 1 b 2 a 1 b 3
a 2 b 1 a 2 b 2 a 2 b 3
a 3 b 1 a 3 b 2 a 3 b 3
Сәйкестік. Функциялар мен бейнелеулер.
Эквиваленттік.
Сәйкестіктер - жиын элементтерінің арасындағы өзара байланысты беру тәсілі. Оның дербес жағдайлары: функциялар, бейнелер, бүрлендірулер, т. б.
Анықтама А, В жиындарының арасындағы сәйкестік деп бұл жиындардың тура (декарт) көбейтіндісінің G ішкі жиынын айтады
G≤A*B Егер (a, b) ∈G болса
δ G ={a(a, b) ∈G} G сәйкестігінде b a-ға сәйкес деп айтады
ρ G ={b(a, b) ∈G}
G - сәйкестігінің қасиеттері G⊆A*B
Анықтама Егер δ G =A болса толық анықталатын сәйкестік, δ A ⊆A болса толық емес (жартылай) сәйкестік болады. (толық анықталмаған)
Аеықтама Егер ρ G =B - сюръективті сәйкестік деп аталады. (В-ның әрбір элементінің А прообразы бар)
Анықтама G сәйкестігіндегі a∈A сәйкес барлық b∈B a элементтерінің образы, ал b∈B сәйкес келетін барлық a∈A b элементтерінің жиынындағы прообразы деп аталады.
Анықтама Егер анықталу облысынан δ G алынған кез-келген а элементінің ρ G мәндер жиынында бір ғана образы b∈ρ G болса G - функционал (бір мәнді) сәйкестік деп аталады.
Анықтама Егер G сәйкестігі үшін
- толық анықталған
- сюръективті
- функционалды
- ∀ b∈ρGэлементін, анықталу облысынан бір ғана a∈δGэлемент прообраз болса, онда G өзара бір мәнді сәйкестік болады.
Егер А мен В жиындарының арасында өзара бір мәнді сәйкестік болса, онда олардың қуаттары тең.
A=B - бұлар тең қуатты жиындар деп аталады.
Бұл фактілер екі жиынның элементтерін санамай-ақ қуаттарының теңдігін, қуатын санауға болатын жиынмен өзара бір мәнділігін дәлелдеу арқылы жиынның қуатын анықтауға болады.
N натурал сандар жиыны мен тең қуатты жиындар саналатын (счетные) жиын деп аталады.
R нақты сандар жиынымен тең қуатты сандар континуальды деп аталады.
1 мысал
Айталық G
G={(x, y) x, y∈ үшін (x-3) 2 +(y-2) 2 ≤1}
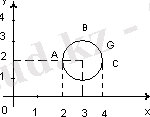
G - дөңгелегі R мен R арасындағы сәйкестік
а) 2, 3, 4 сандарының обраөы мен прообраздарын табу керек.
2∈δ G G сәйкестігіндегі образы жалғыз ғана 2∈ρ G
3-ң образы: G сәйкестігіндегі образы у осіне [1, 3]
4-ң образы G сәйкестігінде 2.
2∈ρ G прообразы - [2, 4] ⊆δ G
3∈ρ G G сәйкестігіндегі прообразы 3∈δ G
4∈ρ G - G сәйкестігінде прообраздары жоқ.
б) 1) [2, 3] ∈δ G сандарының образы осы ке сіндідегі барлық сандардың образдарының бірігуі, яғни [1, 3] ⊂ρ G
2) Осыған ұқсас [2, 4] G сәйкестігі образы [1, 3]
3) [2, 3] - прообразы:
[2, 3] ⊂ρ G прообразы [2, 4]
[2, 4] ⊂ρ G прообразы [2, 4]
Егер G сәйкестігі нақты сандар жиынында аныгқталатын десек, яғни G⊆R*R онда
- G - толық анықталмаған себебі δG≠R (δG⊂R)
- Сюръективті емес себебеі ρG≠R (ρG⊂R)
- Функционалды (бір мәнді) емес, себебі [2, 4] =δGүшін (2 мен 4-тен басқа) образдар жалғыз емес.
Егер сәйкестік G⊆[2, 4] *[1, 3] болса
- толық анықталған δG=A
- сюръективті ρG=B
бірақ функционалды және өзара бір мәнді емес.
2 мысал Айталық G - x-2=y x, y≥0
G={(x, y), x-2=y, x, y≥0}
G={әр түзудің элементтері x-2=1 қатынасын қанағаттандыратын нүктелер жиыны}
G - сәйкестігінің қасиеттері қандай?
G - нақты сандар жиынында берілген сәйкестік болса, G⊆R*R;
- Толық анықталмаған сәйкестік, себебі G=[2, ∞] ⊂R;
- Сюръективті емес, себебі G=R+=[0, ∞]
- Функционалды, себебі ∀ x∈δG, ρG- анықталу облысының барлық оң нақты санын бір ғана y∈ρGсәйкес (х-ң бір ғана сандар жиыны образы бар) нөлмен қоса.
- Өзара бір мәнді емес, себебі толық анықталуы сюръективтік орындалады.
Функциялар және бейнелер
Осы уақытқа дейінгі біз білетін функция анықталатын жиынды жиынға бейнелеудің дербес жағдайлары болып табылған.
Мат анализден функцияның анықтамасын білеміз.
Айталық, Х - сандар осінен алынған жиын болсын. Егер әрбір х∈Х нақтылы бір сан сәйкес келсе, онда бұл жиында f функция анықталған делінеді y=f(x) . Х - анықталу облысы, У - мәндер облысы.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz