Екінші ретті қисықтар: эллипс, гипербола және параболаның канондық және полярлық теңдеулері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

Екінші ретті қисықтар

Осы уақытқа дейін біздер х, у, г айнымалыларының тек бірінші дәрежеде болып келгсн жағдайларды, яғни түзулер мен жазықтықтардың әртүрлі теңдеулерін қарастырдық. Алдағы уақытарда олардың бірінші дәрежелерімен қоса, екінші {х ^г , ху, у ^г ) дәрежелері болып келген жағдайларды қарастырамыз. Олардың кейбіреулерін мектеп қабырғасында кездестірдік: кіндігі бас нүктеденемесе тік бұрышты декарттық координаталар жүйесіндегі кез келген {х _а , у„) нүктесінде жататын радиусы я болатын шеңбердід тсңдсулері- х ^: +у- ^й ^? (^х-х^+іу-уъУ =й') ; төбесі бас нүктеде немесе кезкелгсн (^. у») нүктссінде жататыи парабола теңдеудері у-ах- [і'-і/ _в =<і(х~хл ² ) ; гипербола теңдсулері - у = ~ және олардың сәйкес графиктері құрайық. Ол үшін жазықтықтағы қиындысына пайда болған тұйық қисық - эллипс; егерде жазыктық, конустың екі қуысына да карасты жасаушыларды қиып ететін болса (3. 21' д-сурет) - гипербола; ал жазықтық конустардың бір жасаушысына (мысал үшін, лв) параллель қоятын болса (3. 21 т~ сурет), опда қиылысында пайда болған қисық - парабола деп аталады. Егер жазықтық горизонтқа параллель О нүктесінен басқа жердең қиятың болса, қиындысына. шсңбер болатындығы ақиқат.

1. Эллипс. Фокустары дед аталатын екі нүктеден (Ғ _Х ., Ғ ₂ ) ара қашықтығы тұрақты (2о) шамаға. тең болатын, жазықтықтағы нүктелердің

геометриялық орны эллипс деп аталады.

Ескерту. Дербес жағдайда, Ғ _у = /•;, яши фокустары уйлескен болса, эллипс - шеңберге айналады. Енді эллипстің каиондьгқ тевдеуін

Ал күнделікті тіршілікге ондай қисықтардьш, алуан түрлері іздесетіндігі мөлім. Сапардың кейбіреулсріпс тоқталайық.

Мысал үшін, төбелері бір О нүктесінде үйлескен дөи^елск екі конусты өр түрлі орналасқан жазықтықтармсн (О нүктесінен басқа) жерінен қиған кездсгі, қиылысында пайда болатын қисықтардың турлерін қарастырайық (3. 21-сурет) .

Егер көлбеу жазықтық, конустың бір жақ қуысының барлық жасаушыларын толығымен қиып отетін болса (3. 21 /-сурет), онда

Гиперболаның канондық (3. 42) теңдеуінің, оның ағымдық нүктелері

үшін, у = ±~-<1х>~а'- - болатындығы бслгілі, Енді түзу бойындағы нүктслердің ординаталары мен гипербола ординаталарын бағалайық:

Бұдан х->±со кезде І?"-^* -- ~- монотонды кемімелі шама жене

X + \'Х~ -Л

ол нөлге ұмтылады. Демек, гипербола бойында жатқан Щх. у) нүктесімен г*±-х гүзуі бойында жатқан м'(х, у") нүктесі арасыидағы

қашықтық нөлге үмтьшатывдығын көреміз. Онда ү = ±-х түзуі (3. 42)

а

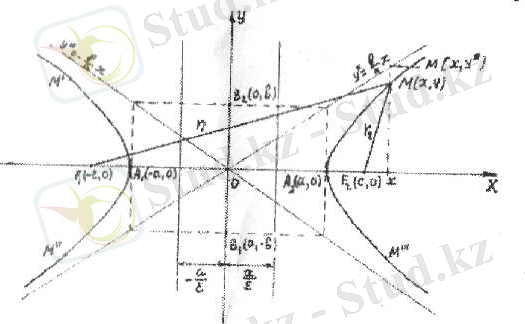
гипербола асимптотаеы болып табыладьЕ (3. 24-сурет) .

Ескерту. Келтірілген 3. 24-суреттен гипербола тармақтары Оу осімсн еш жердс қиылыспайды, сондықтан ол жорамал өсь деп

атадады.

3. Парабола. Фокусы деп аталатын ңүктесіне^ және • директриса деп аталаіын бір түзуден ^> Э>зак, ашықтықтары тсң болатын, жазықтықтағы нүктслердің геометриялық орны парабола дсп аталады.

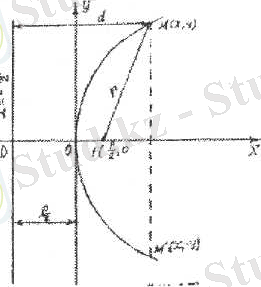
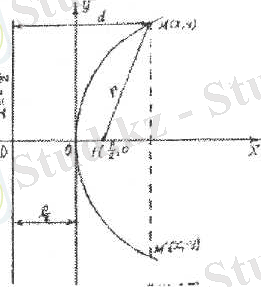
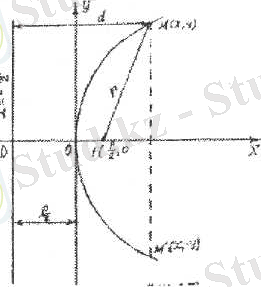
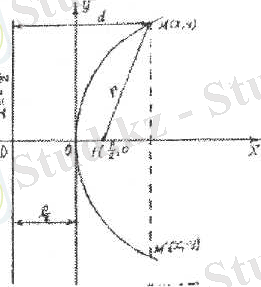
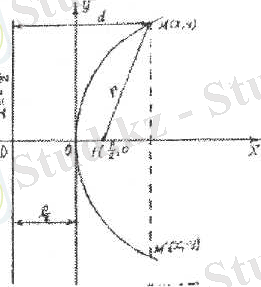
Параболаның канондық тегщсуін қүру үшін декартты: координаталар жүйссінің бас нүктесіи Ох өсінде жатқан ғі кссіндісінін ортасына орналастырайық (3. 25-сурет) .

Енді анықтама бойынша, мысал үшіп Л~, 0[, д-=~- болса

\2 ) 2

сі=ҒМ

Мұндағы

й? = £ + х, РМ = г = Л(х-£у+у ^я .

Енді (2) өрнектерді (1) -ге апарып қойсақ

- {х ~---) '-Ү у =>£- + иг+дс' =

2 4 '

- х ² - рх+ -- + у ^г --=> У=-2рх. (3. 43)

- параболаның каноқдык тсндеуін аламыз.

Параболаның канондық

теңдеуінен, М(х, у) нүктесі мен М'(х~у) нүктесі Ох - абсцисса өсіне қарағанда симметриялы, демек парабола Ох осіне симметриялы болады.

Келтірілген 3. 25-суреттсн: О{0, 0) -

г , . Ч

парабола төбесі; Ғ\ --, о I - фокусы; г - фокалдық радиусы, у--- іү^у*

бисектрисасы; парабола фокусынан директрисага дейінгі қашықтык - р , параболаның параметр! деп аталады. Егер парабола параметр] р>о {р<0) болса, онда парабола тармағы Оу өсінІң он,

(сол) жағына орналасады.

Егерде эллипстің, гяперболаның кіндігі жөне парабола тобесі бас нүктеде емсс, декарттық координатадар жүйесіндегі М ₉ (х _а , у ₉ ) нүктесінде орналасқан болса, онда олардың (3-41), (3. 42), (3. 43) канондьіқ тевдеулері, сәйкес:

І^ЗіИ ₊ ^--Уо) ³ ₌ _1; (3. 41 *)

а' Ь ²

і£ііі2і„СуіЛІІ _я і _: (3. 420

. де. картгак коорди катал ар жүйеаііің бяс нүктесін Қ(-с _х О) жөне Ғ, (+с$) нүктелерініц дол ортасыңда жататындай стіп а/іайық (3. 22-сурет) . Суреттс көрсетілгендей \Р^-' ₂ \ - 2с, \Ғ, м\ - г, , \Ғ ₂ М\= г ₂ .

ЭллипстІд анықтамасы бойьшша

г, + г, = 2л

ЭллипстІд анықтамасы бойьшша

г, + г, = 2л.

Мұңдағы,

/; -л/і^ ^+с ') ^? ⁺ >' ⁵ . '"і ~ у(-\'~ ^с ) "' -һ_к ² - (2)

Онда (I. ) мен (2>-ні лайдаланып,

<г^^(х--; -с) ^: + у ^! һ _% ) {х~с'г + у^ -■ 2й^> у(лч с) " і-У = 2а--7(*-с) '+У => -- ^ (д--і г:}' ч-У'~ 4а ^: ~4а^(х-с) ' і-) Г ±(х~с) ² +у ² =? , - г^. г" +2«+6'" +_у ^! ~ 4п ⁷ -<\а^{у-с) ¹ + у ² ¥х~ -2сх + е ² + у* =$ У г-^4сх-4а ^: --\а-^(х- с) ¹ -һу ² ~-> -(а" -сх) -ауСх-с) ¹ +> ² -^

Осы алынған (3. 41) теңдеу, эллйастіи канондық тсндеуі деп аталады.
Эллипстің (3. 38; канокдық тендеушеп оның бойьтнда жатқан кез
келген ағымдық ми. у) яуюгесіне, Оу, Ох өсьтеріне қарағанда
си мметриялы Ы '. м \ м - и у ктелері табылатындьігьщ көрсміз (3. 23-
сурст) . Мұндаіы: ^(0, 0) - эллипстің кнщігі;

/, (-й, о), Л(п. о), іг, (о, -й) . в ₂ (о, ь) - тебелері; 1-Х-сО) жоне Р" _а (+с, О) фокустары; г _іч г ₂ - фокалдық раднустары; о, * -сәйкес, үлкен жөне кіші

жарты өсьтері (2а, г&) - үлкер
және кіші өсьтері) .

с \а ¹ -іг \ 7

г -„ ₌ , -___. __ _тг і-- -• эксцеігг-

а \ а- X сг

рИСИТСТІ (£<] }; х~~±~-~ Қ ЖӘШ е

ь, фокустарына сәйкес

директрисалары дел аталады.

Жоғарьшагы 3. 23-суреттен эллипс бойында жататын нүктелер \ц < д, у < ь -- тік төрі бұрыш ішіне орналасатындыгын кореміз. Егердс А>« болса, о>іда эллипстің үлкен осі 2Һ, кіші всі (2я) болады, ал оның фокустары і\, К үлксн ось - 2Һ -ның бойына орналасады.

Ескерту. Егер (3. 41) эллипстің канондық тендеуіндегі улксн жонс кіші жарты өсьтері өзара тең (а = һ) болса, онда ( ) кіндіп бас нүктсде жататын, радиусы й-ге тең болатын шеңбердің тендеуін - г ^: + і--л- аламыз. Будан эллипстің, шсңберді Оу (немесе Ох) өсі бойынша кысылуынан павда болатындыгьЕіі көреміз.

2. Гипербола. Фокустары деп аталатын екі нүктсдсн (ғ,, ғ ₂ ) ара к:-ииык, тыктарынын, айырымының абсолют шамасы (модулі) түрақты [2а) шамаға тең болатьш, жазықтыктағы нүктелердің геометриялық

орны гипербола деп аталады.

Гиперболаның канондық теңдсуің күру үшін, тағы да 3. 22-оуретті карастырып, жоғарьщағы анықтаманы сске алайық, ятни

г, -г ₃ = 2а. (3)

Енді (2) өрнектерді (З) -кс қойып түрлендіру арқылы,

чііх+с) ¹ 4 у ¹ ~у] (х-с) ² +у ³ = 2а--> ^{х + с) ² -і- у ² -^{дг + с) ^: +у ² --^І{х--сУ'-+у ² г= ±2а =э ^/( х + с) ^г -і- у ² ~±2а + - у/р^- с) ² + у ^; => :^> (хі-с) ¹ +у ² =4а ³ ± 4йГд/(х - с) ~ +у ² +(х-с) ~ +у ² => -> у- ь2сх + с ^: л-у ¹ =■ 4а ^ъ ±Аа ^(х-с) ² л- у ¹ +х ¹ _і -2х с + с ¹ +у ⁷ ' ^> =р>ікд £"4йг = ±Ла^(х-с У + у ² т^х ¹ {сг -ег) -а ¹ у ^г = я ^г (с^ _- д ^: ) ^ --> [<:г -а ¹ = Ь'\^>һ'х ^г ~~а*у^ - і7"6' ^>

4-4 = 1 (3, 42)

а- Ь- - гнперболанын канондық тецдеуін аламыз.

Гиперболаның канондық тсндеуіндегі айнымалылар екінші дөрсжелі болғандықтан, өрбір ағьщдьпс, М(х, у) нүктесіне Ох, Оу ; өсьтеріне қарағанда симметриялы м'М'М" нүктелері табъшатындиғілн оцай керугс болады (3. 24-сурст) . Мұңдағы; : О(0, е) - гипербола кішцгі; л, (-а, о), л, (а, о) - ішқты тобелері; Қ{о, ~һ\ в _? (о, ь) -~ жорамал тоб е/ісрі; Қ(-с, 0), Ғ _? (-іс, 0) - фокустары; /;, ?■. - фокалдык ридиустары; Ох ~ накты осі; Оу -жорамал осі; у-±-х -

а

асимптоталары; & « - ■=■ /і + -- ■- эксңеіприситеті {е < 1) ; ү = і:~

а V а" е

лиректрисалары деп аталады. Жогарыдаіъі (3. 42) тендеуден жөне 3. 24-сурсттен, \х\ > а, ятни гипербола гармақтары г = -а тузуінің сол жагына, х = а тү-зуінің оң жагына орналасқан.

бүрыш ішіне орналасатындыгын кореміз. Егердс А>« болса, о>іда эллипстің үлкен осі 2Һ, кіші всі (2я) болады, ал оның фокустары і\, К үлксн ось - 2Һ -ның бойына орналасады.

Ескерту. Егер (3. 41) эллипстің канондық тендеуіндегі улксн жонс кіші жарты өсьтері өзара тең (а = һ) болса, онда ( ) кіндіп бас нүктсде жататын, радиусы й-ге тең болагын шеңбердің тендеуін - г ^: + і--л- аламыз. Будан эллипстің, шсңберді Оу (немесе Ох) өсі бойынша кысылуынан павда болатындыгьЕіі көреміз.

2. Гипербола. Фокустары деп аталатын екі нүктсдсн (ғ,, ғ ₂ ) ара к:-ииык, тыктарынын, айырымыныц абсолют шамасы (модулі) түрақты [2а) шамаға тең болатьш, жазықтыктагы нүктелердің геометриялық

орны гипербола деп аталады.

г, -г ₃ = 2а. (3)

Енді (2) өрнектерді (З) -кс қойып түрлендіру арқылы,

чііх+с) ¹ 4 у ¹ ~у] (х-с) ² +у ³ = 2а--> ^{х + с) ² -і- у ² -^{дг + с) ^: +у ² --^І{х--сУ'-+у ² г= ±2а =э ^/( х + с) ^г -і- у ² ~±2а + - у/р^- с) ² + у ^; => :^> (хі-с) ¹ +у ² =4а ³ ± 4йГд/(х - с) ~ +у ² +(х-с) ~ +у ² => -> у- ь2сх + с ^: л-у ¹ =■ 4а ^ъ ±Аа ^(х-с) ² л- у ¹ +х ¹ _і -2х с + с ¹ +у ⁷ ' ^> =р>ікд £"4йг = ±Ла^(х-с У + у ² т^х ¹ {сг -ег) -а ¹ у ^г = я ^г (с^ _- д ^: ) ^ --> [<:г -а ¹ = Ь'\^>һ'х ^г ~~а*у^ - і7"6' ^>

4-4 = 1 (3, 42)

а- Ь- - гнперболанын канондық тецдеуін аламыз.

Гиперболаның канондық тсндеуіндегі айнымалылар екінші дөрсжелі болғандықтан, өрбір ағьщдьпс, М(х, у) нүктесіне Ох, Оу ; өсьтеріне қарағанда симметриялы м'М'М" нүктелері табъшатындиғілн оцай керугс болады (3. 24-сурст) . Мүкдағы; : О(0, е) - гипербола кішцгі; л, (-а, о), л, (а, о) - ішқты тобелері; Қ{о, ~һ\ в _? (о, ь) -~ жорамал тоб е/ісрі; Қ(-с, 0), Ғ _? (-іс, 0) - фокустары; /;, ?■. - фокалдык ридиустары; Ох ~ накты осі; Оу -жорамал осі; у-±-х -