Туынды мен дифференциал: анықтамалар, дифференциалдау ережелері және қолданбалы есептер


Туынды. Дифференциалдау ережелері
Қандай да болса бір
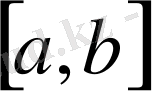 аралығында анықталған функция
аралығында анықталған функция
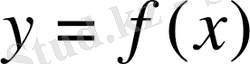 берілсін.
берілсін.
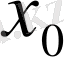 деп
х
-тің
деп
х
-тің
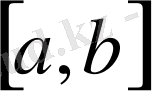 аралығында кез келген бір мәнін белгілейік. Аргумент
х
-тің бастапқы мәні
х
0
-ге
аралығында кез келген бір мәнін белгілейік. Аргумент
х
-тің бастапқы мәні
х
0
-ге
 өсімшесін берсек (
өсімшесін берсек (
 өсімшесі оң да, теріс те бола алады), аргументтің жаңа мәні
өсімшесі оң да, теріс те бола алады), аргументтің жаңа мәні
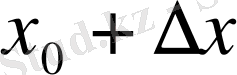 - ке келеміз. Аргументтің жаңа мәні де
- ке келеміз. Аргументтің жаңа мәні де
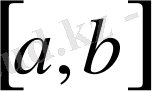 аралығында болуы тиіс. Сонда берілген
аралығында болуы тиіс. Сонда берілген
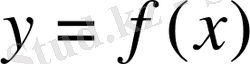 функциясы да жаңа мәнін қабылдайды, ол
функциясы да жаңа мәнін қабылдайды, ол
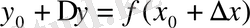
болады да, функцияның өсімшесі
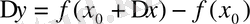
болады.
Сонан кейін функция өсімшесінің аргумент өсімшесіне қатынасын
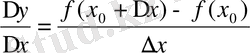
табамыз. Әрине, бұл қатынас
 -тің функциясы.
-тің функциясы.
Егер функция өсімшесінің өзінің пайда болуына себепші болған тәуелсіз айнымалының өсімшесіне қатынасының шегі болса, яғни
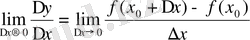
болса, бұл шек
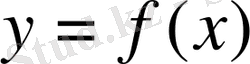 функциясының тәуелсіз айнымалы
х
бойынша алынған
х
0
нүктесіндегі туындысы деп аталады, оны
y’
немесе
функциясының тәуелсіз айнымалы
х
бойынша алынған
х
0
нүктесіндегі туындысы деп аталады, оны
y’
немесе
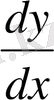 арқылы белгілейді, яғни
арқылы белгілейді, яғни
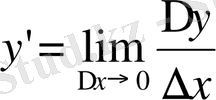
Белгіленген
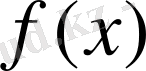 функциясының туындысы
функциясының туындысы
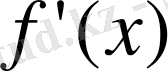 -ті іздеп табу амалы ол функцияны дифференциалдау деп аталады. Дифференциалдау ережелері мен туындылардың қасиеттері туралы ілім дифференциалдық есептеу деп аталады.
-ті іздеп табу амалы ол функцияны дифференциалдау деп аталады. Дифференциалдау ережелері мен туындылардың қасиеттері туралы ілім дифференциалдық есептеу деп аталады.
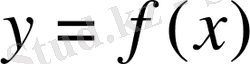 функциясы
х
0
нүктесінде үзіліссіз болу үшін ол функцияның сол нүктеде арқылы туындысы болуы жеткілікті.
функциясы
х
0
нүктесінде үзіліссіз болу үшін ол функцияның сол нүктеде арқылы туындысы болуы жеткілікті.
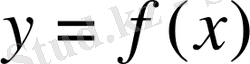 қисығының абсциссасы
х
0
-ге тең нүктесі арқылы жүргізілген жанаманың бұрыштық коэффициенті
f(x)
функциясының туындысы
қисығының абсциссасы
х
0
-ге тең нүктесі арқылы жүргізілген жанаманың бұрыштық коэффициенті
f(x)
функциясының туындысы
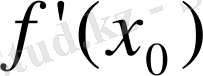 -ге тең болады, яғни
-ге тең болады, яғни
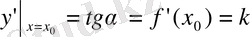
Демек,
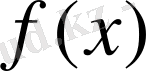 функциясының графигіне
х
0
нүктесінде жүргізілген жанаманың теңдеуі былай жазылады:
функциясының графигіне
х
0
нүктесінде жүргізілген жанаманың теңдеуі былай жазылады:
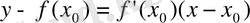
Сондай-ақ
х
нүктесіндегі функция өзгерісінің жылдамдығын және кез-келген
t
уақыт мезгілінде еңбек өнімділігін туынды деп түсінеміз, функцияның туындысы болу үшін
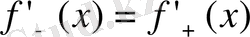 теңдігінің орындалуы қажетті және жеткілікті мұндағы
теңдігінің орындалуы қажетті және жеткілікті мұндағы
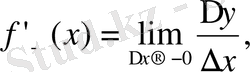
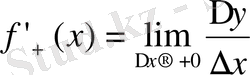
Егер
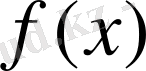 функциясының
х
нүктесіндегі туындысы шексіздікке тең болса,
функциясының
х
нүктесіндегі туындысы шексіздікке тең болса,
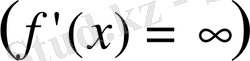 онда
y=f(x)
функциясының графигіне
х
нүктесінде жүргізілген жанама ОХ өсіне перпендикуляр болады.
онда
y=f(x)
функциясының графигіне
х
нүктесінде жүргізілген жанама ОХ өсіне перпендикуляр болады.
Егер u=u(x), y=y(x) туындылары бар функциялар болып, с=const болса, онда негізгі дифференциалдау ережелері төмендегідей болады:
1)
c’=0
2)
(u
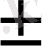 v) =u’
v) =u’
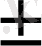 v’
3)
(cu) =cu’
v’
3)
(cu) =cu’
4)
(uv) =u’v+vu’
5)
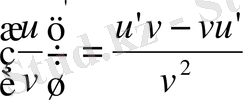 (
v
(
v
 0
)
0
)
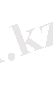
6) Егер
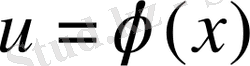 функциясы
х
0
нүктесінде дифференциалданса, ал
функциясы
х
0
нүктесінде дифференциалданса, ал
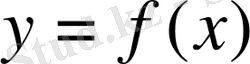 функциясы
функциясы
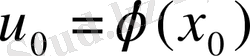 нүктесінде дифференциалданса, онда күрделі функция
нүктесінде дифференциалданса, онда күрделі функция
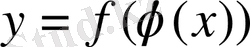 х
0
нүктесінде дифференциалданатын функция деп аталып, оның туындысы былай табылады.
х
0
нүктесінде дифференциалданатын функция деп аталып, оның туындысы былай табылады.
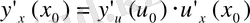
Элементар функцияларды дифференциалдау
1)
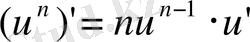 2)
2)
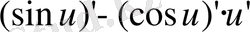
3)
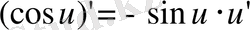 4)
4)
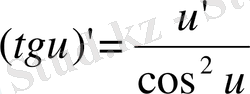
5)
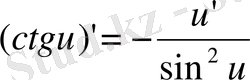 6)
6)
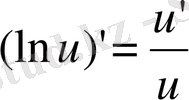
7)
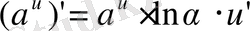 8)
8)
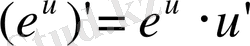
9)
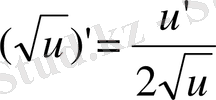 10)
10)
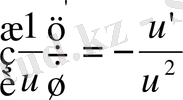
11)
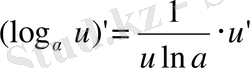 12)
12)
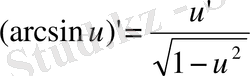
13)
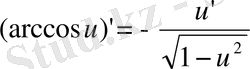 14)
14)
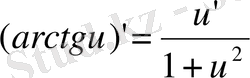
15)
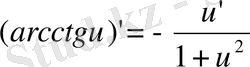
16) Егер: 1)
х
0
нүктесінде
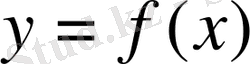 функциясының нөлге тең емес туындысы
функциясының нөлге тең емес туындысы
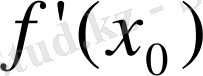 бар болса,
бар болса,
2) тура функция
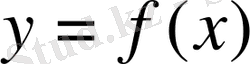 -ке кері функция
-ке кері функция
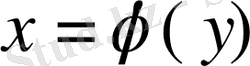 бар болса,
бар болса,
3) бұл кері функция
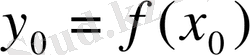 нүктесінде үзіліссіз болса, онда
нүктесінде үзіліссіз болса, онда
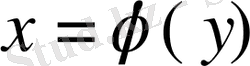 кері функцияның
кері функцияның
 нүктесінде туындысы бар және ол мына формула бойынша табылады:
нүктесінде туындысы бар және ол мына формула бойынша табылады:
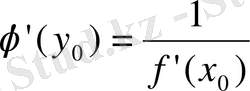
немесе
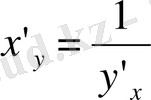
Мына
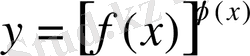
функцияны дәреже-көрсеткіштік функция деп атайды.
Бұл функцияның туындысын табу үшін логарифмдік дифлогарифм деп алып, соның нәтижесінде пайда болған функцияға ғана дифференциалдау ережелерін қолданады. Логарифмдік дифференциалдаудың нәтижесін логарифмдік туынды деп атайды.
Осы айтылған тәсілді қолдансақ:
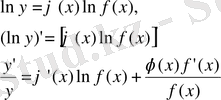
болады.
Демек,
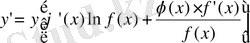
немесе
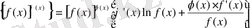
Бұл формуланы мына түрге келтіруге болады:
 (2. 2. 2)
(2. 2. 2)
(2. 2. 2) -нің оң жағындағы бірінші қосылғыш - берілген функцияны көрсеткіштік функция деп қарап, дифференциалдағанда, ал екінші қосылғыш - сол функцияны дәрежелік функция деп қарап, дифференциалдағанда шығатын нәтиже.
Төмендегі айқындалған функцияладың туындыларын табыңдар:
1.
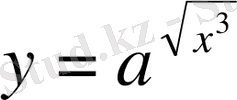
Шешуі:
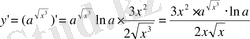
2.
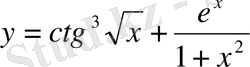
Шешуі:
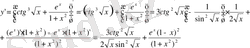
3.
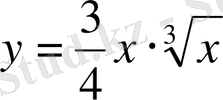
Шешуі:
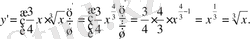
Айқындалмаған функцияның туындысын табу
Егер х пен у -тің арасындағы байланыс айқындалмаған түрде, мына
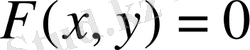
теңдеумен берілсе, онда
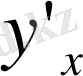 туындысын табу үшін:
туындысын табу үшін:
- теңдеудегіу-тіх-тен тәуелді функция деп қарап, теңдеудің сол жағынанхбойынша туынды алу керек;
- осы туындыны нөлге теңестіру керек, яғни
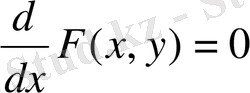
- алынған теңдеудіарқылы шешу керек
- а) Мына
айқындалмаған функцияның туындысын тап?
Шешуі:
Берілген теңдеуде
х
бойынша дифференциалдап
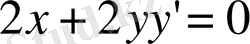 теңдеуін табамыз.
теңдеуін табамыз.
Бұдан
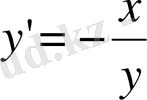
б)
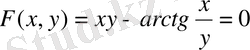
айқындалмаған функцияның туындысын табу керек.
Шешуі:
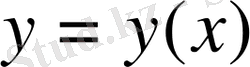 функциясы айқындалмаған
функциясы айқындалмаған
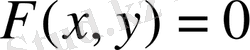 теңдеуімен беріліп тұр. Сондықтан
теңдеуімен беріліп тұр. Сондықтан
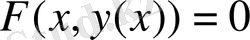 теңбе-теңдікті күрделі функция ретінде
х
аргументі бойынша дифференциалдап, сонда шығатын теңдеуден
у’
туындысын шығарамыз, яғни
теңбе-теңдікті күрделі функция ретінде
х
аргументі бойынша дифференциалдап, сонда шығатын теңдеуден
у’
туындысын шығарамыз, яғни
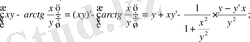
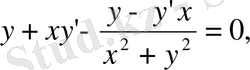
Бұдан
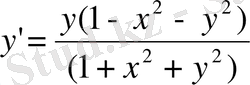
Жоғары ретті туындылар
Шектеулі
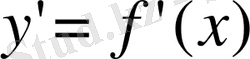 туындысы бар
туындысы бар
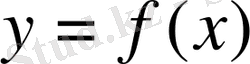 функциясын қаралық. Бұл
функциясын қаралық. Бұл
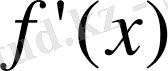 тундысының өзі тәуелсіз айнымалы
х
-тің функциясы болып табылады, сондықтан одан тағы да
х
бойынша туынды алуғы болады. Сонда
тундысының өзі тәуелсіз айнымалы
х
-тің функциясы болып табылады, сондықтан одан тағы да
х
бойынша туынды алуғы болады. Сонда
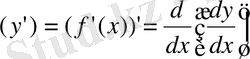
Әдетте, бұл былай жазылады:
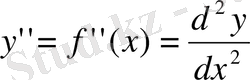
Бірінші туындының туындысын екінші ретті туынды немесе
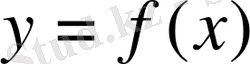 функциясының екінші туындысы дейді:
функциясының екінші туындысы дейді:
Осы сияқты:
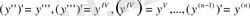
туындыларын табуға болады.
Егер нүктенің түзу сызық бойымен қозғалысының заңы
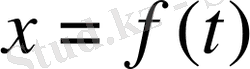 теңдеуімен берілсе, онда
теңдеуімен берілсе, онда
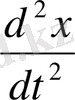 осы қозғалыстың үдеуін анықтайды.
осы қозғалыстың үдеуін анықтайды.
- Мына
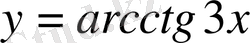
функциясының екінші ретті туындысын тап?
Шешуі: ең алдымен осы функциядан бірінші туындыны табайық:
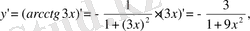

- Мына
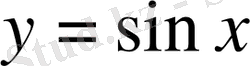
функциясының п -ші ретті туындысын табу керек
Шешуі: Бұл функцияның туындыларын біртіндеп табамыз:
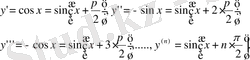
Мысалы,
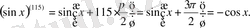
Қисыққа жүргізілген жанама туралы есептер
Біз
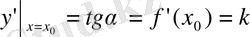 және
және
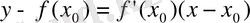 формулаларының көмегімен мысалдар шығарайық:
формулаларының көмегімен мысалдар шығарайық:
Шешуі:
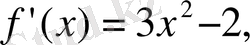
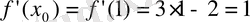
Олай болса:
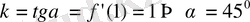 .
.
2.
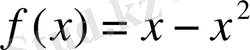 функциясының графигіне абсциссасы
функциясының графигіне абсциссасы
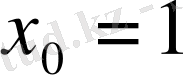 нүктесінде жүргізілген жанама
ОХ
өсімен қандай бұрыш жасайды?
нүктесінде жүргізілген жанама
ОХ
өсімен қандай бұрыш жасайды?
Шешуі:
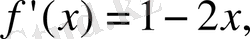
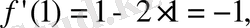
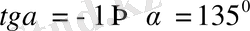
3.
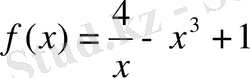 функциясының графигіне абсциссасы
функциясының графигіне абсциссасы
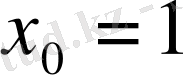 нүктеде жүргізідген жанаманың теңдеуін.
нүктеде жүргізідген жанаманың теңдеуін.
Шешуі:
Есептің шарты бойынша
 олай болса
олай болса
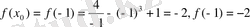
Енді туындыны тауып
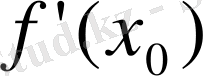 -ді есептейміз:
-ді есептейміз:
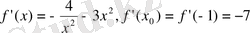 .
.
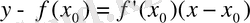 формуласын ескеріп
формуласын ескеріп
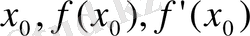 мәндерін қойсақ, онда іздеген жанаманың теңдеуі
мәндерін қойсақ, онда іздеген жанаманың теңдеуі
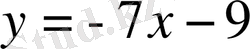 болады.
болады.
4.
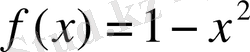 функциясының графигіне оның
О
өсімен қиылысу нүктесінде жүргізілген жанаманың теңдеуін жазыңдар.
функциясының графигіне оның
О
өсімен қиылысу нүктесінде жүргізілген жанаманың теңдеуін жазыңдар.
Шешуі:
Әуелі берілген функцияның графигінің
ОХ
өсімен қиылысу нүктесін табамы, ол үшін
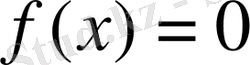 теңдеуін шешеміз:
теңдеуін шешеміз:
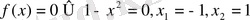
Сонымен, іздеп отырған нүктелер
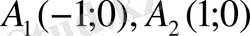
Енді
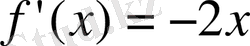 екенін ескерсек, онда
екенін ескерсек, онда
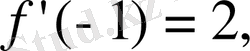 ал
ал
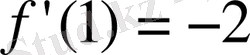 болады.
болады.
Демек
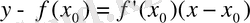 формуласы бойынша
формуласы бойынша
 және
және
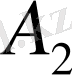 нүктелерде жүргізілген жанамалардың теңдеулері сәйкес мына түрде жазылады:
нүктелерде жүргізілген жанамалардың теңдеулері сәйкес мына түрде жазылады:
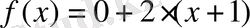 яғни
яғни
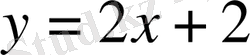
 яғни
яғни
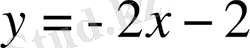
5.
Мына
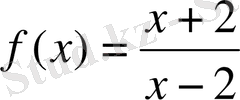 функциясының графигіне жүргізілген жанама
ОХ
өсімен қандай нүктеде 135
0
бұрыш жасайды?
функциясының графигіне жүргізілген жанама
ОХ
өсімен қандай нүктеде 135
0
бұрыш жасайды?
Шешуі: Іздеп отырған нүктелердің координаталарын мына теңдеуді шешіп анықтаймыз:
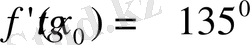 немесе
немесе
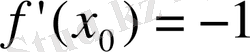
Мұндағы
 жанама жүргізілген нүктенің абсциссасы.
жанама жүргізілген нүктенің абсциссасы.
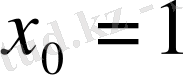
Сонда
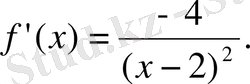
Енді
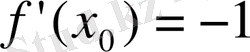 екенін ескеріп:
екенін ескеріп:
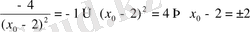
Демек,
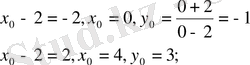
Жауабы: 1) (4; 3) және (0; -1) .
6.
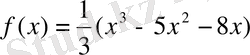 функциясының графигіне қандай нүктелерде жүргізілген жанама абсциссалар өсіне параллель болады?
функциясының графигіне қандай нүктелерде жүргізілген жанама абсциссалар өсіне параллель болады?
Шешуі:
Берілген функцияның графигіне жүргізілген жанама абсциссалар өсіне параллель болса, онда ол түзудің бұрыштық коэффиценті нөлге тең болады, яғни
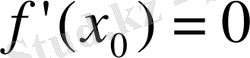 , мұнда
, мұнда
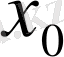 жанама жүргізілген нүктенің абсциссасы. Сонымен іздеп отырған нүктенің абсциссасын
жанама жүргізілген нүктенің абсциссасы. Сонымен іздеп отырған нүктенің абсциссасын
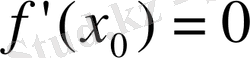 теңдеуін шешіп табамыз:
теңдеуін шешіп табамыз:
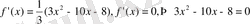
осыдан
 ,
,
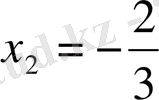 . Енді осы нүктелердің сәйкес ординаталарын табалық:
. Енді осы нүктелердің сәйкес ординаталарын табалық:
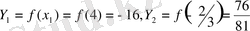
Сонымен жанама абсциссалар өсіне параллель болуы үшін ол мына нүктелерде жүргізілуі керек:
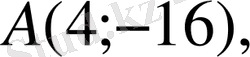
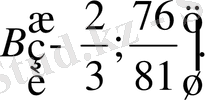
7.
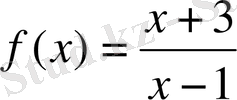 функциясының графигіне оның
OY
өсімен қиылысу нүктесінде жүргізілген жанаманың теңдеуін жазыңдар.
функциясының графигіне оның
OY
өсімен қиылысу нүктесінде жүргізілген жанаманың теңдеуін жазыңдар.
Шешуі: Әуелі ОY өсімен қиылысу нүктесін табалық.
Ол үшін
 деп қабылдап
деп қабылдап
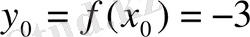 табамыз.
табамыз.
Енді жанаманың бұрыштық коэффицентіне табамыз:
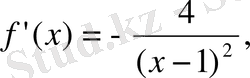
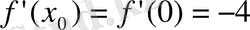
Олай болса (0; -3) нүктесінде жүргізілген жанаманың теңдеуі:

Функцияның дифференциалы
Анықтама:
Аргумент өсімшесі
 - ке сәйкес
- ке сәйкес
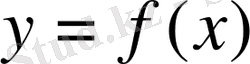 функцияның
функцияның
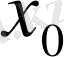 нүктесіндегі дифференциалы деп
нүктесіндегі дифференциалы деп
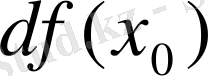 немесе
немесе
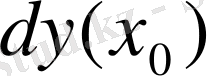 символдарымен белгіленетін
символдарымен белгіленетін
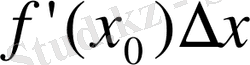 санын айтады.
санын айтады.
Сонда анықтама бойынша
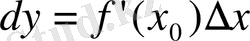
Егер
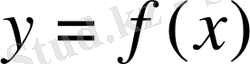 функциясы (
а, b
) интервалының кез-келген
х
нүктесінде дифференциалданатын болса, онда
функциясы (
а, b
) интервалының кез-келген
х
нүктесінде дифференциалданатын болса, онда
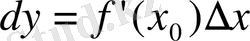 формула мына түрде жазылады:
формула мына түрде жазылады:
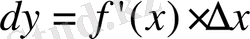
мұндағы
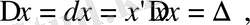 демек
демек
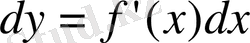
Мысалы:
- 6.
7.
8.
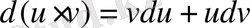
9.
10.
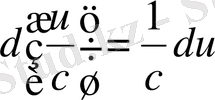
11.
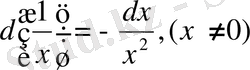
12.
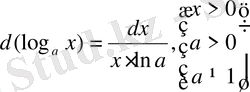
13.
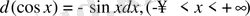
14.
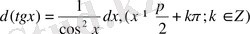
15.
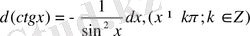
16.
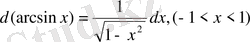
17.
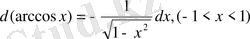
18.
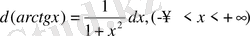
19.
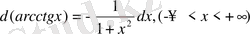
- Мына
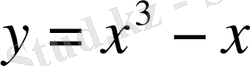
функциясының өсімшесі мен дифференциалын табыңдар.
Шешуі:
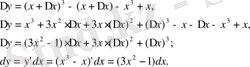
Берілген функцияның өсімшесі
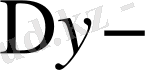 тің жуық мәні үшін оның дифференциалы
тің жуық мәні үшін оның дифференциалы
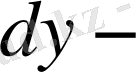 ті алуға болады, яғни
ті алуға болады, яғни

Сонымен
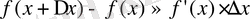
Айталық,
 функциясы берілсін. Оның өсімшесі
функциясы берілсін. Оның өсімшесі
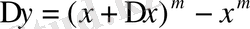
болады.
Бұдан
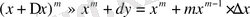
Егер
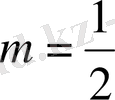 болса, онда
болса, онда
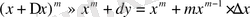 формула мына түрге келеді:
формула мына түрге келеді:
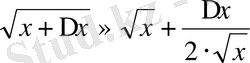
Егер
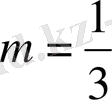 болса, онда
болса, онда
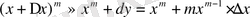 формула мына формулаға айналады:
формула мына формулаға айналады:
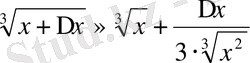
Осы сияқты, егер
 функциясы берілсе, онда
функциясы берілсе, онда
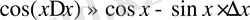
формуласын алуға болады.
Сонымен, дифференциалды жуықтап есептеуге қолданылады.
- өрнегінің жуық мәнін есептеңдер:
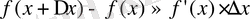 формуласын қолданайық:
формуласын қолданайық:
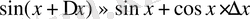
Сонда
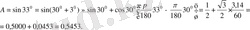
- өрнегінің жуық мәнін есептеңдер:
Шешуі:
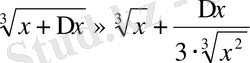 формуланың жәрдемі мен
формуланың жәрдемі мен
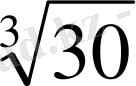 -ды былай жазалық:
-ды былай жазалық:
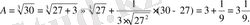
Осы сияқты
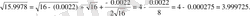
Лопиталь ережесі.
а)
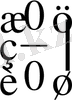 түріндегі анықталмағандықтарды айқындау.
түріндегі анықталмағандықтарды айқындау.
Егер
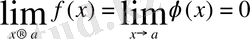 болса, онда
болса, онда
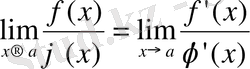
Егер соңғы шек
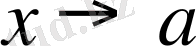 жағдайда тағыда
жағдайда тағыда
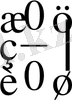 түрінде болса, онда осы процесті әрі қарай соза береміз, яғни шек анықталған мезгілде
х-
тің орнына мәнін қойып қорытынды шығарамыз.
түрінде болса, онда осы процесті әрі қарай соза береміз, яғни шек анықталған мезгілде
х-
тің орнына мәнін қойып қорытынды шығарамыз.
Лопиталь ережесі жоғарыда көрсетілген анықталмағандықты анықтау үшін, тек
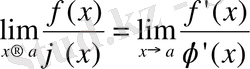 туындылар қатынасының шегі бар болғанда ғана қолданылады.
туындылар қатынасының шегі бар болғанда ғана қолданылады.
б)
Егер
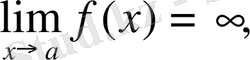
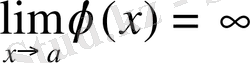 болса, онда
болса, онда
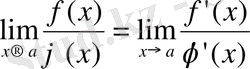
Әрине
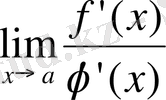 шегі бар болса, онда
шегі бар болса, онда
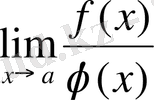 шегі де бар болады және
шегі де бар болады және
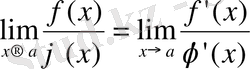 теңдігі орындалады.
теңдігі орындалады.
- Шекті табыңдар:
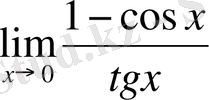
Шешуі:
Бұл шекте
 жағдайда
жағдайда
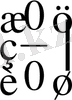 түріндегі анықталмағандық шығады. Сондықтан Лопиталь ережесін қолданамыз, яғни
түріндегі анықталмағандық шығады. Сондықтан Лопиталь ережесін қолданамыз, яғни
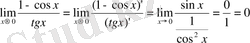
- Шекті табыңдар:
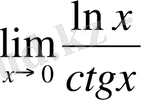
Шешуі: Бұл шекте анықталмағандықтың түрі
. Демек Лопиталь ережесін қолданамыз, яғни
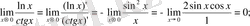
- Мына
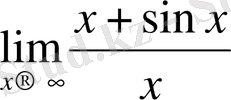
шекті табыңдар
Шешуі:
себебі
.
символдары да анықталмағандықтар деп аталады. Мысалы
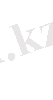
түріндегі анықталмағандықты
түріне келтіріп, онан кейін лопиталь ережесін қолдануға болады.
- Мына
шекті табыңдар.
Шешуі:

Біз
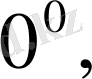
түрінде анықталмағандықтарды ашу тәсілдерін мысалдар арқылы түсіндірейік:
- Мына
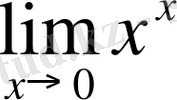
шекті табу керек.
Шешуі:
деп белгілейік те, оны логарифм десек,
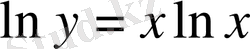
болар еді.
Демек,
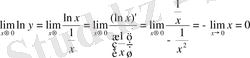
Олай болса,
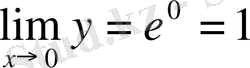
Сонымен
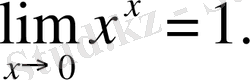
- Мына

шекті табыңдар.
Шешуі: Берілген функцияның шекті мәні
түріндегі анықталмағандықты береді.
Егер
деп белгілесек,
болар еді.
Бұдан:
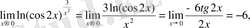
Сондықтан
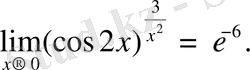
Функцияның өсуі мен кемуі
Егер
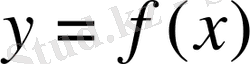 функциясы
функциясы
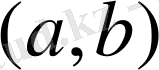 интервалында дифференциалданатын функция және барлық
интервалында дифференциалданатын функция және барлық
 үшін оның туындысы
үшін оның туындысы
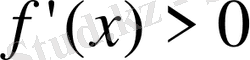
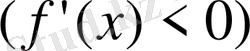 болса, онда осы интервалда
болса, онда осы интервалда
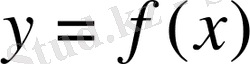 функциясы өспелі (кемімелі) болады.
функциясы өспелі (кемімелі) болады.
- Мына
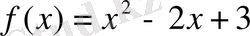
функцияның өсетін және кемитін аралығын табыңдар?
Шешуі: функцияның туындысын тауып, оны нөлге теңестірейік, яғни
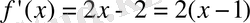
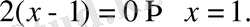
Сонда, сан түзуінде (-
; 1) және (1; +
) аралықтар табылады.
Егер
онда
. Сондықтан бұл аралықта
функциясы кемиді. Егер
, онда
. Демек берілген функция бұл аралықта өседі.
- Мына
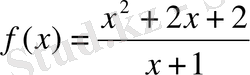
функцияның өсетін және кемитін аралықтарын табыңдар.
Шешуі: Берілген функция
ден басқа барлық х- тер үшін анықталған, яғни
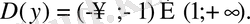
Функцияның туындысын табалық:
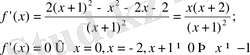
Егер
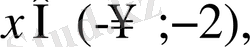 онда
онда
 Демек
Демек
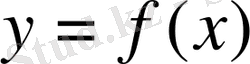 функциясы өседі.
функциясы өседі.
Егер
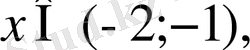 онда
онда
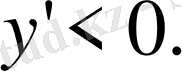 демек берілген функция кемиді.
демек берілген функция кемиді.
Егер
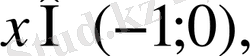 онда
онда
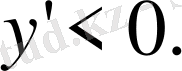 Сондай-ақ
Сондай-ақ
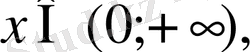 онда
онда
 Сонымен берілген функция
Сонымен берілген функция
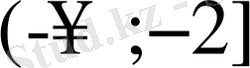 және
және
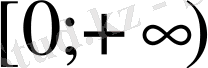 аралықтарда өседі, ал
аралықтарда өседі, ал
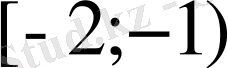 және
және
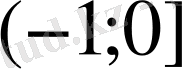 аралықтарда кемімеліболады.
аралықтарда кемімеліболады.
- Мына
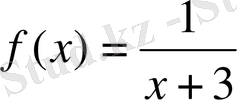
функцияның өсетін және кемитін аралықтарын табыңдар:
Шешуі:
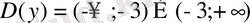
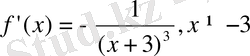
егер
болса. Сондықтан берілген
функциясы
және
аралығында кемімелі болады.
Функцияның экстремумдары
Айталық,
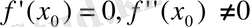 болсын. Сонда
болсын. Сонда
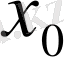 экстремум нүктесі болады. Сонымен бірге
экстремум нүктесі болады. Сонымен бірге
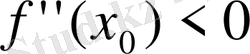 болғанда,
болғанда,
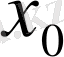 максимум нүктесі де, ал
максимум нүктесі де, ал
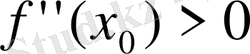 болғанда
болғанда
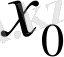 минимум нүктесі болады.
минимум нүктесі болады.
Мына төмендегі функцияларды экстремумға зерттеңдер:
Шешуі:
туындысын тауып, оны нөлге теңестіріп
түбірлерін табамыз, яғни
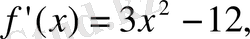
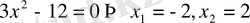
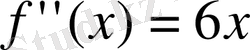
Сонда
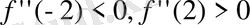
Демек, х=-2 нүктесінде
тің максимум,
нүктесінде - минимуиы бар болып шықты:
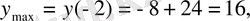
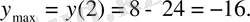
... жалғасыШешуі:
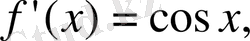
теңдеуінің түбірлері:
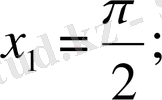
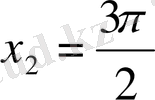
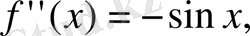
Сонда
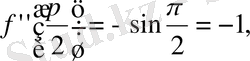
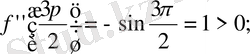
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz