Матрица және негізгі түсініктер: анықтамалар, операциялар, транспонирлеу және ранг


ҚММУ Ф 4/3-04/03
2007ж. 14 маусымдағы №6 НХ.
ҚАРАҒАНДЫ МЕМЛЕКЕТТІК МЕДИЦИНА УНИВЕРСИТЕТІ
Медициналық биофизика және информатика кафедрасы
ДӘРІС
Тақырыбы : «Матрица және негізгі түсініктер»
Қарағанды 2014ж.
Кафедра отырысында бекітілген
Хаттама № «»2014ж.
Кафедра меңгерушісі Б. К. Койчубеков
Тема:
Матрица және негізгі түсініктер
Мақсаты: Сызықтық алгебра элементтерінің негізгі түмініктерін енгізу, матрица түрлеріне түсінік беру, матрица рангі, кері матрица түсінігін қарастыру. Студенттердің теориялық білімдерін және есептер шешуде практикалық дағдыларын және медициналық сипаттағы есептерді шешуге қолдану негіздерін өңдеумен байланысты сызықтық алгебра бойынша білімдерін кеңейту жіне тереңдету.
Жоспар:
- Матрица түсінігі. Матрицаларға қолданылатын амалдар.
- Матрицаны транпонирлеу.
- Матрицаның рангі.
§ 1. Матрица түсінігі. Матрицаларға қолданылатын амалдар. Матрицаны транпонирлеу.
Анықтама:
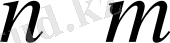 өлшемді матрица деп т жолдардан және п бағандардан құралған төртбұрышты сандар кестесінайтады. Матрицаны құрастыратын сандар матрица элементтері деп апталады.
өлшемді матрица деп т жолдардан және п бағандардан құралған төртбұрышты сандар кестесінайтады. Матрицаны құрастыратын сандар матрица элементтері деп апталады.
Матрица латын алфавитінің бас әрпімен белгіленеді, мысалы
А, В, С, …,
ал матрица элементтерін белгілеу үшін екі индексті кіші әріптер қолданылады:
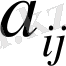 , мұндағы
, мұндағы
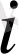 - жол нөмері,
- жол нөмері,
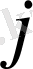 -баған нөмері. Матрица элементтері дөңгелек (кейде тік) жақшаға алынады.
-баған нөмері. Матрица элементтері дөңгелек (кейде тік) жақшаға алынады.
Мысал:

Қысқаша
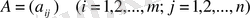 матрицасы түрінде белгіленеді.
матрицасы түрінде белгіленеді.
Мысал:

Матрица түрлері.
Анықтама: бір жолдан тұратын матрица, жол-матрица (жол-вектор), ал бір бағаннан - баған-матрица (баған-вектор) деп аталады.
 - жол-матрица,
- жол-матрица,
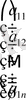 - баған-матрица.
- баған-матрица.
Мысал:
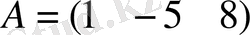 - жол-матрица,
- жол-матрица,
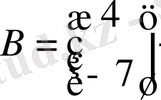 -баған матрица.
-баған матрица.
Анықтама: Егер матрица жолдарының саны баған сандарына тең болса, онда матрицаны квадраттық матрица деп атайды.
Мысал
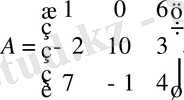 -
3-ші ретті квадраттық матрица.
-
3-ші ретті квадраттық матрица.
Анықтама: Егер матрицаның жол мен баған сандары сәйкеспесе, онда матрица тікбұрышты деп атайды.
Мысал:
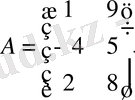 -
-
 өлшемді тікбұрышты матрица.
өлшемді тікбұрышты матрица.
Анықтама:
Жол және баған нөмерлері сәйкес болатын матрица элементтері бас диагоналды құрайды және диагоналды деп аталады. Квадраттық матрица үшін ба сдиагонал элементтері
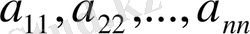 құрайды.
құрайды.
Анықтама: Егер квадрат матрицаның барлық диагональ емес элементтері нөлге тең болса, онда матрица диагональды деп аталады, яғни:
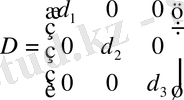
Мысал:
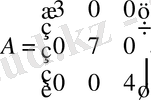 -
3-ші реті диагональды матрица.
-
3-ші реті диагональды матрица.
Анықтама: Егер диагональды матрицаның барлық диагональды элементтері бірге тең болса, онда матрица бірлік матрица деп аталады және Е әрпімен белгіленеді.
Мысал:
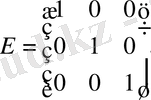 -
3-ші ретті бірлік матрица.
-
3-ші ретті бірлік матрица.
Анықтама: Кез келген өлшемді матрица нөлдік немесе нөл-матрица деп аталады, егер оның барлық элементтері нөлге тең болса.
 .
.
Анықтама : Бас диагоналы нөл болатын квадраттық матрица үшбұрышты матрица деп аталады.
Мысал:
 -
3-ші ретті үшбұрышты матрица.
-
3-ші ретті үшбұрышты матрица.
Анықтама : Матрицалар тең деп аталады, егер олардың жол және баған сандары бірдей болып және сәйкес орындарда тең сандар тұрса.
Матрицаға қолданылатын амалдар
1. Матрицаны санға көбейту
Анықтама:
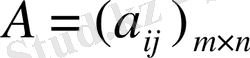 матрицасының
матрицасының
 санына көбейтіндісі деп
санына көбейтіндісі деп
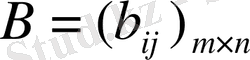 матрицасының әрбір элементтері,
матрицасының әрбір элементтері,
 санын
санын
 матрицасының сәйкес элементтерінің көбейтіндісіне тең матрицаны айтады:
матрицасының сәйкес элементтерінің көбейтіндісіне тең матрицаны айтады:
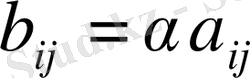 ,
,
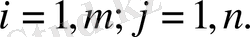
Мысал:
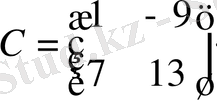 ,
,
 .
:
.
:
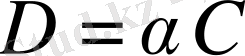 матрицасын табу.
матрицасын табу.
Шешуі :
 .
.
Салдар: Матрицаның барлық элементтерінің ортақ бөлгішін матрица белгісінің алдына шығаруға болады.
Мысал:
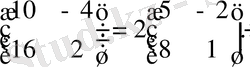
Салдар:
Матрицаның 0 санына көбейтіндісі нөлдік матрица.
2. Матрицалардың қосындысы
Анықтама: А және В бірдей өлшемді екі матрицаның қосындысы деп, А және В матрицалардың әрбір элементі сәйкес элементтердің қосындысына(айырмасын) тең болатын С=А+В матрицасын айтады:
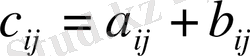 , где:
, где:
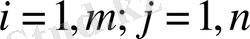
( яғни, матрицалар элементтері бойынша қойылады) .
Мысалы:
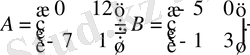 Онда:
Онда:
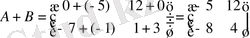 .
.
3. Матрицалар айырмасы
Бірдей өлшемді екі матрицаның айырмасы алдындағы амал арқылы анықталады:
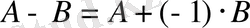 .
.
4. Матрицаларды транспонирлеу
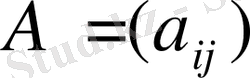 матрицасына транспонирленген матрица деп
матрицасына транспонирленген матрица деп
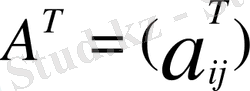 матрицасын айтады,
матрицасын айтады,
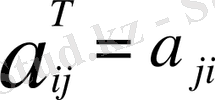 ,
,
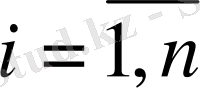 ,
,
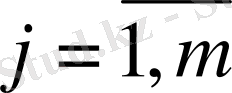 .
.
Матрицаны транспонерлеу . Қандай да бір А матрицасының жатық жолын сəйкес тік жол етіп жазғаннан пайда болған матрицаны берілген матрицаның транспонерленген
матрицасы деп атайды да , A¢ деп белгілейді. Берілген матрицаның өлшемі m x n болса, оның транспонерленген матрицасының өлшемі n x m болады.
Мысалы,
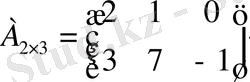
матрицасының бірінші жатық жолын бірінші тік жол етіп, ал екінші жатық жолын екінші тік жол етіп жазып оның транспонерленген матрицасын
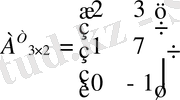 аламыз.
аламыз.
§ 2. Матрица рангі.
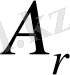 канондық матрицаның бас диагоналында тұрған
r бірлік саны
,
А
матрицаын канондық түрге келтіру тәсілінен тәуелсіз және ізделініп отырған
А
матрицасының
рангі
деп аталады:
r(A) = r
. Эквивалентті матрицаның бір ғана рангі болады.
канондық матрицаның бас диагоналында тұрған
r бірлік саны
,
А
матрицаын канондық түрге келтіру тәсілінен тәуелсіз және ізделініп отырған
А
матрицасының
рангі
деп аталады:
r(A) = r
. Эквивалентті матрицаның бір ғана рангі болады.
Анықтама: Матрицаның нолге тең емес минорларының ең үлкен реті матрица рангісі деп аталады: r=r(A) = rangA .
Матрица өлшемі артқан сайын оның рангісін барлық нолден өзге минорларды есептеу жолымен анықтау қиындайды. Матрица рангісін элементар түрлендірулер əдісімен табу, элементар түрлендірулер əдісі көмегімен А матрицасын сатылы түрге келтіріледі; сатылы матрицадан алныған нөлдік емес жолдар саны ізделініп отырған А матрицасының рангі.
А матрицасының рангін жиектелген минор әдісімен табу келесіден тұрады.
қажетті:
1. Қандайда бір М 1 бірінші ретті нөлден ерекше минорды табу керек (яғни матрица элементін) ; егер ондай минор жоқ болса, онда А нөлдік матрица және оның рангі r(A) = 0.
2. М
1
тұратын екінші ретті минорды есептеу (жиектелген М
1
), нөлден өзгеше М
2
миноры табылғанша. Егер ондай минор жоқ юолса, онда оның рангі
r(A) = 1
; егер бар болса, онда
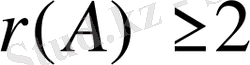 . Және т. с.
. Және т. с.
…
k. k-ші ретті минорды (егер олар бар болса) есептеу, жиектелген минор
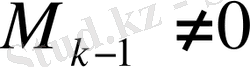 . Егер ондай минорлар жоқ немесе нөлге тең болса, онда
. Егер ондай минорлар жоқ немесе нөлге тең болса, онда
 , егер бар болса ең болмағанда бір
, егер бар болса ең болмағанда бір
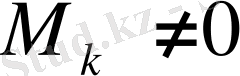 минор, онда
минор, онда
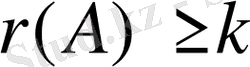 және есептеу жалғасады.
және есептеу жалғасады.
Матрица рангін табу кезінде мұндай тәсілмен k-ші ретті бір ғана нөлдік минорды әр қадамман табу жеткілікті, сонымен бірге оны тек
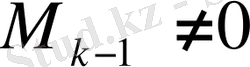 миноры бар минорлар арасынан іздеу қажет.
миноры бар минорлар арасынан іздеу қажет.
Мысал: матрица рангін табу
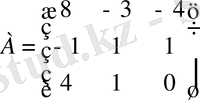 .
.
Шешуі.
Элементар тұрлендіру жолымен А
матрицасын
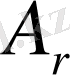 канондық түрге келтіреміз. Бірінші баған элементтеріне үшіншінің элементтерін қоса отырып, ал үшіншінің элементтерінен сәйкесінше екінші баған элементтерін азайтып, алатынымыз
канондық түрге келтіреміз. Бірінші баған элементтеріне үшіншінің элементтерін қоса отырып, ал үшіншінің элементтерінен сәйкесінше екінші баған элементтерін азайтып, алатынымыз
А
~
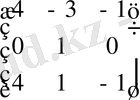 .
.
Бірінші баған элементтерін
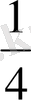 -ге көбейтеміз, сосын үшінші жол элементтерінен сәйкесінше бірінші жол элементтерін азайтамыз:
-ге көбейтеміз, сосын үшінші жол элементтерінен сәйкесінше бірінші жол элементтерін азайтамыз:
А
~
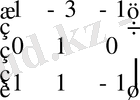 ~
~
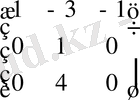 .
.
Үшінші жол элементтерінен 4-ке көбейтілген екіншінің элементтерін азайтамыз, ал сосын екінші және үшінші бағандар элементтерін сәйкесінше 3 және 1-ге көбейтілген бірінші баған элементтеріне қосамыз:
А
~
 ~
~
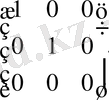 .
.
Осылайша, А матрицасының рангі 2-ге тең .
Мысал: Жиектелген минорлар әдісімен матрица рангін табу.
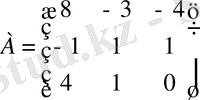 .
.
Шешуі .
Бірінші ретті
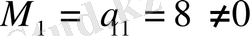 минорды қарастырамыз, осылайша, матрица рангі
минорды қарастырамыз, осылайша, матрица рангі
 .
.
Әрі қарай екінші ретті минорды қарастырамыз:
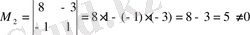 , нөлден өзгеше екінші ретті минор, онда
, нөлден өзгеше екінші ретті минор, онда
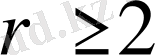 . Үшінші ретті минор мәнін табамыз:
. Үшінші ретті минор мәнін табамыз:
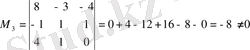 , сонымен, үшінші ретті минор 3-ке тең, яғни
, сонымен, үшінші ретті минор 3-ке тең, яғни

 .
.
Көрнекі материалдар
Слайдтар:
Слайд 1. Матрица анықтамасы.
Слайд 2. Матрица түрлері.
Слайд 3. Матрицаға қолданылатын амалдар.
Слайд 4. Матрица минорын анықтау.
Слайд 5. Матрицаның алгебралық толықтауышын анықтау.
Слайд 6. Матрица рангі.
Слайд 1. Матрица анықтамасы.
Анықтама:
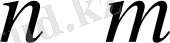 өлшемді матрица деп т жолдардан және п бағандардан құралған төртбұрышты сандар кестесінайтады. Матрицаны құрастыратын сандар матрица элементтері деп апталады.
өлшемді матрица деп т жолдардан және п бағандардан құралған төртбұрышты сандар кестесінайтады. Матрицаны құрастыратын сандар матрица элементтері деп апталады.
Матрица латын алфавитінің бас әрпімен белгіленеді, мысалы
А, В, С, …,
ал матрица элементтерін белгілеу үшін екі индексті кіші әріптер қолданылады:
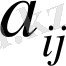 , мұндағы
, мұндағы
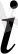 - жол нөмері,
- жол нөмері,
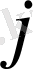 -баған нөмері. Матрица элементтері дөңгелек (кейде тік) жақшаға алынады.
-баған нөмері. Матрица элементтері дөңгелек (кейде тік) жақшаға алынады.
Мысал:

Қысқаша
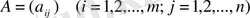 матрицасы түрінде белгіленеді.
матрицасы түрінде белгіленеді.
Мысал:

Слайд 2. Матрица түрлері.
Анықтама: бір жолдан тұратын матрица, жол-матрица (жол-вектор), ал бір бағаннан - баған-матрица (баған-вектор) деп аталады.
 - жол-матрица,
- жол-матрица,
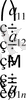 - баған-матрица.
- баған-матрица.
Мысал:
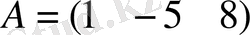 - жол-матрица,
- жол-матрица,
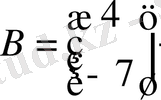 -баған матрица.
-баған матрица.
Анықтама: Егер матрица жолдарының саны баған сандарына тең болса, онда матрицаны квадраттық матрица деп атайды.
Мысал
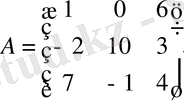 -
3-ші ретті квадраттық матрица.
-
3-ші ретті квадраттық матрица.
Анықтама: Егер матрицаның жол мен баған сандары сәйкеспесе, онда матрица тікбұрышты деп атайды.
Мыал:
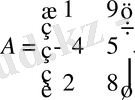 -
-
 өлшемді тікбұрышты матрица.
өлшемді тікбұрышты матрица.
Анықтама:
Жол және баған нөмерлері сәйкес болатын матрица элементтері бас диагоналды құрайды және диагоналды деп аталады. Квадраттық матрица үшін басдиагонал элементтері
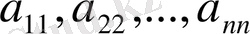 құрайды.
құрайды.
Анықтама: Егер квадрат матрицаның барлық диагональ емес элементтері нөлге тең болса, онда матрица диагональды деп аталады, яғни:
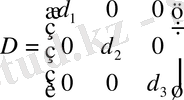
Мысал:
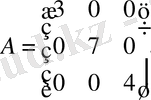 -
3-ші реті диагональды матрица.
-
3-ші реті диагональды матрица.
Анықтама: Егер диагональды матрицаның барлық диагональды элементтері бірге тең болса, онда матрица бірлік матрица деп аталады және и Е әрпімен белгіленеді.
Мысал:
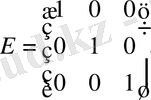 -
3-ші ретті бірлік матрица.
-
3-ші ретті бірлік матрица.
Анықтама: Кез келген өлшемді матрица нөлдік немесе нөл-матрица деп аталады, егер оның барлық элементтері нөлге тең болса.
 .
.
Анықтама : Бас диагоналы нөл болатын квадраттық матрица үшбұрышты матрица деп аталады.
Мысал:
 -
3-ші ретті үшбұрышты матрица.
-
3-ші ретті үшбұрышты матрица.
Анықтама : Матрицалар тең деп аталады, егер олардың жол және баған сандары бірдей болып және сәйкес орындарда тең сандар тұрса.
Слайд 3. Матрицаға қолданылатын амалдар
1. Матрицаны санға көбейту
Анықтама:
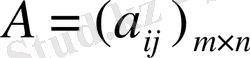 матрицасының
матрицасының
 санына көбейтіндісі деп
санына көбейтіндісі деп
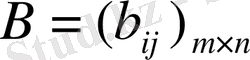 матрицасының әрбір элементтері,
матрицасының әрбір элементтері,
 санын
санын
 матрицасының сәйкес элементтерінің көбейтіндісіне тең матрицаны айтады:
матрицасының сәйкес элементтерінің көбейтіндісіне тең матрицаны айтады:
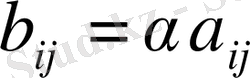 ,
,
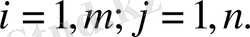
Мысал:
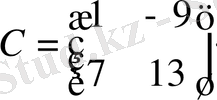 ,
,
 .
:
.
:
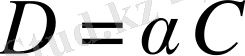 матрицасын табу.
матрицасын табу.
Шешуі :
 .
.
Салдар: Матрицаның барлық элементтерінің ортақ бөлгішін матрица белгісінің алдына шығаруға болады.
Мысал:
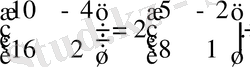
Салдар:
Матрицаның 0 санына көбейтіндісі нөлдік матрица.
2. Матрицалардың қосындысы
Анықтама: А және В бірдей өлшемді екі матрицаның қосындысы деп, А және В матрицалардың әрбір элементі сәйкес элементтердің қосындысына(айырмасын) тең болатын С=А+В матрицасын айтады:
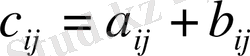 , где:
, где:
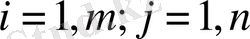
( яғни. матрицалар элементтері бойынша қойылады) .
Мысалы:
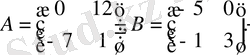 Онда:
Онда:
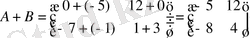 .
.
3. Матрицалар айырмасы
Бірдейөлшемді екі матрицаның айырмасы алдындағы амал арқылы анықталады:
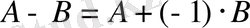 .
.
Слайд 4.
Анықтама:
п-ші ретті
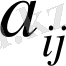 матрица элементінің
матрица элементінің
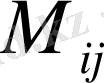 минорлары деп
минорлары деп
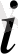 -ші жолдар және
-ші жолдар және
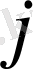 -ші бағандарын сызып тастағаннан кейін А матрицасынан алынған
-ші бағандарын сызып тастағаннан кейін А матрицасынан алынған
 -ші ретті матрица анықтауышын айтады.
-ші ретті матрица анықтауышын айтады.
Мысалы: 3х3 матрицасы берілген:
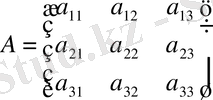 .
.
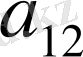 матрицы А үшінші ретті матрицаның
матрицы А үшінші ретті матрицаның
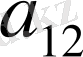 элементінің миноры:
элементінің миноры:
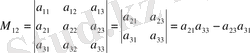 .
.
Слайд 5.
Анықтама:
п-ші ретті матрицаның
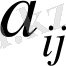 элементінің
элементінің
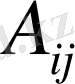 алгебралық толықтауышы деп,
алгебралық толықтауышы деп,
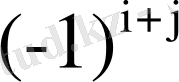 :
:
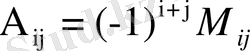 белгісімен алынған оның минорын айтады.
белгісімен алынған оның минорын айтады.
Мысал:
Алдынғы мыалдан
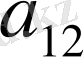 элементінің алгебралық толықтауышы мына түрде болады:
элементінің алгебралық толықтауышы мына түрде болады:
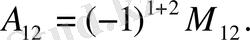
Мысал: Матрица берілген:
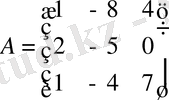 .
.
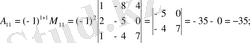
Слайд 6
Анықтама: Матрицаның нолге тең емес минорларының ең үлкен реті матрица рангісі деп аталады: r=r(A) = rangA .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz