Бөлшектердің толқындық қасиеттерінің гипотезасы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

№ 14 дәріс тақырыбы: Электрмагниттік сәуле шығарудың кванттық табиғаты

Негізгі сұрақтар:

Абсолют қара дененің сәуле шығаруының мәселелері.
Кванттық гипотеза және Планк формуласы.
Фотондар. Фотоэффект. Комптон эффектісі.
Электрмагниттік сәуле шығарудың корпускулалық толқындық дуализміфотонның массасы және импульсі қалай анықталады?
Комптон эффектісін түсіндір.
Комптондық толқын ұзындығы қалай анықталады?
Заттың корпускулалық толқындық дуализмі.
Де Бройльдің гипотезасы.
Микробөлшектердің толқындық қасиеттері және Гейзенбергтің анықталмағандықтар қатысы.
Анықталмағандықтар қатысы кванттық механиканың іргелі принципі.
Анықталмағандық қатынасқа анықтама бер.
Анықталмағандық қатынасты ашқан ғалым кім?

Фотоэлектрлі эффект. Сыртқы фотоэффект заңдары

Фотоэлектрлі эффект немесе фотоэффект деп белгілі бір толқын ұзындықтағы түсірілген жарықтың әсерінен металдардың электрондарды шығару құбылысын айтады. Металдардағы эффект сыртқы фотоэффект деп аталады, өйткені бұл жағдайда электрондар металдардан сыртқы қоршаған ортаға, яғни вакуумға шығады.

Сыртқы фотоэффект құбылысын 1888 жылы А. Г. Столетов ашқан болатын. Металдардан ұшып шығатын электрондардың жылдамдығы түскен жарықтың қарқындылығына емес, оның жиілігін тәуелді. Фотоэффектің бұл заңдылығы жарықтың толқындық теориясы тұрғысынан айқындалмаған болып шықты. Жарықтың қарқындылығы үлкен болған сайын (жарықтың толқындық энергиясы) ұшып шығатын электрондардың жылдамдығы да үлкен болуы керек еді.

Фотоэффекттің бұл негізгі заңдылығын 1905 жылы Эйнштейн жарықтың сәулеленуінің кванттық сипаты тұрғысынан алып түсіндірген. Абсолютті қара дененің кванттық сипаты сияқты, Эйнштейн фотоэфффект кезінде металға жарық кванттары (фотондар)

\[e=h\nu\]

(19. 1)

энергиясымен түседі деп болжады, мұнда

\[{}^{\prime}{\mathfrak{p}}\]

-түскен жарық жиілігі, ал h = 6. 62·10 ^-27 эрг· с = 6. 62·10 ^-34 Дж·с- Планк тұрақтысы.

Эйнштейн бойынша, энергияның сақталу заңымен кванттың бұл энергиясы электронның

\[\textstyle A_{\phi}\]

металдан шығу жұмысынын жеңуге және ұшып шығатын электронға белгілі бір энергия беруге шығындалады:

\[h n=A_{\phi}+\frac{m\vartheta_{m}^{2}}{2}\]

(19. 2)

мұнда m - электрон массасы, ал

\[{\mathcal{Q}}_{m}\]

-оның максимал жылдамдығы

(19. 2) теңдігі фотоэффект құбылысына қолданылған энергияның сақталу заңы, ол фотоэффект теңдеуі деп аталады.

Фотоэффект теңдеуінен электронның жылдамдығы тек түскен жарықтың жиілігіне байланысты екендігі көрінеді. Сондай-ақ (19. 2) -тен фотоэффекттің максимал кинетикалық энергиясы , максимал жылдамдығы және фотоэффектінің қызыл шекарасы анықталады. Шынында да, егер квант энергиясы шығу жұмысын жеңуге жеткілікті болса фотоэффект әбден болуы мүмкін. Бұл кезде минималь жиілік

\[h\nu_{\mathrm{\tiny~min}}=A_{\phi}\]

(19. 3)

немесе

\[\nu_{\mathrm{\scriptsize~min}}=\frac{A_{\phi}}{h}\]

(19. 4)

теңдіктерінен анықталады, осы минималь жиілікке

\[\lambda_{m}\,\]

толқынының минимал ұзындығы сәйкес келеді

\[l_{\mathit{m}}={\frac{c}{\nu_{\mathit{m i n}}}}={\frac{c h}{A_{\phi}}}\]

(19. 5)

(19. 5) теңдеуі электронның шығу жұмысы бойынша берілген металл үшін фотоэффекттің болу мүмкіндігін анықтайтын максимал ұзындықты толқынды анықтайды.

Сыртқы фотоэффект қолданылатын ең қарапайым құрал - фотоэлемент- екі металл электроды - катод пен аноды бар шыны баллон. Баллон ішіндегі ауа сорылып алынып, электрондар фотокатодтан анодқа еркін жетуі үшін өте жоғары вакуум жасалған. Фотоэлементтің фотокатоды ретінде баллон шынысының металдық ішкі қабаты алынады. Фотоэлемент аноды темір сым тұзақ алынады. Ол фотоэлементке түсетін барлық жарық ағынын өткізу керек. Егер фотоэлементті нақты бір толқын ұзындықты жарықпен жарықтандырып

\[(l\ \simeq\lambda_{m})\]

, ал электродтарды тұрақты U кернеуге қосса, онда тізбекке қосылған микроамперметр онда тоқтың бар екендігін көрсетеді. Басқа сөзбен айтқанда, осындай фотоэлементті қолданып сыртқы фотоэффекті зерттеп бақылауға болады.

Фотонның импулсі және энергиясы

Фотоэффектіні жарықтың жұтылуының кванттық сипатымен түсіндіре отырып, Эйнштейн жалпы гипотеза ұсынды: жарық ерекше жарық бөлшектері - жарық кванттары (фотондар) түрінде таралады. Жарық бір жағынан, электромагниттік толқындар болып табылады, ал екінші жағынан - ол бөлшектер жиынтығына тән бірқатар қасиеттерге ие. Осының өзі жарықтың электромагниттік өрісін элементар бөлшектердің жиынтығы - фотондар деп қарастыруға мүмкіндік береді. Фотондар белгілі бір энергияға, массаға, импульске және спинге ие. Фотондар бөлшектер ретінде

\[c=3\cdot10^{8}\,i\ \prime\,\tilde{n}\]

жылдамдықпен қозғалса, оларға релятивтік механика қолданылады және фотонның массасы мынаған тең болады (Эйнштейннің формуласы бойынша

\[\mathrm{E}=m c^{2}\]

)

\[m_{\phi}=\frac{e}{c^{2}}=\frac{h\nu}{c^{2}}\]

, (19. 6)

ал оның импульсы (

\[\varepsilon^{2}\,/c^{2}={\sqrt{p^{2}+m_{0}^{2}\cdot c^{2}}}\]

формуласы бойынша)

\[p={\frac{e}{c}}={\frac{h\nu}{c}}\]

. (19. 7)

Фотон тек 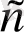жылдамдықпен қозғалатын бөлшек, оның тыныштық массасы нөлге тең (

\[m_{0}=0\]

) және бұдан оның ерекше бөлшектер тегіне жататындығы көрінеді.

Егер фотоэлементтің электродына түсірілетін

\[{\boldsymbol{U}}\]

кернеуді өзгертетін болса, онда тізбектегі

\[\mathbf{I}_{\delta}\]

фототок күші де өзгереді. Жарық ағыны өзгермейтін жағдайда фототоктың фотоэлементке берілген кернеуге тәуелділігі фотоэлементтің вольтамперлік сипаттамасы делінеді. Фотоэлементтің вольтамперлік мінездемесі графигінен көрінгендей, түсірілген нөлдік кернеуде (

\[{\boldsymbol{U}}\]

=0) фототок нөлге тең емес және қандайда бір теріс

\[U_{\alpha}\]

“жабушы” кернеуде толығымен тоқталады. ¤з кезегінде, қандай да бір оң

\[U_{\mathrm{0}}\]

кернеуде қанығу басталады, бұл жағдайда тоқ күші кернеудің оң артуымен қатар артпайды. Сондай-ақ, 93-суретте көрсетілгендей кернеудің

\[U_{\alpha}\]

-ден

\[U_{\mathrm{0}}\]

-ге дейінгі аралығында фототоктың кернеуге пропорционал өсуі сәйкес келеді.

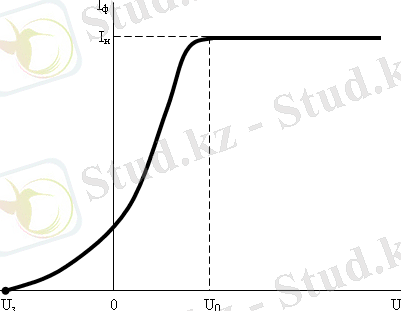
93-суретте

Қанығу тоғының бар болуы катодтан ұшып шығатын барлық фотоэлектрондардың анодқа келіп жететіндігін көрсетеді. Екіншіден, анодтағы нөлдік кернеуде фототоғының нөлге тең болмауы, фотоэлектрондардың фотокатодтан белгілі кинетикалық энергиямен және белгілі жылдамдықпен ұшып шығатынын көрсетеді. ¦шып шыққан электрондардың максималды жылдамдығын мынадай шарттан анықтауға болады: ток

\[U_{\alpha}\]

жабушы кернеуде тоқталады (фотоэлемент бекітіледі), яғни

\[\frac{m\vartheta_{m}^{2}}{2}=e U_{\alpha}\]

(19. 8)

-электронның заряды, ал-электронның максимал жылдамдығы.

(19. 8) теңдігін қолданып,
\[\boldsymbol{U_{\alpha}}\]
кернеудегі фотоэлектрондардың максимал жылдамдығын анықтауға болады

\[\delta_{m}=\sqrt{\frac{2e}{m}}{U}_{\alpha}\]

(19. 9)

Комптон эффектісі

Рентгендік сәулеленудің электромагниттік сәулеленудің бір түрі екендігін 1895 жылы сиретілген газдардағы электр разрядтарын зерттеу кезінде Рентген ашты. Металды электродтарда (анодта) электрондардың тежелуі кезінде сәулелену пайда болады. Сондықтан оны спектрі тұтас болып келетін тежеуші рентгендік сәулелену деп атаған. Кейінірек, атомдық физиканың дамуымен қатар сызықтық спектрлі сипатта сипаттамалық рентгендік сәулелену зерттеле бастады.

1923 жылы қатты денелерен рентгендік сәулелердің шашырауын зерттей отырып, Комптон шашыраған сәулелерде арасында ұзындығы

\[\mathcal{M}\]

алғашқы сәулелермен қатар

\[\ \lambda^{'}\]

ұзын толқындық компонентасының бар екендігін анықтады.

\[\mathbf{M}=l^{1}{\boldsymbol{\ldots}}\]

толқын ұзындықтарының айырымы шашыратушы материалдарға тәуелді емес және алғашқы және шашырау бағыттар арасындағы

\[\hat{U}\]

бұрышының функциясы екендігі анықталды. Тәжірибе нәтижесінде келесідей заңдылық орнатылады

\[\mathrm{D}I=c o n s t(1-\cos\theta)\]

немесе

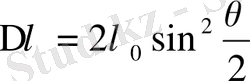(19. 10)

мұндағы тұрақты шама

\[\lambda_{0}=0.0242{\mathrm{A}}^{0}\]

-ге тең.

Комптон тәжірибесінің нәтиже кванттық теория негізінде түсіндіріледі. Рентгендік сәулелену сәулеленудің кванттық ағыны (рентгендік фотондар) ретінде қарастырылды, сондай кванттар энергия мен және салмаққа ғана емес, сонымен қатар импульске ие болуы керек делінді.

Комптон формуласынын теориялық қорытуда рентгендік фотондар бөлшектер сияқты шашыратушы заттардың бос электрондарымен серпімді соқтығысқан кезде энергияның сақталу заңымен қатар импульстің сақталу заңы да орындалады деп қарастырылды. .

Сонымен, энергиясы

\[\varepsilon=h\nu\]

рентгендік квант бастапқы кезде тыныштықтағы бос электронмен серпімді соқтығысады деп жорамалдайық. Релятивистік механиканың формуласын ескере отырып энергияны сақталу заңы мына түрде жазылады

\[h\nu+m_{0}c^{2}=h\nu\,^{*}+m c^{2}\]

(19. 11)

Осы сияқты импульстің сақталу заңын жазуға болады

\[{\frac{h\nu}{c}}{\frac{\Gamma}{n_{1}}}={m\nu}+{\frac{h\nu^{*}}{c}}\frac{\Gamma}{n_{2}}\]

(19. 12)

мұндағы

\[{\mathcal{N}}_{\parallel}\]

мен

\[{\mathfrak{n}}_{2}\]

-алғашқы және шашыраған шоқтарға бағытталған бірлік вектор;

\[{\mathfrak{m}}\]

және

\[{\boldsymbol{\sqrt{f\ }}}\]

-электронның массасы мен жылдамдығы;

\[m_{0}\]

-электронның тыныштық массасы;

\[{\partial^{\dagger}}\]

-шашыраушы рентгендік кванттың жиілігі

\[\begin{array}{r c l}{{\oplus_{1}^{\prime}\cdot=\frac{c\odot}{\lambda^{\prime}}\oint_{0}^{\prime}}}\end{array}\]

. Егер (19. 11) теңдігін

\[\frac{\xi}{J_{I}}\]

-ға бөлсе, онда

\[m c=m_{0}c+{\frac{\bar{\bf c}}{\bar{\bf c}}}{\frac{h J}{c}}-{\frac{h\vartheta^{'}}{c}}{\frac{\bar{\bf c}}{\Lambda}}\]

(19. 13)

және (19. 13) -ті квадраттағанда

\[m^{2}c^{2}=m_{0}^{2}c^{2}+{\frac{\alpha\bar{b}J}{\bar{c}\cdot\frac{\bar{\Theta}}{c}\cdot\frac{\bar{\Theta}}{\bar{\phi}}}}\cdot{\frac{\bar{\Theta}}{\bar{c}\cdot\frac{\bar{c}}{\bar{\phi}}}}\cdot2\frac{\alpha\bar{\phi}\bar{b}J^{'}\frac{\bar{\phi}}{\bar{\phi}}}{c\cdot\frac{\bar{\phi}}{\bar{\phi}}}\cdot\frac{\bar{\phi}}{c\cdot\frac{\bar{\phi}}{\bar{\phi}}}-\frac{\bar{b}}{c}\frac{\bar{\phi}}{c}\]

(19. 14)

(19. 12) теңдіктің екі жағын да квадраттаса

\[m^{2}J^{2}=_{\hat{\underline{{{\hat{\alpha}}}}}}^{\alpha\hat{L}J}\ {\stackrel{\partial^{2}}{\hat{\hat{\alpha}}}}^{\underline{{{\alpha}}}}\ +_{\hat{\hat{\hat{Q}}}}^{\underline{{{\alpha}}}\hat{L}J}\ {\stackrel{\hat{\hat{\alpha}}}{\hat{\hat{\alpha}}}}^{2}\ \sim\ 2_{\hat{\hat{\hat{\alpha}}}}^{\alpha\hat{L}J}\ c\ {\frac{\hat{\hat{\alpha}}}{\hat{\hat{\alpha}}}}^{\hat{\hat{\alpha}}}\propto\delta\theta\]

(19. 15)

өйткені, бірлік вектордың скаляр көбейтіндісі

\[(^{i}n_{1}{}^{i}_{2})=\cos\theta\]

(19. 14) теңдіктен (19. 15) -ні алса мынай теңдік шығады

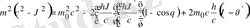(19. 16)

Электронның

\[m={\frac{m_{0}}{\sqrt{1-\ 9^{\ 2}/c^{2}}}}\]

массасын ескерген жағдайда

\[m^{2}(c^{2}-\vartheta^{2})\!=\!m_{0}^{2}c^{2}\]

, сонда (19. 16) теңдігі мына түрде жазылады

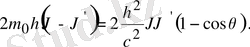(19. 17)

(19. 17) теңдіктің екі жағын да

\[J\,\phi^{\prime}\]

көбейтіндісіне бөліп және

\[\frac{\bar{n}}{J}=l\;,\;\frac{\bar{n}}{J\,\phi}\!=\!\lambda^{\prime}\]

екендігін ескеріп, төмендегідей өрнек жазуға болады

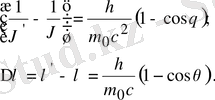(19. 18)

(19. 18) формуласы тәжірибелік мәнге сәйкес келеді, ал

\[{\bar{A}}_{0}\]

тұрақтысы мынаған тең

\[\lambda_{0}={\frac{h}{m_{0}c}}.\]

(19. 19)

\[\lambda_{0}\]

үшін формуланы тағы мына түрде жазуға болады

\[l_{{\bf\ 0}}=2p\,\frac{h}{2p m_{0}c}=2\pi\Lambda,\]

(19. 20)

мұндағы

\[\Lambda\]

- өлшемі толқын ұзындығының өлшеміндей шама, ол мынаған тең

\[\mathrm{L}={\frac{h}{2m_{0}c}},\]

(19. 21)

мұны комптондық толқын ұзындығы деп атайды.

\[m_{0},h,c\]

тұрақтыларының мәндерін қойып,

\[\Lambda\]

сан мәнін анықтауға болады

\[\mathbf{L}=0.00386{\dot{\mathbf{A}}}\]

(19. 22)

Комптон формуласынан шығатындай, ал тәжірибе нәтижелері дәлелдегендей, заттан рентген сәулелері шашырағанда электрондар ағыны пайда болады.

Сонымен, Комптон эффектісі сәулеленудің кванттық теорияның тәжірибелік дәлелдемесі болады. Сонымен қатар, сәулелену кванттарының (рентгендік фотондар) белгілі бір импульске ие екендігі анықталды. .

Бөлшектердің толқындық қасиеттерінің гипотезасы. Толқындық функция және оның физикалық мағынасы. Корпускулалық -толқындық дуализм. Микробөлшектердің кванттық күйі. Кванттық қозғалыс теңдеулері

ХХ ғасырдың басында физиканың дамуы классикалық механиканы микробөлшектерге, сонымен қоса атомдарға және оның оның құрамды бөлшектеріне қолдануға келмейтінін көрсетті. Сондықтан ХХ ғасырдың 20-жылдарында біріншіден, электронға және басқа қарапайым бөлшектерге қолданылатын кванттық (толқындық) механика пайда болды. Кванттық механиканың пайда болуы классикалық статистиканың пайда болуына әкеп тіреді: электрон және басқа да микробөлшектер үшін Максвелл-Больцманның кванттық статистикасын Ферми-Дирак статистикасына алмастыру қажеттігін көрсетті.

Алдымен сәулеленудің корпускулярлық қасиетін қарастырамыз. Абсолютік қара дененің жылулық сәулеленуі мен фотоэффектіні теориялық зерттеулер кезінде сәулені шығару мен жұтулар жеке-жеке порциялар (квант) түрінде өтетіндігі, жарықтың квант энергиясы

\[e=h\partial\]

екендігі тағайындалды, немесе басқаша жазғанда

\[e={\mathrm{Im}}\]

(21. 1)

мұндағы

\[w=2\pi\vartheta\]

- бұрыштық жиілік; ал

\[\textstyle{\uparrow={\frac{h}{2\pi}}}\]

-Планк тұрақтысы.

Жарық кванты немесе фотон, тыныштық массасы жоқ ерекше бөлшектер (корпускулалар) энергияға, импульске (қозғалыс мөлшеріне) ие

\[p={\frac{e}{c}}={\frac{\mathrm{li}\omega}{c}}\]

(21. 2)

массасы

\[m_{o}={\frac{e}{c^{2}}}={\frac{\mathrm{I}\omega}{c^{2}}}\]

(21. 3)

мұндағы с - вакуумдегі жарық жылдамдығы.

Сонымен, жарық (сәулелену) толқындық қасиетімен қатар корпускулярлық қасиетке де ие.

Жарықтың толқындық және кванттық теорияларының өзара үйлесуін қарастырайық. Оптикадан белгілі, жарықтың толқындық теориясына байланысты кеңістіктің берілген нүктесіндегі толқынның қарқындылығы оның амплитудасының квадратына пропорционал. Ал жарықтың кванттық теориясы бойынша кеңістіктің берілген нүктесіндегі жарықтың қарқындылығы осы кеңістікке түсетін фотондар санына пропорционал. Сонымен теориялар үйлесімі мынадай: кеңістікке түскен фотондар саны кеңістіктің берілген нүктесіндегі толқын амплитудасының квадратына пропорционал, яғни олар бір-бірімен пропорционал байланысқан деп ұйғарылады.

Қарапайым бөлшектердің толқындық қасиеттерін қарастырайық. Алғаш рет 1925 ж. француз физигі де Бройль электрондардың толқындық қасиеттері жөнінде ғылыми болжам жасаған. Де Бройльдың негізгі идеясы квант теориясының негізгі қатынастарын қозғалыстағы элементар бөлшектер қозғалысына қолдану болды.

Сонымен, ол импульсі

\[\frac{\Gamma}{p}=m{\dot{\theta}}^{\frac{1}{2}}\]

және кинетикалық энергиясы

\[E_{k}\]

еркін электрон жазық толқын түрінде сипатталуы керектігін болжамдады.

\[\displaystyle{\bf Y=}_{0}\!e^{\frac{i\Omega E_{k}t}{6}-\frac{1}{P}\!\!\!\!\stackrel{\cdot I}{\|}{\phi}_{,}}\]

(21. 4)

мұндағы скалярлық көбейтінді

\[\stackrel{1}{P T}\]

мынаған тең:

\[{\stackrel{1}{p}}\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\]

(21. 5)

ал,

\[{\boldsymbol{\varphi}}_{0}\]

- тұрақты амплитуда.

Де Бройль жарықтың кванттық теориясына сәйкес фотонның энергиясы мен импульсін анықтайтын (21. 1) және (21. 2) формулалар еркін электрондарды толқын ретінде қарастырғанда орындалады деп жорамалдады, яғни осындай толқынның

\[({\mathcal{I}})\]

жиілігі және толқындық сан k төмендегідей формулалармен анықталады:

\[\omega={\frac{E_{k}}{\ln}}\,,\]

(21. 6)

\[k={\frac{2p}{\lambda}}={\frac{p}{\ln}}.\]

(21. 7)

Жазық электромагниттік толқын теңдеуін

\[y~=\psi_{\,0}e^{i\left(\omega t-k r\right)}\]

(21. 6) және (21. 7) -ші формулалардың көмегімен мына түрде жазуға болады

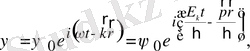
яғни, де Бройль толқыны деп аталған жазық толқынды аламыз.

Қарапайым түрде ОХ осінің бойымен қозғалатын еркін электрон қозғалысының толқындық функциясы

\[y\ (x,t)\!=\!\psi_{0}e^{\frac{i c E_{k}t}{\P}-\frac{p_{x}x{\dim}}{\ln}}\]

(21. 8)

1927 ж. электрондардың дифракциясы бойынша тәжірибелерде де Бройльдың ғылыми болжамы дәлелденді, кейінірек басқа элементар бөлшектердің толқындық қасиеттері анықталды. Сондықтан,

\[{\boldsymbol{\sqrt{f\ }}}\]

жылдамдықпен немесе р импульспен қозғалатын электронға ұзындығы

\[\mathcal{M}\]

толқын сәйкес келеді

\[l={\frac{2p{\bf\dot{p}}}{p}}=h/m\theta\,.\]

(21. 9)

бұл де Бройльдың толқын ұзындығы деп аталады.

Жарықтың кванттық және толқындық теорияларының үйлесімділігінен элементар бөлшектердің, соның ішінде электронның корпускулярлық және толқындық қасиеттерінің үйлесімділігін алуға болады. Бұл жағдайда берілген элементар

\[d V\]

көлеміне түсетін электрондар (элементар бөлшектер) саны де Бройль толқынының амплитудасының квадратына немесе оның модулінің квадратына пропорционал деп болжам жасауға тура келеді, демек электрондар саны мөлшермен

\[\varphi_{0}^{\ 2}d V\]

-ға тең.

Егер соңғы формуланы статистикалық тұрғыдан бір элементар бөлшек үшін қарастырғанда, берілген

\[d V\]

элементар көлемде осы бөлшектің табылу ықтималдығы де Бройль толқынының амплитудасының квадратына немесе осы толқынның модулінің квадратына пропорционал, яғни

\[d W=\mid y\mid^{2}d V=\psi\psi\quad*d V.\]

(21. 10)

Бұл теңдіктен де Бройль толқыны модулінің квадраты кеңістіктің берілген жерінде еркін бөлшектердің табылу ықтималдығының тығыздығына тең екендігі анықталады. Толқын функциясының мұндай түсіндірмесі тек еркін электрондар үшін ғана емес, сонымен бірге еріксіз электрондар үшін де дұрыс.

Сондықтан, толқындық функцияның физикалық мағынасы мынада: оның модулінің квадраты кеңістіктің берілген жеріндегі элементар бөлшектердің (электрондардың) ықтималдылық тығыздығын анықтайды. Сондай-ақ толқындық функция комплексті шама болып табылады. Монохроматты толқындарды немесе толқындар тобын (пакет) қарастыратын болса

\[\psi\left(x,t\right)=\sum_{k_{0}}^{k_{0}+\Delta k}c(k)e^{i\left(\omega t-k x\right)}d k\]

(мұндағы

\[k_{0}\]

- топтың ортасына сәйкес келетін толқындық сан) қарастырсақ, онда топтық жылдамдық

\[{\mathcal{Y}}_{\partial}\]

немесе толқын тобының жылдамдығы

\[{\bar{\mathcal{M}}}\]

төмендегі формуламен анықталады:

\[\quad J_{\bar{a}\bar{o}}=\dot{e}={\frac{d\omega}{d k}}.\]

Екінші жағынан, (21. 6) және (21. 7) еркін электрон үшін

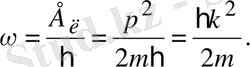
Онда соңғы формула негізінде толқын тобының жылдамдығы немесе пакет жылдамдығы мынған тең

\[u=\frac{d}{d k}\frac{\hat{\mathrm{e}}_{\parallel}k^{2}\,\mathrm{l}}{\hat{\mathrm{e}}^{2m}\,\hat{\mathrm{e}}^{2}}\frac{\mathrm{l}k}{\mathrm{l}}=\hat{\mathrm{-}}\theta\]

мұндағы

\[{\underline{{\psi}}}{\overline{{f}}}\]

- еркін электронның лездік жылдамдығы.

Сөйтіп, де Бройльдың толқынының топтық жылдамдығы электронның (элементар бөлшектердік) қозғалыс жылдамдығына тең. Еркін электрондардың толқындық функцияны немесе де Бройль толқыны көрнекі физикалық анықтамаға ие: еркін электрондардың қозғалысын де Бройльдың толқындары (пакет) тобының қозғалысы ретінде қарастыруға болады.

Атомдар мен молеклалардың энергиялық спектрі

XIX ғасырдың соңғы он жылдықтарында атомдарға сызықтық спектрлер , ал молекулаларға жолақты спектрлер тән екендігі нақты анықталады. Атомның сызықтық спектрлері анығырақ болып келеді, олар сызықтар жиынтығынан (сериялардан) тұрады. Ең қарапайым атом - сутегі атомының спектрі жақсы зерттелген: оптикалық спектрлердің көрінетін бөлігінде - Бальмер сериясы; ультракүлгін бөлігінде - Лайман сериясы; ал алыс инфрақызыл аумағында Пашен, Брэкет және Пфунд сериялары.

Спектрдің көрінетін бөлігіндегі спектрлік серияның толқын ұзындығын есептеуге Бальмер мына формуланы ұсынды:

\[l\,=\lambda_{0}\,\frac{n^{2}}{n^{2}-4},\]

(21. 11)

мұңдағы λ ₀ -ұзындық өлшемді тұрақты, ал n - бүтін сан, мына мәндерге n= 3, 4, 5 . . . тең.

Бірақ та спектроскопияда спектрлік сызықтарды толқындық сандар немесе толқын ұзындықтарына кері шамамен сипатталу ұсынылған:

\[n^{\,y}={\frac{1}{\lambda}}.\]

(21. 12)

Толқындық сандар арқылы жазылған (21. 11) Бальмер формуласын мына түрге келтіруге болады:

\[\nu^{'}=R_{\tilde{\underline{{{\mathrm{G}}}}}\,\underline{{{1}}}^{2}}-{\frac{1}{n^{2}\,\frac{\tilde{\vartheta}}{\vartheta}}}\quad n=3,4,5,\dots,\]

(21. 13)

мұндағы тұрақты шама

\[R=109737.3\,{\tilde{n}}i\]

(21. 14)

Ридберг тұрақтысы деп аталады.

Кейінірек сутегі атомындағы басқа да барлық спектрлік сериялардың толқындық сандарын Бальмердің жалпылама формуласы арқылы есептеуге болатындығы тағайындалды:

\[\nu\,={\cal R}_{\underline{{{\mathrm{C}}}}}^{\underline{{{\alpha}}}}{\!\underline{{{\mathrm{\tiny~1}}}}}^{}-\frac{1}{n^{2}}^{\hat{\mathrm{2}}}\hat{\phi}\]

(21. 15)

мұнда Бальмер сериясы үшін m бүтін сан 2 деген мәнге ие болады; 1- Лайман сериясы үшін; 3 - Пашен сериясы үшін және басқа сериялар үшін m = 4, 5, 6 . . . Мұндағы әр сериядағы n санының бүтін мәні сол серия үшін (m+ 1) мәнінен басталады.

\[{\boldsymbol{\psi}}^{\prime}\]

спектрлік толқындық сан ω бұрыштық жиілік пен с жарық жылдамдығына жай қатынаспен байланысты:

\[n^{\ '}={\frac{1}{l}}={\frac{f}{c}}={\frac{w}{2\pi c}},\]

(21. 16)

мұндағы f =

\[\frac{w}{2\pi}\]

циклдік жиілік, осы арқылы (21. 15) жалпы формуланы басқа түрде жазуға болады:

\[\omega={R}{\frac{\mathrm{vx}\ 1}{\bar{\mathrm{g}}m^{2}}}-{\frac{1}{n^{2}}}{\frac{\mathrm{d}}{\phi}}\]

(21. 17)

мұндағы R Ридберг тұрақтысына пропорционал тұрақты шама

\[R=2\pi c\cdot R\]

(21. 18)