Классикалық статистикадағы үлестірулер

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Лекция №11 Оқу тобы: 128-17а

Тақырыбы: Классикалық статистикадағы үлестірулер.

Микроканондық үлестіру. Канондық үлестіру. Гиббстің микроканондық үлестірімдігі. Канондық үлестіру параметрлерінің физикалық мағынасы
Термодинамикалық ықтималдық. Энтропия жəне оның күйлер ықтималдығымен байланысы. Максвелл-Больцман үлестіруі. Үлкен канондық үлестіру

Микроканондық үлестірімдік.

Статистикалық үлестірімдік функциясының формуласын анықтау үшін статистикалық физика аксиомасын пайдалану керек. Бұл аксиоманың салдары тәжірибе жүзінде дәлелденеді. Оны статистикалық физика постулаты деп атайды.

Бұл 2 тәсілмен қарастырылады:

Бірінші тәсілде энергиялары тең бірдей жүйелер ансамблі қарастырылады. Сол арқылы теңбе- тең өзара тәуелсіз тұйық жүйенің әртүрлі күйлерінің ықтималдықтары қарастырылады. Бұндай ансамбль микроканондық , ал үлестрімдік микроканондық деп аталады.

Екінші тәсілде теңбе тең күйде орналасқан тұйық жүйе квазитәуелсіз бөліктерінен құралған ансамбль деп зерттеледі. Ансамбль мүшелерінің энергиялары бірдей болмауы мүмкін, сол арқылы квазитәуелсіз жүйелердің әртүрлі энергияларға сәйкес келетін микрокүйлерінің ықтималдықтары қарастырылады. Бұндай ансамбль канондық және үлестрімдік канондық деп аталады.

Статистикалық физиканың микроканондық үлестрімдік жайында постулаты :

«Теңбе-тең тұйық жүйенің барлық микрокүйлерінің ықтималдықтары бірдей».

Жүйе өте үлкен уақыт аралықтарында барлық мүмкін микрокүйлерін өтеді делік, онда микроканондық үлестрімдік постулатына сәйкес әрбір микрокүйде жүйенің бөгелу (тұрақтау) уақыты орташа есеппен бірдей болады. Бұл микроканондық үлестрімдіктің ережесі, эргодикалық гипотезаға парапар.

Е ₀ Е

ρ(Е)

1-сурет. Микроканондық үлестірімділіктің графигі.

Классикалық физикада микроканондық үлестрімдікті математикалық формуламен көрсету үшін фазалық кеңістікте бір Е ₀ энергия мәніне сәйкес келетін жүйенің мүмкін күйлерін бейнелейтін фазалық нүктелердің геометриялық орнын қарастырайық.

Бұл фигура фазалық кеңістіктегіден өлшем саны біреуге кем кеңістік, яғни гипербет болады. Сонда осы фазалық бетте ықтималдықтың тығыздығы нөлге тең емес, басқа нүктелерде нөлге тең. Статистикалық үлестрімдік функциясы дегеніміз фазалық кеңістікте ықтималдықтың тығыздығы болып табылады. Сонымен:

; (7. 1)

мұндағы -Дирак функциясы. Бұл формула Гиббстің микроканондық үлестрімдігі деп аталады. Ол график түрінде 1-суретте көрсетілген.

Гиббстің микроканондық үлестірімділігі 1-тәсілге сәйкес келеді. 2-тәсілге сәйкес келетін үлестірімділік жүйе бөліктерінің энергия бойынша үлестрімдігін сипаттайды. Оны қорыту үшін энергиялардың аддитивтік қасиетін ескеру керек. Яғни жүйе энергиясының оның бөліктерінің энергияларының қосындысына теңдігі. Ал ықтималдықтар мультипликативті, яғни жүйе күйлерінің ықтималдығы оның бөліктерінің күйлерінің ықтималдықтарының көбейтіндісіне тең. Аддитивтік шартты қанағаттандыру үшін, ықтималдық пен энергияның арасында сызықтық байланыс болу керек.

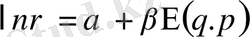(7. 2)

мұндағы - тұрақты шамалар. Квазитәуелсіз бөліктердің энергиялары Е ₁ , Е ₂ , . . . болса, тұтас жүйенің энергиясы Е= Е ₁ +Е ₂ + . . . болады, ал үлестірімділік үшін

ln ρ= ln ρ ₁ + ln ρ ₂ + . . . =ln(ρ ₁ ·ρ ₂ · . . . )

Осы формулалар арқылы жоғарыдағы шарттарды қанағаттандыруға болады. Потенцирлеп, (7. 2) -ден табатынымыз:

немесе тұрақтыларды басқаша белгілеп,

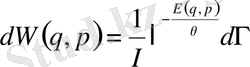; (7. 3)

Мұнда І=e ^-α және β=1/θ деп белгіленген. Бұл формула Гиббстің классикалық канондық үлестрімдігін бейнелейді. Гиббстің канондық үлестрімдігін микроканондық үлестрімдігінен де қорытып шығаруға да болады. Гиббстің канондық үлестрімдігін қорытудың негізінде де, микроканондық үлестрімдігіндегідей, статистикалық физиканың постулаты бар: « Жүйе бөлігінің күйлерінің ықтималдылығының энергияға бірмәнді тәуелді болуы энергиясы бірдей микрокүйлерінің ықтималдығы бірдей болғанда ғана мүмкін »

Гиббстің классикалық канондық үлестрімдігінің формуласындағы І-статистикалық интеграл деп аталады. Оның мәні нормалау шартынан табылады.

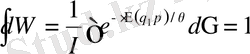бұдан

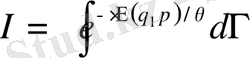
Сонымен, құрамы өзгермейтін жүйелерді Гиббстің микроканондық және канондық үлестрімдік заңдарымен сипаттауға болатынын көрсеттік. Үлестрімдіктің екеуі де қолданылуы мүмкін. Статистикалық физиканың есептерінде олар бірдей нәтиже береді. Тек микроканондық үлестрімдігі үшін энергияның флуктуациясы , ал канондық үлестрімдігі үшін - аз болса да шекті шама.

Термодинамикалық ықтималдық.

Статистикалық теңбе- теңдік күйге тұйық жүйе өздігінен өтеді. Бұл процесс жүйе микробөлшектерінің қозғалысы және өзара әсері нәтижесінде болады. Бұл процесс энергиялары бірдей, бірақ басқа параметрлері әртүрлі болатын теңбе-теңсіз микроскопиялық күйлерден біртіндеп өтуі арқылы іске асады деп есептеуге болады. (Айталық көлемі ішінде тығыздығы немесе температурасы не басқа параметрлері өзгерген кезде) Тұйық жүйенің теңбе - тең күйден ауытқу шамасын сипаттайтын және жүйедегі процесстердің бағытын сипаттайтын шаманы табу қажет.

Ең алдымен макрокүйлер дегеніміз не? Газды алар болсақ, берілген энергия, температура және тағы басқа параметрлермен сипатталатын күйлер жиыны- макрокүй деп аталады. Бұндай макрокүйге сәйкес келетін газдар жүйесінің күйлері көп. Олардың әрқайсысын микрокүй деп атайды. Олардың энергиялары, қысымдары, температуралары, көлемдері бірдей болғанмен, олар бірдей емес, бір- бірінен айырмашылығы молекулалардың орналасуының, жылдамдықтарының әртүрлілігінде. Айталық, газ ыдыстың бір жартысын толтыратын макроскопиялық күйді қарастырсақ, онда оған жарасымды микрокүйлер ішінде бірде - бірінде екінші жартысында молекула бар деп есептемеу керек. Ойша сондай микрокүйлер санын есептеу мүмкін делік. Бұл сан өте үлкен сан болуы керек. Ал газ ыдысты толық толтыратын макроскопиялық күйді қарастырсақ, онда оған сәйкес келетін микрокүйлер саны жарты ыдыс толтыратын микрокүйлер санынан әлдеқайда жоғары болатыны анық. Демек осы макрокүйлердің ықтималдығы микрокүйлер санына байланысты болуы керек. Осындай шаманы макрокүйлердің ықтималдығының сипаттамасы ретінде енгізуге болады. Берілген макрокүйге сәйкес келетін микрокүйлер саны макрокүйдің термодинамикалық ықтималдығы деп аталады.

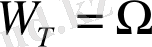(8. 1)

Сонымен бірге макрокүйдің статистикалық салмағы деп аталады.

Бұл шама өте үлкен. Оның статистикалық ықтималдықтардан айырмашылығы: барлық макрокүйлердің термодинамикалық ықтималдықтарының қосындысы бірге тең емес. Термодинамикалық ықтималдық статистикалық ықтималдыққа кері шама. Барлық микрокүйлердің ықтималдықтары тең болғандықтан, жүйенің берілген макрокүйінің ықтималдығы осы макрокүйге үйлесімді микрокүйлердің санына пропорционал.

Шынында, тұйық жүйе квазитәуелсіз бөліктерге бөлінетін болсын, әрқайсысы жуықтап теңбе-тең күйде болады делік. Постулатқа сәйкес кез- келген бөлігінің барлық микрокүйлерінің ықтималдықтары тең болып есептеледі. Тұтас жүйенің микрокүйін алу үшін бөліктердің белгілі бір микрокүйлеріндегі жиынын қабылдау керек. Бұл микрокүйінің ықтималдығы ρ=ρ ₁ ·ρ ₂ …. ρ _n бөліктердің микрокүйлердің ықтималдықтардың көбейтіндісіне тең.

Микрокүйлердің саны көп болғанмен, бұндай көбейтінділер сан жағынан тең, Бұл-жүйе микрокүйлерінің ықтималдықтарының өзара теңдігін білдіреді. Бұдан шығатын салдар: микрокүйлер ауысып тұрғанмен жүйенің қай макрокүйде ұзағырақ болуы оған сәйкес келетін микрокүйлердің санына байланысты. Олар неғұрлым көп болса, соғұрлым ұзағырақ болады. Мүмкін макрокүйлердің кейбіреулері жиі, кейбірі сирек болады. Сондықтан термодинамикалық ықтималдықтардың қатынасы макрокүйлердің іске асу ықтималдықтарын сипатттайды. Бұл қорытындылар дискреттік күйлер, дискреттік энергия деңгейлері туралы айтқанда ғана емес, үздіксіз энергия күйлері туралы айтқанда да дұрыс болады.

(8. 2)

Бұдан классикалық салада термодинамикалық ықтималдықтың өлшемі фазалық көлем болатындығы көрінеді. - берілген макрокүймен үйлесетін микрокүйлердің белгілі бір үздіксіз жиынына сәйкес келетін фазалық көлем. Көп бөлшектерден тұратын жүйелердің бір макрокүйі ақиқат болып келеді, ал басқа макрокүйлердің ықтималдықтары нөлге жуық. Сондықтан кез- келген тұйық жүйе берілген күйге орнығады да, өз бетімен бұл күйден шыға алмайды.

Теңбе-тең күйде термодинамикалық ықтималдық максималды .

Бұл макрокүйде жүйе барлық параметрлері бойынша біртекті болады. Теңбе-теңдікте ішкі қозғалыс толастамайды, бірақ микрокүйлер ауысып тұрғанмен, макрокүй өзгермейді. Тәуелсіз жүйелер үшін термодинамикалық ықтималдық мультипликативті шама болып табылады. Яғни екі тәуелсіз жүйенің бірі 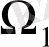микрокүйлердің біреуінде, ал екіншісі 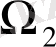микрокүйлердің бірінде орналаса алатын болса, онда 2 жүйені біріктіргенде, жүйенің микрокүйлерінің саны болады. Сондықтан ол үшін 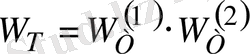болады. Есептеулерде аддитивті шаманы қолданған ыңғайлы. Бұндай шама- энтропия болып табылады. Екі шаманың көбейтіндісінің логарифмі әрбір шаманың логарифмдерінің қосындысына тең болатындықтан, энтропия термодинамикалық ықтималдықтардың логарифміне пропорционал болуы тиіс:

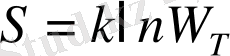(8. 3)

Бұл өрнек Больцман формуласы деп аталады; k- Больцман тұрақтысы, k =-1, 38∙10 ²³ дж/К. Больцман берген анықтамасына сәйкес энтропия - жүйенің бей берекетсіздігінің өлшемі. Шамалардың үздіксіз спектріне көшкен кезде (классикалық физика) жүйенің күйлерінің интервалы ұғымы қолданылады. Егер жүйе энергиясы интервалында болса, энтропия

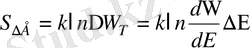(8. 4)

Мұнда - энергиясы 0-ден Е-ге мәндеріне сәйкес келетін жүйенің күйлерінің саны. Бір кванттық күйге фазалық кеңістікте сәйкес келетін ұяшықтың көлемін ескерейік.

және 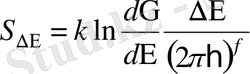(8. 5)

Классикалық статистикада жүйе энергиясы берілген жағдайда энтропия:

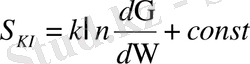(8. 6)

Сондықтан S _кл - әрқашан аддитивті тұрақтыға дейінгі дәлдікпен анықталады. Өзімен өзі тұрған тұйық жүйе ықтималдығы төмен күйден ықтималдығы жоғары максималды күйге көше отырып, ең ықтимал теңбе-тең күйге келеді. Бұл кезде жүйенің энтропиясы өседі. Теңбе- теңдікте бұл шама экстремумдық мәніне ие болады. Теңбе- тең күйден жүйе өздігінен шыға алмайтыны- энтропияның максимум мәнінен төмен мәніне жүйе өздігінен өте алмайтындығының салдары болып табылады.

Қайтымды және қайтымсыз процестердегі энтропия.

Адиабатты процесс-жылу беру арқылы энергия өзгерісі болмайтын процесс процесс теңбе-тең болсын. Энтропия жүйенің теңбе-тең күйде максималды мәнге ие болады. Барлық теңбе-теңсіз процесстердің бағыты бір -энтропияны өсіретін бағытта болады. Энтропия жүйе теңсіздігінің шамасын көрсетеді.

Энтропия ұғымы үш салада: термодинамикада, статистикалық физикада және кибернетикада қолданылады. Термодинамикада энтропияның анықтамасы:

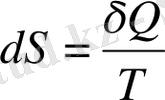(9. 1)

Жүйе бір теңбе-тең күйден екінші теңбе-тең күйге көшсе:

Ал кері қайтып келсе

(9. 2)

Бірінші процесс , екінші 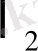-болсын. Теңбе-тең күйлерден өтетін процесті кері бағытта өткізгенде, бұрыңғы өткен күйлерден қайта өткізу мүмкін болса, бұндай процесс қайтымды деп аталады. Осы шарт орындалса, яғни -қайтымды процесс болса, онда 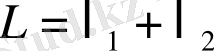қайтымды цикл болады:

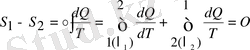(9. 3)

Бұдан: 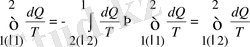(9. 4)

және 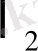процестері қайтымды болып, басқа жағынан бұлар әртүрлі болғандықтан, (9. 4) теңдіктен көретініміз: бір күйден екіншісіне өткенде, өту жолы қандай болса да, 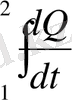интегралы бірдей мәнге ие болады. Демек, бұл шама жүйе күйіне ғана тәуелді. Қандай да шамалардың өзгерістері тек жүйе күйлеріне тәуелді болып, ал екі күйдің арасындағы жолдан тәуелсіз болса, бұндай шамаларды күй функциялары деп атайды, олардың өзгерістерін d U, d S деп белгілейік. Ал шамалардың өзгерістері бір күйден екіншісіне қандай процесс нәтижесінде өткендігіне тәуелді болса, бұндай шамаларды процесс функциялары деп атайды. Мысалы: жылу, жұмыс және т. б., олардың өзгерістерін dQ, dА емес, δ Q, δ А деп белгілейік. Сонымен энтропия күй функциясы болып отыр. Термодинамикада энтропия жай формальді функция, бірақ теориялық қорытуларда және практикалық есептеулерде кең қолданылатындықтан өте үлкен орын алады.

Энтропияның физикалық мағынасын статистикалық физика ашады. Энтропияны өзгертетін бір фактор - жылу алмасу: >O болғанда ds >O, яғни жылу жұтқанда энтропия артады, ал 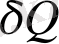<О болғанда ds <O, - жылуды маңайдағы ортаға бергенде энтропия азаяды. «Энтропия» терминін Клаузиус енгізген болатын: Эн (ергия) тропе (түрленуі) мағынасын береді. Энтропия белгілі бір тұрақтыға дейінгі дәлдікпен анықталған:

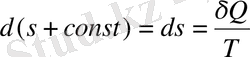(9. 5)

Аддитивті тұрақтыны Нэрнст теоремасының көмегімен анықтайды. Жүйеге жылу бергенде жүйенің ішіндегі бөлшектердің қозғалысындағы ретсіздігі және ішкі құрылымның тәртіпсіздігі күшейеді, мысалы: кристалды қыздырғанда жылулық тербеліс амплитудасы күшейіп, ақырында, белгілі бір температурада, кристалдың құрылымы бұзылады, - атомдар тербелісіне атомдардың бір нүктеден екіншісіне секірулері қосылады. Сөйтіп, энтропия өседі. Сонымен, энтропия- жүйенің ішкі құрылымындағы ретсіздігінің және құрамындағы бөлшектердің қозғалысындағы бей-берекетсіздігінің өлшемі болып табылады. Осы тұрғыдан энтропияның термодинамикалық және статистикалық физикадағы анықтамалары ұштасады.

Механикалық процесті тура және кері бағытта бірдей өткізуіміз мүмкін. Мұндай процессті қайтымды процесс деп атайды. Термодинамикада тұйық процессті бірдей теңбе−тең күйлер арқылы тура және кері бағытта өткізуіміз мүмкін болса, қайтымды процесс , ал мүмкін болмаса, онда мұндай процесс қайтымсыз процесс деп аталады. Ол жөнінде «тура бағытта жүреді, кері бағытта жүрмейді»- деген анықтама дұрыс емес. Қайтымсыз процессті тура және кері бағытта өткізуіміз мүмкін, тек кері бағыттағысы өздігінен өте алмайды. Мысалы: денені қыздыру (не суыту) процестерінің біреуі өздігінен өтсе, екіншісі, яғни кері процесс, тоңазытқышта (не пеште) өтеді. Қайтымды процесс квазистатикалық процесс ( § 11) болады және диссипативтік эффектілермен қабаттаса жүрмейді. Мысалы: турбуленттік, үйкеліс немесе электр кедергісі сияқты қайтымсыз процестерге, яғни тұтқыр сұйықтың турбулентті араласуы, электр зарядтың кедергіден өтуі, газдың вакуумге еркін таралуы, екі газдың араласуы сияқты процестер, серпімсіз деформацияда энергия шығыны, поляризация мен магниттелу кезінде процесстер жатады. Бұларға кері процесстің өздігінен өтуін көзге елестету қиын. Бұндай процесс мүмкін болса да, тек сыртқы әсерлердің көмегімен өтеді. Демек, ол өткеннен кейін маңайдағы денелердің күйінде өзгеріс болу керек. Процессті жүргізіп, одан кейін жүйені кері бағытта сол жолмен алып келгенде, маңайдағы ортада өзгерістер болса, бұл процесс қайтымсыз , маңайдағы ортада өзгерістер болмаса, - қайтымды болып табылады. Энтропияның өсу процесі қайтымсыз процесспен байланысты. Жүйенің және оның әсерлескен барлық денелердің энтропиясы өседі.