Беріліс функциясы және сызықты дифференциалдық теңдеулердің стандартты формасы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 10 бет
Таңдаулыға:

Қазақстан Республикасы білім және ғылым министрлігі

Л. Н. Гумилев атындағы Еуразия ұлттық университеті

Ақпараттық технологиялар факультеті

Жүйелік талдау және басқару кафедрасы

2ewds

СӨЖ

Пән: Сызықты автоматты реттеу жүйелері.

Тақырыбы: Беріліс функция. АБЖ дифференциалдық теңдеулердің стандартты формасы.

Орындаған: АБ- 39/7 студенті

Жақсылық Қ. Ж.

Тексерген: аға оқытушы Шукирова А. К.

Нұр-Сұлтан 2020

Сызықты дифференциалдық теңдеулерді жазу формасы. Беріліс функциясы.

Автоматты басқару жүйелерін сипаттау кезінде сызықты дифференциалдық теңдеулердің символикалық формасы кеңінен қолданылады.

(3. 1)

d/dt=p, d ⁱ /dt ⁱ =p ⁱ түрлендірулерін қолданып (3. 1) теңдеуін келесі түрде жазайық

(3. 2)

(3. 3)

Белгілеулер енгіземіз , , . Осы белгілеулердің көмегімен (3. 3) теңдеуін келесідей ықшамды түрде жазуға болады:

. (3. 4)

Q(p) - меншікті оператор

R ₁ (p) және R ₂ (p) - қоздыру операторлары

Беріліс функциясы. Қоздыру операторының меншікті операторға қатынасы беріліс функциясы немесе операторлық формадағы беріліс функциясы деп аталады.

(3. 1) теңдеуімен немесе (3. 2) - (3. 4) теңдеулерімен сипатталатын буынды төмендегідей сипаттауға болады.

х кіріс шамасы бойынша W ₁ (p) беріліс функциясы:

(3. 5)

және z кіріс шамасы бойынша W ₂ (p) беріліс функциясы

(3. 6)

Беріліс функциясы немесе Лаплас кескін формасындағы беріліс функциясы деп бастапқы нолдік шарттар кезінде шығыс шаманың кіріс шамаға қатынасын айтамыз.

Мысал. Лаплас кескін формасындағы беріліс функциясын табайық.

.

, (3. 8)

Мұндағы Y(s) =L{y(t) }, X(s) =L{x(t) }, Z(s) =L{z(t) }.

, . (3. 9)

. (3. 10)

Сызықты дифференциалдық теңдеулердің стандартты формасы.

, (3. 11)

где ; ; ; ; .

Т ₀ , T ₁ және T ₂ -уақыт тұрақтысы

k ₁ және k ₂ а коэффициенты - беріліс коэффициенттері

(3. 11) келесідей жазуға болады:

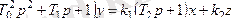
Беріліс функция. Беріліс функцияны анықтау.

Лаплас бойынша ДТ түрлендіру айнымалы функцияны анықтауға және жүйенің динамикалық қасиетін анықтауға мүмкіндік береді.

Мысалы, операторлы теңдеу

3s ² Y(s) + 4sY(s) + Y(s) = 2sX(s) + 4X(s)

Онда түрлендіруге болады, жақшаның сыртына бірі біріне бөлу арқылы X(s) және Y(s) шығарамыз:

Y(s) *(3s ² + 4s + 1) = X(s) *(2s + 4)

.

Алынған функцияны айнымалы функция деп атайды.

Айнымалы функция деп бастапқы нөлге тең кіріс X(s) бейнеленуімен шығыс әрекет Y(s) бейнеленуімен әрекеттерімен бейнеленген қатынастарды айтамыз.

(3. 4)

Айнымалы функция болып кешенді айнымалы рационалды-бөлшекті функциясын айтамыз:

,

мұнда B(s) = b ₀ + b ₁ s + b ₂ s ² + … + b _m s ^m - тақ санның полиномы,

А(s) = a ₀ + a ₁ s + a ₂ s ² + … + a _n s ⁿ - жұп саның полиномы.

Жұп саның полиномымен анықталынатын айнымалы функция келесі тәртіпте болады (n) .

Бұдан (2. 4) шығыс сиганлын бейнелеу келесі түрде табуға болады

Y(s) = W(s) *X(s) .

Жүйенің айнымалы функциясы толығымен оның динамикалық қасиетін анықтаса, онда АРЖ бастапқы тапсырмасын есептеу оның айнымалы функцияны анықтауға әкелінеді.

Типті тізбектердің мысалы.

Жүйенің тізбегі деп динамикалық қатынасында нақты бір қасиеттерімен ерекшелінетін элемент. Жүйені реттеу тізбегі әртүрлі физикалық негізінен тұрады (электрлік, пневматикалық, механикалық т. б), бірақ та оның тек бір тобымен ғана қатыстурумыз қажет. Тізбекте сигналдардың кіріс және шығыс қатынастарын бірдей айнымалы функциямен анықтауға болады.

Қарапайым типті тізбек:

· күшейткіш,

· интегралдау

· дифференциялдау,

· апериодиялық,

· тербелмелі,

· кешігу.

1) Күшейткіш тізбек.

К

у

t

3. 1-сурет.

Тізбек кіріс сигналды К рет күшейтеді. Тізбектің теңдеуі у = К*х, айнымалы функция W(s) = К.

К параметрін күшейткіш коэффициенті деп атайды.

Мұндай тізбектің шығыс сигналын К реттік күшейтілген кіріс сигналды қайталайды. (сур. 3. 1) .

Осындай тізбектің мысалдар болып :механикалық, датчиктер, инерционсыз күшейткіштер т. б.

2) Интегралдау.

2. 1) Идеалды интегралдау.

Идеалды интегралданатын шығыс шама кіріс шаманы интегралдаутізбегіне пропорционал болады.

у

t

3. 2- сурет.

; W(s) =

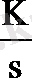
Тібектің кіріс берілісіне шығыс сигналдың әсері орнықты түрде өсіп отырады. (сурет. 1. 16) .

Бұл тізбек астатикалық, яғни тұрақтандыру режимінен тұрмайды.

2. 2) Шынайы интегралданатын.

у

t

3. 3-сурет.

Бұл тізбектің айнымалы функциясы келесі түрде болады:

W(s) = .

Айнымалы сипаттамасы идеалды тізбекке қарағанда қисық болып келеді. (сурет. 3. 3) .

Интегралданатын тізбектің мысалы болып тәуелссіз қоздыруы бар орнықты тоқты қозғалтқыш болып табылады. Егер де кіріс әрекеттер түрінде статордың кернеу қорегін алатын болсақ, ал шығысына ротордың айналу роторын алатын болсақ интегралданатын тізбекке тікелей әсері болады.

3) Дифференцирленетін.

3. 1) Идеалды дифференцирленетін.

Шығыс шамасы уақыт бойынша кірісінің туындысына пропорционал:

; W(s) = K*s

Сатылы кіріс сигналы кезінде шығыс сигналы өз алдына импульсті құрайды (d-функцию) .

3. 2) Шынайы дифференцирленетін.

у

t

3. 4 -сурет.

Идеалды дифференцирленетін тізбек физикалық түрде таралмайды. Дифференцирленетін тізбекке кіретін көбіне нысанаілер шынайы тізбекке кіреді. Айнымалы сипаттама мен айнымалы функция келесі түрде болады :

W(s) = .

4) Апериодиялық (инерционное) .

Бұл тізбекке ДТ сәйкес келеді:

; W(s) =

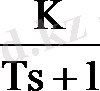
Бұл тізбекке шығыс шамасының өзгеру сипаттамасын анықтаймыз оның кірісіне сатылы әрекетінің шамасы х ₀ .

Сатылы әрекетті бейнелеу: X(s) = . Шығыс шаманың бейнеленуі :

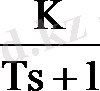
Y(s) = W(s) X(s) = = K x ₀ .

Бөлшекті қарапайым түрге жіктейміз:

= + = = - = -

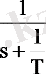
Кесте бойынша бірінші бөлшектің нақтысы: L ^-1 { } = 1, екіншісі:

L ^-1 { } =

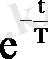
Онда соңында алатынымыз:

y(t) = K x ₀ (1 - ) .

Орнықты Т орнықты уақыт деп атайды.

Көбіне жылу нысанаілер апериодиялық тізбектер болып табылады. Мысалы, электрлік пештің кірісіне кернеудің берілісінде температура өзгереді (сурет. 1. 19) .

у

t

К

3. 5-сурет 3. 5

5) Тербелмелі тізбек ДТ түрде болады

y

t

K ^. x ₀

T ₁ < 2T ₂

T ₁ ³ 2T ₂

3. 6-сурет

,

W(s) = .

Амплитуда х ₀ сатылы әрекеттердің берілісі айнымалы қисығы келесі түрде

болады (Т ₁ ³ 2Т ₂ ) немес тербелмелі (Т ₁ < 2Т ₂ ) .

6) Кешігу.

y(t) = x(t - t), W(s) = e ^-ts

Шығыс шамасы кіріс шамасының х нақтылығын қайталады, ол кешігумен қатар t жүреді . Мысалы: конвейер арқылы жүктің қозғалысы, құбырөткізгіш бойынша сұйықтың қозғалысы.

Тізбектің қосылыс.

Зерттелетін нысанда қарапайым функционирлеу мақсатында тізбектерге бөлінген, айнымалы функцирлеу кейін әр тізбек үшін нысанаіні бір айнымалы функцияға қосу тапсырмасы тұрады. Нысаның айнымалы функциясының түрі тізбектердің қосылыс жалғануларымен байланысты жүреді:

1) Тізбектей жалғанған қосылыс.

W ₁

W ₂

W ₃

х

у

3. 7-сурет

W _об = W ₁ ^. W ₂ ^. W ₃ …

Тізбектей жалғанған қосылыстарда олардың айнымалы функциясы көбейеді.

Параллелді қосылыс.

W _об = W ₁ + W ₂ + W ₃ + …

Параллелді қосылыс кезінде олардың айнымалы функциялары қабаттасады.

W ₁

W ₂

W ₃

х

у

3. 8-сурет. 3. 8

3) Кері байланыс

W ₁

W ₂

х

у

3. 9-сурет. 1. 23

Тапсырма бойынша айнымалы функция (х) :

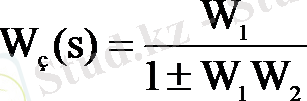
«+» кері байланысқа сәйкес,

«-» - тура байланысқа сәйкес.

Нысанаінің айнымалы функциясын анықтау үшін, яғни күрделі тізбектің қосылысы болғанда, схеманың ұлгайған түрін қолданады немесе Мезон формуласын түрлендіреді.

АРЖ беріліс функциясы. Ауыспалы қисық бойынша нысаның беріліс функциясының параметрлерін анықтау. Жиліктік сипаттама. Жиліктік сипаттаманы анықтау. Логарифмді жиліктік сипаттама.

W _p

W _y

x

e

u

y

f

4. 1-сурет

АРЖ құрылымдық схемасын есептеу мен зерттеуде эквивалентті түрлендіру жолы қарапайым стандартты «нысан- регулятор» түріне келтіріледі.

Бұл өте қажет, біріншіден жүйеде математикалық тәуелділікті анықтау үшін, екіншіден барлық жүйеде инжеренлік әдістер, есептеулер мен реттеуіштердегі параметрлерді зерттеулер осы стандартты құрылыммен жүргізіледі.

Жалпы жағдайда кез келген негізгі кері байланысты бірөлшемді АРЖ ұлғайтылған тізбектердің жолымен осы жолмен келтірілуі мүмкін.

Егер де жүйенің шығысы у кіріске берілмесе, онда біз реттегіштің тұйықталған жүйесін аламыз, ал айнымалы функция келесі түрде анықталынады:

W _¥ = W _p ^. W _y

(W _p - ПФ регулятор, W _y - ПФ басқару нысан.

W _¥

х

у

4. 2-сурет

Яғни, тізбектердің жалғануы W _p және W _y басқа тізбекпен W _¥ ауысуы мүмкін. Айнымалы функция Тұйықталған жүйенің айнымалы функциясын Ф(s) белгілеу қабылданған. Ол W _¥ арқылы есептелінеді:

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.