Су теңдестігі әдісі жөніндегі жалпы мәліметтер және оның қолданбалы мәні

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Жоспар:
Кіріспе
1. Су теңдестігі зертеулерінің дамуындағы негізгі кезеңдер
2. Су теңдестігі әдісі жөніндегі жалпы мәліметтер және оның қолданбалы мәні
Қорытынды
Қолданылған әдебиеттер

Кіріспе
Су теңдестігі жалпы материяның сақталу заңының бір ерекше түрі. Осы заңдылықтың негізінде жеке аумақтардағы, үлескіде немесе өзен алаптарының су теңдестігінін, кіріс, шығыс, жиналуын есептеп табуға мүмкіндік аламыз. Су теңдестігі өзен, көл, батпақ және басқа да су объектілерінің табиғи және антропогендік жағдайда гидрологиялық режимдерін зерттеу негізгі болып саналады. Өзен алабындағы су шаруашылық және агромелиоративтік шаралар қалыптасқан табиғи теңдестікті бұзуға айтарлықтай әсер етеді, яғни су теңдестігінің құрамының өзара қатынасы өзгеріске ұшырайды. Шаруашылық қызметтің әсерінен теңдестік теңдеуінің құрамына кіретін элементтердің өзгеріске ұшырау заңдылықтарын анықтауда су көздерінің қорларына әсерін бағалауға мүмкіндік береді. Бұл бағалау әсіресе су қорларын келешекте тиімді пайдалану үшін жоспарлау үлкен маңызға ие болады. Жер беті жер асты суайрыктарының сәйкес келуі көрші алаппен су алмасуының болмауын камтамасыз етеді (сурет 5.1).

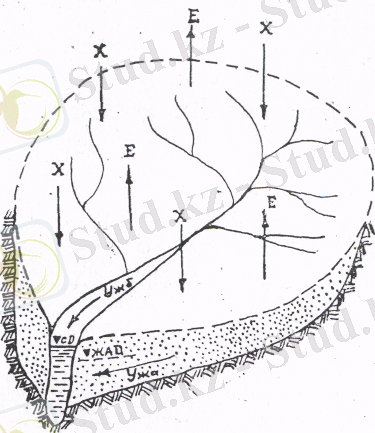
5.1-сурет - Өзен алабының нобайы.
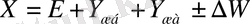Теңдеудің кіріс бөлігі жауын-шашыннан (X) тұрса, ал шығыс бөлігі -- булану (Е), жер беті (Үжб) және жер асты (Үжа) ағындыларынан тұрады. Булану (Е) деп бұл жерде конденсациядан қалған нәтиже алынады. Әдетте бұл элемент теңдеудің басқа кұрамына карағанда өте аз мөлшерде болады. Алаптың топырақ кұрамы, арна, көл және батпақтардағы ылғалдылықтың өзгеруі деп белгіленеді. Нәтижесінде өзен алабының су тендестігінің теңдеуі төмендегідей өрнектеледі

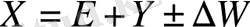
Теңдеудегі алдындағы + белгісі су жиналуын білдірсе, ал -- белгісі алаптағы ылғалдың шығындалуын көрсетеді. (Үжб+Үжа) косындысы ағындыны (Ү) береді, олай болса (5.1) теңдеуі төмендегіше түрленеді.

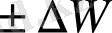Көпжылдық мерзім үшін өзен алабының шекарасында ылғалдың өзгеруінің шегі нөлге ұмтылады, яғни --0, ал жауын-шашын, булану және ағынды өзендерінің орташа мәніне сәйкес келеді, яғни Х0, Е0, Ү0 немесе Х0 = E0 + Y0. Бұл теңдеуден шығатын қорытынды: көпжылдық мерзімде алапқа түсетін жауын-шашын түгелімен ағынды мен булануға шығындалады. Бұл қорытынды тек ірі; өзен алаптары үшін және өзен арнасы барлық сулы топырақ қабаттарын толық дренаж жасалынған өзен арналарында орындалады. Ал, уақытша өзендер үшін ағындының жер асты бөлігі (Үжа) тәжірибеде нөлге шамалас, сондықтан осындай өзен алаптары үшін теңдеу төмендегіше өрнектеледі

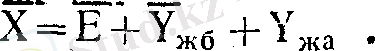
Яғни, кішігірім өзен алаптарында жауын-шашын булануға, жер беті ағындысына және жер асты суларының қорын (Үжа) толықтыруға жұмсалады екен. Себебі уақытша өзен арнасының саяздығынан жер асты суларымен қоректенуге шамасы келмейді.
Енді, тұйық өзен алабын қарастырып көрейік, яғни өзендер құятын, ал бірде-бір өзен ағып шықпайтын көлді қарастырсак, онда Ү0=0 екенін көреміз. Бұл жағдайда теңдеу былайша өрнектеледі.
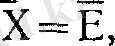немесе көпжылдық мерзімде тұйық алаптардағы жауын-шашын түгелімен булануға жүмсалады. Тәжірибеде су теңдестігінің теңдеуі оның құрамын бақылау немесе сәйкестендіру үшін ғана емес, сонымен бірге белгісіз жане өлшенуі қиын көрсеткіштерді анықтау үшін де пайдаланылады. Расында, өзен алабының шеңберінде екі жауын-шашын (X) мен қосынды ағынды (Ү) ғана ткелей өлшенуі мүмкін. Ал, бүкіл алаптың беткейінен буланған ылғал көлемін алатын болсақ, бұл әзірге мүмкін емес. Әр түрлі жерлерге қойылған буландырғыштардың көмегімен біз буланудың тек шамалық мәнін таба аламыз. Алаптың бетінен буланған ылғалды (Е) су тендестігінің теңдеуінен көпжылдық мерзім үшін тікелей айтарлықтай қиындықсыз анықтауға болады. Ал, қысқа мерзімдік булану мөлшерін анықтау үшін, жауын - шашын мен ағындыдан өзге, алаптағы ылғал қорының құбылмалылығын 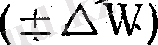да білуіміз керек. Су теңдестігінің теңдеуінен анықталған алаптың бетінен буланған ылғалдың мәнін есептеу барысында оған айқындаушы факторларға байланысты (көбінесе ауаның температурасы мен ылғалдылығы) одан әрі қорытындылауға, тұжырымдай беруге болады. Бұл байланыстардың негізінде гидрологиялық жағьнан зерттелмеген өзен алаптары үшін көпжылдық ағындының (Ү) орташа мәнін өлшенген метеорологиялық көрсеткіштердің (жауын-шашын, ауаның. температурасы және ылғалдылығы) көмегімен бағалау мүмкіндігіне қол жеткіземіз.

1. Су теңдестігі зертеулерінің дамуындағы негізгі кезеңдер
Біздің планетамыздың су теңдестігі және табиғаттағы су айналымы мәселесіне қатысты түсінік өте ерте заманда пайда болған. Бізге жеткен мәліметтерге сүйенсек, атомдық ілімнің негізін салушы Демокрит (б.з.д. 460-370 жж.) Ніл өзенінің жайылуын метеорологиялық құбылыстармен байланыстырған екен. Платонның пікірінше, құрлықтағы барлық судың қайнар көзі теңіз суы болған. Ерте заманның ұлы ойшылы Аристотель Жер бетіндегі барлық судың қайнар көзі атмосферадағы ылғал екендігін айтып кеткен болатын: өзендер атмосфералық жауын-шашын және ауадағы атмосфералық ылғалдың конденсациялануы есебінен қоректенеді. Марк Витрувий Полион ең алғаш рет грунт суларының инфильтрациялық шығу тегі туралы идеяны негіздеген болатын. Сонымен қатар, ол буланудың, жауын-шашынның түзілуі және жаңбыр жаууының қозғаушы күші күн жылуы мен жер қойнауындағы қайнап, балқып жатқан массалар мен ауа стихиясы деп санаған болатын. Тит Лукреций Кар (б.з.д. 1 ғ.) Демокрит пен Аристотель көзқарастарын біріктіріп, өзен суларының атмосфералық шығу тегі туралы ой айтқан болатын. Ерте заманның натурфилософтары табиғаттағы су айналымының жекелеген бөліктерін дұрыс түсінгенімен, бұл құбылысты бір-бірімен байланысқан бірыңғай гидрологиялық цикл ретінде қарастыра алмады. Гидрология тек қана Қайта өрлеу дәуірінен бастап бағытты зерттеулер мен білімнің жүйелі түрде жинақталуының нысанына айналды. 1674 ж. француз жаратылыстанушысы П. Перро өзен алабының су теңдестігін есептеу арқылы гидрологиялық циклды сандық тұрғыдан түсіндіруге талпыныс жасады. Сена өзенінің жоғары алабы үшін жауын-шашын және ағынды мөлшерін өлшеп, өзен ағындысы атмосфералық жауын-шашынның 16 бөлігін құрайды және сол атмосфералық жауын-шашыннан пайда болады деген шешімге келді. Бұл өзен қоректенуі үшін жаңбыр суының жетіспейтіндігі жөнінде ерте заманнан қалыптасқан пікірді жоққа шығарған ең алғашқы су теңдестігі зерттеулері мен есептеулері болатын. 1974 ж. ЮНЕСКО шеңберінде ғылыми гидрологияның 300 жылдығы аталып өтткендігін айта кеткен жөн. 1686 ж. Француз физигі Э. Мариотт Перрон зерттеулерін жалғастыра отырып, Сена өзенінің бүкіл алабы үшін су теңдестігі есептеулерін жүргізді. Осылайша, П. Перрон және Э. Мариотт өзен алабы шегіндегі су айналымын зерттеудің ең алғашқы ғылыми негіздемесін жасады. Ағылшын геофизигі Галлей 1709 ж. ең алғаш рет Жер бетіндегі су айналымының кескіндемелік сұлбасын көрсетті. Ол Жерорта теңізі үшін су айналымы сұлбасын тұйықтай отырып, осы теңіз бетінен булану көлемін есептеген болатын. Оның мәліметтері бойынша теңіз бетінен булану шамасы теңізге келіп құятын өзен ағындысынан 3 есеге асып түсті. Ағылшын ғалымы Д. Дальтон (1802 ж.) су бетінен булануды есептеуге арналған ең алғашқы теориялық формуланы ұсынды.
Каспий теңізі су теңдестігінің ең алғашқы ғылыми негізделген есептеуін орыс ғалымы А.И. Воейков (1884 ж.) жүргізді. Ол орташа көп жылдық жыл үшін мынадай теңдеу ұсынды:
Е = Х + У, (3)
мұндағы Е, Х, ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.