Stud.kz

Гаусс формуласы. Валлис формуласы. Санның трансценденттілігі


Жұмыс түрі:  Курстық жұмыс
Тегін:  Антиплагиат
Көлемі: 12 бет
Таңдаулыға:   

Қазақстан Республикасының Білім және Ғылым министрлігі

Ө. Сұлтанғазин атындағы Қостанай мемлекеттік педагогикалық университеті

Жаратылыстану-математика факультеті

Физика-математикалық пәндер кафедрасы

Узакбаева Улмекен Габиткызы

Гаусс формуласы. Валлис формуласы. Санның трансценденттілігі

Курстық жұмыс

Ғылыми жетекші: Доспулова У. К.

аға оқытушы

Қостанай, 2019ж

Мазмұны

Кіріспе . . . 3

1. Негізгі бөлім . . . 4

1. 1. Гаусс формуласы . . . 4

1. 2. Валлис формуласы . . . 7

1. 3. Санның трансценденттілігі . . . 10

2. Практикалық бөлім . . . 13

Қорытынды . . . 16

Қолданылған әдебиеттер тізімі . . . 17

Кіріспе

Гаусс формуласы - интегралдарды түрлендіруде айнымалыны алмастыру үшін тағы бір мысал ретінде Гаусс орнатқан тамаша формуланы қолдана аламыз.

Валлис формуласы - π 2 = lim ⁡ n → ∞ [ 2 n ! ! ( 2 n − 1 ) ! ! ] 2 • 1 2 n + 1 \ \ \ \ \ \frac{\pi}{2} = \lim_{n \rightarrow \infty}{\left\lbrack \frac{2n!!}{(2n - 1) !!} \right\rbrack^{2} \bullet \frac{1}{2n + 1}}

Бұл Валлис формуласы. Ол оңай есептелетін рационалды нұсқаның шегі түрінде π санының бірінші көрінісі ретінде тарихи қызығушылық бар. Теориялық зерттеулерде оны қазір де пайдаланады. π санын жуықтап есептеу үшін, қазір мақсатқа жылдам апаратын әдістер бар.

Санның трансценденттілігі - (лат. transcendere-ауысу, асып кету) - бұл нақты сан, бірақ алгебралық емес, басқаша айтқанда, рационалды коэффициенттердің көпмүшелі түбірі емес сан.

Зерттеудің өзектілігі: курстық жұмыстың мазмұнының ғылыми құндылығын арттыру және оның негізінде пәнге деген қызығушылығын арттырып, өз бетінше іздену. Білім, білік, дағды алуын қамтамасыз етуге, жеке шығармашылық қабілеті дамуы үшін жағдай туғызу.

Мақсаты: Интегралдың шектерін есептеуде Гаусс, Валлис формулаларын қолдану.

Міндеті:

- Берілген тақырыптардың теориялық бөлімін қарастыру.

- Гаусс және Валлис формулаларын есептер мен мысалдарда қарастыру.

Зерттеу объектісі: Интеграл шектері. Санның трансценденттілігі.

Зерттеу пәні: Гаусс формуласы. Валлис формуласы. Санның трансценденттілігі.

Зерттеу әдістері: Талдау нәтижесінде алынған мәліметтерді бақылап, тақырып бойынша әдебиеттерді зерттеу

Құрылымы: курстық жұмыс кіріспеден, негізгі бөлімнен, практикалық бөлім, қорытынды және қолданылған әдебиеттер тізімінен тұрады.

1. 1 Гаусс формуласы

Гаусс әдісі-интегралдау түйіндерін арнайы таңдау арқылы интерполяциялық формулалар негізінде әдіс дәлдігінің алгебралық тәртібін жоғарылатуға мүмкіндік беретін сандық интегралдау әдісі. Гаусс әдісі алгебралық дәлдікті интегралдау тораптарының осы санына барынша жетуге мүмкіндік береді. Мысалы, екі тораптар үшін 3-ші дәлдік реті

әдісін алуға болады, ал 2-ші тәртіптен жоғары әдістің бірдей тұрған тораптары үшін алу мүмкін емес. Жалпы жағдайда, пайдалана отырып, нүктелердің n, дәлдік тәртібімен әдісті алуға болады 2n-1 . Гаусс әдісі тораптарының мәндері n нүктелер n дәрежесі Полинома Лежандр түбірі болып табылады. Таразылардың мәндері мынадай формула бойынша есептеледі

мұнда P ′ n P'n\ - Полином Лежандрдың алғашқы туындысы. n=3 үшін тораптар мен салмақтар мынадай мәндерге ие : x 1 , 3 = ± 0. 6 , x 2 = 0 x_{1, 3} = \pm \sqrt{0. 6\ }, x_{2} = 0 салмағы : a 1 , 3 = 5 9 , a 2 = 8 9 . \ \ a_{1, 3} = \frac{5}{9}\, a_{2} = \frac{8}{9}. (Полином кесіндіде анықталған [ − 1, 1 ] ) . Гаусс әдісі ең танымал бес нүкте.

Айнымалыны ауыстыру үшін тағы бір мысал қарастырайық Гаусспен белгіленген керемет формула (С. F. Gauss) интегралды түрлендіру.

G = ∫ 0 π 2 d φ a 2 sin ⁡ φ 2 + b 2 sin ⁡ φ 2 ( a > b > 0 ) G = \int_{0}^{\frac{\pi}{2}}{\frac{d\varphi}{\sqrt{a^{2}{\sin\varphi}^{2} + b^{2}{\sin\varphi}^{2}}}\ \ \ \ \ (a > b > 0) }

Мұнда қойыңыз

sin ⁡ φ = 2 a sin ⁡ θ ( a + b ) + ( a − b ) sin ⁡ θ 2 \sin{\varphi = \frac{2a\sin\theta}{(a + b) + (a - b) {\sin\theta}^{2}}}

θ , 0 \theta, \ 0 2-ден π 2 ж ә н е φ − г е \frac{\pi}{2}\ және\ \ \varphi - ге өзгергенде сол өсетінін көру оңай шегінде. Дифференциалдаймыз:

cos ⁡ φ d φ = 2 a ( a + b ) − ( a − b ) sin ⁡ θ 2 [ ( a + b ) + ( a − b ) sin ⁡ θ 2 ] 2 cos ⁡ θ d θ \cos{\varphi d\varphi = 2a\frac{(a + b) - (a - b) {\sin\theta}^{2}}{\left\lbrack (a + b) + (a - b) {\sin\theta}^{2} \right\rbrack^{2}}}\cos{\theta d\theta}

Бірақ,

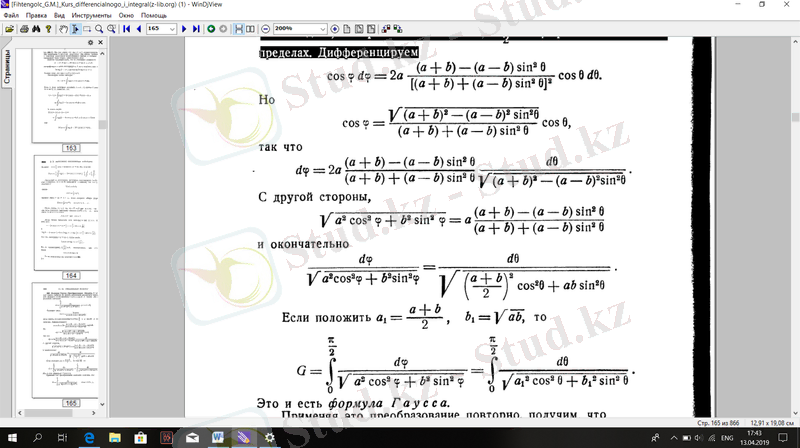
Сондықтан

Екінші жағынан

Және түпкілікті

Егер

болса, онда

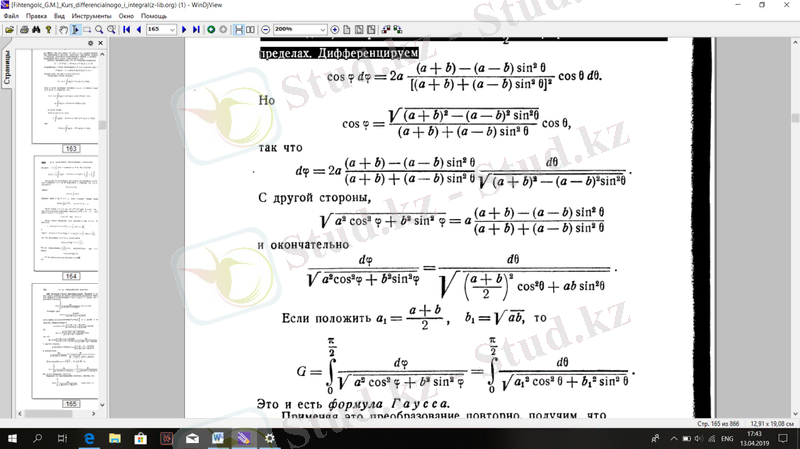
Бұл Гаусс формуласы, оны қайттан түрлендірсек:

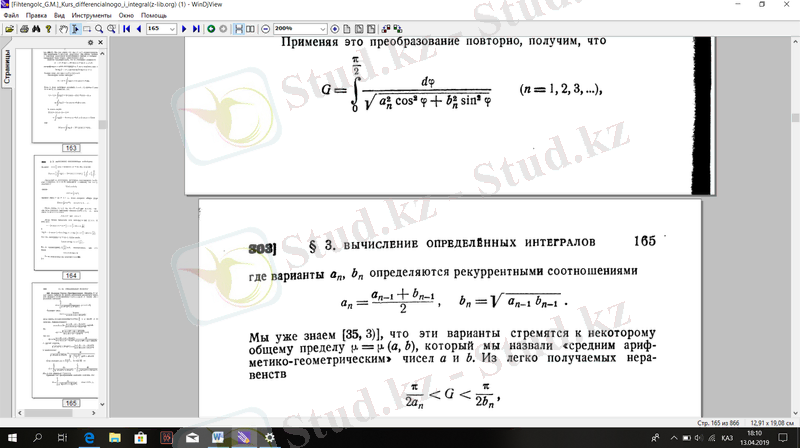
мұнда a n , b n a_{n, }b_{n} нұсқалары рекурренттік қатынаспен анықталады

Біз білеміз [35, 3) ], бұл опциялар кейбір біз "орташа ариф" деп атаған μ = μ ( a , b ) \mu = \mu(a, b) \ жалпы шегі- a және b сандар. Жеңіл алынатын теңсіздік

шегіне өтіп, табатынымыз G = π 2 μ ( a , b ) G = \frac{\pi}{2\mu(a, b) } , одан μ ( a , b ) = π 2 G \mu(a, b) = \frac{\pi}{2G} G интегралы бірінші текті толық эллиптикалық интегралға келтіріледі

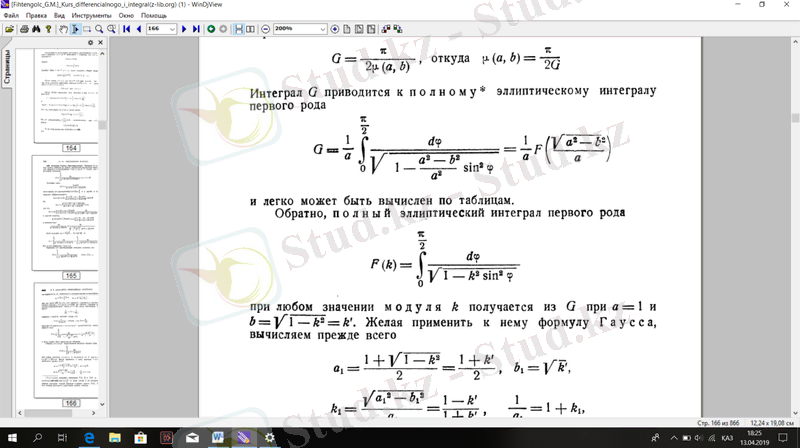
кесте бойынша есептеу оңай. Кері, толық эллиптикалық интеграл бірінші

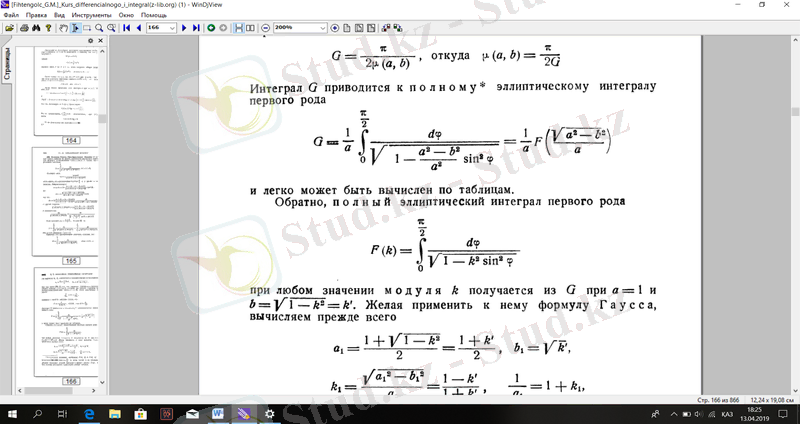
к модулінің кез келген мәні G арқылы а = 1 және b = 1 − k 2 = k , b = \sqrt{1 - k^{2}} = k^{, } . Оған Гаусс формуласын қолдануға болады, ең алдымен есептейміз

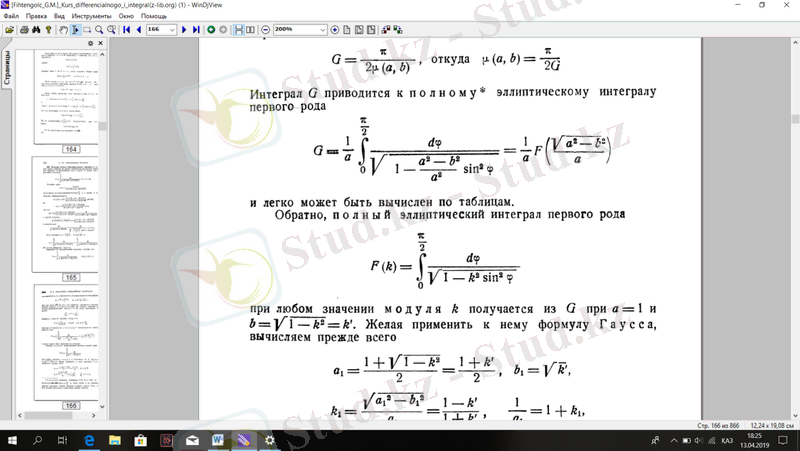
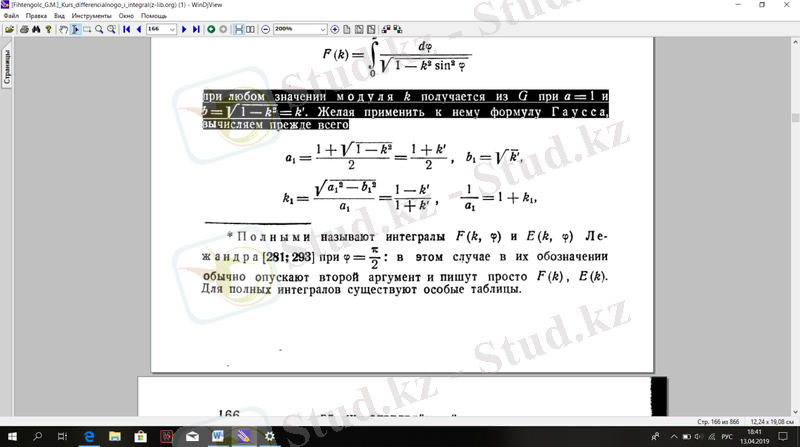
Сондықтан

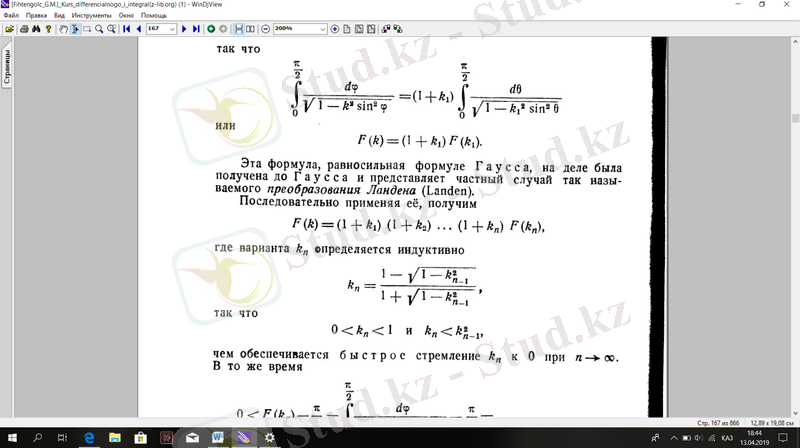
Немесе

Бұл формула, Гаусс формуласына тең, іс жүзінде Гауссқа дейін алынды және Ланден (Landen) өзгеруінің жеке жағдайын білдіреді. Оны дәйекті түрде қолданамыз

мұнда k n k_{n\ } нұсқалары индуктивті анықталады k n = 1 − 1 − k n − 1 2 1 + 1 − k n − 1 2 k_{n} = \frac{1 - \sqrt{1 - k_{n - 1}^{2}}}{1 + \sqrt{1 - k_{n - 1}^{2}}} , сондықтан, 0 < k n < 1 < k_{n} < 1\ \ \ \ және k n < k n − 1 2 , k_{n} < k_{n - 1}^{2}\, кезінде k n k_{n} -ден 0-ге жылдам ұмтылу қамтамасыз етіледі.

Сол уақытта

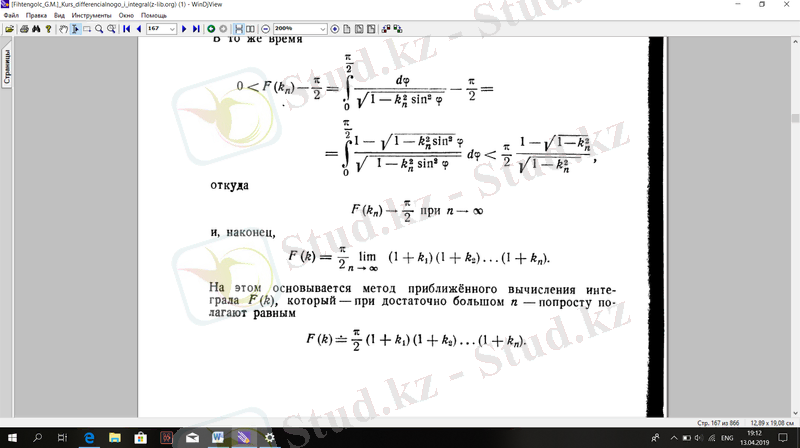
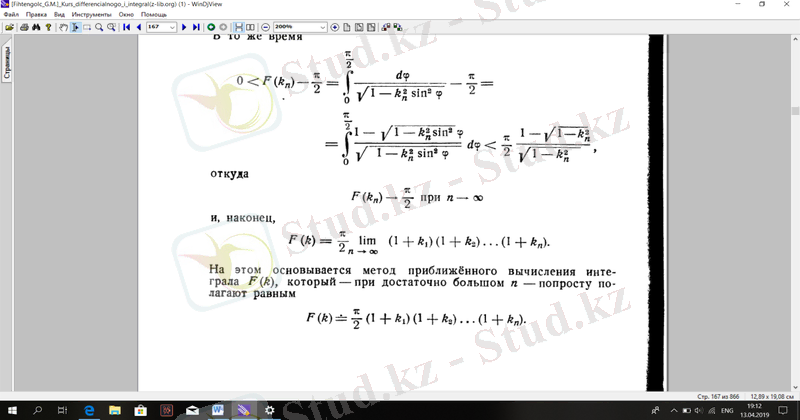
Қайдан

кезінде ақыр соңында Осыған F(k) интегралын жақындап есептеу әдісі негізделеді, ол - өте үлкен n -қарапайым тең деп қарастырылады

1. 2 Валлис Формуласы.

𝛑 𝟐 = 𝟐 𝟏 • 𝟐 𝟑 • 𝟒 𝟑 • 𝟒 𝟓 • 𝟔 𝟓 • 𝟔 𝟕 • • • • • • • • \frac{\mathbf{\pi}}{\mathbf{2}}\mathbf{=}\frac{\mathbf{2}}{\mathbf{1}}\mathbf{\bullet}\frac{\mathbf{2}}{\mathbf{3}}\mathbf{\bullet}\frac{\mathbf{4}}{\mathbf{3}}\mathbf{\bullet}\frac{\mathbf{4}}{\mathbf{5}}\mathbf{\bullet}\frac{\mathbf{6}}{\mathbf{5}}\mathbf{\bullet}\frac{\mathbf{6}}{\mathbf{7}}\mathbf{\bullet \bullet \bullet \bullet \bullet \bullet \bullet \bullet} (1)

𝛑 𝟐 = 𝐥𝐢𝐦 𝐧 → ∞ [ 𝟐 𝐧 ! ! ( 𝟐 𝐧 − 𝟏 ) ! ! ] 𝟐 • 𝟏 𝟐 𝐧 + 𝟏 \mathbf{\ \ }\frac{\mathbf{\pi}}{\mathbf{2}}\mathbf{=}\underset{\mathbf{n \rightarrow \infty}}{\mathbf{\lim}}{\left\lbrack \frac{\mathbf{2n!!}}{\left( \mathbf{2}\mathbf{n}\mathbf{- 1} \right) \mathbf{!!}} \right\rbrack^{\mathbf{2}}\mathbf{\bullet}\frac{\mathbf{1}}{\mathbf{2n + 1}}} (2)

Интегралмен дәлелдеу. Келесіні белгілейік: 𝐈 ( 𝐧 ) = ∫ 𝟎 𝛑 𝐬 𝐢 𝐧 𝐧 𝐱 𝐝 𝐱 \mathbf{I(n) =}\int_{\mathbf{0}}^{\mathbf{\pi}}{{\mathbf{si}\mathbf{n}^{\mathbf{n}}}\mathbf{xdx}} (1)

(Валлис интегралдары түрі) . Бөліктеп интегралдасақ

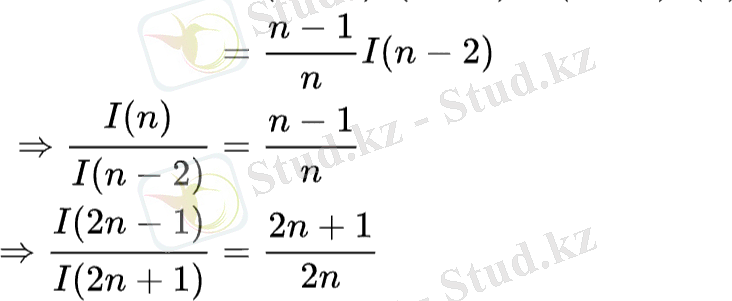
Бұл нәтиже төменде қолданылады:

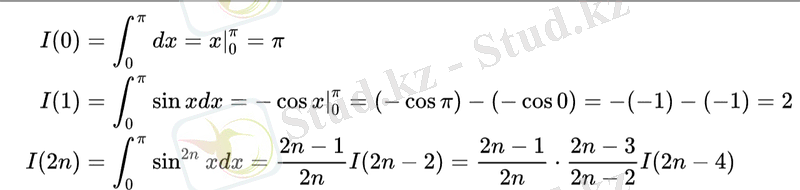
Процесті қайталаса

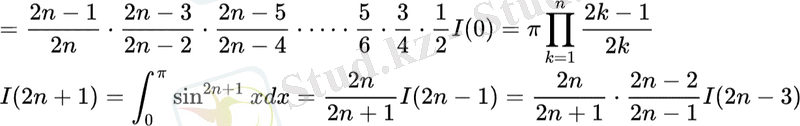
Процесті қайталаса

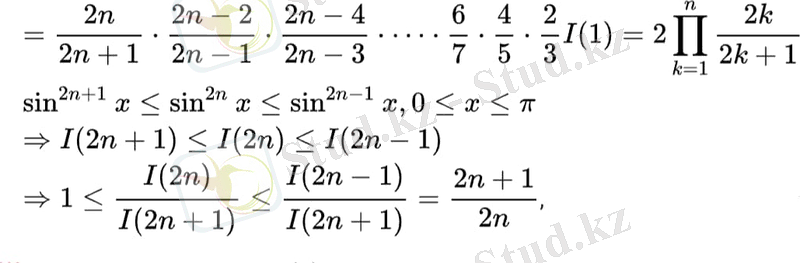
жоғарыдағы нәтиже бойынша. Жинақталу теоремасы негізінде,

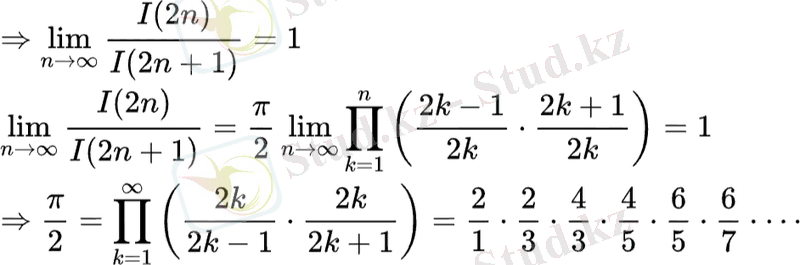
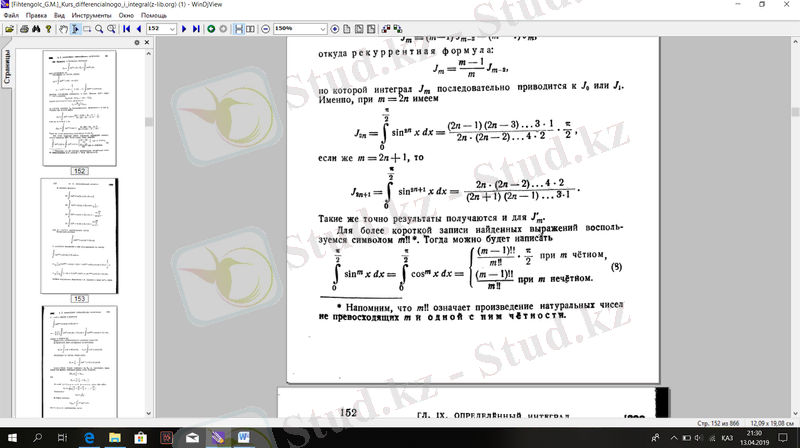(2)

n° формуласынан шығару оңай Валлистің атақты формуласы

Болжай отырып 0 < 𝐱 < 𝛑 𝟐 \mathbf{< x <}\frac{\mathbf{\pi}}{\mathbf{2}}\mathbf{\ } , 𝐬𝐢𝐧 𝐱 𝟐 𝐧 + 𝟏 < 𝐬𝐢𝐧 𝐱 𝟐 𝐧 < 𝐬𝐢𝐧 𝐱 𝟐 𝐧 − 𝟏 {\mathbf{\sin}\mathbf{x}}^{\mathbf{2n + 1}}\mathbf{<}{\mathbf{\sin}\mathbf{x}}^{\mathbf{2n}}\mathbf{<}{\mathbf{\sin}\mathbf{x}}^{\mathbf{2n - 1}} теңсіздігі бар. Бұл теңсіздікті 0-ден π 2 \frac{\pi}{2} -ге дейінгі аралықта интеграциялаймыз :

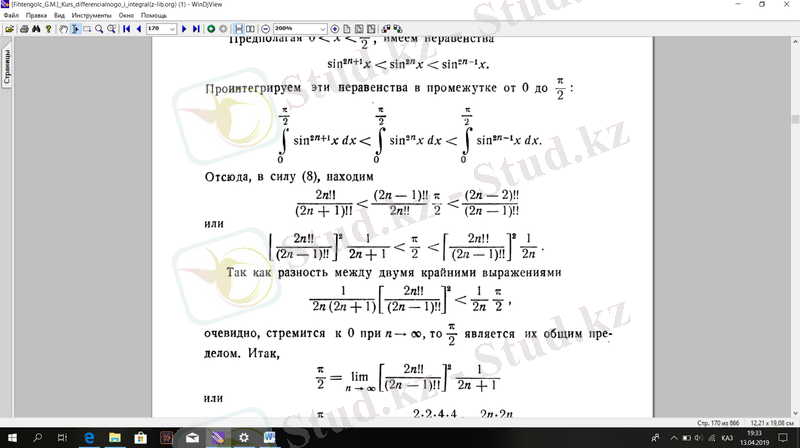
Демек біз

Немесе

Өйткені екі шеткі өрнектер арасындағы айырмашылық

кезінде 0 ұмтылады, онда π 2 \frac{\pi}{2\ }\ \ олардың жалпы шегі болып табылыды.

Сонымен,

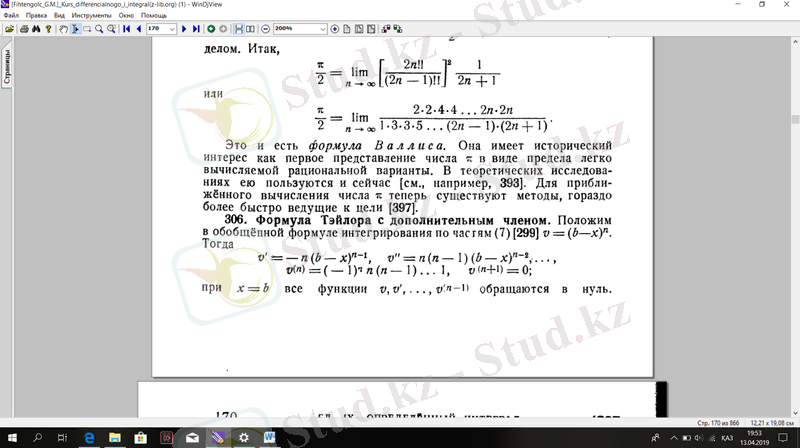
немесе

Бұл Валлис формуласы. Ол тарихи қызығушылық π \pi\ санының бірінші көрінісі ретінде шек түрінде оңай тиімді варианттарды есептеу. Теориялық тұрғыда оны қазір де пайдаланады .

3. 3 Санның трансценденттігі

Нақты сандарды рационалды және иррационалды деп бөлуден басқа, оларды алгебралық және транценденттік деп бөлу бар. Егер нақты Сан түр теңдеуін қанағаттандырса

𝐜 𝐧 𝐱 𝐧 + 𝐜 𝐧 − 𝟏 𝐱 𝐱 − 𝟏 + 𝐜 𝐧 − 𝟐 𝐱 𝐱 − 𝟐 + … + 𝐜 𝟐 𝐱 𝟐 + 𝐜 𝟏 𝐱 + 𝐜 𝟎 = 𝟎 \mathbf{c}_{\mathbf{n}}\mathbf{x}^{\mathbf{n}}\mathbf{+}\mathbf{c}_{\mathbf{n - 1}}\mathbf{x}^{\mathbf{x - 1}}\mathbf{+}\mathbf{c}_{\mathbf{n - 2}}\mathbf{x}^{\mathbf{x - 2}}\mathbf{+ \ldots +}\mathbf{c}_{\mathbf{2}}\mathbf{x}^{\mathbf{2}}\mathbf{+}\mathbf{c}_{\mathbf{1}}\mathbf{x +}\mathbf{c}_{\mathbf{0}}\mathbf{= 0}

онда біз бұл сан алгебралық деп айтамыз.

Трансценденттік сандардың мысалдары

  1. π\pi\саны.
  2. e Сан. (*)
  3. Кез келген табиғи санның ондық логарифмі10±n10^{\pm n}түрінің санынан басқа.
  4. sin⁡a, cos⁡aжәнеtan⁡a\sin{a, \ \ \ \cos{a\ және\ \tan a}}кез келген нөл емес алгебралық сандар үшін (Линдеман - Вейерштрасса теоремасы бойынша) .

Эрмиттің бір керемет теоремасын дәлелдеу үшін бастапқы пункт, е санына қатысты. (*)

Барлық заттай (сондай-ақ жалпы кешенді) сандар екі сыныпқа бөлінеді алгебралық және трансценденттік. Егер ол санның алгебралық түбірі болса, алгебралық деп аталады рационалды коэффициенттермен теңдеу (ортақтықты елемей, бұл коэффициенттер бүтін деп санауға болады) трансцендентті. Алгебралық санның мысалы кез келген ұтымды cан бола алады радикалдар арқылы көрінетін ло немесе иррационалдық cан: Сан - 11 17 \frac{11}{17} теңдеу түбірі 17х + 11 = 0, а сан 1 + 2 3 \sqrt{1 + \sqrt[3] {2}} түбірі

х 6 − 3 х 4 + 3 х 2 − 3 = 0 х^{6} - {3х}^{4} + {3х}^{2} - 3 = 0\ \ \ теңдеулері т. б.

Мысалы, e теңдеудің түбірі болып табылады

с 𝟎 + с 𝟏 е + с 𝟐 е 𝟐 + … + с 𝐦 𝐞 𝐦 = 𝟎 \mathbf{с}_{\mathbf{0}}\mathbf{+}\mathbf{с}_{\mathbf{1}}\mathbf{е +}\mathbf{с}_{\mathbf{2}}\mathbf{е}^{\mathbf{2}}\mathbf{+ \ldots +}\mathbf{с}_{\mathbf{m}}\mathbf{e}^{\mathbf{m}}\mathbf{= 0}

мұнда барлық коэффициенттер c 0 , c 1 , . . , c m − c_{0}, c_{1}, . ., c_{m} - \ бүтін сандар.

u=ƒ(x), ʋ= ( − 1 ) n + 1 e − x {( - 1) }^{n + 1}e^{- x}

формуласында еркін көпмүшелі болсын егер а = 0 алынса, бұл формула мына түрде болады

∫ 0 b f ( x ) e − x d x = − e − x ( f ( x ) + f ′ ( x ) + … + f ( n ) ( x ) ) \int_{0}^{b}{f(x) e^{- x}dx = - e^{- x}\ \left( f(x) + f'(x) + \ldots + f^{(n) }(x) \right) }

Сондықтан f ( n + 1 ) ( x ) = 0 . f^{(n + 1) }(x) = 0. \

Актілерінде қысқалық үшін

f ( x ) f(x) + f ′ ( x ) + … + f ( n ) ( x ) = F ( x ) , f'(x) + \ldots + f^{(n) }(x) = F(x),

бізде осында

e b F ( 0 ) = F ( b ) + e b ∫ 0 b f ( x ) e − x d x . e^{b}F(0) = F(b) + e^{b}\int_{0}^{b}{f(x) e^{- x}dx. }

Мұнда B = 0, 1, 2, тізбекті алыңыз . . . , m; көбейту алынатын

теңдік тиісінше c 1 , c 2 , c 3 , … , c m c_{1, }\ c_{2}, c_{3}, \ldots, c_{m}\ \ және түрлендіріп соңғы теңдікке келтіреміз

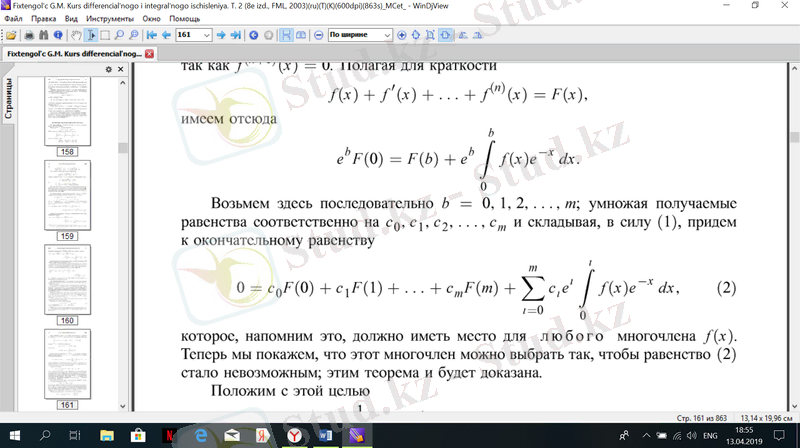
ол кез келген F(x) үшін орын алуы керек бұл теорема және дәлелденеді.

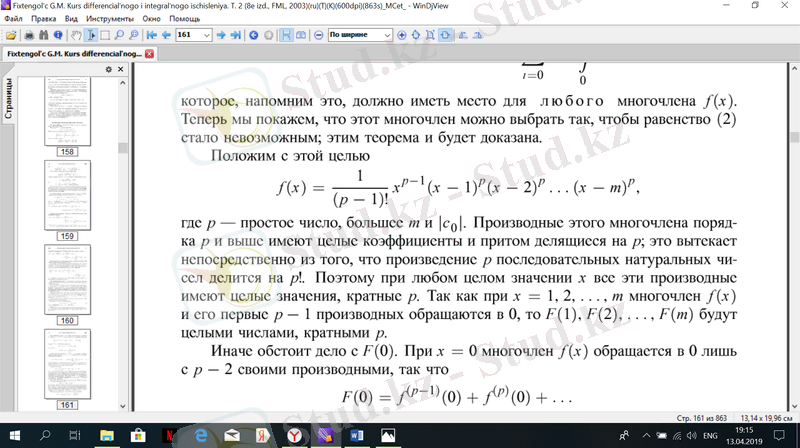
Изображение выглядит как снимок экрана Автоматически созданное описание

мұнда р-қарапайым cан, m және c 0 c_{0} . Бұл көптеген туындылар қатарынан және одан жоғары коэффициенттері бар және р-ға бөлінетін; бұл тікелей р дәйекті туындысы- ауылдарға бөлінеді. Сондықтан кез келген мәнде х барлық осы туындылар x = 1, 2 кезінде, өйткені көпжақты f (x) және оның алғашқы Р - 1 туындылары 0, онда F(l), FB) . . . , F (m) болады р еселік бүтін сандармен х = 0 кезінде F[x) 0-ге ғана жүгінеді P - 2 өз туындыларымен, сондықтан,

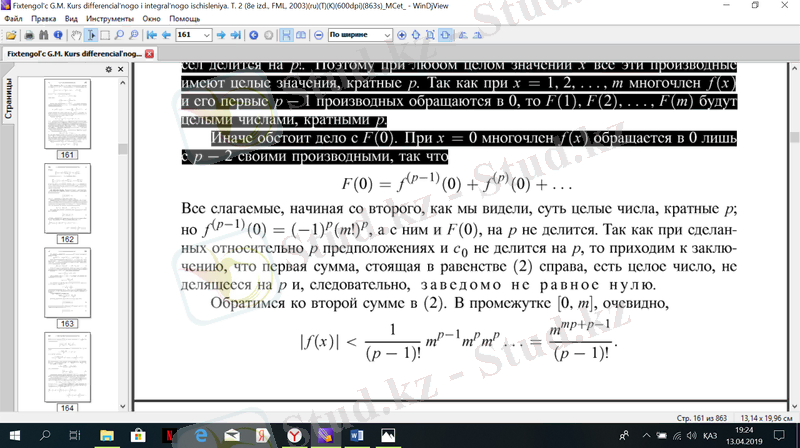
Изображение выглядит как снимок экрана Автоматически созданное описание

Біз көргеніміздей, екіншісінен бастап, барлық қосылымдар, мәні бүтін сандар, еселік;

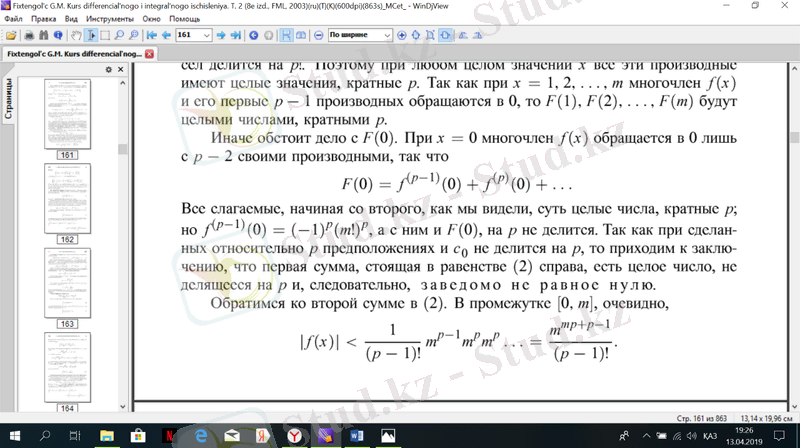
Изображение выглядит как снимок экрана Автоматически созданное описание

сонымен бірге F(0) бөлінбейді. Өйткені кезінде жасалды- және с 0-ге бөлінбейді, онда теңдікте тұрған бірінші сома оң жақта, бүтін сан бар, р-ға бөлінетін, демек, нөлге тең емес екенін бекітеміз.

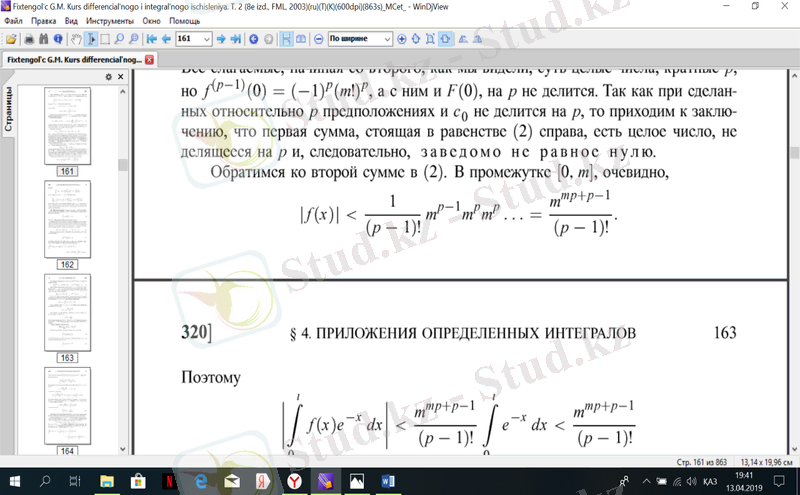
Изображение выглядит как снимок экрана Автоматически созданное описание

Сондықтан

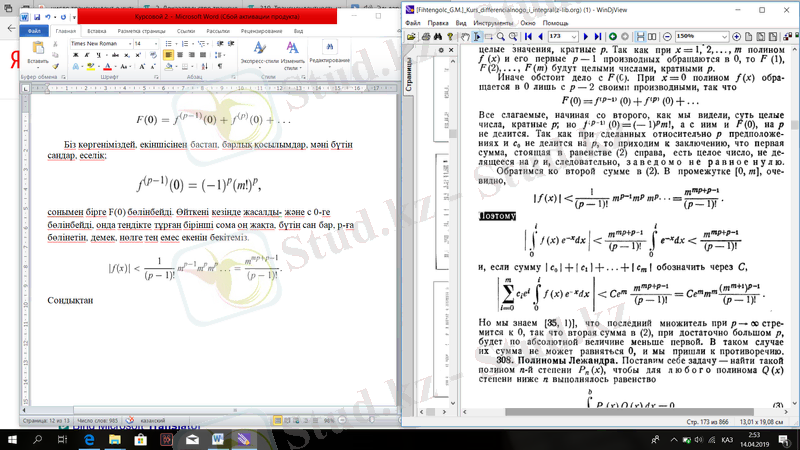
Және с 𝟎 + с 𝟏 + … + с 𝐦 \left \mathbf{с}_{\mathbf{0}} \right\mathbf{+}\left \mathbf{с}_{\mathbf{1}} \right\mathbf{+ \ldots +}\left \mathbf{с}_{\mathbf{m}} \right С арқылы белгілесе,

II. Практикалық бөлім

1. I = ∫ 0 π x cos ⁡ x d x I = \int_{0}^{\pi}{x{\cos x}{dx}} (1)

онда,

I = ∫ 0 π x d s i n x = [ x sin x ] 0 π − ∫ 0 π sin ⁡ x d x = [ cos x ] 0 π = − 2 I = \int_{0}^{\pi}{x{dsin}{x = \left\lbrack x\sin x \right\rbrack_{0}^{\pi} - \int_{0}^{\pi}{\sin{xdx = \left\lbrack \cos x \right\rbrack_{0}^{\pi} = - 2 (2)

Валлис формуласы

Алдыңғы тармақтардың нәтижелері арқылы π \pi\ санына арналған өрнектерді шығаруға болады. \

U = ∫ 0 π 2 cos ⁡ x n d x , \ \ \ \ U = \int_{0}^{\frac{\pi}{2}}{{\cos x}^{n}{dx}, } (3)

интегралды қарастырайық мұнда n-бүтін және теріс емес сан.

U 0 = π 2 , U 1 = 1 U_{0} = \frac{\pi}{2}, \ \ U_{1} = 1 (4)

Енді n > 1 деп болжаймыз. Содан кейін бөліктеп интегралдаймыз:

U n = ∫ 0 π 2 cos ⁡ x n − 1 d sin ⁡ x = [ sin x cos ⁡ x n − 1 ] 0 π 2 − ∫ 0 π 2 sin ⁡ x d ( cos ⁡ x n − 1 ) U_{n} = \int_{0}^{\frac{\pi}{2}}{{\cos x}^{n - 1}d\sin x = \left\lbrack \sin x{\cos x}^{n - 1} \right\rbrack_{0}^{\frac{\pi}{2}}} - \int_{0}^{\frac{\pi}{2}}{\sin xd\left( {\cos x}^{n - 1} \right) } (5)

Өйткені оң бөліктің бірінші мүшесі нөлге тең, онда

U n = ( n − 1 ) ∫ 0 π 2 cos ⁡ x n − 2 sin ⁡ x 2 d x = ( n − 1 ) ∫ 0 π 2 cos ⁡ x n − 2 ( 1 − cos ⁡ x 2 ) d x U_{n} = (n - 1) \int_{0}^{\frac{\pi}{2}}{{\cos x}^{n - 2}{\sin x}^{2}dx = (n - 1) \int_{0}^{\frac{\pi}{2}}{{\cos x}^{n - 2}(1 - {\cos x}^{2}) {dx}}} (6)

Осыдан

U n − 2 = ( n − 1 ) ( U n − 2 − U n ) U_{n - 2} = (n - 1) \left( U_{n - 2} - U_{n} \right) (7)

Онда,

U n = n − 3 n − 2 U n − 4 {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ U}_{n} = \frac{n - 3}{n - 2}U_{n - 4} (8)

Осылайша,

U 3 = 2 3 U 1 {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ U}_{3} = \frac{2}{3}U_{1} (9)

теңдікке келгенге дейін жалғастыруға болады. U n U_{n\ \ } арқылы U n − 2 U_{n - 2\ \ } , содан кейін U n − 2 U_{n - 2\ \ } арқылы U n − 4 U_{n - 4\ \ } және т . б., аламыз:

U n = 2 • 3 • 4 • ( n − 1 ) 3 • 4 • 5 • n • U 1 {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ U}_{n} = \frac{2 \bullet 3 \bullet 4 \bullet (n - 1) }{3 \bullet 4 \bullet 5 \bullet n} \bullet U_{1} (10)

U 1 = 1 U_{1} = 1\ және m аспайтын және m бірдей анық бар барлық табиғи сандардың көбейтіндісін белгілей отырып, m ! ! , \ m!!, \ арқылы

U n = ( n − 1 ) ! ! n ! ! {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ U}_{n} = \frac{(n - 1) !!}{n!!} (11)

табамыз. Жұп n үшін ұқсас:

U n = ( n − 1 ) ! ! n ! ! • π 2 {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ U}_{n} = \frac{(n - 1) !!}{n!!} \bullet \frac{\pi}{2} (12)

Бұл теңдікті орнату арқылы 0 ≤ x ≤ π 2 0 \leq x \leq \frac{\pi}{2}\ болады

cos2 n +2 x ≤ cos2 n +1 x ≤ cos2 n x , (*) сүйене отырып, қайдан табуға болады:

U 2n+2 < U 2n+1 < U 2n (13)

(*) Егер a ≤ b, f(x) және u·g(x) - [a, b] - те f(x) ≤ g(x) шартын қанағаттандыратын екі үздіксіз функция болса, онда:

∫ a b f ( x ) d x ≤ ∫ a b g ( x ) d x \int_{a}^{b}{f{(x) dx} \leq \int_{a}^{b}{g(x) }{dx}} (*1)

яғни интегралдау шектерінің қалыпты тәртібінде теңсіздікті біріктіруге болады. Шын мәнінде,

... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
ГАУСС ФОРМУЛАСЫ
Математиктердің бекзадасы Карл Фридрих Гаусс
XIII ғасырға дейінгі Еуропа математикасы
Мектеп математикасының тарихи мағлұматтары
Кеңістіктегі вектор
Есептеу математикасына кіріспе пәні бойынша оқу-әдістемелік кешен
МАТЕМАТИКА ЖӘНЕ ЭЙЛЕР
Ньютон формуласы
Сызықты емес теңдеулер жүйесін шешудің сандық әдістері
Түйіндес түрлендірулер
Пәндер

Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.

google play appstore

instagram tiktok

Ақпарат

Қосымша


Email: info@stud.kz



Реферат Курстық жұмыс Диплом Материал Диссертация Практика Презентация Сабақ жоспары Мақал-мәтелдер 1‑10 бет 11‑20 бет 21‑30 бет 31‑60 бет 61+ бет Негізгі Бет саны Қосымша Іздеу Ештеңе табылмады :( Соңғы қаралған жұмыстар Қаралған жұмыстар табылмады Тапсырыс Антиплагиат Қаралған жұмыстар kz