Теңдеулер мен теңсіздіктер: жіктелуі және шешу әдістері


ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
ОҢТҮСТІК ҚАЗАҚСТАН МЕМЛЕКЕТТІК ПЕДАГОГИКАЛЫҚ УНИВЕРСИТЕТІ
РЕФЕРАТ
Тақырыбы: Теңдеулер мен теңсіздіктер және оларды шығару тәсілдері.
Орындаған:Ауесханов Н.
Тобы:109-26А
Қабылдаған:Ибрагимов Р.
Жоспар
- Кіріспе
- Негізгі бөлім1. Квадраттық теңдеулерді шешу.
2. Иррационал теңдеулерді шешу.
III. Қорытынды.
IV. Пайдаланылған әдебиеттер.
Құрамында әріппен белгілеген белгісізі (айнымалысы) бар теңдік теңдеу деп аталады. Мысалы: 5х + 8 = 18; 6х + 7 = -5; 3(х + 7) = 15 - теңдеулер, х - белгісіз. Мұндай теңдеулерді бір белгісізі бар немесе бір айнымалысы бар теңдеулер деп атайды.
Теңдеудің оң жағы және сол жағы болады. Мысалы:4х +17 = 19 теңдеуіндегі (4х +17) - теңдеудің сол жағы, ал 19 оң жағы. Теңдеудегі алгебралық қосылғыштардың әрқайсысы оның мүшелері деп аталады. Мұндағы 4х - белгісізі бар мүше, 7, 9 - бос мүшелер.
Теңдеумен берілген мысалдар мен есептерді шығарғанда, ондағы әріппен берілген белгісіздің немесе айнымалының сан мәнін табамыз. Демек, теңдеудің түбірін табамыз.
Белгісіз санның немесе айнымалының теңдеуді тура санды теңдікке айналдырытын мәні теңдеудің түбірі деп аталады.
Теңдеудің шешімі дегеніміз - оның түбірлерін табу немесе түбірлерінің жоқ екенін дәлелдеу. Теңдеулерді шешкенде, кейде түбірлері бірдей болатын теңдеулерді мәндес теңдеулер деп айтады. Мысалы, 2х = 10 теңдеуі мен 3х = 15 және3х -х = 2, 5 ∙ 4 теңдеулері мәндес теңдеулер, түбірлері бірдей х = 5.
Ескеретін жағдай, кейде теңдеулердің түбірі болмайды. Түбірлері болмайтын теңдеулерде мәндес теңдеулер болып саналады.
Теңдеу - әрпі бар теңдік болғандықтан, теңдеудің қасиеттерін теңдіктің қасиеттеріне сүйеніп дәлелдейміз.
Теңдеулер
Алгебралық теңдеулер
Трансценденттік теңдеулер
Иррационал теңдеулер
Рационал теңдеулер
Бүтін теңдеулер
Бөлшек-рационал теңдеулер
Квадрат теңдеулер
Жоғары дәрежелі теңдеулер
Сызықтық теңдеулер
Тригонометриялық теңдеулер
Көрсеткіштік теңдеулер
Логарифмдік теңдеулер
Квадрат теңдеудің анықтамасы.
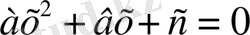 (1)
түрінде берілген теңдеу
квадрат теңдеу
деп аталады.
(1)
түрінде берілген теңдеу
квадрат теңдеу
деп аталады.
Мұндағы а, в, с нақты сандар.
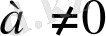 , х-айнымалы.
, х-айнымалы.
а - бірінші коэффициент, в - екінші коэффициент, с- бос мүше.
Егер (1) теңдеудегі
 болса, онда ол теңдеу толық
квадрат теңдеу
деп аталады. Іс жүзінде кездесетін көптеген есептерді шешу, мысалы 2
болса, онда ол теңдеу толық
квадрат теңдеу
деп аталады. Іс жүзінде кездесетін көптеген есептерді шешу, мысалы 2
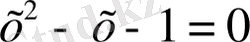 , 3
, 3
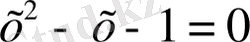 түрдегі мысалдарды алуға болады.
түрдегі мысалдарды алуға болады.
Толымсыз квадрат теңдеулер
Егер ах 2 +вх+с=0 түріндегі теңдеудің в немесе с, немесе в мен с нөлге тең болатын дербес жағдайлардағы квадрат теңдеу толымсыз квадрат теңдеу деп аталады.
Толымсыз квадрат теңдеулер былай жазылады.
1.
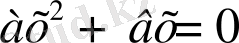 , мұндағы с=0.
, мұндағы с=0.
2.
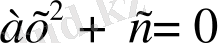 , мұндағы в=0.
, мұндағы в=0.
3.
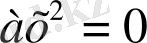 , мұндағы в=0, с=0. Мысалы: 2 х
2
= 0
, в
=с=0,
х
2
+ х - 7 = 0, в
=0 және
, мұндағы в=0, с=0. Мысалы: 2 х
2
= 0
, в
=с=0,
х
2
+ х - 7 = 0, в
=0 және
х 2 + 6х = 0, с =0
Квадрат теңдеуді шешудің ӘДІСТЕРІ
1-әдіс. Теңдеудің сол жақ бөлігін көбейткіштерге жіктеу.
х 2 + 10х - 24 = 0 теңдеуді жіктейміз .
Теңдеудің сол жақ бөлігін көбейткіштерге жіктейміз:
х 2 + 10х - 24 = х 2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12) (х - 2) .
Демек, теңдеуді былай жазуға болады:
(х + 12) (х - 2) = 0
Көбейтінді нөлге тең болғандықтан, ең болмағанда көбейткіштердің біреуі нөлге тең болуы керек. Сондықтан теңдеулердің сол жақ бөлігіндегі х = 2 және х = - 12 сандары х 2 + 10х - 24 = 0 теңдеуінің түбірлері болып табылады.
2-әдіс. Толық квадратқа келтіру әдісі.
Мысал: х 2 + 6х - 7 = 0 теңдеуін шешейік.
Сол жақ бөлігін толық квадратқа келтіреміз. Ол үшін х 2 + 6х өрнегін төмендегідей жазып аламыз:
х 2 + 6х = х 2 + 2• х • 3.
Алынған өрнектің бірінші қосындысы х-тың квадраты, ал екінші қосындысы х пен 3-тің екі еселенгені. Толық квадрат алу үшін 3 2 -ын қосу керек. Сонда
х 2 + 2• х • 3 + 3 2 = (х + 3) 2 .
Енді теңдеудің сол жағын түрлендіреміз. Берілген теңдеуге 3 2 -ын қосып, алып тастаймыз. Сонда шығатыны:
х 2 + 6х - 7 = х 2 + 2• х • 3 + 3 2 - 3 2 - 7 = (х + 3) 2 - 9 - 7 = (х + 3) 2 - 16.
Сонымен, берілген теңдеуді былайша жазуға болады:
(х + 3) 2 - 16 =0, (х + 3) 2 = 16.
Бұдан, х + 3 - 4 = 0, х 1 = 1, немесе х + 3 = -4, х 2 = -7.
3-әдіс. Квадраттық теңдеулерді формула арқылы шешу.
ах 2 + bх + с = 0, а ≠ 0
теңдеудің екі жағын да 4а-ға көбейтеміз де, төмендегі өрнекті аламыз:
4а 2 х 2 + 4аbх + 4ас = 0,
((2ах) 2 + 2ах • b + b 2 ) - b 2 + 4ac = 0,
(2ax + b) 2 = b 2 - 4ac,
2ax + b = ± √ b 2 - 4ac,
2ax = - b ± √ b 2 - 4ac,
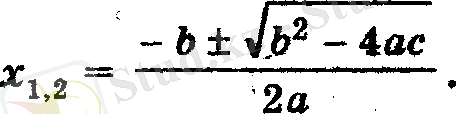
Оған келесідегідей мысалдар келтіруге болады: 4х 2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b 2 - 4ac = 7 2 - 4 • 4 • 3 = 49 - 48 = 1,
Д>0 болғандықтан, екі әр түрлі түбір болады:
Сонымен, дискриминант оң болғанда, яғни в 2 -4ас>0, ах 2 +вх+с=0 теңдеуінің екі түрлі түбірі болады.
б) 4х 2 - 4х + 1 = 0, теңдеуін шешейік.
а = 4, b = - 4, с = 1, D = b 2 - 4ac = (-4) 2 - 4 • 4 • 1= 16 - 16 = 0,
D = 0, болғандықтан, бір ғана түбір бар болады

Сонымен, егер дискриминант нөлге тең болса, b 2 - 4ac = 0 , то уравнение
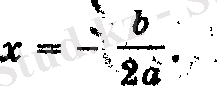 ах
2
+ bх + с = 0
теңдеуінің жалғыз түбірі бар болады
ах
2
+ bх + с = 0
теңдеуінің жалғыз түбірі бар болады
в) 2х 2 + 3х + 4 = 0, теңдеуін шешейік.
а = 2, b = 3, с = 4, D = b 2 - 4ac = 3 2 - 4 • 2 • 4 = 9 - 32 = - 13, D < 0.
Д<0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды. .
Д<0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды. b 2 - 4ac < 0 онда ах 2 + bх + с = 0 теңдеуінің түбірі болмайды
4-әдіс. Виет теоремасын пайдаланып теңдеулерді шешу
Келтірілген түбірлері Виет теоремасын қанағаттандырады. Ол былай беріледі: х 2 + px + c = 0. (1) а=1 болғанда, x 1 x 2 = q, x 1 + x 2 = - p
Бұдан келесі тұжырымдарды шығаруға болады: а) Егер q (1) теңдеудің бос мүшесі оң болса (q0) онда теңдеудің екі бірдей таңбалы түбірі болады. Егер р>0, онда екі түбірі де теріс болады, егер р<0, онда түбірлері оң болады.
Мысал, x 2 - 3x + 2 = 0; x 1 = 2 және x 2 = 1, мұнда q = 2 > 0 , p = - 3 < 0;
x 2 + 8x + 7 = 0; x 1 = - 7 және x 2 = - 1, мұнда q = 7 > 0 , p= 8 > 0.
б) Егер q (1) теңдеудің бос мүшесі теріс болса (q <0), онда теңдеудің екі түрлі, таңбалы екі түбірі болады, түбірдің модулі бойынша үлкені оң болады, егер р <0 болса, теріс болады, егер р >0.
Мысал:
x 2 + 4x - 5 = 0; x 1 = - 5 , x 2 = 1, м ұнда q= - 5 < 0 , p = 4 > 0;
x 2 - 8x - 9 = 0; x 1 = 9 и x 2 = - 1, мұнда q = - 9 < 0, p = - 8 < 0.
5-әдіс. Теңдеуді «асыра лақтыру» әдісімен шешу
ах 2 + bх + с = 0, а ≠ 0 . квадрат теңдеуін қарастырамыз. Теңдеудің екі жағын да а-ға көбейтіп, мынаны аламыз:
а 2 х 2 + аbх + ас = 0. . ах = у деп белгілесек, х = у/а
Олай болса у 2 + by + ас = 0, еңдеуіне келеміз. Бұл бастапқы теңдеумен тең. Теңдеудің түбірлерін у 1 , у 2 -ні Виет теоремасы арқылы табамыз.
Соңында х 1 = у 1 /а , х 1 = у 2 /а -ны аламыз. Бұл жағдайда а коэффициентін бос мүшеге көбейтеді. Сондықтан да бұл әдісті «асыра лақтыру» әдісі деп атайды . Бұл әдісті көбінесе Виет теоремасын пайдаланып түбірді оңай табуда және дискриминант дәл квадрат болғанда қолданады.
мысалы, 2х 2 - 11х + 15 = 0 теңдеуін шешейік.
Шешуі: 2 коэффициенті теңдеудің бос мүшесіне асыра лақтырамыз, нәтижесінде: у 2 - 11у + 30 = 0. Виет теоремасы бойынша
у 1 = 5 х 1 = 5/2 x 1 = 2, 5
у 2 = 6 x 2 = 6/2 x 2 = 3.
Жауабы: 2, 5; 3.
6-әдіс. Квадрат теңдеулердің коэффициенттерінің қасиеттерін қолдану.
ах 2 + bх + с = 0, , а ≠ 0 квадрат теңдеуі берілген.
1) Егер, а+ b + с = 0 (яғни коэффициенттер қосындысы 0-ге тең) болса, онда х 1 = 1,
х 2 = с/а.
Дәлелдеу: а ≠ 0, келесідей квадрат теңдеуге келеміз.
x 2 + b/a • x + c/a = 0.
Виет теоремасы арқылы
x 1 + x 2 = - b/a,
x 1 x 2 = 1• c/a.
а - b + с = 0 шарты бойынша, b = а + с аламыз. Олай болса,
x 1 + x 2 = - а + b/a= -1 - c/a,
x 1 x 2 = - 1• ( - c/a),
х 1 = -1 , х 2 = c/a болатынын дәлелдндік.
- Мысал:345х2- 137х - 208 = 0теңдеуін шешейік.
Шешуі. а + b + с = 0 (345 - 137 - 208 = 0),
онда
х 1 = 1, х 2 = c/a = -208/345.
Жауабы: 1; -208/345.
2) 132х 2 - 247х + 115 = 0 теңдеуін шешейік.
Шешуі. а + b + с = 0 (132 - 247 + 115 = 0),
онда
х 1 = 1, х 2 = c/a = 115/132.
Жауабы: 1; 115/132.
7-әдіс Квадрат теңдеуді шешудің графиктік түрі
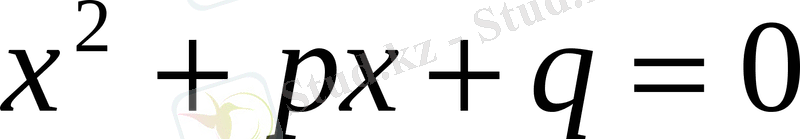 теңдеуінен екінші, үшінші мүшелерін оң жағына шығарсақ,
теңдеуінен екінші, үшінші мүшелерін оң жағына шығарсақ,
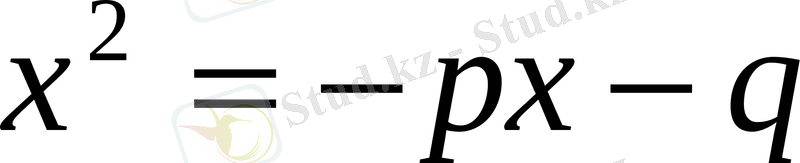 аламыз.
аламыз.
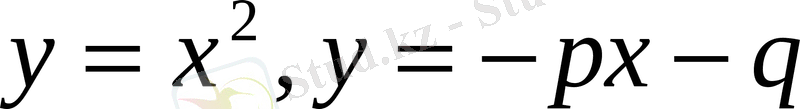 тұрғызамыз.
тұрғызамыз.
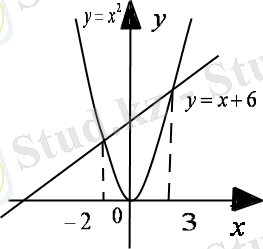
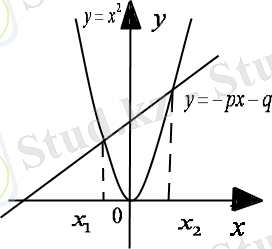 Бірінші функцияның графигі - координат басынан өтетін парабола, екінші функцияның графигі - түзу (1-сурет) . Енді келесі жағдайлар болуы мүмкін:
Бірінші функцияның графигі - координат басынан өтетін парабола, екінші функцияның графигі - түзу (1-сурет) . Енді келесі жағдайлар болуы мүмкін:
-түзу және парабола екі нүктеде қиылысуы мүмкін, қиылысу нүктесінің абциссасы квадрат теңдеудің түбірі болады.
- түзу және парабола жанасуы мүмкін (бір ғана ортақ нүктеде), яғни теңдеудің бір ғана шешімі болады.
-парабола және түзудің ортақ нүктелері жоқ, яғни теңдеудің түбірі жоқ.
Мысал:
1)

 теңдеуін графиктік тәсілмен шешеміз.
теңдеуін графиктік тәсілмен шешеміз.
Шешуі:
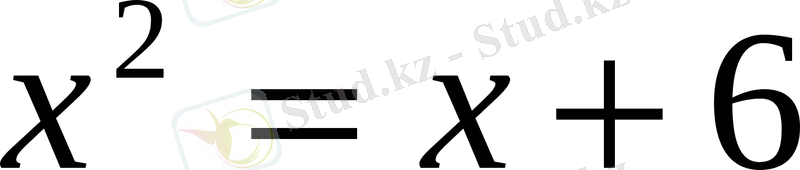 түрінде жазамыз.
түрінде жазамыз.
 параболасын және
параболасын және
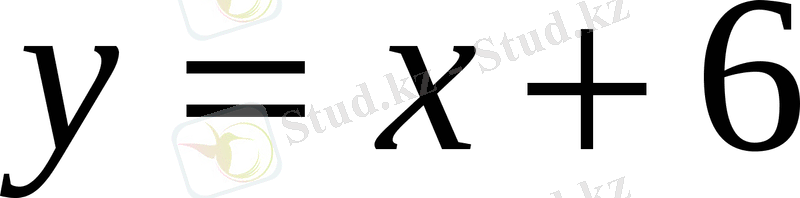 түзуін тұрғызайық.
түзуін тұрғызайық.
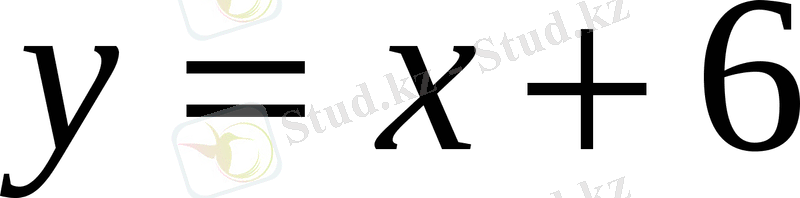 түзуін мына М(0, 6) және N(3, 9) нүктелері арқылы тұрғызуға болады. Түзу және парабола А, В нүктелері абсциссалары
түзуін мына М(0, 6) және N(3, 9) нүктелері арқылы тұрғызуға болады. Түзу және парабола А, В нүктелері абсциссалары
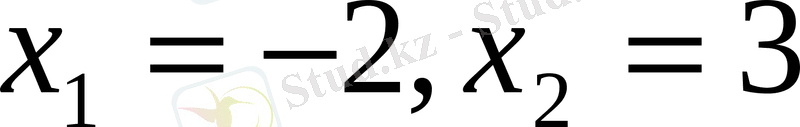 -пен қиылысады.
-пен қиылысады.
Жауабы:
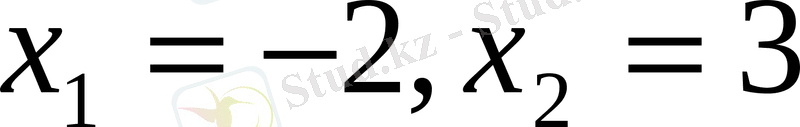
2)
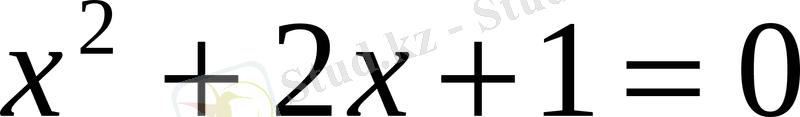 теңдеуін графиктік тәсілмен шешеміз
теңдеуін графиктік тәсілмен шешеміз
Шешуі:
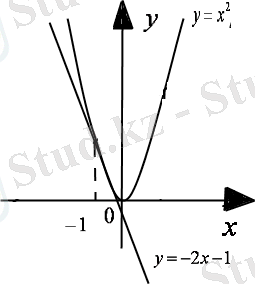
 түрінде жазамыз. y=х
2
параболасын және у=-2х-1 түзуін тұрғызайық. у=-2х-1 түзуін М(0; -1) және N(
түрінде жазамыз. y=х
2
параболасын және у=-2х-1 түзуін тұрғызайық. у=-2х-1 түзуін М(0; -1) және N(
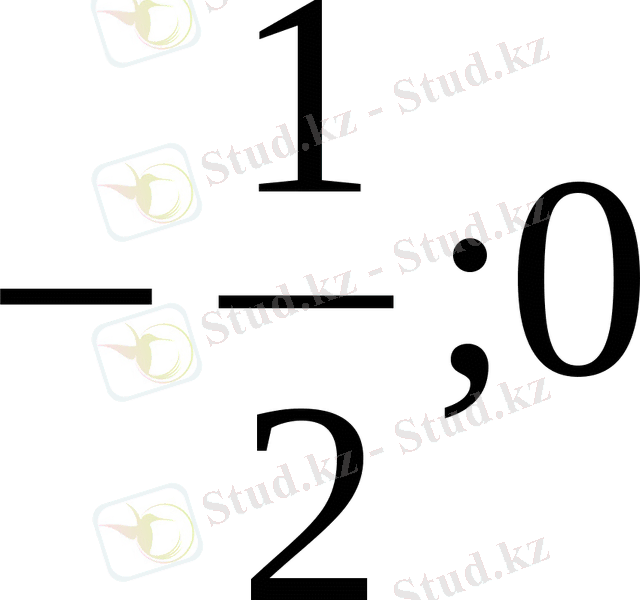 ) нүктелері арқылы жүргіземіз. Парабола мен түзу А нүктесінде қиылысады, абциссасы х=-1 тең.
) нүктелері арқылы жүргіземіз. Парабола мен түзу А нүктесінде қиылысады, абциссасы х=-1 тең.
Жауабы:
х=-1
Иррационал теңдеу
Иррационал теңдеу
- белгісізі, яғни айнымалы шамасы радикал таңбасының астында болатын теңдеу, мысалы,
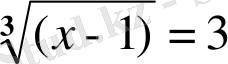 {\displaystyle ~3{\sqrt {\left(x-1\right) }}=3. }
{\displaystyle ~3{\sqrt {\left(x-1\right) }}=3. }
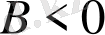
Мұны шешу үшін тендеудің екі жағын үшінші дәрежеге шығарамыз, сонда
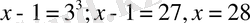 {\displaystyle ~x-1=3^{3}; x-1=27, x=28}
{\displaystyle ~x-1=3^{3}; x-1=27, x=28}
Иррационал теңдеулерді әдетте радикалдардан арылту тәсілімен шешеді. Бұл үшін тендеудің екі жақ бөлігінде тендеу рационал өрнек пайда болатындай тәсілмен дәрежелеу керек. Кейде бұл жайтты бірнеше рет қайталауға тура келеді. Осы түрлендірулер нәтижесінде алгебралық теңдеу (бүтін немесе бөлшек), жалпы алғанда, бастапқы берілген теңдеуге мәндес (эквивалентті) болмай қалады. Көбінесе берілген теңдеудің салдары пайда болады. Тендеуді канағаттандырмайтын шешімдібөгде шешім ретінде ескермейтін боламыз. Бірақ та теңдеудің екі жақ бөлігі тақ дәрежеге дәрежеленген болса, онда жаңа теңдеу бастапқы теңдеуге мәндес (эквивалентті) болады. Мына тендеулер жүбы мәндес болмайды:
- {\displaystyle ~{\sqrt {A}}={\sqrt {B}}}және {\displaystyle ~A=B}:
- {\displaystyle ~{\sqrt {A}}\cdot {\sqrt {B}}=C}және {\displaystyle ~{\sqrt {AB}}=C};
- {\displaystyle ~{\dfrac {\sqrt {A}}{\sqrt {B}}}=C}және {\displaystyle ~{\sqrt {\dfrac {A}{B}}}=C};
Осы өрнектердің оң жағындағы теңдеулерінің бір мезгілде {\displaystyle ~A<0}
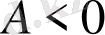 және {\displaystyle ~B<0}
және {\displaystyle ~B<0}
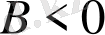 болған жағдайдағы шешімдері сол жақгағы тендеулердің шешімдері болмайды.
болған жағдайдағы шешімдері сол жақгағы тендеулердің шешімдері болмайды.
1.
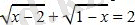 теңдеуін шешіңіз.
теңдеуін шешіңіз.
Шешуі. Бұл теңдеуді екі жағын да квадраттау немесе теңдеулер жүйесіне келтіру әдістерімен шешуге болады. Осы әдістердің әрқайсысы да біршама есептеулер жүргізуді қажет етеді. Күрделі есептеулерсіз теңдеудің шешімін анықтауға мүмкіндік беретін әдісті қарастырайык. Осы мақсатта, функцияның анықталу облысын табамыз. Ол келесі теңсіздіктер жүйесінің шешімі:
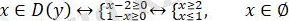
Яғни,
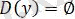 теңдеудің шешімі жоқ.
теңдеудің шешімі жоқ.
Кейде анықталу облысы ақырлы нүктелер жиынынан тұрады, ондай жағдайда теңдеудің шешімі больш табылатындарын олардың арасынан тексеріп, таңдау ғана жеткілікті. Ал кей жағдайларда анықталу облысы ақырлы нүктелер жиынынан тұрмайды, сондыктан біp қарағанда, теңдеу анықталу облысын зерттеу жолымен шешілмейтін болып көрінеді. Бірақ анықталу облысын табу тәсілін теңдеуді шешудің әр қадамында қолдануға болады.
2.
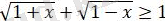 теңсіздігін шешіңіз.
теңсіздігін шешіңіз.
Шешуі.
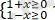 теңсіздіктер жүйесінің шешімі -1≤ х≤ 1 екендігін көру қиын емес. Яғни, берілген өрнектің анықталу облысы -1≤ х≤ 1
теңсіздіктер жүйесінің шешімі -1≤ х≤ 1 екендігін көру қиын емес. Яғни, берілген өрнектің анықталу облысы -1≤ х≤ 1
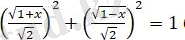 болғандықтан,
болғандықтан,
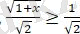 немесе
немесе
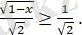
Сондықтан,
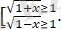 . Онда
. Онда
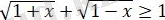 теңсіздігі анықталу облысына тиісті барлық
x
үшін орындалады. Демек
теңсіздігі анықталу облысына тиісті барлық
x
үшін орындалады. Демек
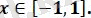
3.
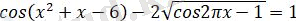 тендеуін жүйесін шешіңіз.
тендеуін жүйесін шешіңіз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz