Эйлердің қозғалыс дифференциалды теңдеуі

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

Баяндама

«Эйлердің қозғалыс дифференциалды теңдеуі»

Орындаған:

Қабылдаған:

Қарағанды

2019-2020 оқу жылы

Эйлердің қозғалыс дифференциалды теңдеуі

Сұйық қозғалыстарының түрлерін зерттей келе, жылдамдық пен қысымның кеңістік координаталарындағы бөлшек пен уақыттың жағдайына функционалды тәуелділігін орнатуға болады.

Ағу шарттарына байланысты сұйық қозғалысы қалыптасқан және қалыптаспаған болып бөлінеді. Қалыптасқан қозғалыс біркелкі және біркелкі емес, сондай-ақ тегеурінді және тегеурінсіз және баяуөзгеретін деп ажыратуға болады.

Ішкі күштер әсерінен сұйықтың қозғалыс заңдылықтарын оқығанда, ағыстың ағыншалы құрылымы туралы түсінік пайда болады. Кез-келген ағын жеке, бір-бірімен өзара араласпайтын ағыншалардан ешқандай бос орын қалдырмай сұйықтың барлық көлемін толтырады деп болжанады. Сұйықтың кез-келген ағыны мынадай негізгі параметрлермен сипатталуы мүмкін: ағынның тірі қимасы ; сұйықтану периметрі ; гидравликалық радиус ; ағыстың орташа жылдамдығы , сұйық шығыны .

Шығын деп бірлік уақытта көлденен қима арқылы ағып өткен сұйық мөлшерін айтамыз. Шығын көлем, салмақ немесе масса бірлігінде өлшенуі мүмкін. Осыған сәйкес шығындарды бөледі: көлемдік, салмақтық немесе массалық.

Қалыптасқан қозғалыста қозғалыс жылдамдығының шамасы мен бағыты уақыт бойынша өзгермейді, сұйықтың қозғалысы тек кеңістіктің координаталарына ғана байланысты өзгереді және кез-келген нүктеде уақыт бойынша өзгермейді.

Сұйық құбырмен қалыптасқан қозғалыста ақса, онда құбырдың әрбір көлденең қимасынан уақыт бірлігінде өткен сұйықтың мөлшері тұрақты болады, оны келесі теңдеу арқылы анықтаймыз

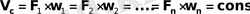
Көрсетілген теңдеу көлемдік шығынның тұрақтылық теңдеуі деп аталады немесе ағын үшін қозғалыстың үзіліссіздік теңдеуі деп аталады. Осы теңдіктен тірі қимадағы орташа жылдамдық оның ауданына кері пропорционалды екенін көруге болады.

Жалпы жағдайда, идеалды сұйықтың қозғалыс сипаттамалары үшін Даламбер принципін қолдануға болады, сонда қарастырылатын жүйеге әсер ететін күштер инерция күштері арқылы қалыпқа келеді.

Бұл принциптің аналитикалық мәні мынада, барлық күштердің қосынды проекциялары, соның ішінде инерция күштері координата өстерінің таңдап алынған бағытында нөлге тең болады.

Идеал сұйықтар қозғалысының дифференцальды теңдеуін құру үшін тепе-теңдіктегі сұйықтарға арналған Эйлер теңдеуін пайдаланамыз.

Табиғат құбылыстарын зерттегенде, физика жəне техника, химия жəне биология мəселелерін шешкенде, эволюциялық процесті анықтайтын шамалар арасындағы тəуелділік, көбіне, шамалар мен олардың өзгеру жылдамдықтары арасындағы байланыс түрінде, яғни белгісіз функциялар мен туындыларын (дифференциалдарын) байланыстыратын теңдеу ретінде алынады. Белгісіз функция жəне оның туындыларын байланыстыратын мұндай теңдеулер дифференциалдық деп аталады.

Ізделінді функция бір ғана айнымалыдан тəуелді болса, теңдеу кəдімгі дифференциалдық, ал бірнеше айнымалыдан тəуелді болса, дербес туындылы дифференциалдық деп аталады. Мысалы, ең қарапайым кəдімгі дифференциалдық деп, dy / dx = f (x) айтады. f (x) - белгілі, ал y = y(x) - ізделініп отырған белгісіз функция. Бұл теңдеудің шешімдерін f (x) функциясының алғашқы функциялары деп атайтындығы белгілі: Жалпы y = ∫ f(x) dx + C шешімдер жиынтығын береді.

Математикалық ғылым, дифференциалдық теңдеулер теориясы, процестердің математикалық моделдерін құрып, сипаттаушы функционалдық тəуелділіктерін табумен айналысады.

Параллелепипед түрінде қарапайым көлем dx, dy, dz сұйықтықта қозғалады делік (1-суретті қараңыз) . Қысымның және массаның күші, массасы аталған X, Y, Z проекциясы бар қорапта әрекет етеді. Көлем өзгергенде инерция күштері пайда болады. Бұл күштердің координаталық оське, масса бірлігіне бағытталған проекциялары сәйкесінше тең:

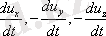
X осіне проекцияланған күштердің тепе-теңдік жағдайын қарастырамы. Сол жақтағы қысым - pdydz, оң жағында

Мұнда,

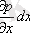
Δp- х осі бойындағы қысымның өзгеруі.

1-сурет.

Сұйықтық көлемінің бірқалыпты қозғалысының схемасы

Массалық күш Xρdxdydz-ке тең. Тепе-теңдік теңдеу былай жазылады:

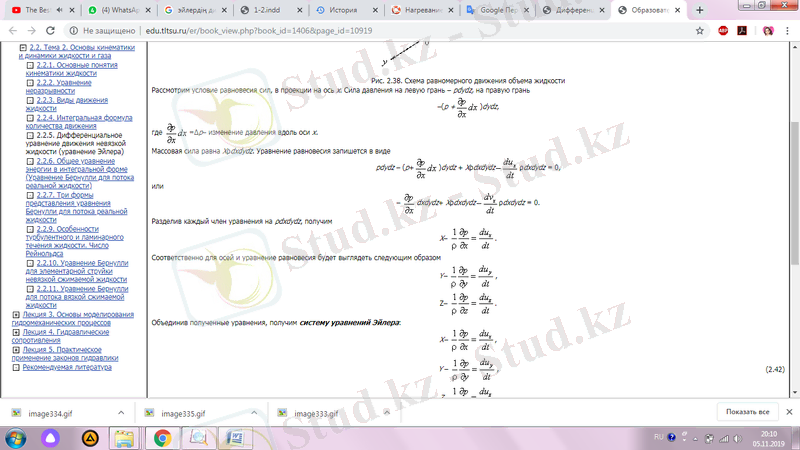
Немесе,

Теңдеудің әрбір шартын ρdxdydz-ке бөліп, аламыз

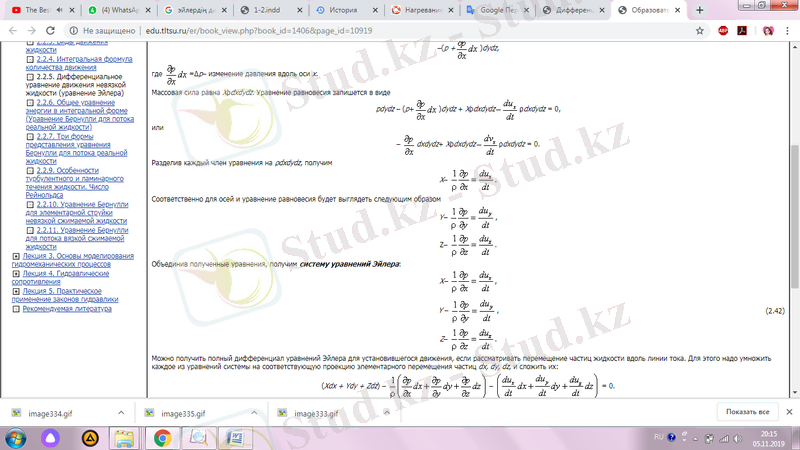
Тиісінше, осьтер мен тепе-теңдік теңдеуі келесідей болады

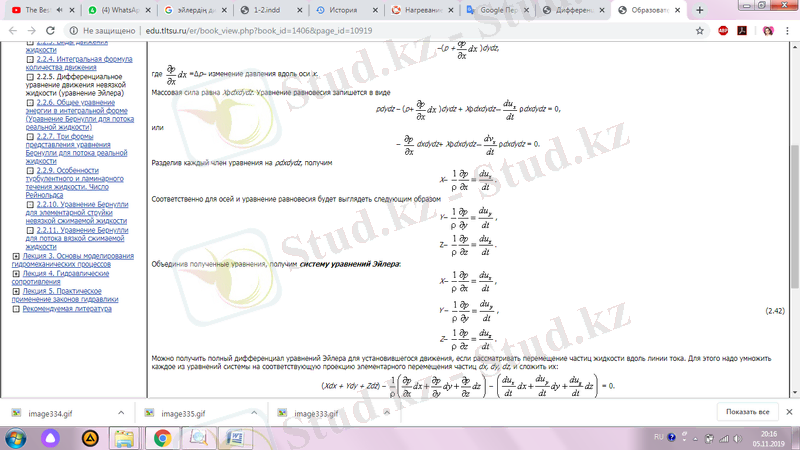
Алынған теңдеулерді біріктіре отырып, Эйлер теңдеулерінің жүйесін аламыз:

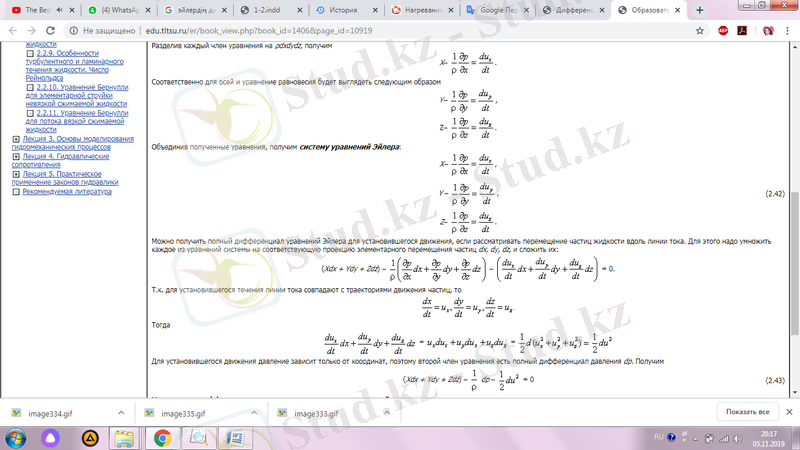
Эйлер теңдеулерін толқындар бойымен сұйықтық бөлшектерінің қозғалысын қарастыра отырып, тұрақты қозғалыс үшін алуға болады. Ол үшін жүйенің әрбір теңдеуін dx, dy, dz бөлшектердің элементар ығысуының тиісті проекциясымен көбейтіп, оларды қосамыз:

Тұрақты ағым үшін ағындар бөлшектердің траекториясына сәйкес келетіндіктен,

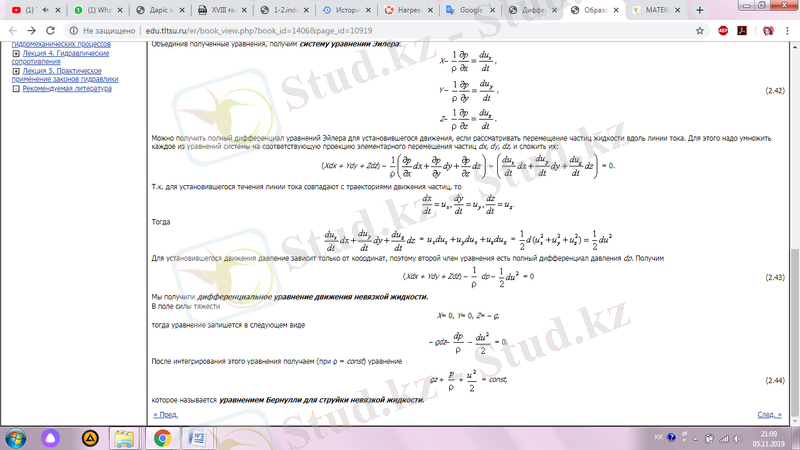
Сонда алатынымыз:

Тұрақты қозғалыс үшін қысым тек координаттарға байланысты болады, сондықтан теңдеудің екінші шарты қысымның толық дифференциалы dp.

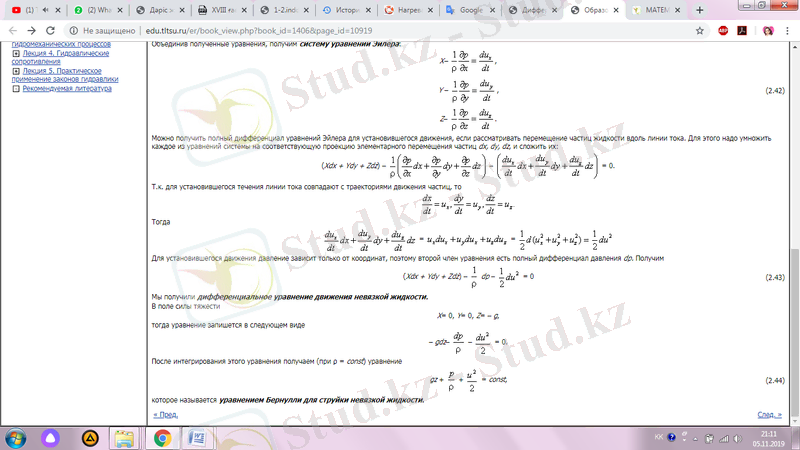
Біз тұтқыр емес сұйықтық қозғалысының дифференциалдық теңдеуін аламыз.

Ауырлық алаңында X= 0, Y= 0, Z= - g,

онда теңдеу келесідей күйде жазылады:

Осы теңдеуді енгізгеннен кейін (ρ= const кезінде) теңдеулерді аламыз:

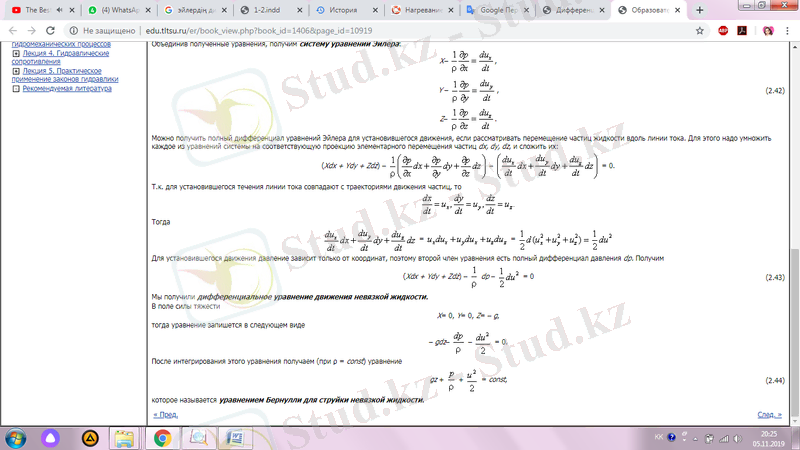
бұл сұйықтық ағынына арналған Бернулли теңдеуі деп аталады.