Сұйық ортадағы қатты бөлшектердің тұнуы: Стокс заңы, Re және Ar критерийлері мен пішін коррекциясы


Баяндама
«Ауырлық күші әсерінен бөлшектердің тұнуы»
Орындаған:
Қабылдаған:
Қарағанды
2018-2019 оқу жылы
Ауырлық күші әсерәнен қатты бөлшектердің қозғалыссыз ортада тұнуын масылға келтіре отырып, сұйықтықта дененің қозғалысын қарастырайық.
Егер m массалы бөлшек ( mg салмағымен) өз салмағының күшімен құлай бастаса, онда оның қозғалыс жылдамдығы бастапқыда уақыт өте келе ұлғаяды. Орта қарсылығының толық болмауынан w жылдамдық бәрімізге белгілі w=gr заңымен уақытқа байланысты өзгеретін еді. Бірақ та, жылдамдық ұлғайған сайын бөлшектің қозғалысқа қарсылығы күшееді, 1-теңдеуде берілгендей, сәйкесінше оның жылдамдануы азаяды.
Соңында, қысқа уақыт өткеннен кейін динамикалық тепе-теңдік орнайды: бөлшекті қозғалтатын ауырлық күші ортаның қарсылық күшіне теңеседі. Осы сәттен бастап, қозғалыс жылдамдауы нөлге тең болады және бөлшек тұрақты жылдамдықпен біркелкі қозғала бастайды. Осындай ортадағы біркелкі қозғалыстың жылдамдығы тұну жылдамдығы деп аталады және w 0 белгісімен көрсетіледі.
d диаметрлі шар тәрізді бөлшекті қозғайтын күш оның салмағы мен итеретін бөлшек көлемінде сұйықтық (орта) салмағына тең архимед күшімен анықталады:
мұнда, p т - қатты бөлшектің тығыздығы; р - орта тығыздығы
1-теңдеуге сәйкес орта қарсылығының күші:
w 0 тұну жылдамдығын бөлшекті қозғалысқа келтіретін күш теңдігі шарты мен орта қарсыластығынан табуға болады:
Қарсылық коэффициенті мәні тәуелділіктің бір түрімен анықтауға болады - 1. 1, 1. 2 немесе 1. 3.
- мәнін 4-теңдеуге алмастырып қойғанда ламинарлы аймақ үшін болады:
Мұнда, µ - орта тұтқырлығы.
Бұл теңдеуді Стокс заңы мәнін қолданған кезде де пайдалануға болады. Стокс заңынан сәйкес ұсақ бөлшектердің тұнуы кезіндегі орта қарсыластығы мына тәуелділікпен анықталады:
Қозғалыстағы күшті орта қарсыластығы күшіне теңестіреміз:
Осыдан w oc -ны осы теңдеуден анықтап, 5-теңдеуді шығарамыз.
Стокс заңына қатысты жүретін тұну кезінде ұсақ бөлшектердің максимальды көлемін 5-теңдеуде тұну жылдамдығы орынына Рейнольдс критерийі және Re=2 қабылдау арқылы айқындау арқылы табуға болады.
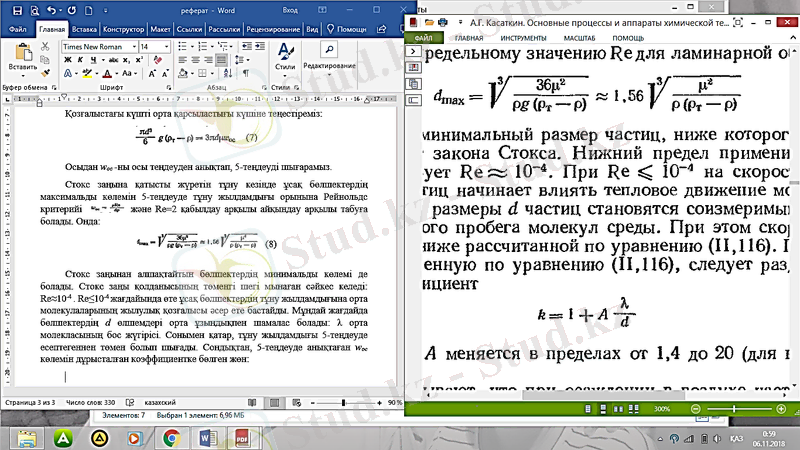 Стокс заңынан алшақтайтын бөлшектердің минимальды көлемі де болады. Стокс заңы қолданысының төменгі шегі мынаған сәйкес келеді: Re≈10
-4
. Re≤10
-4
жағдайында өте ұсақ бөлшектердің тұну жылдамдығына орта молекулаларының жылулық қозғалысы әсер ете бастайды. Мұндай жағдайда бөлшектердің
d
өлшемдері орта ұзындықпен шамалас болады: λ орта молекласының бос жүгірісі. Сонымен қатар, тұну жылдамдығы 5-теңдеуде есептегеннен төмен болып шығады. Сондықтан, 5-теңдеуде анықтаған
w
oc
өлшемін дұрысталған коэффициентке бөлген жөн:
Стокс заңынан алшақтайтын бөлшектердің минимальды көлемі де болады. Стокс заңы қолданысының төменгі шегі мынаған сәйкес келеді: Re≈10
-4
. Re≤10
-4
жағдайында өте ұсақ бөлшектердің тұну жылдамдығына орта молекулаларының жылулық қозғалысы әсер ете бастайды. Мұндай жағдайда бөлшектердің
d
өлшемдері орта ұзындықпен шамалас болады: λ орта молекласының бос жүгірісі. Сонымен қатар, тұну жылдамдығы 5-теңдеуде есептегеннен төмен болып шығады. Сондықтан, 5-теңдеуде анықтаған
w
oc
өлшемін дұрысталған коэффициентке бөлген жөн:
(9)
А өлшемі 1, 4-тен 20-ға дейін өзгеріп тұрады (ауа үшін A=1. 5) .
Есептеулер бойынша, ауада d>3 мкм өлшемді шаң бөлшектерінің тұнуы кезінде коэффициент k≈1. d≈0. 1 мкм кезінде шаң тұнбайды, тек олардың бөлшектерінің хаотикалық броундық қозғалысы байқалады.
 2<Re<500 ауыспалы аймағы жағдайында 1. 1 мәнін 4-теңдеуге алмастырғаннан кейін болады:
2<Re<500 ауыспалы аймағы жағдайында 1. 1 мәнін 4-теңдеуге алмастырғаннан кейін болады:
(10)
 Сәйкесінше, автомодельді аймақ үшін (Re>500) 1. 3 теңдеуіне сай қарсылық коэффициентін 0, 44-ке теңестіріп, 4-теңдеуде орнын ауыстырсақ, болады:
Сәйкесінше, автомодельді аймақ үшін (Re>500) 1. 3 теңдеуіне сай қарсылық коэффициентін 0, 44-ке теңестіріп, 4-теңдеуде орнын ауыстырсақ, болады:
(11)
Тұнудың осы аймағына сәйкес есептеулік теңдеуді таңдау үшін, яғни 5, 10, 11-теңдеулердің біреуін, Rе критерийлерінің өлшемдерін алдын-ала білу керек. Бұл критерий ішіне w oc іздеп отырған тұну жылдамдығы кіреді. Сондықтан, жоғарыда көрсетілгендей w oc есептеуі бірізді жақындастыру әдістерімен ғана жүзеге асады. Тұну белгілі бір аймақта болатынын ескерсек, мысалы, ламинарлы, w oc -ты сәйкесінше теңдеу арқылы анықтайды және осы өлшеммен Re-ні есептейді. Кейін анықталған Re мәні тұну аймағына жауапты шекарада тұрғандығын тексереді. Сәйкес келмеген жағдайда есептеулерді сәйкес қорытындыға келгенге дейін қайталап жүргізеді.
Бірізді жақындастыру әдісінің қиындығы салдарынан w oc -ты анықтауға Лященко П. В. ұсынған басқа әдіспен қолданған ыңғайлы. Бұл әдіс 4-теңдеуді түрлендірге негізделген: Re арқылы көрсетілген тұну жылдамдығының орнын ауыстыру және теңдеудің екі бөлігін де екі еселенуі.
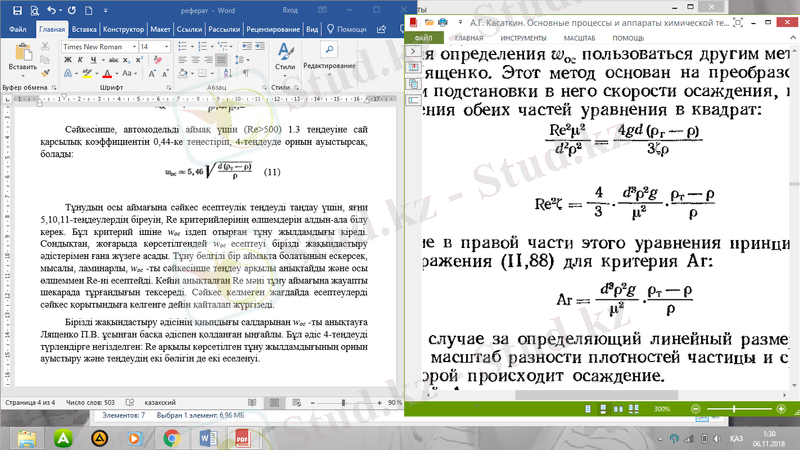
осыдан
(12)
Бұл теңдеудің оң жақ бөлігіндегі мәндері 13-теңдеу мәндерінен аса қатты ерекшеленбейді, Ar критерийі үшін:

(13)
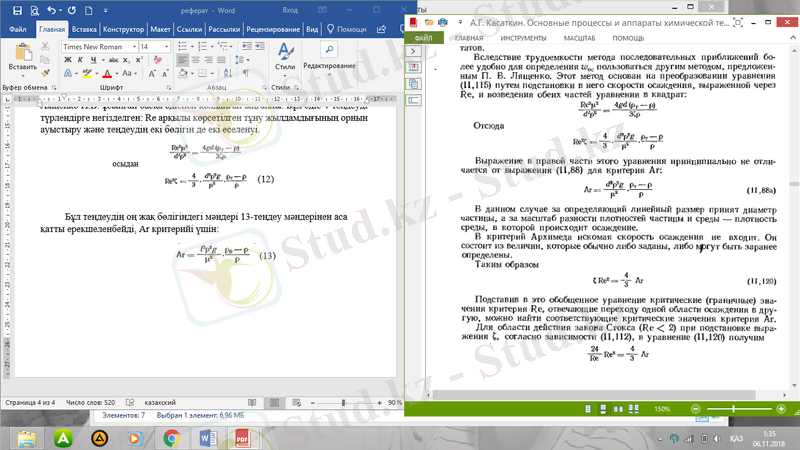
(13а)
Берілген жағдайда анықтаушы сызықты өлшем үшін бөлшек диаметрі, ал орта және бөлшек тығыздығы әр түрлігінің масштабына - тұну жүріп жатқан орта тығыздығы алынған.
Осы жалпыланған теңдеуге критикалық Re мәнін қоятын болсақ, сәйкес критикалық Ar мәнін табуға болады.
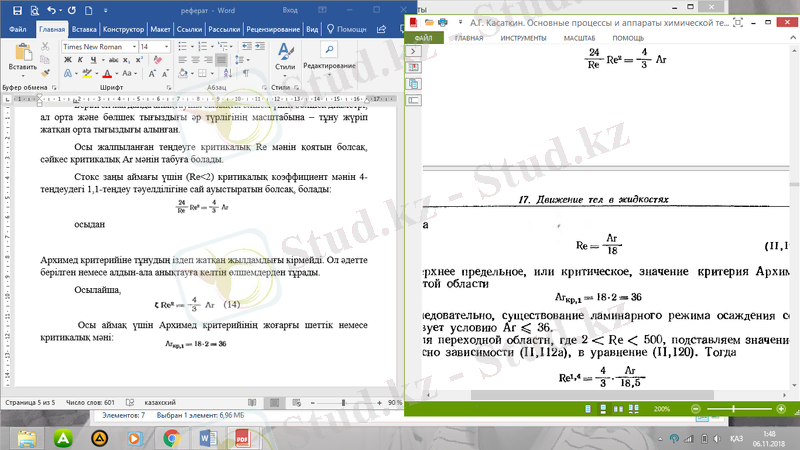
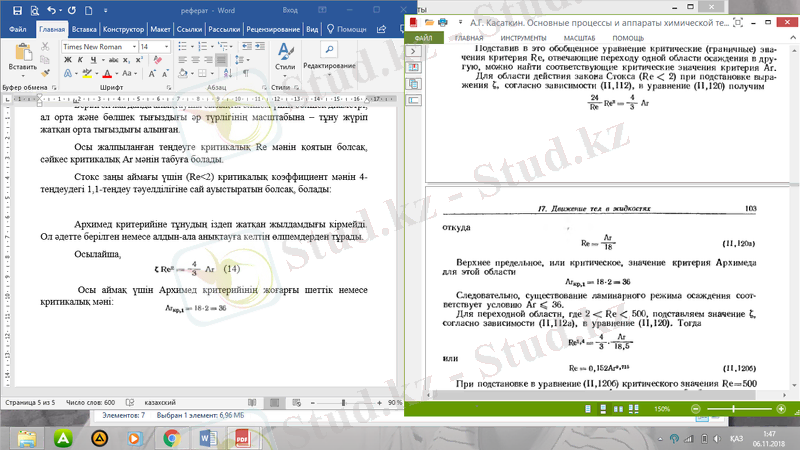 Стокс заңы аймағы үшін (Re<2) критикалық коэффициент мәнін 4-теңдеудегі 1, 1-теңдеу тәуелділігіне сай ауыстыратын болсақ, болады:
Стокс заңы аймағы үшін (Re<2) критикалық коэффициент мәнін 4-теңдеудегі 1, 1-теңдеу тәуелділігіне сай ауыстыратын болсақ, болады:
 осыдан
осыдан
(14)
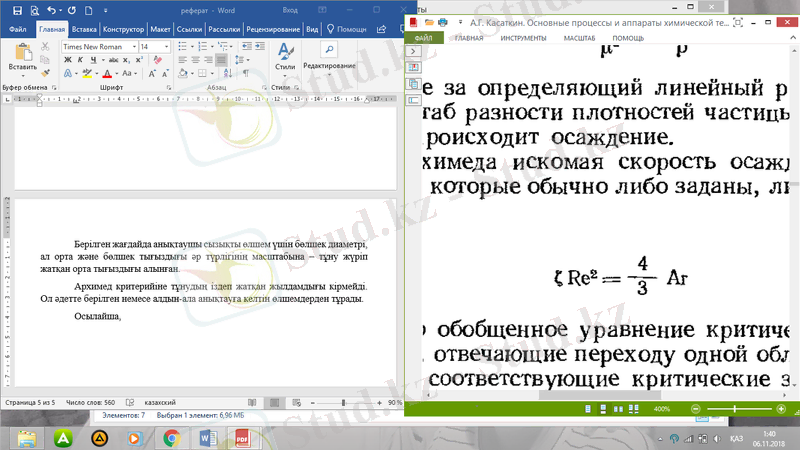
Архимед критерийіне тұнудың іздеп жатқан жылдамдығы кірмейді. Ол әдетте берілген немесе алдын-ала анықтауға келтін өлшемдерден тұрады.
 Осылайша,
Осылайша,
(15)
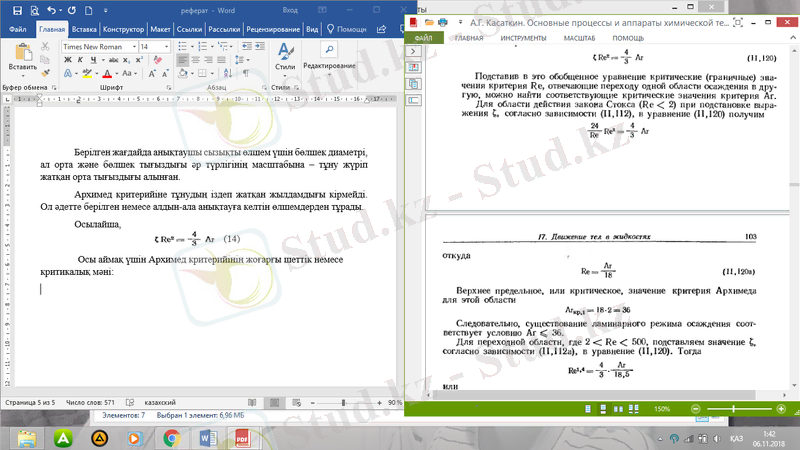 Осы аймақ үшін Архимед критерийінің жоғарғы шеттік немесе критикалық мәні:
Осы аймақ үшін Архимед критерийінің жоғарғы шеттік немесе критикалық мәні:
(16)
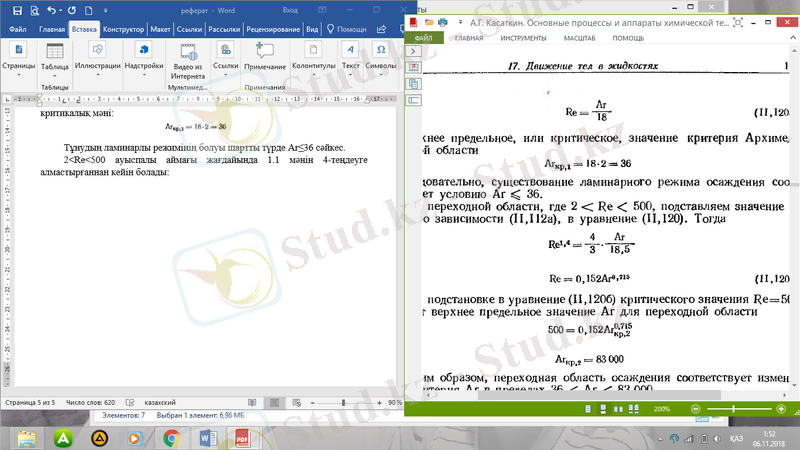 Тұнудың ламинарлы режимінің болуы шартты түрде Ar≤36 сәйкес. 2<Re<500 ауыспалы аймағы жағдайында 1. 1 мәнін 4-теңдеуге алмастырғаннан кейін болады:
Тұнудың ламинарлы режимінің болуы шартты түрде Ar≤36 сәйкес. 2<Re<500 ауыспалы аймағы жағдайында 1. 1 мәнін 4-теңдеуге алмастырғаннан кейін болады:
(17)
немесе
17 теңдеуіне Re=500 мәнін қойғанда, ауыспалы аймақтағы Ar үшін жоғарғы шекаралық мәнін табады.
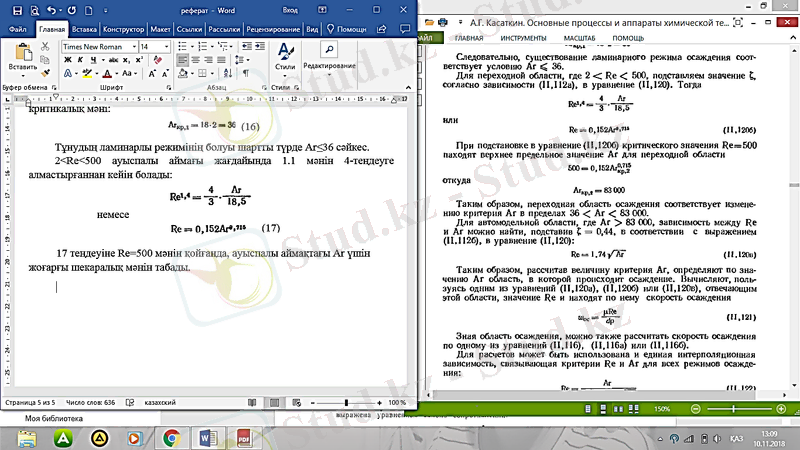
(18)
осыдан
Осылайша, тұнудың ауыспалы аймағы Ar критерийінің өзгерісіне 36< Ar < 83000 тең.
Ar>83000 - ға тең автомодельді аймақ үшін 17-теңдеуді 15-теңдеудегі l=0, -ті қойып, Re және Ar арасындағы тәуелділікті анықтаймыз.

(19)
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz