Тұрақты ток тізбегінің электрлік күйін талдауға арналған әдістемелік нұсқау: Кирхгоф заңдары, контурлық токтар және эквивалентті генератор әдістері


КІРІСПЕ
Тұрақты ток тізбегінің электрлік күйін талдауға арналған әдістемелік нұсқау.
1. Тапсырма және орындауға қойылатын жалпы талаптар
Тапсырманың мазмұны.
- Сұлбаның барлық тармақтарындағы токтарды есептеу үшін Кирхгоф заңдары бойынша теңдеулер жүйесін құрыңдар.
- Берілген электр тізбегінің тармақтарындағы барлық токтарды контурлық токтар әдісімен анықтаңдар.
- Есептелген сұлба үшін қуаттар балансын құрыңдар.
- Сыртқы контур үшін масштаб бойынша потенциалдық диаграмма тұрғызыңдар.
- Эквивалентті генератор әдісін пайдаланып, тек қана бір тармақтан өтетін токтың сандық мәнін анықтаңдар.
Тапсырманы орындауға қойылатын жалпы талаптар. Тапсырманы орындау алдында “Тұрақты токтың сызықтық электр тізбегі“ тарауынан келесі сұрақтарды қайталау қажет:
- Тұрақты ток электр тізбегін сипаттайтын негізгі параметрлері.
- Тұрақты ток тізбегі үшін Ом, Кирхгоф заңдары.
- Электр тізбектернің есептеу әдістері (контурлық токтар әдісі, эквивалентті генератор әдісі, электр тізбегіндегі пассивті элементтерді түрлендіру әдісі) .
Қайталаған кезде “Тұрақты токтың сызықты электр тізбегі“ тарауы бойынша лекция материалдарын және [1, 2, 3, 4, 5] әдебиеттерді пайдаланыңыздар.
- ӘДІСТЕМЕЛІК НҰСҚАУЛАР
Сызықты электр тізбектерінің негізгі қасиеттері және жалпылай талдау әдістері.
Электр тізбектерінің негізгі заңдары. Электр тібектерін есептеуге жататын, негізгі заңдар - Ом және Кирхгоф заңдары. Ом заңы ток пен кернеу арасында байланыс орнатады, және электр тізбегінің бөлігі үшін төмендегідей жазылу мүмкін:
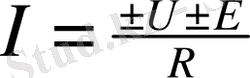
мұнда U мен E “+” оң таңбамен алынады, егер олардың бағытары тоқтың бағытымен сәйкес келсе, ал олардың бағыттары токтың бағытына қарама - қарсы болса U мен E “-” теріс таңбамен алынады: R - тізбек бөлігіндегі кедергілер қосындысы.
Кирхгоф заңдары келесі түрде баяндалады және жазылады.
Кирхгофтың бірінші заңы. Бір түйінде қосылатын, тармақтардағы токтардың алгебралық қосындысы нөлге тең болады, яғни
;
мұнда m - қарастырылып отырған түйінде қосылған тармақтардың саны.
Кирхгофтың екінші заңы. Кез келген контурдағы кернеулердің алгебралық қосындысы осы контурдағы э. қ. к. -ң алгебралық қосындысына тең болады, яғни
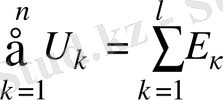 ;
;
n - контурдағы кернеулер саны,
 - контурдағы э. қ. к. саны.
- контурдағы э. қ. к. саны.
Бастапқы берілгендер саны жеткілікті болған кезде, R және E бар күрделі электр тізбектер саны қанша болса да, оларды есептеуге болады. Теңдеулер жүйесін құрған кезде, егер қарастыратын электр тізбегінде “m” тармақтар және “n” түйіндер бар болса, онда Кирхгофтың бірінші заңы негізінде құрылатын теңдеулер саны n -1, ал Кирхгофтың екінші заңы негізінде [m - (n - 1) ] болатынын ескеру керек.
Сонымен, Кирхгофтың бірінші және екінші заңдары бойынша құрылған жалпы теңдеулер саны, электр тізбегіндегі тармақтар санына тең болады.
Күрделі электр тізбегін есептегенде, жүйеге кіретін теңдеулер саны өте көп болса мұндай жүйені шешуге көп уақыт кетеді. Күрделі электр тізбегін есептеуді жеңілдетуге мүмкіндік туғызатын, әдіс - ол контурлық токтар әдісі. Эквивалеттік генератор әдісі бөлек жеке алынған тармақтағы токты анықтауға мүмкіндік туғызады.
Кирхгоф заңдарын, контурлық токтар әдісін және эквиваленттік генератор әдісін қолдануды нақты мысал арқылы көрсетеміз.
- БАҚЫЛАУ МЫСАЛЫБастапқы берілгендеріБерілгені: E1= 24 B ; E2= 42 B ;
R 10 = R 20 = 1 Oм ; R 1 = 11 Oм ;
R 2 = 17 Oм ; R 3 = R 4 = 12 Oм ;
R 5 = R 6 = 6 Oм.
- Табу керек: 3. 1 суретте көрсетілген, сұлба тармақтарындағы токтарды, Кирхгоф заңдары бойынша анықтаңдар.
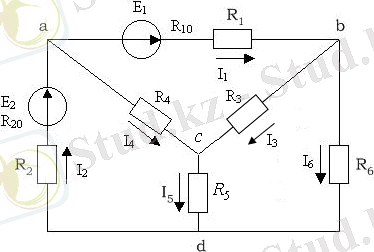
3. 1сурет
Шешуі:
Берілген тізбекте 6 тармақ және 4 түйін бар. Өз қалауымыз бойынша тармақтардағы токтардың бағыттарын көрсетеміз. Кирхгофтың бірінші заңы бойынша 3 теңдеу құрамыз (n-1=4 -1=3)
“a” түйіні үшін
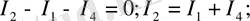
“b” түйіні үшін
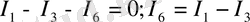 (1)
(1)
“с” түйіні үшін
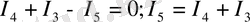
Кирхгофтың екінші заңы бойынша теңдеу құру үшін сұлбаны үш аbса, асdа, сbdс контурға бөлеміз. Контурларды айналып өту бағытын сағат тілі бойынша аламыз. Теңдеулер саны:
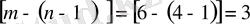
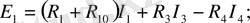
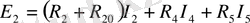 (2)
(2)
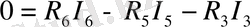
Егер (1) теңдеулердегі I
2
, I
5
, I
6
токтардың мәнін (2) жүйеге қойса, онда үш белгісіз бар үш теңдеулер жүйесін табамыз
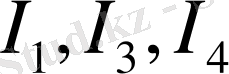 :
:
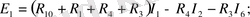
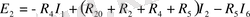
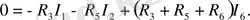
Э. Қ. К. -ң және кедергілердің сан мәндерін қойғаннан кейін:
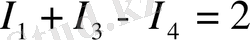
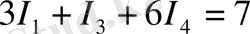 (3)
(3)
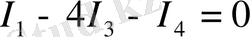
(3) -ті кез келген тәсілмен шешіп, токтарды табамыз:
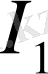 =
=
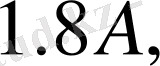


- теңдеулер жүйесінен қалған токтарды табамыз:
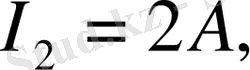

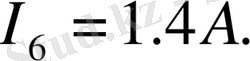
3. 2 суреттегі сұлбаның тармақтарындағы токтарды контурлық токтар әдісімен анықтау. Контурлық токтар әдісі электр тізбегінде қажетті тәуелсіз контурлар санын таңдаудан басталады. Тәуелсіз контурлар саны мына өрнекпен [m-n+1] анықталады (мұнда m- тармақтар саны, n- түйіндер саны) . Әрбір таңдалған контурлардағы контурлық токтардың бағыттарын өз қалауымызша аламыз.
Кирхгофтың екінші заңы бойынша теңдеулер жүйесі құрылады. Алынған теңдеулер жүйесін шешіп, контурлық токтарды және сол арқылы тармақтардағы токтарды анықтаймыз.
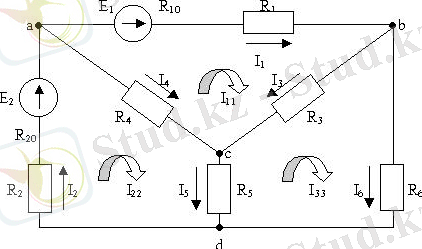
3. 2 сурет
Үш контурлық токтарды I 11 ; I 22 ; I 33 деп белгілейміз. Үш контур үшін Кирхгофтың екінші заңы бойынша теңдеулер құрамыз:
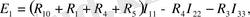
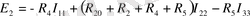 (4)
(4)
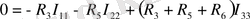
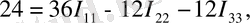
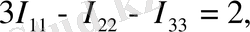
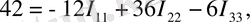
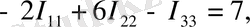
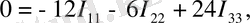
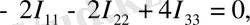
(4) теңдеулер жүйесін шешіп, контурлық токтарды анықтаймыз. Егер контурлық токтың таңбасы «-» болып шықса, онда шын контурлық токтың бағыты сұлбада алынған бағытқа қарама-қарсы екенін білдіреді.
Біздің жағдайда:
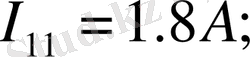
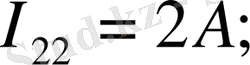
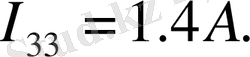
Енді тармақтардағы токтарды анықтаймыз:
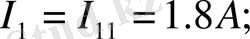

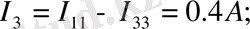
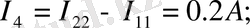
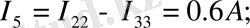
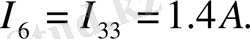
Алынған мәліметтер бойынша сұлбадағы токтардың шын бағытын көрсетеміз.
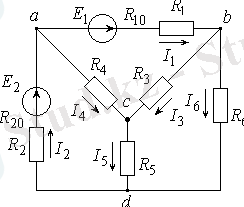
3. 3 сурет.
3. 1. 4. Қуаттар балансын тексеру
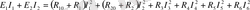 . 3
. 3
127. 2 Вт = 127. 2 Вт.
Ескерту
Егер Е. Қ. К. мен токтың бағыттары бірдей болса, онда
 көбейтіндісі «+» оң таңбамен алынады, егер бірдей болмаса, онда көбейтіндісі «-» теріс таңбамен алынады.
көбейтіндісі «+» оң таңбамен алынады, егер бірдей болмаса, онда көбейтіндісі «-» теріс таңбамен алынады.
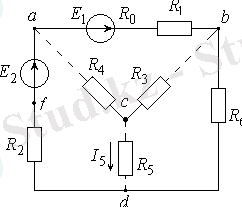
- Сыртқы контур үшін потенциалдық диаграмма құру.
Біздің сұлбаның сыртқы контуры dfakbd болады. «d» нүктенің потенциалын
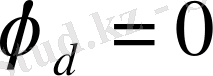 деп аламыз. “d” түйіннен бастап, сыртқы контурды сағат тілі бойынша жүріп өтеміз және сұлбаның жеке бөліктерінің потенциалдарын табамыз:
деп аламыз. “d” түйіннен бастап, сыртқы контурды сағат тілі бойынша жүріп өтеміз және сұлбаның жеке бөліктерінің потенциалдарын табамыз:
 f
=
f
=
 d
d
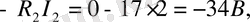
a =
+
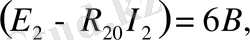
k =
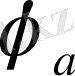
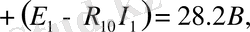
 b
=
b
=
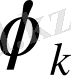 k
k
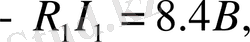
 d
=
d
=
 b
b
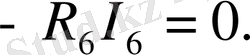
Потенциалдар мен кедергілер үшін масштап таңдап аламыз
 =
=
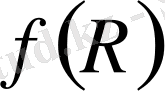 тәуелділік графигін тұрғызамыз.
тәуелділік графигін тұрғызамыз.
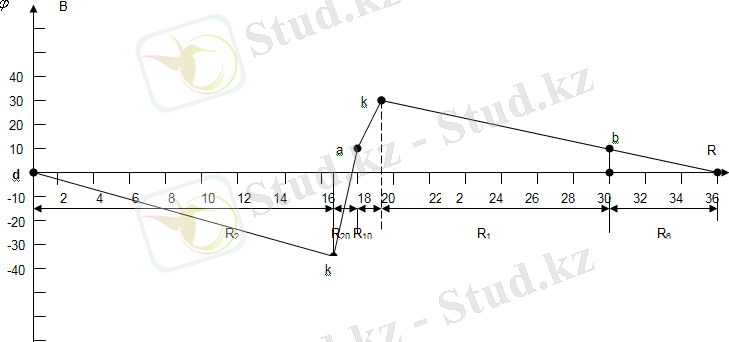
3. 4 сурет.
3. 1. 6 Эквиваленттік генератор әдісімен “ав” тармағындағы (I ав ) токты анықтау.
Эквиваленттік генератор әдісі, күрделі электр тізбегінің тек бір ғана тармағындағы токты анықтау қажет болғанда қолданылады. Бұл әдіс бойынша күрделі тізбектегі барлық эқк-ң зерттелетін тармаққа тигізетін әсерін осы тармаққа тізбектеп қосылған эквивалентті қорек көзімен (генератормен) алмастыруға болады. Бұл қорек көзінің эқк-і тізбектен ажыратылған, зерттелетін тармақтың қысқаштарындағы бос жүріс кернеуіне тең және оның ішкі кедергісі R Э =R кір зерттелетін тармақтың қысқаштарына қатысты пассивті екі ұштының кірмелік кедергісіне тең болады.
Есептеу келесідей болады:
1) Тармақтағы токтың оң бағытын таңдап алады (біздің жағдайда “a” - дан “b” - ға ) және токты төмендегі формула бойынша анықтайды :
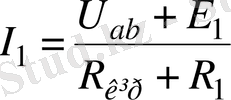
мұнда
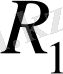 - зерттелетін тармақтың кедергісі,
- зерттелетін тармақтың кедергісі,
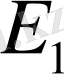 - зерттелетін тармақтың э. қ. к. Егер зерттелетін тармақта э. қ. к. жоқ болса, онда ол нөлге тең деп алынады. “+” немесе “-“ таңбалары қорек көзі бар тармақ үшін арналған Ом заңына сәйкес таңдап алынады, яғни егер э. қ. к. бағыты токтың бағытымен бірдей болса, онда ”оң ” таңба алынады, кері жағдайда “теріс” таңба алынады.
- зерттелетін тармақтың э. қ. к. Егер зерттелетін тармақта э. қ. к. жоқ болса, онда ол нөлге тең деп алынады. “+” немесе “-“ таңбалары қорек көзі бар тармақ үшін арналған Ом заңына сәйкес таңдап алынады, яғни егер э. қ. к. бағыты токтың бағытымен бірдей болса, онда ”оң ” таңба алынады, кері жағдайда “теріс” таңба алынады.
2) Тогын анықтауға тиіс тармақты ажыратады, және кез келген әдістердің бірімен ажыратылған тармақтың ұштарындағы U авбж кернеуін анықтайды.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz