Сызықтық емес программалаудың классикалық әдістері: экстремумдар мен бірінші ретті туынды арқылы зерттеу


Сызықтық емес программалаудың классикалық әдістері.
Теорема 1.
(Экстремумның бар болуының қажеттілік шарты) . Егер дифференциалданатын
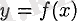 функцияның
функцияның
 нүктесінде максимум немесе минимум мәні бар болатын болса, онда бұл нүктеде оның туындысы нольге айналады, яғни
нүктесінде максимум немесе минимум мәні бар болатын болса, онда бұл нүктеде оның туындысы нольге айналады, яғни
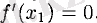 .
.
Туындысы нольге айналатын немесе үзіліс нүктесі болатын аргумент мәндері сыни (күдікті) нүктелер немесе сыни (күдікті) мәндер деп аталады.
Функцияның экстремумдарын табу үшін барлық сыни (күдікті) нүктелерді табады, одан кейін әрбір сыни (күдікті) нүктені жеке зерттей отырып, бұл нүктеде максимум немесе минимум бар ма, әлде максимум да, минимум да жоқ па соны анықтайды.
Сыни нүктелердегі функцияны зерттеуде келесі теоремаға сүйенеміз.
Теорема 2. (Экстремумның бар болуының жеткілікті шарты) .
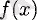 функциясы
функциясы
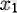 сыни (күдікті) нүктесі жататын қандай да бір интервалда үздіксіз функция, және осы интервалдың барлық нүктелерінде дифференциалданатын болсын. Егер осы нүкте арқылы солдан оңға өткенде туынды таңбасы плюстен минуске өзгерсе, онда
сыни (күдікті) нүктесі жататын қандай да бір интервалда үздіксіз функция, және осы интервалдың барлық нүктелерінде дифференциалданатын болсын. Егер осы нүкте арқылы солдан оңға өткенде туынды таңбасы плюстен минуске өзгерсе, онда
 үшін функцияның максимумы бар болады. Егер
үшін функцияның максимумы бар болады. Егер
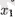 нүктесі арқылы солдан оңға өткенде туынды таңбасы минустен плюске өзгерсе, онда
нүктесі арқылы солдан оңға өткенде туынды таңбасы минустен плюске өзгерсе, онда
 нүктесінде функцияның минимумы бар болады.
нүктесінде функцияның минимумы бар болады.
Сонымен,
егер а)
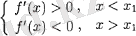 болса, онда
болса, онда
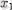 нүктесінде функцияның максимумы болады;
нүктесінде функцияның максимумы болады;
ал егер б)
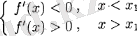 болса, онда
болса, онда
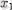 нүктесінде функцияның минимумы болады.
нүктесінде функцияның минимумы болады.
1-сурет теорема2-ның мағынасын көрнекі бейнелейді.

Сурет 1
 нүктесінде
нүктесінде
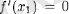 бар болсын және
бар болсын және
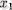 нүктесіне жақын барлық
нүктесіне жақын барлық
 үшін төмендегі теңсіздіктер орындалсын
үшін төмендегі теңсіздіктер орындалсын
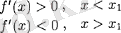
Сонда
 үшін, қисыққа жүргізілген жанама
үшін, қисыққа жүргізілген жанама
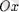 осімен сүйір бұрыш жасайды - функция өседі, ал
осімен сүйір бұрыш жасайды - функция өседі, ал
 үшін, қисыққа жүргізілген жанама
үшін, қисыққа жүргізілген жанама
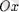 осімен тұйық бұрыш құрайды - функция кемиді;
осімен тұйық бұрыш құрайды - функция кемиді;
 үшін функция өсуден кемуге ауысады, яғни максимумы бар.
үшін функция өсуден кемуге ауысады, яғни максимумы бар.
Егер
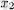 нүктесінде
нүктесінде
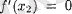 болса және
болса және
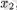 нүктесіне жақын барлық
нүктесіне жақын барлық
 үшін төмендегі теңсіздіктер орындалса
үшін төмендегі теңсіздіктер орындалса
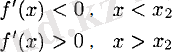
онда
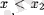 үшін, қисыққа жүргізілген жанама
үшін, қисыққа жүргізілген жанама
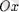 осімен тұйық бұрыш жасайды - функция кемиді, ал
осімен тұйық бұрыш жасайды - функция кемиді, ал
 үшін, қисыққа жүргізілген жанама
үшін, қисыққа жүргізілген жанама
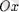 осімен сүйір бұрыш құрайды - функция өседі;
осімен сүйір бұрыш құрайды - функция өседі;
 үшін функция кемуден өсуге ауысады, яғни минимумы бар.
үшін функция кемуден өсуге ауысады, яғни минимумы бар.
Егер
 нүктесінде
нүктесінде
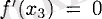 болса және
болса және
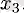 нүктесіне жақын барлық
нүктесіне жақын барлық
 үшін төмендегі теңсіздіктер орындалса
үшін төмендегі теңсіздіктер орындалса
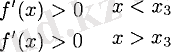
онда
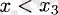 үшін де,
үшін де,
 үшін де функция өседі. Сондықтан
үшін де функция өседі. Сондықтан
 үшін функцияның максимумы да, минимумы да болмайды.
үшін функцияның максимумы да, минимумы да болмайды.
Бірінші ретті туынды көмегімен дифференциалданатын
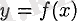 функцияны максимум және минимумға зерттеу схемасы:
функцияны максимум және минимумға зерттеу схемасы:
- Функцияның бірінші ретті туындысын, яғнитабамыз
- аргументінің сыни (күдікті) мәндерін табамыз; ол үшін:
а) бірінші туындыны нольге теңестіреміз және алынған
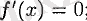 теңдеудің нақты түбірлерін табамыз;
теңдеудің нақты түбірлерін табамыз;
б)
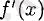 туындысында үзіліс нүктесі болатын
туындысында үзіліс нүктесі болатын
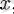 -тің мәндерін табамыз
-тің мәндерін табамыз
- Сыни (күдікті) нүктенің оң және сол жақтарында туындының таңбасын зерттейміз. Туынды белгісі екі сыни (күдікті) нүктенің арасындағы аралықта өзгеріссіз болғандықтан (сурет 1), мысалы, сыни (күдікті) нүктесінің сол және оң жақтағы туынды таңбасын зерттеу үшін, жәненүктелеріндегі туындының таңбасын анықтау жеткілікті
(
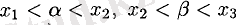 , мұндағы
, мұндағы
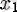 және
және
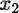
жақын сыни (күдікті) нүктелер) .
Аргументтің әрбір критикалық мәні үшін
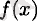 функциясының мәнін есептейміз.
функциясының мәнін есептейміз.
Осылайша, мүмкін болатын жағдайлардың төмендегідей схемалық кескінін аламыз
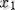 критикалық нүктесінен өту кезіндегі
критикалық нүктесінен өту кезіндегі
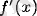 туындысының таңбалары
туындысының таңбалары
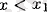
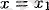

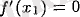
немесе үзіледі
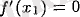
немесе үзіледі
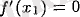
немесе үзіледі
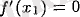
немесе үзіледі
Мысал 1. Төмендегі функцияны максимум және минимумға зерттеңдер:
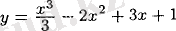
Шешуі:
- Бірінші ретті туындысын табамыз

- Туындының нақты түбірлерін табамыз, яғни стационар (күдікті, сыни) нүктелерді табамыз
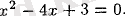

Туынды барлық жерде үздіксіз. Яғни басқа сыни (күдікті) нүктелер жоқ.
- Сыни (күдікті) мәндерді зерттейміз, және зерттеу нәтижесін 2-суретке саламыз
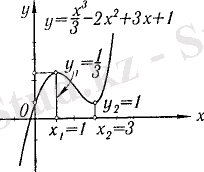
Сурет 2
Бірінші
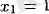 сыни (күдікті) нүктені зерттейміз.
сыни (күдікті) нүктені зерттейміз.
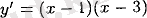 болғандықтан
болғандықтан
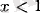 үшін
үшін
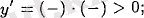
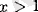 үшін
үшін
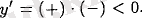
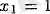 мәні арқылы сол жақтан оң жаққа өткенде туындының таңбасы плюстен минуске ауысады. Яғни,
мәні арқылы сол жақтан оң жаққа өткенде туындының таңбасы плюстен минуске ауысады. Яғни,
 үшін функцияның максимумы болады, атап айтқанда
үшін функцияның максимумы болады, атап айтқанда
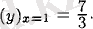
Екінші
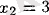 сыни (күдікті) нүктені зерттейміз.
сыни (күдікті) нүктені зерттейміз.
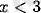 үшін
үшін
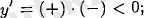
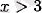 үшін
үшін
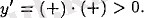
Яғни,
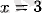 мәні арқылы сол жақтан оң жаққа өткенде туындының таңбасы минустен плюске ауысады. Яғни,
мәні арқылы сол жақтан оң жаққа өткенде туындының таңбасы минустен плюске ауысады. Яғни,
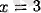 үшін функцияның минимумы болады, атап айтқанда
үшін функцияның минимумы болады, атап айтқанда
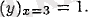
Жүргізілген зерттеу нәтижесін 2-суретке саламыз.
Сызықтық емес программалаудың классикалық әдістері тақырыбына арналған тапсырмалар
Төмендегі функциялардың экстремумдарын табыңыздар
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz