Көпбұрыштар ауданын оқытудың теориялық негіздері

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 61 бет
Таңдаулыға:

арнасы ол емес. Геометрияда қолданылатын мәселелер сан алуан. Сондықтан геометрия ерте заманның өзінде-ақ кеңістіктік пішіндер мен қатынастар жөніндегі ғылым ретінде қалыптасқан. Жер өлшеу ғылымын, соңғы мағынадағы геометриядан айырып айту үшін, Аристотель геодезия деп атаған. Геометрияны тек жер өлшеу жұмыстары ғана тудырған жоқ. Бұл бағытта ғылыми-практикалық деректердің молайып, қорлануына үй, көпір, пирамида, әскери бекіністер, т. б. құрылыстар салу, арналар қазу, ыдыстардың сыйымдылығын өлшеу, құрылыстарға қажетті материалдардың шамасын алдын ала есептеу елеулі әсер етті. Геометрия ұғымдары дүниеде кездесетін заттардың дербес физикалық қасиеттерін еске алмай, абстракциялап (яғни, дерексіздендіріп), олардың тек мөлшері мен өзара орналасуын ғана қарастыру нәтижесінде пайда болған. Қалыпқа салынып соғылған кірпіштердің, құрылысқа арналып шабылған қырлы тастардың, шеберлердің кесіп, сүргілеп тегістеген бұйымдарының сыртқы тұрпаты - пішіні бірдей болады. Мұндай пішін төрт бұрышты призма деп аталады. Үш бұрышты, бес бұрышты, т. б. призмалар болады. Геометрияда призманың қандай материалдан жасалғандығы есепке алынбайды, оның тек мөлшері мен орналасуы ғана зерттеледі. Цилиндр, конус, шар, т. б. ұғымдар да осылай қалыптасқан. Сонымен геометриялық денелер - температурасы, массасы, жасалған материалы мен жеке қасиеттері қарастырылмайтын физикалық денелер. [28] -[40] .

Жіңішке жіп, бір тал қыл, сәуле, сым, т. б. негізінде шектеусіз жіңішке сызық ұғымы шыққан. Геометриялық денелерді ойша топшылап, шектеусіз кішірейте беруге болады. Осыдан нүкте ұғымы шығады. Нүкте дененің әбден кішірейіп, тоқтаған шектік жағдайы деп есептеледі. Геометрия тұрғысынан алғанда нүктені одан әрі кішірейтуге болмайды. Геометриялық денелердің, беттердің, сызықтардың және нүктелердің кез келген жиыны фигура деп аталады. Геометрия алғашқы кезде фигуралардың мөлшерлерін, өзара орналасу тәртібін, бір түрден екінші түрге көшу жолдарын зерттейтін ғылым болды және геометрия математиканың көптеген саласымен астасып жатады.

Геометрия - ерте замандарда шыққан ғылымдардың бірі, оның тарихы да әріректен басталады. Сапалық өзгерістерге ұшырап, жаңа сатыларға көтерілу дәрежесіне қарай геометрияның даму жолын төрт дәуірге бөлуге болады.

Бірінші дәуір өте ерте заман мен біздің заманымыздан бұрынғы 5 ғасыр аралығын қамтиды. Қарапайым геометриялық ұғымдар әр кезде және әр жерде шыққан. Алғашқы мәліметтер Ежелгі Шығыс елдерінде - Мысыр мен Вавилонда, Грекияда, кейінірек Үндістанда пайда болған. Ертедегі мысырлықтар Нілдің жағасындағы құнарлы топыраққа бидай егіп күнелткен. Ніл жыл сайын тасып, жағадағы телімшелердің белгіленген шекараларын бұзып кетіп отырған. Ал шаруалар су қайтқан сайын өз жерлерін өлшеп барып, айырып алатын болған. Телімшелердің ұзындығын, енін, жиек сызығын үнемі өлшеу нәтижесінде қарапайым ережелер пайда болған. Нілдің таситын және қайтатын уақыттарын бақылау нәтижесінде Мысыр күнтізбесі шыққан. Уақыт есебі жұлдыздардың өзара және көкжиекпен жасайтын бұрыштарын (бұл бұрыштардың төбелері бақылаушы тұрған жерде болады) өлшеуді қажет етеді. Мысыр патшалары - перғауындар (фараондар) өздеріне ескерткіш және зират ретінде, тірі күндерінде, зәулім құрылыстар - пирамидалар салдырған. Пирамида салу жұмыстары өлшеу әдістерін бірсыдырғы жүйеге келтіре отырып, кеңістіктік геометрия мен механиканың дамуына ықпал етті. Бізге жеткен математикалық папирустар Ежелгі Мысыр математикасының бертінгі ғасырларына жатады. Папирустардағы аудан мен көлем жөніндегі есептердің көпшілігі дұрыс шығарылған. Бірақ ережелердің ешқайсысы дәлелденбеген. Үшбұрыштың, трапецияның, дөңгелектің ауданы жуық түрде есептелген, табандары квадрат болып келген қиық пирамиданың көлемі дәл табылған. Ежелгі Вавилон геометриясының деректері балшықтан иленіп жасалған тақташаларға жазылып қалған. Оларға қарағанда ұзындық, аудан, көлем жөніндегі мысырлықтар білген есептерді вавилондықтар да шығара білген. Вавилондықтар кейбір дұрыс көпбұрыштарды, қиық конусты, т. б. қарастырған, шеңберді 360 градусқа бөлуді шығарған, есептерді теңдеулерге келтіруді жақсы білген, геометрияны астрономияға қолдана бастаған. Вавилондықтарға Пифагор теоремасы да белгілі болған. Кейбір геометриялық деректер Ежелгі Үндістан мен Қытайда да кездеседі.

Екінші дәуір - Евклидтен Рене Декартқа дейінгі кезең; ол екі мың жылға созылды. Евклид геометрияның өзіне дейінгі табыстарын жинап, талдап, қорытып, бір ізге түсіріп, біздің заманымыздан бұрынғы 300 ж. шамасында «Негіздер» атты, он үш бөлімнен құралған шығарма жазды. «Негіздерде» 121 анықтама, 5 қағида, 9 аксиома, 373 теорема келтірілген. Осы күнгі элементар геометрия, жалпы алғанда, Евклид қалыбынан шыққан. Геометрияға Архимед пен Аполлоний де ірі үлес қосты. Астрономиямен шұғылданған - Гиппарх, Клавдий Птолемей, Менелай, т. б. сфералық геометрия мен тригонометрияны қалыптастырды. Евклид, Архимед, Аполлоний заманы грек геометриясының «алтын ғасыры» болған еді. Орта Азия мен Қазақстан оқымыстыларынан геометриямен шұғылданғандар: Ғаббас әл-Жауһари, Әбу Наср әл-Фараби, Әбу Райхан әл-Бируни, Ғийас әд-Дин Жәмшид әл-Кәши, т. б. болды. Екінші дәуірдің аяғында геометрия Батыс Еуропада жандана бастады. Бұл кезде Иоганн Кеплер мен италия математигі Бонавентура Кавальеридің еңбектері тарихи белес болды.

Үшінші дәуір Рене Декарттан Николай Лобачевскийге дейінгі екі жүз жылды қамтиды. Бұл дәуірде аналитикалық, проективтік және дифференциалдық геометриялар пайда болды. Аналитикалық геометрия координаттар әдісіне сүйенеді. Онда нүктенің орны сандар арқылы, ал сызықтар мен беттер теңдеулер арқылы анықталады. Геометрияның бұл саласының іргесін Декарт пен француз математигі Пьер Ферма қалады, ал оны француз математигі Алекси Клеро мен Леонард Эйлер кемелдендірді. Фигураларды проекциялар арқылы түрлендіру жолдарын зерттеу нәтижесінде проективтік геометрия қалыптасты. Бұл бағытта француз математигі Жерар Дезарг, Блез Паскаль, француз математигі Жан Понселе, т. б. жемісті еңбек етті. Кеңістіктегі фигураны жазықтықта кескіндеу жолдарын талдап, француз математигі Гаспар Монж сызба геометрияны жасады. Сызба геометрия проективтік геометрияның тарауы болып саналады. Эйлер мен Монж дифференциалдық есептеу әдістерін геометрияға қолдана бастаған болатын. Карл Гаусс бұл мәселені одан әрі дамытып, классикалық дифференциалдық геометрияны қалыптастырды. Төртінші дәуір Лобачевский еңбектерінен басталады. Өз зерттеулерінде Лобачевский үш принципке сүйенді. Олар: Евклид геометриясы болуға тиіс және ол бірден-бір геометрия емес; аксиомаларды өзгертіп, жаңа геометрия жасауға болады; нақты кеңістікке қандай геометрия сәйкес келетіндігін тәжірибе көрсетеді. Лобачевский Евклидтің бесінші қағидасын (постулатын) өзінің басқа аксиомасымен (Лобачевский аксиомасы деп аталатын) ауыстырып, жаңа геометрия жасады. Бұл геометрияға Гаусс пен венгр математигі Янош Больяй да жақын келді. Бесінші қағида орнына өз аксиомасын (Риман аксиомасы деп аталатын) алып, Бернхард Риман эллипстік геометрияның негізін салды. Риман кеңістікті кез келген біртектес объектілер мен құбылыстардың үздіксіз жиыны ретінде түсіну қажеттігін көрсетті. Бұл идеяның құлашы кең болды. Соның арқасында кеңістіктің көптеген математикалық теориялары жасалды. Қазіргі геометрия, кеңістік пен фигураны жиын ұғымы арқылы анықтайды. Геометрия табиғатты зерттеуде, техниканы дамытуда қуатты құрал болып табылады. Ол математикалық анализге, механикаға, физикаға, астрономияға, геодезияға, картографияға, кристаллографияға, т. б. ғылымдарға елеулі ықпал етеді.

Көпбұрыштар ауданын оқытудың теориялық негіздері

Көпбұрыштар ауданын есептеудің ежелгі әдістері

Аудандарды есептеуге байланысты білім негіздері бұрынғы мыңжылдықтар үлесінде десек болады.

4-5 мың жылдар бұрын тіктөртбұрыштар мен трапециялар ауданын вавилондықтар квадрат бірліктерінде анықтаған екен. Аудан табуда квадраттың қызметі тамаша эталон болып табылады: Қабырғаларының теңдігі, тең және тік бұрыштары, симметриялылығы және жалпы формасының тамашалығы. Квадратты салу оңайлығы сонда, яғни жазықтықты бос орынсыз толтыру.

Ежелгі Қытайда ауданның өлшем бірлігі тіктөртбұрыш болды. Тасқалаушылар тікбұрышты үй қабырғасының ауданын анықтау үшін оның биіктігін еніне көбейтіп тапқан екен. Осыдан геометриядағы анықтама қабылданды: яғни тіктөртбұрыш ауданы оның сыбайлас қабырғаларының көбейтіндісіне тең. Мұндағы ең бірінші мәселе екі қабырғасы да бір өлшем бірлігінде анықталуы керек. Олардың көбейтіндісі тіктөртбұрыштың ауданын анықтайтын сәйкес квадрат бірлігінде болуы шарт. Егер биіктік пен ені дециметр бірлігінде болса, онда көбейтінді де бірдей өлшем бірлігінде болар еді. Егер қабырға қаптайтын Плоткалардың аудандарын қоссақ, қаптауға сәйкес қабырғаның саны анықталар еді. Бір -бірімен қиылыспайтын аудандарды табу үшін оларды қоссақ жеткілікті.

Ежелгі Египеттіктер 4000 жыл бұрын дәл осы қасиеттерді пайдаланып, тіктөртбұрыштардың ауданын табудың осы ережелерін пайдаланған, яғни үшбұрыш пен трапеция: табаны екіге бөлініп биіктігіне көбейтілген; трапеция үшін параллель қабырғаларының қосындысының жартысы биіктігіне көбейтілген және т. б. ; Қабырғалары 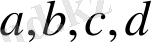болатын төртбұрыштың 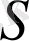ауданын табу үшін келесі формула қолданылған (1-сурет) :

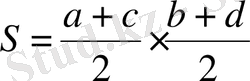(1. 1)

яғни қарама-қарсы қабырғаларының қосындысының жартысының көбейтіндісі.

1-сурет- Төртбұрыш

Бұл формула кез келген тіктөртбұрыш үшін қате болып табылады. Бұл формула бойынша барлық ромбтың ауданы бірдей болар еді. Ромб ауданына келсек оның төбелеріндегі бұрыштардың өлшеміне тәуелді болар еді. Берілген төртбұрыш ауданы тіктөртбұрыш үшін ғана дұрыс. Бұл формуланың көмегімен тіктөртбұрыштың ауданын немесе соған жақын тіктөртбұрыш ауданын табуға болады.

Тең бүйірлі үшбұрыш ауданын табу үшін египеттіктер үшбұрыш ауданын табу үшін 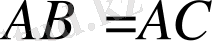болғанда

жуықтап келесі формуламен есептеді:

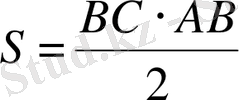(1. 2)

2-сурет-Тең бүйірлі үшбұрыш

Мұндағы қате азаюы, АВ мен АD айырмасынның азаюына тікелей байланысты, басқаша айтқанда В ( мен С) D табанының А -ға тұруынан. Сондықтан да (1. 2) формуласымен есептеу үшін төбедегі бұрыштың аздығына байланысты пайдаланылады.

Ежелгі гректер көпбұрыштар ауданын дұрыс есептеуді баяғыдан-ақ білді. Евклид өзінің «Бастамасында» «аудан» ұғымын «фигура» ретінде, яғни жазықтықтармен қоршалған, тұйық сызықтармен шектелген жазықтықтың бөлігін айтып өтті. Евклид аудан нәтижелерін санмен емес әртүрлі фигуралармен салыстырды.

Евклид ежелгі ғалымдар сияқты фигуралардың аудандарын басқа фигуралар, теңшамалы фигуралар аудандары арқылы қарастырды. Құрама фигураның ауданы өзгермейді деп есептелуі үшін оның аудандары қиылыспаса болды, дұрыс деп есептелді. Тіктөртбұрыш формуласымен бірге басқа фигуралар аудандарында іздеу арқылы табылды.

Сонымен үшбұрыш болса, оларды бірдей өлшемді төртбұрыштарға бөліп, содан соң ауданын тауып отырды. Осыдан үшбұрыш ауданы оның табанының жартысын биіктігіне көбейткенге тең болатындығы шықты. Осылай бөліктеп қою арқылы параллелеограмм ауданы табанының жартысы мен биіктігінің көбейтіндісінің жартысы, трапеция ауданы - табандарының қосындысының жартысы мен биіктігінің көбейтіндісіне тең. Тасқалаушылар күрделі қабырғаларды конфигурациялау үшін қабырға аудандарын анықтауда барлық қаптайтын плиткаларды қосып есептеу арқылы тапты. Кейбір плиткаларды кесіп, келтіру керек болды. Жұмысқа пайдаланылған барлық плиткаларды есептеп, торкөздерге бөліп, осылайша ауданды есептеген. Төркөздердің кішкентай болып бөлінуіне байланысты, яғни неғұрлым кішіреюіне байланысты ауданды табу мүмкіндігінше дәл есептелді.

Біздің заманымыздың бірінші ғасырында өмір сүрген Герон Александрийскийдің еңбектері басты қолданбалы сипатқа ие болуымен қатар, бұрынғы грек-математик-энциклапедистерінің бәрі болды. Ол мықты, сауатты инженер болуымен қатар, «Герон Механик» деген атқа ие болды. Герон өзінің «Диоптрика» деген еңбегінде түрлі машиналарды сипаттаумен бірге пратикалық өлшеу құралдарын да тапты.

Героннның кітаптарының бірі «Геометрика» деп аталды және онда формулалар жинағы мен сәйкес есептер болды. Онда квадраттар, тіктөртбұрыштар және үшбұрыштар ауданын табуға арналған мысалдар қарастырылды. Үшбұрыштың ауданын табуға байланысты Герон былай дейді: «Үшбұрыштың қабырғаларының өлшемі -13, 14, 15 болсын, Оның ауданын табу үшін 13+14+15=42, оның жартысы 21. 21 ден барлық үш қабырғаны шетінен алып тастасақ, яғни 21-13=8, 21-14=7, 21-15=6. 8*7*6*21=7056. Ал енді бәрін түбір астынан шығарсақ 84 - ке тең. Міне үшбұрыш ауданын осылайша есептеп табамыз».

«Метрика» деген еңбегінде Герон жоғарыда көрсеткен формуланы дәлелдеген:

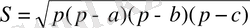, (1. 3)

мұндағы 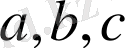‑ қабырғалары, 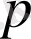‑ үшбұрыш периметрінің жартысы. Бүгінде бұл формула «Герон формуласы» деген атқа ие. Шындығында бұл формула б. з. д. 3 ғасырда өмір сүрген Архимедтің жаңалығы болып табылады. Герон ережесімен ауданды есептеудің практикалық формуласын ежелгі грек, рим және ортағасырлық жер өлшеушілер мен техниктер ұдайы пайдаланған.

1. 2 «Аудан», «Көпбұрыш» түсініктері, «Көпбұрыш ауданын» табудың әр түрлі тәсілдері

F фигурасының S(F) ауданы дегеніміз, фигураның ауданын құрайтын өлшем бірлігі. Десек те бұл анықтама емес, тек ауданды сипаттау десек болады. Оңай түсіну үшін қабырғалары 3 және 5 см болатын тіктөртбұрыштың ауданы дегеніміз 15 см квадрат болатын, 15 квадратқа бөлуге болады.

3-сурет-Тіктөртбұрыш

, а

Дөңгелек радиусы 2 см болатындай етіп құру үшін неше квадрат табу керек (4-сурет ) шындығында белгісіз

4-сурет

Ауданның қатаң математикалық анықтамасын мөлдір сеткадан тұратын квадраттары бар палетканы пайдаланып алуға болады. Палетканы жазықтықта жатыр деп елестетейік.

Басқаша айтқанда, жазықтық қабырғалары 1- ге тең квадраттарға бөлінген. Егер $F$ фигурасы толықтай фигураның ішінде жатса, мысалы 81 квадрат палеткада жатса, онда фигурада 43 квадрат бар деген сөз (5-сурет), яғни .

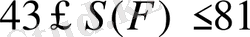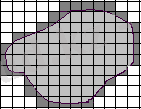
5-сурет

Мұғалім жеке көзқарасы бар, соны қорғай білетін жеке тұлға, зерттеушілік, ойшылдық қасиеті бар маман, білімді де білікті, көп оқыйтын, көп тоқитын, білімін күнделікті ісіне шебер қолдана білетін, өзінің оқушысын өз бетінше білім алуға үйрете білу керек.

ХХІ ғасыр - бұл техникасы күрлелескен, қоғамыдық қарым-қатынас шиленіскен қоғам айналадағы дүниеге, адамның денсаулығына, кәсіби мәдениеттілігіне мұқият қарайтын дәуір.

Бүгінгі білім мазмұны мұғалім мен оқушының арасындағы байланысты субьективті деңгейде көтерудегі демократиялық бастамалардың барлығы мұғалімдер арқылы жүзеге асырылады.

Бүгінгідей дамыған қоғамда, технологиялық күрделескен қоғамда бірғана тәсілмен өмір сүру, бір ғана шешім өте аздық етеді. Жән-жақтылы зерттеп, әртүрлі жолын білу қыйынды жеңілдетеді.

Көпбұрыштың анықтамаларын қарастырайық:

Анықтама: Барлық қабырғалары және барлық бұрыштары тең дөңес көпбұрышты дұрыс көпбұрыш деп атайды. Дұрыс n бұрыштың қабырғасын $a_{n}$ деп белгілесек, барлық қабырғалары тең болғандықтан, оның периметрі Pn = n• аn болады. Дұрыс n бұрыштың бұрыштары тең, ал барлық бұрыштарының қосындысы 180˚(n - 2) болғандықтан, оның әрбір бұрышы α болады.

1 - мысал.

Дұрыс он бесбұрыштың бұрышын есептеп табу керек. Шешуі. n = 15 деп алып, α формуласын пайдаланамыз. Сонда α = •180˚ = 156˚ Жауабы: $156^{{^\circ}}$

2 - мысал.

Бұрышы $144^{{^\circ}}$ болатын дұрыс n бұрыштың қабырғалар санын анықтау керек.

Шешуі: α формуласының көмегімен α = 144˚ деп алып, дұрыс

көпбұрыштың n бұрыштар санын табамыз: 144˚ =, n = 10 Жауабы: n = 10(он бұрыш)

1) бұрыштарының қосындысын;

2) әрбір бұрышын;

3) әрбір төбесіндегі сыртқы бұрышын;

4) бір төбеден шығатын диагональдар санын;

5) барлық диагональдарының санын

6) егер периметрі 24, 6 м болса, әрбір қабырғасын табыңдар.

Берілгені: Шешуі:

1) α=140˚ α = 1) 140˚ = n = 9

2) α=150˚ 2) 150˚ = n = 12 3) α=168˚

3) 168˚ = n = 30 n=?

Жауабы: 9; 12; 30.

Трапецияны шешу тәсілі

Мектеп оқушыларының геометриялық есептерді нашар шығаратыны белгілі. Оның бірнеше себебі бар. Біріншіден геометриялық есептер оқушылардан шығармашылық қасиеттерді талап етеді. Екіншіден оқушыларға берілетін теориялық мағлұматтар геометриялық есептерді шығаруды жеңілдететін жұмысшы құрал бола алмай тұр.

Жалпы геометрияда тіктөртбұрышты, ромбыны, квадратты параллелограмнан өрбітіп дамытады. Ал трапецияны « Екі қабырғасы параллель, ал былайғы екі қабырғасы параллель емес төртбұрыш трапеция деп және оның параллель қабырғалары (а, в) табандары, ал былайғы екі қабырғасы (с, d) бүйір қабырғалары деп анықтама беріледі. Трапецияның үш түрі болатындығы айтылады.

Жоғарыда айтылғандай трапецияны да тіктөртбұрышты, ромбыны, квадрат секілді параллелограмнан таратып, трапецияның параллелограмға ұқсас түрлерінен бастап, белгілі трапецияларды айтар болсақ, трапеция тақырыбының ауқымы арта түсері анық.

Осы орайда мектебімізде үйірме сабақтарында трапецияның оқулықтарда айтыла бермейтін түрлері мен қасиеттері үйретілген еді. Солардың бірі мынадай:

Теорема 1 . Тең бүйірлі трапецияның диагональдары өзара перпендикуляр болса, онда трапецияның орта сызығы биіктікке тең болады.

Дәлелдеуі: Трапецияның ауданы екі үшбұрыштың аудандарының қосындысына тең.

∆АОВ, ∆СОД-тең бүйірлі тікбұрышты үшбұрыштар АО ² + ОВ ² =а ² , 2АО ² =a ²

CO ² + OD ² =в ² , 2СО ² = в ² . АД=ВС

(*) формуласына қойсақ, онда

Трапецияның ауданы екеуін теңестіріп, бұдан

Теорема дәлелденді.

1. есеп №293 (B деңгей)

Бер:АВСД -тең бүйірлі трапеция.

АВ =24 см

ДС=40 см

АД┴ВС

т/к: S _ABCD

Шешуі : 1 теорема бойынша МN=ВК

S=32*32=1024см ²

Жауабы: S=1024 cм ²

Теорема 2. Кез келген трапецияның екі табанының қосындысы оның диагоналдарының үлкен табанға түсірілген проекцияларының қосындысына немесе айырмасына тең болады.

Оны формула түрінде берсек: а+в= d ¹ ₁ d ¹ ₂

Трапеция тең бүйірлі болғанда, оның диагональдары тең болатыны және диагональдарының үлкен табанға түсірілген проекциялары да тең болатыны белгілі. Трапецияның ауданын есептейтін формуласына қою арқылымына формула шығады. S= t*һ (1), мұндағы t- диагоналдың үлкен табанға түсірілген проекциясы, һ-трапецияның биіктігі.

2-есеп

Тең бүйірлі трапецияның диагоналы $10см$ -ге, ал ауданы $48{см}^{2}$ -ге тең. Трапецияның биіктігін табыңдар

Берілгені : $AC = 10см$ , $S = 48{см}^{2}$

Табу керек : $CH$

Шешуі: $\mathrm{\Delta}\ ACN$

AH Оны (1) формулаға қойып, теңдігі шығады. Бұдан

$\left( 100 - {CH}^{2} \right) *{CH}^{2} = 2304$ , ${CH}^{4} - 100{CH}^{2} + 2304 = 0\ \$ ${CH}^{2} = x$ деп алсақ, $x^{2} - 100x + 2304 = 0$

$x = 50$

$x_{1} = 36$ , $x_{2} = 64$ . Яғни, биіктік $6см$ және $8см$ .

3-теорема. Кез келген трапецияның диагональдарының квадраттарының айырмасы олардың үлкен табанға түсірілген проекцияларының квадраттарының сәйкес айырмасына тең болады.

Оны формула түрінде берсек: $\left( d_{1}^{2} - d_{2}^{2} \right) = \left( d_{1}' \right) - (d_{2}')$ (1. 4)

Математикалық есептерді шығару кезінде орындалатын дағдылар қажет болады: есептің берілгендеріне талдау жасау, бұрын өтілген есептермен салыстыру, қасиеттерді анықтау, қарапайым моделдерді құрастыру, ойша экспериментті іске асыру, біріктіру, есеп шығаруға қажетті ақпаратты таңдау, оны бір жүйеге келтіру, бұл ақпаратты қысқаша мәтін, символика, график түрінде тұжырымдап есеп шығаруға қолдану, есеп шешімін жалпылау, берілгендер арасындағы ерекше жағдайды зерттеу, есеп шығару кезінде осы заманғы психологияның жетістіктерін пайдалану.

Есептерді бір сыныптың әр оқушылары әр түрлі формада түсінеді. Математикаға қабілетті оқушы көпбұрыштың дербес элементтерін, біртұтас комплекстегі өзара байланысты элементтерді, комплекстегі әрбір элементтердің түсінеді. Орташа оқитын оқушы есептің дербес элементтерін ғана түсіне алады. Сондықтан көпбұрыштың ауданын шешуді үйреткен кезде есептегі қабырғалар, бұрыштар арасындағы қатысты арнайы талдау керек. Элементтер есептер шартын талдауға қажетті тәсілдерді таңдап алуға мүмкіндік береді. көпбұрыштың ауданын шығару кезінде көбінесе бұрын өтілгендерді еске түсіруге тура келеді. Қабілетті оқушы ең қажетті «жалпыланған, құрылымы қабаттасқан» ақпаратты есінде қалдырады. Есте сақталған ақпарат мида қалады, есте қалғандары пайдалануға жеңіл, оңай есте сақталады. Есептерді шешу кезіндегі жалпылау тек ойды дамытып қана қоймай, еске сақтауды да және «жалпыланған ассоциацияны» да қалыптастырады. Есеп шығару кезінде осылардың бәрін ескеру керек.

Ойлауды үйрену

Математикалық есептер мен жаттығулардың тиімділігі көбінесе оқушылардың есептер шешу кезіндегі шығармашылық белсенділігінің дәрежесіне тікелей байланысты. Есеп оқушылардың сабақтағы ойлау қызметін белсенді қалыпқа келтіреді. Есептер оқушылардың ойын оятып, оларды жұмыс істеуге, ойлауға бағыттайды.

Оқушылардың ойлау дағдысын дамыта отырып, дамуға - салу, түрлендіру, тұжырымдарды еске сақтау арқылы дәл ойлауға, талқылай білуге, айғақтарды қарастыра білуге, жалпы және жеке ой қорытындыларын жасауға үйренеді. көпбұрыштың ауданын табудың қанша тәсілдерің қарастыру арқылы ойлау қабілетнің ұшқырлығын дамытады.