Математика сабақтарында оқушылардың танымдық белсенділігін арттырудың жолдарын сипаттай отырып функция мәнін түсіндіру, оның ең үлкен және кіші амалдарын табу жолдарын зерттеу

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 20 бет
Таңдаулыға:

МАЗМҰНЫ

Кіріспе
3
І
Функция деген не, функцияның анықталу облысы
5
1.1
Функцияның берілу тәсілдері
7
1.2
Функция ұғымын анықтау
8
ІІ
Функцияның ең үлкен және ең кіші мәндері
12
2.1
Тұйық облыстағы функцияның ең үлкен және ең кіші мәндері
12
2.2
Функцияның берілген кесіндідегі ең үлкен және ең кіші мәндерін табу тәсілдері

15
III
Тәжірибелік-эксперименттік жұмыс бөлімі
20
3.1
Функцияның ең үлкен және ең кіші мәндері
20

Қорытынды
24

Пайданылған әдебиеттер тізімі
25

Kipicпe

Тәуелсіз мемлекетіміздің ертеңі ұрпақтың рухани байлығы мәдениеті, саналы ұлттық ойлау қабілеті мен біліміне, іскерлігіне байланысты.
Осы орайда егеменді еліміздің білім беру жүйесінде әлемдік деңгейге жету үшін жасалынып жатқан талпыныстар оқытудың әр түрлі әдіс-тәсілдерін қолдана отырып терең білімді, ізденімпаз, барлық іс-әрекеттерінде шығармашылық бағыт ұстанатын, сол тұрғыда өз болмысын таныта алатын жеке тұлға тәрбиелеу ісіне ерекше мән берілуде. Демек, мектептегі оқу үрдісі оқушылардың танымдық белсенділігін арттырып, шығармашылық әрекетін дамытуына жол ашуы қажет.
Математика пәнінің білім стандарты - Қазақстан Республикасындағы жалпы білім беретін мектептің бастауыш сатысындағы барлық түрлеріне ортақ математикадан оқушылардың алатын міндетті (минимум) білім деңгейін тағайыдайтын құжат.
Математика пәні бойынша бастауыш білім стандартындағы білім мазмұнын оның құрылымын анықтау төмендегідей ұстанымдарды ескеру арқылы жүзеге асырылады:
- Ізгілендіру;
- Интеграция;
- Дидактикалық бірліктерді ірілендіру.
Математика да өнер сияқты таным әдісі. Оқушының таным әрекетін жақсарту үшін, ойын-сауықтардың, қызықты сұрақтардың, жұмбақтардың, мақал-мәтелдердің математикалық негізін біліп, оларды тұжырымдауда қолданылатын математикалық тілдерді меңгеріп, оқиғаны өмірмен байланыстырып, оның тәрбиелік мәнін ашып отыру қажет. Мұны математика пәнінің мазмұны да, оқу бағдарламасы да талап етеді. Көптеген зерттеу жұмыстары мен мектептегі озат тәжірибелерді баспа бетінде жариялау мұны мойындағанымен, оқыту үрдісінде қалай пайдалануға болатындығына нақты материалдың жоқтығы мәселені қиындата түседі. Біздің зерттеуіміздің теориялық та, практикалық та маңызы бар.
Математика күрделі пән болу үстіне, ол ақыл-ой оралымдылығына, әлем бірлігін түсінуге қызмет етеді. Математиканы оқытудың тәрбиелік мәні мен практикалық мазмұны математиканы мектепте оқытудың білім беру мақсатымен ұштасып жатады.
Математикалық білім стандартында математикалық білім, білік, дағдыларды игеру, танымдық және коммуникативтік іс-әрекет пен өздігінен білім алуға, еңбекке бейімдеу, оқушының ақыл-ойының математикалық стилін, интеллектуалдық және ерік пен сезімге қатысты сапаларын дамыту көзделген. Сондай-ақ ата-дәстүр, әдет-ғұрып, салт-сана, халықтың және ұлттың болмысты дүниежүзілік мәдени мұраларын үндестіру, меңгерген математикалық білімдерін өмірде қолдануға жан-жақты дайындау арқылы баланы жеке тұлға етіп қалыптастыруға басымдық берілген.
Танымдық белсенділік - оқушының оқуға, білуге деген ынта-ықыласының, құштарлығының ерекше көрінісі. Танымдық белсенділік проблемалық сұрақтың жауабын іздестіруде, өзіндік жұмыс орындауда жүзеге асады.
Оқушының өздігінен білім алуы өз еркімен жүйелі жұмыс істеуді талап етеді. Өздігінен білім алуды оқушылардың күнделікті рухани қажетіне айналдыру мәселесіне мән берілмей келеді. Өздігінен білім алу әрекеттің мақсат-міндеттерін, мазмұнын, ұйымдастыру жолдарын оқушылардың өздері анықтап, іске асыруына байланысты. Ал оларға кеңес, нұсқау, жалпы бағыт беріп, басқарып отыру - мұғалімнің міндеті.
Осы міндеттен бастауыш мектеп мұғалімінің оқушылардың танымдық белсенділігін арттыру жолында оқытуды тиімді ұйымдастыру үшін оның теориялық негізін, қолданыс алысын және практикада пайдаланудың жолдарын игеру қажеттілігі туындайды. Бұл біздің алып отырған зерттеу жұмысымыздың тақырыбының өзектілігін көрсетеді.
ЗЕРТТЕУ МАҚСАТЫ: Математика сабақтарында оқушылардың танымдық белсенділігін арттырудың жолдарын сипаттай отырып функция мәнін түсіндіру, оның ең үлкен және кіші амалдарын табу жолдарын зерттеу
ЗЕРТТЕУ МІНДЕТТЕРІ:Осы аталған мақсаттан туындайтын міндеттер:
- Функция деген не, функцияның анықталу облысы;
- Функцияның берілген кесіндідегі ең үлкен және ең кіші мәндерін табу тәсілдері.
- Озық педагогикалық тәжірибені жинақтау, талдау.
ЗЕРТТЕУ ПӘНІ - математикалық анализ:

1 Функция деген не, функцияның анықталу облысы

Функция (cәйкестік) анықтамасы: X және Y жиындары берiлсiн. Егер X және Y жиындарының арасындағы f сәйкестiгi бойынша X жиынының әрбiр элементiне Y жиынының бiр ғана элементi сәйкес қойылса, f сәйкестiгiн X жиынынан Y жиынына бейнелеу деп аталады. Белгiлеуi: f: X--Y. Егер y элементi f бейнелеуi бойынша x элементiнiң бейнесi болса, оны f(x) = y теңдiгi арқылы жазамыз. Мұндағы x элементi y элементiнiң f бейнелеуі бойынша алғашқы бейнесi, ал y элементi x элементiнiң бейнесi деп аталады (сурет-1).

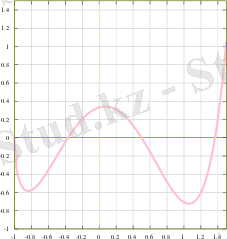
1-Сурет - Функция графигі

Егер X мүмкін мәндер жиынтығынан алынған х-тің әрбір мәніне айнымалы Y жиынының белгілі бір мәні у сәйкес келсе, онда у айнымалы шамасы х айнымалы шамасының функциясы деп аталады. Мұндай тәуелділік у=f(х) түрінде жазылады. f әрпінің орнына басқа әріптер де (мыс., F, т.б.) қолданылады. Мұндағы х-ті тәуелсіз айнымалы (кейде аргумент) деп, ал оның өзгеру облысы (жиыны) у-тің анықталу облысы деп аталады. х-тің өзгеруіне байланысты айнымалы у-тің қабылдайтын мәндерінің жиынын у функциясының өзгеру облысы деп атайды.

Функцияның жоғарыда берілген анықтамасында назар аударатын екі жағдай бар:
- біріншісі - аргумент х-тің өзгеру облысын көрсету;
- екіншісі - х пен у мәндерінің арасындағы сәйкестік ережені немесе заңды тағайындау. Егер х-тің бір мәніне у-тің бір ғана мәні сәйкес келсе, онда у-ті х-тің бір мәнді функциясы деп, ал егер х-тің бір мәніне у-тің бірнеше мәні сәйкес келсе, онда у-ті х-тің көп мәнді функциясы деп атайды.
Айнымалы шамалар (х пен у) мәндерінің арасындағы сәйкестік ережені немесе заңды функц. тәуелділік дейді. Функция көбінесе аналитикалық тәсіл немесе формула арқылы (мысалы, т.б.), кейде графиктік және таблицалық (дәл не жуық формулалармен есептелген) тәсілдерімен де беріледі. Математиканың одан әрі дамуы нәтижесінде Функция табиғаты кез келген айнымалы математикалық объектілер арасындағы сәйкестік ретінде жалпыланды. Математиканың басқа ұғымдары тәрізді Функция ұғымы да бірден қалыптасқан жоқ. Ол дамудың ұзақ жолынан өтті. "Функция" термині алғаш рет 1692 ж. Г. Лейбництің еңбектерінде кездесті. Функцияның қазіргі ұғымға жақын алғашқы анықтамасын И. Бернулли (1718) берген, ал бұл ұғымды Д. Бернулли, Л. Эйлер, Ж. Фурье, П. Дирихле, Н. И. Лобачевский, т.б. одан әрі дамытты.
Функция дегеніміз - бір айнымалыға басқа бір айнымалының бір мәнің сәйкес қоятын тәуелділік, заң. Мысалы: y = x + 1 функциясы әрбір x-ке y-тің x+1 мәнің сәйкес қояды.
x = 0 болса, y = x+1 = 0+1 = 1,
x = 1 болса, y = x+1 = 1+1 = 2 тағы сол сияқты.

1.1 Функцияның берілу тәсілдері

F=x--Y функциясы берілсін. Егер x және y жиындарының элементтері нақты сандар (яғни, XᴗR) болса, f функциясы сандық функция деп аталады. Әрі қарай сандық функцияларды қарастырамыз және қысқаша функциялар деп атап, y=f(x) арқылы белгілейтін боламыз. X айнымалысы функцияның аргументі немесе тәуелсіз айнымалы, ал у-функция немесе тәуелді айнымалы (х-тан) деп аталады. х және у шамаларына қатысты, олардың функционалдық тәуелділікте екендігі айтылады. Кейде у-тың х-тан функционалдық тәуелділігін жаңа (f) әрпін енгізбей-ақ, y=y(x) арқылы да белгілейді.
y=f(x) функциясының x=a болғандағы дербес шешімі f(a) арқылы белгіленеді. y=f(x) функциясын беру үшін, х арқылы у-тың мәні табылатындай ережені көрсету қажет. Функцияны берудің аналитикалық, кестелік, графикалық тәсілдері жиі кездеседі.
Аналитикалық тәсіл: функция бір немесе бірнеше формулалар немесе теңдеулер арқылы беріледі.
y= f(x) функциясының анықталу облысы көрсетілмеген жағдайда формуланың мағынасы болатындай аргументтің барлық мәндерінің жиынымен сәйкес келеді.
Графиктік тәсілмен берілуінің артықшылығы оның көрнектілігінде, ал кемшілігі - нақты еместігінде.
Кестелік тәсіл: функция аргумент мәндерінің және сәйкес функция мәндерінің кестесі түрінде беріледі. Мысалы, тригонометриялық функциялардың мәндерінің кестесі, логарифмдік кестелер.
1) D жиынында анықталған y=f(x) функциясы жұп деп аталады, егер ѧx℮D үшін - x ϵ D және f (-x) =f(x) шарттары орындалса, ал - x ϵ D және f (-x) =f(x) шарттары ѧx ϵ D үшін орындалса функция тақ деп аталады. Жұп функция графигі Oq осіне, ал тақ функция графигі координата басына қарағанда симметриялы
2) y= f(x) функциясы D жиынында анықталған болсын және D1 ϵ D. Егер кез-келген x1, x2 ϵ D1 аргументтерінің мәндері үшін x1x2 болғанда f (x1) f (x2) теңсіздігі орындалса, онда функция D1 жиынында өспелі деп аталады; D1 жиынында өспелі, өспейтін, кемімелі, кемімейтін функциялар осы жиында монотонды деп аталады, ал өспелі және кемімелі функциялар қатаң монотонды функциялар деп аталады. Функция монотонды болатын интервалдар монотондық интервалдары деп аталады. Суретте (жоғарыда) көрсетілген функция (-2; 1) және (3; 5) интервалында қатаң монотонды, (1; 3) интервалында монотонды.

1.2 Функция ұғымын анықтау

Функция аса маңызды математикалық ұғымдардың бірі және де ол заттар мен құбылыстардың өзара байланысын бейнелейді.
Бүгінде функцияны анықтаудың әр түрлі жолдары белгілі. Солардың бірінде функция ұғымы бастапқы ұғым ретінде алынады.
Енді бірінде бастапқы ұғым ретінде бейнелеуді алалды да, функция деп бір X жиынын екінші Y жиынына бейнелеуді түсінеді. Бұл жайдайда xєX элементпен yєY болатын, бір және тек бір ғана элемент жұптүзей алынатына ерекшеленеді. Сонда функцияны белгілеп көрсету үшін ʃ, φ, ψ және т.с.с. символдар пайдаланады. Ал X жиыны функцияның анықталу облысы және Y жиынын функцияның мәндерінің облысы деп атайды.
Анықталу облысы X және мәндерінің облысы Y болатын ʃ (x) функцияны символдар арқылы мына түрде X -- Y немесе айнымалылырдың көмегімен xxєx--yyєy деп белгілейді, сонда функция мәнінің белгісі ү-тің орнына ʃ символын жиі қолданады. Бұл жайдайда ункцияны x-- ʃ (x) түрінде белгілейді. Кейде x жиыны элементтерін функцияның аргументі деп атады да, ʃ -ті аргумент x-тің немесе анымалы x-тің функциясы дейді.
Бейнелеулер, қатынастар және сәйкестіктер табиғаты әр түрлі жиындарда берілуі мүмкін екендігі белгілі, ендеше олардың дербес түрі болып табылатын функцияның да анықталу облысы мен мәндерінің облысы әр түрлі жиындар бола алады.
Ал математика курсында негізінен сандық және нүктелік жиындар қарастырылады, өйткені осы жиындарда функцияның әр түрлі қасиеттерін қарастыру өте қолайлы.
X және Y қандай да бір сандық жиындар болсын XR, YR.
Анықтама. X жиынында анықталған, ал мәндері Y жиынында болатын сандық функция деп әрбір xєX санына бір ғана yєY санын сәйкес қоятын ʃ сәйкестікті айтады.
Сандық функцияны негізінен x-- ʃ(x), ʃ xєX немесе y = ʃ (x) түрінде белгілейміз. Сонда сандық X жиыны - ʃ функциясының анықталу облысы, ал (x) түріндегі барлық сандардан тұратын, мұндағы xєX, сандық Y жиыны ʃ -тің мәндерінің жиыны болып табылады.
Және де ʃ функциясының анықталу облысын D (ʃ) арқылы; ал оның мәндерінің жиының Е (ʃ) арқылы да белгілейді.
Функцияны көрсетіп беру үшін сандық X жиынды және әрбір xєX санына сәйкес келетін y санын, яғни функцияның мәнін табу үшін қолданылатын тәсілді көрсетіп беру керек болады.
Жалпы алғанда, егер әрбір xєX санына қанда да бір y саны сәйкес қойылса, онда XR жиынында сандық функция берілген дейді. Сонда әрбір y = ʃ (x), xєX функциясымен, оның мәндерімен тұратын, яғни ʃ (x), xєX, сандық YR жиыны байланысты болады.

Функцияны әр түрлі тәсілмен анықтап береді. Соның ішінде ең көп тарағы - функцияның аналитикалық тәсілмен берілуі, яғни аргументтің мәні бойынша функцияның сәйкес мәнін табу кезінде орындалатын амалдардың жиынтығын көрсететін формула арқылы функцияның берілуі. Сонда функцияның анықталу облысы көрсетіледі. Егер формула арқылы берілген функцияның анықталу облысы айқын түрде көрсетілмесе және ешқандай қосымша шектеулер келтірілмесе онда функцияның анықталу облысы, айнымалының осы формуланың мән-мағынасы болатындай барлық мәндерінен тұрады.
Функцияны аргументтің мәндері және функцияның сәйкес мәндері арасындағы сәйкестік заңын сөз арқылы сипаттаудың келтіруімен де анықтап беруге болады. Осындай функциялар үшін арнайы таңбалардың да енгізілуі орынды. Мысалы: y=[x], xєR, мұндағы {x}=x-{x}, x санының бөлшек бөлігі.
Функцияны, оның графигі деп аталатын, координаттық жазықтың қандай да бір сызығының көмегімен анықтап беруге болады. Жалпы алғанда, әрбір функциямен қандай да бір сызық - осы функциның графигі байланысты. Алайда бұған кері ұйғарым әрдайым тура бола бермейді, өйткені xєX болатын x-тің берілген мәнінде оған сәйкес келетін функцияның бір ғана мәні y бар болады.
Сондықтан ордината осіне параллель жүргізілген әрбір түзуде функцияның графигіне тиісті бірден артық болмайтын нүкте ғана жатуы тиіс. Мәселен, шеңбер қанда да бір функцияның графигі болып табылмайды, өйткені шеңбердің екі нүктесі жататын ордината осіне параллель түзулер бар.
Жалпы алғанда y= ʃ(x), xєX функциясының графигі деп xєX ал y= ʃ(x) болатын (x; y) парлардың; яғни (x , ʃ (x)), xєX түріндегі парлардың жиынын айтады. Осындай реттелген әрбір парға координаттық жазықтықтың абсциссасы x және ординатасы y= ʃ (x) бір ғана нүктесі сәйкес келеді. Ендеше координаттық жазықтықтың дәл осындай нүктелерінің жиыны y= ʃ (x), xєX функциясының графигін кескіндейді.
Кейбір жағдайларда, аргументің таңдап алынған мәндерінде функцияның мәндерін табуға мүмкіндік беретіндей кесте құруға болады. Осындай кестелердің мысалдары ретінде сандардың квадраттарының және кубтарының кестелерін, тригонометриялық функциялар мәндерінің кестелерін және т.б. атаған жөн. Әсіресе, X жиыны шектеулі болса, онда айнымалылардың сәйкес мәндерінің кестелерін пайдаланған тым қолайлы. Бұл жағдайда функция кестелік тәсіл арқылы анықтап берілген болып табылады.
Дегенмен функцияның аналитикалық және графигтік тәсілдермен берілуі оны оқып-үйренуге өте қолайлы. Осыған орай, аналитикалық тәсілмен берілетін нақты функцияларды анықтайық.
Біз оларды мынадай ретпен оқып-үйренеміз:
А) қандай да бір функцияға киліктіретін, яғни оны енгізу себепші болатын нақты жағдайларды қарастырамыз;
Ә) функцияның анықтамасын тұжырымдаймыз және оны формуламен анықтап береміз де, осы формуланың құрамындағы параметрлерді зерттейміз;
Б) оқып-үйренетін функцияны график арқылы кескіндеп көрсетеміз;
В) функцияның кейбір касиеттерін қарастырамыз.
Тура пропорционалдық, оның қасиеттері және графигі.
t - жаяу адамның қозғалыс уақыты, s - оның жүрген жолы және ол v кмсағ жылдамдықпен бірқалыпты қозғалыста болсын делік. Сонда v тұрақты болғанда t-ның әрбір мәніне s-тің бір ғана мәні келеді және ол s= v∙ t формуласымен есептеледі. Сондықтан s= v·t формуласы, тура пропорционалдық, яғни s дегеніміз t-ға тура пропорционал, деп аталатын функцияны анықтап береді.
Анықтама. Тура пропорционалдық деп y=kx формуласын, мұндағы, x тәуелсіз айнымалы, ал k0 және kєR, көмегімен берілетін функцияны айтады.
Бұл формула айнымалы y-тің айнымалы x-ке тәуелділігін, яғни анымалы y-тің анымалы x-ке тура пропорционал екендігін анықтап береді, мұндағы k - пропорционалдық коэффициент.
Егер функциясы 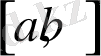кесіндісінде үзіліссіз және 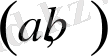аралығында дифференциалданатын болса, онда
немесе ,
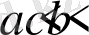
теңдігі орындалатындай 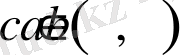нүктесі табылады. Бұл теңдік Лагранж формуласы деп аталады.
Егер қисығының АВ доғасының барлық нүктесінде жанамасы бар болса, онда қисықтың ең болмағанда бір нүктесі бар болып, осы нүктедегі қисықтың жанамасы АВ хордасына параллель болады. (2-сурет)
Лагранж формуласын былай тұжырымдауға болады: функция өсімшесі аралық нүктедегі туындының мәні мен аргумент өсімшесінің көбейтіндісіне тең.
Лагранж теоремасы арқылы өсімшелердің теоремасы деп аталады. Егер 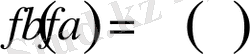болса, онда (2)-ден 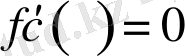болады, яғни Ролль теоремасы Лагранж теоремасының дербес жағдайы.
(Жозеф-Луи Лагранж (1736-1813) - француз математигі және механигі).
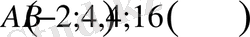1-мысал. параболасының нүктелері берілген.
Жанама АВ хордасына параллель болатындай АВ доғасынан С нүктесін табу керек.
Шешуі. [-2;4] кесіндісінде берілген 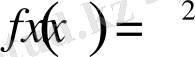функциясы Лагранж теоремасының шарттарын қанағаттандырады.
Шарт бойынша:
Берілгендерді (2) Лагранж формуласына қойып, мыналарды аламыз:

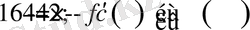
Бұдан, 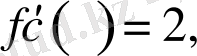мұндағы
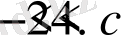
Берілген функцияның туындысының болғандағы мәнін анықтаймыз:
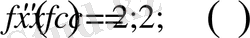бұдан,
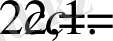
Сонымен, C (1;1) нүктесінде жанама АВ хордасына параллель болады.
у В

Т у

1
А С
С
0 х 0 1 с е х

3-сурет 4-сурет
2-мысал. Лагранж формуласы бойынша 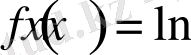функциясы үшін 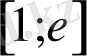кесіндісінде с-тың мәнін анықтау керек.
Шешуі. Берілгені бойынша:
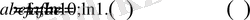
Сонда
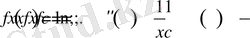
(2) формула бойынша мынаны аламыз:
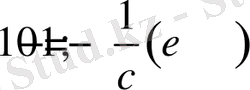бұдан

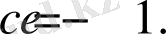
2 Функцияның ең үлкен және ең кіші мәндері

Іс жүзінде белгілі бір аралықтағы функцияның ең үлкен және ең кіші мәндерін табуға тура келетін есептер жиі кездеседі.
Егер функция [a,b] кесіндісінде үздіксіз болса, онда ол осы кесіндіді өзінің ең үлкен (ең кіші) мәнін қабылдайды. Бұл жағдайда сол кесіндідегі функцияның ең үлкен (ең кіші) мәні f(x) функциясының (a,b) интервалында жататын дағдарыс нүктелерінің бірінде қабылдайтын мәніне немесе кесіндінің шеткі нүктелерінің бірінде қабылдайтын мәніне тең.
Бұдан [a,b] кесіндісінде f(x) функциясының ең үлкен немесе ең кіші мәндерін табуға болатын төмендегідей ереже шығады:
1) [a,b] кесіндісінде жататын дағдарыс нүктелерін табамыз және функцияның осы нүктелердегі мәнін есептейміз.
2) f(x) функциясының [a,b] кесіндісінің соңғы нүктелеріндегі мәндерін, яғни f(a)-ны және f(b)- ны табамыз.
3) Функцияның осы табылған мәндерін салыстырамыз, оның ең үлкені функцияның берілген кесіндідегі ең үлкен мәні болады да, ең кішісі ең кіші мәні болады.

2.1 Тұйық облыстағы функцияның ең үлкен және ең кіші мәндері

Z = f (x, y) функциясы тұйық Ḏ облысында анықталған және үзіліссіз болсын. Функция осы Ḏ облысының ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.