ЖАРЫҚ ЖЫЛДАМДЫҒЫ

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 10 бет
Таңдаулыға:

ЖАРЫҚ ТОЛҚЫНДАРЫ

ЖАРЫҚ ЖЫЛДАМДЫҒЫ

Геометриялық оптикада жарық сәулелерінің бағыты ғана зерттеледі. Жарықтың таралу процесінің уақытқа байланысты қалай өтетіні жөніндегі мәселе геометриялық оптика көлеміне кірмейді. Жарықтың қасиеті және оның затпен өзара байланысы физикалық толқындық оптикада толығырақ қарастырылады. Біз бұл тарауды жарық жылдамдығын қалай өлшегені жөніндегі әңгімеден бастаймыз.

Қосқышты басып қалсақ, жарқ етіп бөлме іші жарыққа толады. Жарықтың қабырғаларға жетуіне уақыттың мүлде керегі жоқ сияқты. Жарық жылдамдығын анықтау үшін толып жатқан тәжірибелер жүргізілген. Ол үшін жарық сигналының алыс ара қашықтықтарға (бірнеше километрге) таралу уақытын дәл сағатпен өлшемек болған. Бірақ бұдан еш нәтиже шықпады. Жарықтың таралуына мүлде уақыт кетпейді, жарық қандай ара қашықтыққа болсын лезде жетеді деп ойлайтын болды. Алайда олай емес, жарықтың жылдамдығы шектеулі болып шықты, ақырында ол жылдамдық та өлшеңді.

Жарық жылдамдығын өлшеудің астрономиялық тәсілі. Жарық жылдамдығын алғаш рет 1676 жылы дат ғалымы О. Рёмер өлшеді. Рёмер астроном болған, оның өлшеген жарық жолы - өте ұзақ болды, табысқа жетуіне себепші болған да сол еді. Ол жол - күн жүйесіндегі планеталардың ара қашықтығы.

Рёмер күн жүйесіңдегі ең үлкен Юпитер планетасы серіктерінің тұтылуын бақылады. Юпитердің Жерден өзгешелігі сол, оның он серігі бар. Рёмер олардың ең жақынын - Ио серігін бақылады. Ол Ионың Юпитер алдынан қалай өткенін, содан кейін оның көлеңкесіне кіріп, көзден қалай ғайып болғанын көрді. Сонан соң ол лезде жарқ еткен шам тәрізденіп, қайта көрінді. Осы екі от алудың уақыт аралығы 42 сағ 28 минутқа тең болып шықты. Сөйтіп, бұл "ай", әрбір тең уақыт аралығында Жерге сигнал жіберіп тұратын, үлкен аспан сағаты болып шықты.

Алғашқыда өлшеу жұмыстары, Жер өзінің Күңді айнала қозғалысында Юпитерге ең жақын келген кезде жүргізілді (92-сурет) . Бірнеше айдан соң дәл осыңдай өлшеулер Жер Юпитерден қашықтағыңда жүргізілген, осындай өлшеулер ойламаған жерден, Ионың белгілі айналу периоды бойынша есептеп шығаруға болатьш серіктің көрінетін уақыт мезетімен салыстырғанда, серіктің көлеңкеден 22 минут кешігіп шыққанын көрсетті.

Рёмер мұны былай түсіндірді: "Егер мен Жер орбитасының екінші жағында тұратын болсам, онда әр жолы Ио белгіленген уақыт та көлеңкеден шығып отырар еді. Бұл жағдайдағы кешігу менің алғаш бақылаған жерім мен қазір тұрған орныма дейінгі ара қашықтықты жарықтың өтуіне кеткен 22

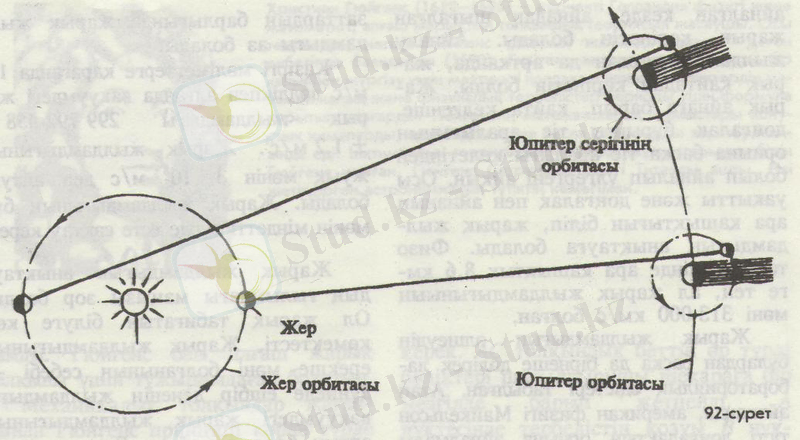
минутта болып отыр". Ионың кешігіп көрінген уақытын, соған сәйкес ара қашықтықты біліп, осы ара қашықтықты кешіккен уақытқа бөліп, жылдамдықты табуға болады. Жылдамдық аса зор шама болып шықты, шамамен 3 км/с ¹ . Соңдықтан да Жер бетіндегі алыс деген екі нүкте арасында жарықтың таралу уақытын білу аса қиын. Жарық бір секундта Жер экваторының ұзындығынан 7, 5 есе артық ара қашықтықты жүріп өтетіні белгілі.

Жарық жылдамдығын өлшеудің лабораториялық әдістері. Жарық жылдамдығын лабораториялық әдіспен 1849 жылы алғаш рет өлшеген француз физигі - И. Физо.

Физо тәжірибесінде жарық көзінен шыққан жарық линза арқылы өтіп, жартылай мөлдір пластинаға (1) түседі (93-сурет) Пластинадан шағылғаннан соң фокусталған жіңішке шоқ тез айналатын тісті доңғалақтың тістерінің арасына бағытталады. Тістердің арасынан өткен жарық доңғалақтың бірнеше километр арақашықтықтағы айнаға (2) түсірілді. Айнадан шағылған жарық бақылаушының көзіне түсуден бұрын қайтадан доңғалақ тістерінің арасынан өтуі тиіс еді. Доңғалақ жай айналған кезде, айнадан шағылған жарық

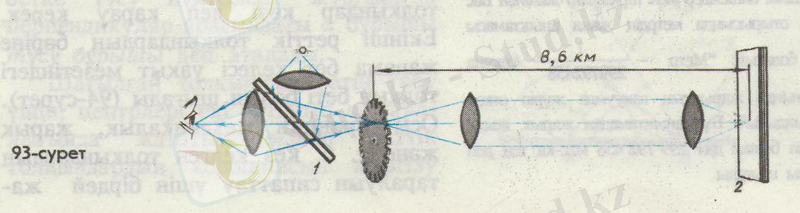
көрінетін болады. Айналу жылдамдығы одан да артқанда, жарық қайтадан көрінетін болды. Жарық айнаға барып, қайта келгенше, доңғалақ бұрынғы тіс аралығының орнына басқа тіс аралығы келетіндей болып айналып үлгергені айқын. Осы уақытты және доңғалақ пен айнаның ара қашықтығын біліп, жарық жылдамдығын анықтауға болады. Физо тәжірибесінде ара қашықтық 8, 6 км-ге тең, ал жарық жылдамдығыныың мәні 313 000 км/с болған.

Жарық жылдамдығын өлшеудің бұлардан басқа да бірнеше дәлірек лабораториялық әдістері табылған. Атап айтқанда, американ физигі Майкельсон тісті доңғалақтың орнына айналмалы айналар қолданып, жарық жылдамдығын өлшеудің жетілген әдісін тапты.

Жарық жылдамдығы түрлі мөлдір денелердің ішінде өлшенеді. Су ішіндегі жарық жылдамдығы 1856 жылы өлшеңді. Вакуумге қарағанда, судағы жарық жылдамдығы 4/3 есе аз болады. Вакуумге қарағанда, басқа

заттардың барлығында жарық жылдамдығы аз болады.

Қазіргі мәліметтерге қарағанда 1, 2 м/с дәлдікпен алғаңда вакуумдегі жарық жылдамдығы 299 792 458 ± ±1, 2 м/с ¹ . Жарық жылдамдығының жуық мәнін 3 • 10 ⁸ м/с деп айтуға болады. Жарық жылдамдығының бұл мәнін міндетті түрде есте сақтау керек.

Жарық жылдамдығын анықтаудың ғылымдағы маңызы зор болды. Ол жарық табиғатын білуге көп көмектесті. Жарық жылдамдығының ерекше мәні болғанының себебі - дүниеде ешбір дененің жылдамдығы вакуумдегі жарық жылдамдығының артық бола алмайды. Бұл - салыстырмалық теориясы шыққаннан кейін айқын болды, ол теория туралы келесі тарауда айталады.

Жарықтың шағылу және сыну заңдарын толқындардың жай-күйін сипаттайтын ортақ бір принциптен шығарып алуға болады. Бұл принципті алғаш Ньютонның замандасы Христиан Г ю й г е н с ұсынған еді.

Гюйгенс принципі бойынша ортаның ұйытқу барып жеткен әрбір нүктесі екінші реттік толқындардың көзі болып шығады. Толқын бетінің I уақыт мезетіңдегі орнын табуды біле түра, оның келесі і + Дг уақыт мезетіндегі орнын табу үшін, толқын бетінің әрбір нүктесін екінші реттік толқындар көзі деп қарау керек. Екінші реттік толқындардың бәріне жанама бет келесі уақыт мезетіндегі толқын беті болып шығады (94-сурет) . Осы принцип механикалық, жарық және т. б. кез келген толқындардың таралуын сипаттау үшін бірдей жарамды.

Христиан Гюйгенс (1629-1695) - көрнекті Голландия физигі және математигі, алғаш жарықтың толқындық теориясын жасаушы. Осы теорияның негізін Гюйгенс „Жарық жайында трактат" деген еңбегінде баяндайды (1690) . Гюйгенс ең апғаш рет сағатты бір қалыппен жүргізу үшін маятникті қолданды және маятниктердің ма тематикалық және физикалық тербелістер периоды үшін формула қорытып шығарды. Гюйгенстің математикалық жұмыстары конустық қималарды, циклоидты және басқа қисықтарды зерттеу жай ында еді. Ықтималдық теорисының алғашқы жұмыстарының бірін Гюйгенс жазған. Гюйгенс Сатрунның серігі Титанды ашты. Өзі жетілдірген астрономиялық түтіктің көмегімен.

Гюйгенс оны алғаш жарық толқыны үшін тұжырымдаған болатын.

Механикалық толқындар жағдайында Гюйгенс принципі көрне түрде түсіндіріледі: тербелістер барып жеткен ортаның бөлшектері, өз кезегінде, тербеле отырып, ортаның өзара әсерлесетін көршілес бөлшектерін қозғалысқа келтіреді.

Шағылу заңы. Гюйгенс принципінің көмегімен, екі ортаның шекара бетінен шағылған толқындар бағынатын заңды қорытып шығаруға болады.

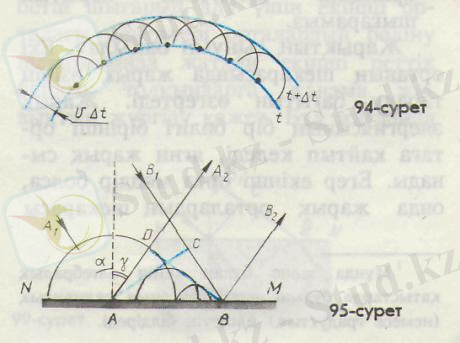
Жазық толқынның қалай шағылатынын қарастырайық. Егер фазалары тең бет (толқыңдық бет) жазық болса, онда толқын жазық толқын деп аталады. 95-суретте ММ шағылдырушы бет, А/А және ВІВ - түскен жазық толқынның екі сәулесі (олар бір-біріне параллель) . Ал АС жазықтығы - осы толқынның толқындық беті.

Түскен сәуле мен шағылдырушы бетке түсу нүктесінде жүргізілген перпендикуляр арасындағы а бұрышы түсу бұрышы деп аталады.

Шағылған толкынның бетін табу үшін, центрлері екі ортаның шекаралығында жататын екінші реттік толқындардың қоршамасын жүргізу

керек. АС толқындық беттің әр түрлі беліктері шағылдырушы шекараға бір мезгілде барып жетпейді. А нүктесінде тербелістің қозуы В нүктесіндегіден

t = CB/v уақыттан ерте басталады (мұндағы v - толқын жылдамдығы),

Толқын В нүктесіне жетіп, осы нүктеде тербеліс қоза бастаған мезетте, центрі А нүктесінде болатын екінші реттік толкындық радиусы

r = АD =vt = СВ жарты сфера болып шығады. Сонда А мен В нүктелерінің арасында орналасқан көздерден тараған екінші реттік толқыңдардың радиустары 95-суретте көрсетілгендей болып өзгереді. Екінші реттік толқындардың қоршамасы - сфералық беттерге жанама болып

келген ВВ жазықтығы. Ол шағылған толқынның толқын беті болып табылады. Шағылған АА ₂ және ВВ ₂ сәулелер DВ толқын бетіне перпендикуляр. Сонда шағылдырушы бетке перпендикуляр мен шағылған сәуле арасындағы у бұрышы шағылу бұрышы деп аталады.

Ал АD = СВ және АDВ мен АСВ тікбұрышты үшбұрыштар болғандықтан, DВА = САВ. Бірақ қабырғалары өзара перпендикуляр бұрыштар болғаңдықтан, а = САВ және у = DВА.

Ендеше, шағылу бұрышы түсу бұрышына тең:

а = у. (5. 1)

Сонымен қатар, толқынды Гюйгенсше салудан мынадай қортынды шығады: түскен сәуле, шағылған сәуле, және түсу нүктесіне тұрғызылған перпендикуляр бір жазықтықта жатады. Бұл екі

тұжырым жарықтың шағылу заңы болып табылады.

Егер жарық сәулелерінің таралу бағытын ауыстырсақ, онда шағылған - сәуле түскен сәуле, ал түскен сәуле шағылған сәуле болып шығады. Жарық сәулелер жолының қайтылымдығы - олардың маңызды қасиеті.

Шағылу заңына негізделген жазық айнада кескін салу ережесі VIII сыныпта қарастырылған.

Кез келген толқынның жоғарыда тұжырымдалған жалпы таралу принципі - Гюйгенс принципі. Бұл принцип қарапайым геометриялық салулар көмегімен алдыңғы мезеттегі белгілі толқындық бет бойынша келесі мезеттегі толқындық бетті табады. Гюйгенс принципінен толқындардың шағылу заңы қорытылған.

ЖАРЫҚТЫҢ СЫНУ ЗАҢЫ

Жарықтың сыну құбылысы дегеніміз не екенін еске түсірейік. Жарықтың сыну заңын Гюйгенс принципі көмегімен қорытып шығарамыз.

Жарықтың сынуын бақылау. Екі ортаның шекарасында жарық өзінің таралу бағытын өзгертеді. Жарық энергиясының бір бөлігі бірінші ортаға қайтып келеді, яғни жарық сынады. Егер екінші орта мөлдір болса, онда жарық орталардың шекарасы арқылы жарым-жартылай өте алады, мұнда да әдеттегідей таралу бағытын өзгертіп отырады. Бұл құбылыс жарықтың сынуы деп талады.

Сыну салдарынан нәрселердің пішіндері олардың орындары мен өлшемдері өзгерген сияқты болып көрінеді. Мөлдір емес бос стаканның түбіне тиын немесе кішірек бір нәрсе салайық. Тиын ортасы, стаканның шеті және көз бір түзудің бойында орналасатындай етіп стаканды қозғайық. Енді осы қалпымызды бұзбай, стаканға су құяйық. Судың деңгейі көтерілген сайын стаканның түбі тиынмен бірге көтеріліп келе жатқандай болады.

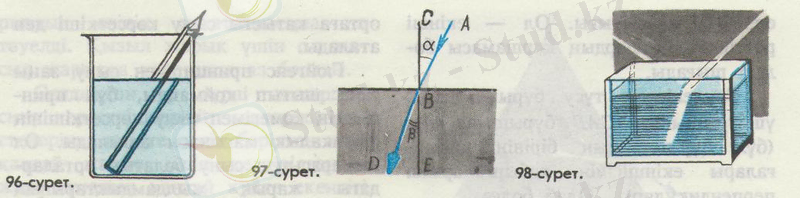
Алғашында жартылай ғана көрінген тиын енді бүтіндей көрінетін болады. Су құйылған әйнек ыдысқа көлбете қарындаш салып қояйық. Егер осы ыдысқа бүйірінен қарасақ, қарындаштың суға батып тұрған бөлігі әрегірек жылжып кеткен сияқты көрінеді (96-сурет) .

Бұл құбылыстар екі ортаның шекарасында сәуленің бағыты өзгеретіндігімен жарықтың сынатындығымен түсіндіріледі.

Жарықтың сыну заңы АВ түскен сәуле (97-сурет), ВВ сынған сәуле және орталарды бөліп тұрған бетке түсу нүктесінен тұрғызылған перпендикуляр өзара қалай орналасатынын анықтайды: а бұрышы - түсу бұрышы, ал в бұрышы сыну бұрышы деп аталады.

Түскен, шағылған және сынған сәулелерді жіңішке жарық шоғын көрінетіндей егіп түсіріп, бақылау қиын емес. Мұндай жарық шоғының ауадағы жолын, ауаға аздап түгін жіберіп немесе экраңды бұрыш жасай орналастырып, байқауға болады. Сынған шоқ флюресцеинмен боялған аквариумдағы судан да көрінеді (98-сурет) .

Жарықтың сыну заңын қорыту. Жарықтың сыну заңы XVII ғасырда тәжірибие жүзіңде тағайындалғанды. Біз оны Гюйгенс принципі көмегімен қорытып аламыз. Жарықтың бір ортадан екінші ортаға өткенде сынуы екі ортаның әрқайсысында жарықтың әрбасқа жылдамдықпен таралуы салдарынан болады. Толқынның бірінші ортадағы жылдамдығын vi, ал екінші ортадағы жылдамдығын vi арқылы белгілейік.

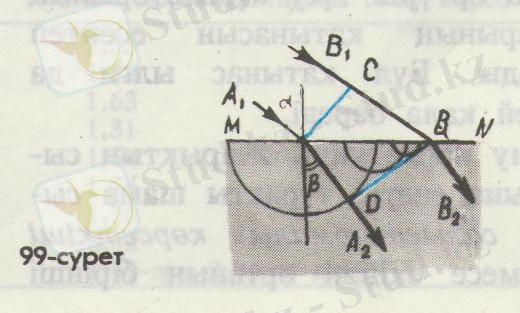
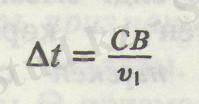Айталық, екі ортаны бөліп тұрған жазық шекараға (мысалы, ауадан суға өтетін бөліну шекарасына) жарықтың жазық толқыны келіп жетті дейік (99-сурет) . АС толқындық бет А\А мен В\В сәулелерге перпендикуляр. ММ бетке алдымен А\А сәуле келіп жетеді. В\В сәуле ол бетке

уақыттан кейін келіп жетеді. Сондықтан екінші реттік толқын В нүктесінде қоза бастаған мезетте А нүктесінен шыққан толқын радиусы

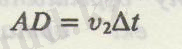
сфера түріне еніп үлгіреді.

Сынған толқынның толқындық бетін шығарып алу үшін екінші ортадағы центрлері орталардың бөліну шекарасында жатқан екінші реттік барлық толқындарға жанама жазықтың жүргізу қажет. Бұл жағдайда

ол ВD жазықтығы. Ол - екінші реттік толқындардың қоршамасы болып шығады.

Сәуленің а түсу бұрышы АВС үшбұрышының САВ бұрышына тең (бұл бұрыштардың бірінің қабырғалары екіншісінің қабырғаларына перпендикуляр) . Олай болса,

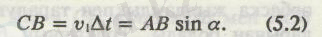
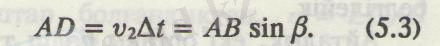в сыну бұрышы АВD үшбұрыштың АВD бұрышына тең. Сондықтан

(5. 2) теңдікті (5. 3) теңдікке мүшелеп бөліп, мынаны табамыз

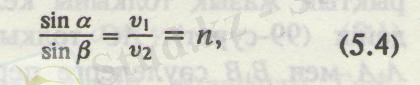
Мұндағы п - тұрақты шама, түсу бұрышына тәуелді емес.

99-суреттен көріп отырғанымыздай, түскен сәуле сынған сәуле және түсу нүктесіне туғызылған перпендикуляр бір жазықтықта жатады. Осы айтылған ұйғарым мен түсу бұрышының син-сының сыну бұрышының синусына қатынасы екі орта үшін де тұрақты шама болады дейтін (5. 4) теңдеуді біріктіргенде жарықтың сыну заңын береді.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.