Натурал сандар туралы

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 194 бет
Таңдаулыға:

Натурал сандар
§1. Натурал сандарды оқу және жазу

Заттарды санау үшін немесе қандай да бір заттың біртекті заттар
арасындағы реттік нөмірін көрсету үшін пайдаланылатын 1, 2, 49, 854, ...
сандары натурал сандар деп аталады.
0 натурал санға жатпайды.
Ондық санау жүйесінде кез келген натурал сан 0, 1,2, 3, 4, 5, 6, 7, 8
және 9 цифрларының көмегімен жазылады. Мысалы, 2457 санының жазылуы 2 -
мыңдықтар цифры, 4 - жүздіктер цифры, 5 - ондықтар цифры және 7 - бірліктер
цифры екенін білдіреді, яғни

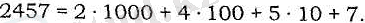
Жалпы, егер a - мыңдықтар цифры, b - жүздіктер цифры, с - ондықтар
цифры және d - бірліктер цифры болса, онда

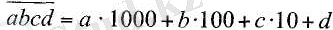
санын аламыз. Сондай-ақ, қысқаша 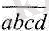жазылуы пайдаланылады.
Натурал сандарды оқу үшін:
1) натурал санды оң жағынан бастап әрбір класы үш цифрдан тұратындай
кластарға бөлу қажет;
2) әр кластағы санды үлкенінен бастап оқып, оған кластың атауын қосып
оқу керек; барлық бірліктері нөл цифрынан тұратын кластың атауы оқылмайды.
Кластар атауы: триллиондар (трлн), миллиардтар (млрд), миллиондар
(млн), мындықтар (мың), бірліктер (бір).
069 000 003 125 800. .
(трлн млрд млн мық бір)
Бұл сан былай оқылады: 69 триллион 3 миллион 125 мың 800.
Мысалы, 6080000047 санын оқу үшін, үш цифрлы кластарға бөлеміз: 6 080
000 047; ал оқығанда ең үлкен кластан бастап әр кластағы санға кластың
атауы қосылып оқылады:
6 миллиард 80 миллион 47.
Мыңдық кластың (кластағы сан 000 болғандықтан) және бірлік кластың
жүздігі оқылмайды.
Санның жазылуы ең үлкен кластан басталады. Одан соң кейінгі кластағы
сан жазылады және бұл реттілік бірлік кластармен аяқталады. Сандарды
жазғанда (үлкен кластан басқа) әрбір класта үш цифрдан болуы қажет,
жетіспейтін цифрлардың орнына нөл жазылады.
Мысалы, 23 триллион 7 миллион 8 санын жазу үшін, үлкен разрядтағы сан
триллиондардан (023 немесе 23 санының өзін) бастаймыз, келесі класс -
миллиард саны, бұл класс ескерілмегендіктен үш нөл (000) жазамыз, келесі
класс - 7 миллион (007); мындықтар класы ескерілмегендіктен (000); соңғы
класс бірліктер 8, яғни (008).
Сонымен жоғарыдағы сан мына түрде жазылады:
023 000 007 000 008.
§2. Натурал сандарды қосу, азайту және салыстыру

Екі натурал санды қосудың нәтижесі әрқашанда натурал сан болады: егер
а, b натурал сандар болса, онда с = a + b - натурал сан, а мен b -
қосылғыштар, с - қосынды деп аталады.
Қосудың қасиеттері (бұл қасиеттер кез келген сандар үшін орындалады).
1) Кез келген екі қосылғыштың орындарын ауыстыруға болады (қосудың орын
ауыстырымдылық қасиеті):
m + п = п + т.
2) Үш қосылғыштың қосындысын табу үшін алдымен бірінші және екінші
қосылғыштардың қосындысын табуға немесе екінші және үшінші қосылғыштардың
қосындысын табуға болады (қосудың терімділік қасиеті):
m + n + k = (m + n) + k = m + (п + k).
3) Санға нөлді қосқанда, қосынды сол санның өзі болады:
m + 0 = 0 + m.
а + b = с шартын қанағаттандыратын b саны с және а сандарының с - а
айырымы деп аталады. с - а = b болған жағдайда, с - азайғыш, a - азайтқыш,
b - айырым деп аталады.
Мысалы, 71 және 28 сандарының айырымы дегеніміз - 28-ге сол айырымды
қосқанда 71 болатын сан.
71 - 28 = 43, сонымен қатар 28 + 43 = 71.
Натурал сандарды қосу және азайту амалдары ең кіші разрядтан басталып
орындалады.

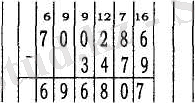
Натурал сандарды салыстыру үлкен разрядтан бастап разрядтар бойынша
жүргізіледі. Мысалы, 2871 2829. Мұнда мыңдық және жүздік разрядтар тең,
ал ондық разрядтар тең емес: 7 2.

§3. Натурал сандарды көбейту және бөлу

Екі натурал санды көбейтудің нәтижесі әрқашан натурал сан болады: егер
a, b натурал сандар болса, онда с = a · b - натурал сан, а және b —
көбейткіштер, с - көбейтінді деп аталады.
Көбейтудің қасиеттері (бұл қасиеттер кез келген сандар үшін
орындалады).
1) Кез келген екі көбейткіштің орындарын ауыстыруға болады (көбейтудің
орын ауыстырымдылық қасиеті):

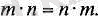
2) Үш көбейткіштің көбейтіндісін табу үшін, алдымен бірінші және екінші
көбейткіштердің көбейтіндісін табуға немесе алдымен екінші және үшінші
көбейткіштердің көбейтіндісін табуға болады (көбейтудің терімділік
қасиеті):

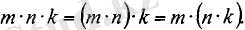
3) Кез келген санды 1-ге көбейткенде, көбейтінді сол санның өзіне тең:

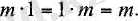
4) Кез келген санды нөлге көбейткенде, көбейтінді нөл болады:

а санын 6-ға бөлгендегі бөліндіден b - с = а шартын қанағаттандыратын с
санын атайды.
а : b = с болған жағдайда a - бөлінгіш, b - бөлгіш, с - бөлінді деп
аталады.
а санын b санының еселігі, ал b санын а санының бөлгіші деп те атайды.
Мысалы, бөлінді анықтамасы бойынша 22:11 дегеніміз - 11-ге көбейткенде
22 болатын сан.
22 : 11 = 2,өйткені 2 · 11 = 22;
0 : 22 = 0, өйткені 22 · 0 = 0.
Санды нөлге бөлуге болмайды!
Бөлудің қасиеттері (бұл қасиеттер кез келген сандар үшін орындалады).
1) Егер бөлінгіш пен бөлгішті қандай да бір нөлге тең емес бірдей санға
көбейтсе, бөлінді өзгермейді. Мысалы:
66 : 2 = (66 • 3) : (2 • 3) = 33.
2) Бөлінгішті қандай да бір a · 0 санына көбейтіп, бөлгішті өзгеріссіз
қалдырсақ, онда бөлінді a ece артады. Мысалы:
(66 · 3) : 2 = (66 : 2) · 3 = 33 · 3.
3) Белгішті қандай да бір a · 0 санына көбейтіп, бөлінгішті өзгеріссіз
қалдырсақ, онда бөлінді a ece кемиді.
Мысалы:
66 : (2 · 3) = (66 : 2) : 3 = 33 : 3 = 11.
Егер сандық өрнекте жақшалар болмаса, онда алдымен көбейту және бөлу
амалдары, содан кейін қосу мен азайту амалдары орындалады.
Егер сандық өрнекте жақшалар болса, онда алдымен жақша ішіндегі амалдар
орындалады.
Мысалы, 5-318-312 : (2+ 4) өрнегінің мәні былай есептеледі:
1) 2 + 4 = 6;
2) 5-318 = 1590;
3) 312 : 6 = 52;
4) 1590 – 52 = 1538.
Көбейтудің қосу амалына қатысты үлестірімділік қасиеті:
а, b және с сандары үшін (а + b)с және ас + bс өрнектерінің мәндері
бірдей:
(а + b)с = ас + bс.
Көбейтудің қосу амалына қатысты улестірімділік қасиетін келесі түрде
пайдалануға болады.
(а + b) · с өрнегін ас + bс өрнегімен ауыстыруға болады. Мұндай
ауыстыру жақшаны ашу амалы деп аталады. Мысалы:
201 · 135 = (200+ 1) - 135.
Өрнек (а + b) – с түрінде, мұндағы a = 200, b = 1, с = 135. Жақшаны
ашсақ:
(200 + 1) · 135 = 200 · 135 + 1 · 135 = 27135.
Егер өрнек a · c + b · c түрінде болса, онда оны (а + b) · с өрнегімен
ауыстыруға болады. Мұндай ауыстыру ортақ көбейткішті жақша сыртына шығару
амалы деп аталады.
Мысалы,
1287·31+ 713·31
өрнегі а·с + b·с түрінде, мұндағы а = 1287, b = 713, с = 31.
Бұл өрнекті (а + Ь) · с өрнегімен ауыстыруға болады, онда ортақ
көбейткіш 31 жақша сыртына шығарылады: 1287 · 31 + 713 · 31 = (1287 + 713)
· 31 = 2000 · 31 = 62 000.
т + 714·т өрнегі a·c + b·c түрінде, (а + b) ·с түріне де жатпайды.
Бірақ т = 1 · т екенін ескерсек, осы өрнекті былай жазуға болады: 1 ·
т + 714 · т дегеніміз - а·с + b·с түріндегі өрнек, мұндағы a = 1, b = 714,
с = т. Бұл өрнекті (а + b) · с түрінде жазып, ортақ көбейткіш т-ды жақшаның
сыртына шығаруға болады:
1 · т + 714 · т = (1 + 714) · m = 715 · т.

§4. Жай және құрама сандар

Қандай да бір берілген санды қалдықсыз бөлетін натурал сандардың бәрі
осы санның бөлгіштері деп аталады.
Егер санның тек екі бөлгіші (санның өзі және бір) ғана бар болса, онда
ол жай сан деп аталады. Мысалы, 7 - жай сан, өйткені оның екі бөлгіші бар
(1 және 7).
Егер санның екіден көп бөлгіштері бар болса, онда ол құрама сан деп
аталады. Мысалы, 100 - құрама сан, өйткені оның бөлгіштерінің саны екіден
көп (1, 2, 4, 10, 100 және т.с.с).
1 санының бір ғана натурал бөлгіші бар, ол - 1 саны. Сондықтан 1 саны
жай санға да, құрама санға да жатпайды.
Кез келген құрама санды жай сандардың көбейтіндісі түрінде жазуға
болады.
Құрама санды жай сандардың көбейтіндісі түрінде жазуды құрама санды жай
көбейткіштерге жіктеу деп атайды.
Мысалы, 90 = 2 · 3 · 3 · 5.

§5. 2, 5 және 10-ға бөлінгіштік белгілері

0, 2, 4, 6, 8 цифрлары және осы цифрлармен аяқталатын сандар жұп сандар
деп аталады. 1, 3, 5, 7, 9 цифрлары және осы цифрлармен аяқталатын сандар
тақ сандар деп аталады. Жұп цифрлар 2-ге бөлінеді, ал тақ цифрлар 2-ге
бөлінбейді.
2, 5 және 10 сандарына бөлінгіштік белгілері санның соңғы цифрына
қатысты тағайындалады.
1) Егер қандай да бір санның соңғы цифры 2-ге бөлінетін болса, онда осы
сан 2-ге қалдықсыз бөлінеді.
2) Егер қандай да бір санның соңғы цифры 5-ке бөлінетін болса, онда осы
сан 5-ке қалдықсыз бөлінеді.
3) Егер қандай да бір санның соңғы цифры 10-ға бөлінетін болса, онда
осы сан 10-ға қалдықсыз бөлінеді.
Мысалы, 78 394 100 саны 2, 5 және 10-ға қалдықсыз бөлінетін 0 цифрымен
аяқталады. Демек, бұл санның өзі 2, 5 және 10-ға қалдықсыз бөлінеді:

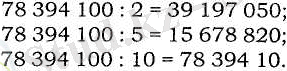
385 624 саны 2-ге бөлінетін, ал 5 пен 10-ға қалдықсыз бөлінбейтін 4
цифрымен аяқталады. Демек, бұл санның өзі 2-ге бөлінеді, бірақ 5 пен 10-ға
бөлінбейді:

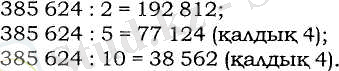
§6. 3-ке және 9-ға бөлінгіштік белгілері

3-ке және 9-ға бөлінгіштік белгілері санның цифрлары қосындысы бойынша
анықталады.
1) Егер цифрларының қосындысы 3-ке қалдықсыз бөлінетін болса, онда осы
санның өзі де 3-ке қалдықсыз бөлінеді.
2) Егер цифрларының қосындысы 9-ға бөлінетін болса, онда осы санның өзі
де 9-ға қалдықсыз бөлінеді.
28 551 саны цифрларының қосындысы:
2 + 8 + 5 + 5+1 = 21.
21 саны 3-ке қалдықсыз бөлінеді, сондықтан 28 551 саны да 3-ке
қалдықсыз бөлінеді.
21 саны 9-ға қалдықсыз бөлінбейді, соңдықтан 28 551 саны да 9-ға
қалдықсыз бөлінбейді.

Ондық белшектер
§7. Ондық бөлшектерді оқу және жазу

Бірлік разрядтың оң жағында тағы да разряд кездесетін болса, онда
мұндай сандар ондық бөлшектер деп аталады. Ондық бөлшектерді жазғанда
бірлік разряд пен оның оң жағында тұрған разрядтардың қасына үтір жазылады.
Ал калькуляторда үтірдің орнына нүкте қойылады.
Үтірдің оң жағында ондық разрядтар орналасады, ал сол жағында ондық
бөлшектің бүтін бөлігі орналасады.
Ондық разрядтар ондық, жүздік, мыңдық, он мыңдың, жүз мыңдық,
миллиондық, жүз миллиондық және т.с.с. аталады.
0 және кез келген натурал санды бірлік разрядтан кейін үтір жазып,
үтірден кейін нөлдер тіркеп жазу арқылы ондық бөлшек түрінде жазуға болады:
0 = 0,000; 783 = 783,00.
Үтір (калькуляторда нүкте) ондық бөлшекті екі бөлікке бөледі: үтірдің
сол жағында бүтін бөлігі, оң жағында бөлшек бөлігі орналасады.
Ондық бөлшекті оқу үшін:
1) бүтін бөлігін оқып шығып, бүтін сөзін қосу керек;
2) бөлшек бөлігін оқып шығып, кіші разрядтың атауын қосып айту керек.
Мысалы, 3,07 бөлшегі үш бүтін жүзден жеті деп оқылады. 0,037 бөлшегі
нөл бүтін мыңнан отыз жеті деп оқылады.
Ондық бөлшекті жазу үшін:
1) бүтін бөлігін жазып, үтір қою керек;
2) бөлшек бөлігін соңғы цифры қажетті разрядқа келіп түсетіндей етіп
жазамыз.
Мысалы, 31 бүтін мыңнан 8 бөлшегі 31,008 түрінде жазылады.

§8. Ондық бөлшектерді салыстыру

Ондық бөлшектерді салыстыру ережесі
Бүтін бөліктері әр түрлі екі ондық бөлшектің қайсысының бүтін бөлігі
кем болса, сол бөлшек кіші болады, ал қайсысының бүтін бөлігі артық болса,
сол бөлшек үлкен болады. Мысалы, 31,9567 37,3. Бүл бөлшектердің бүтін
бөлігі тең емес: 31 37.
Бүтін бөліктері бірдей екі бөлшекті салыстыру үшін оң жақтан нөлдер
тіркеп жаза отырып, екі бөлшектің үтірден кейінгі ондық таңбаларының санын
теңестіріп, олардың бөлшек бөлігін салыстыру қажет.
Мысалы, 8,6 мен 8,59 сандарын салыстырайық. Бұл сандардың бүтін
бөліктері тең. Бірінші бөлшекте үтірден кейін бір цифр бар, ал екінші
бөлшекте екі цифр бар. Сондықтан бірінші бөлшекке оң жағынан бір нөл тіркеп
жазамыз, сонда 8,60 болып шығады. Ал 60 жүздік үлес 59 жүздік үлестен артық
болғандықтан, 8,60 8,59 және 8,6 8,59.

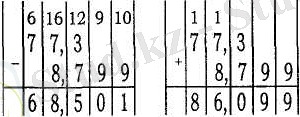
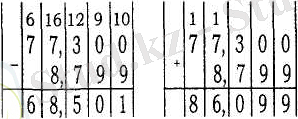
§9. Ондық бөлшектерді қосу және азайту

Ондық бөлшектерді қосу үшін:
1) қосылғыштардағы үтірден кейінгі таңбалардың санын теңестіру керек;
2) бірдей разрядтар бірінің астында бірі, ал қосылғыштарды бірінің
астына бірін келтіріп жазу керек;
3) бөлшектерді натурал сандарды қосқандағыдай етіп қосу керек;
4) шыққан қосындының үтірін қосылғыштардағы үтірлердің астына келтіріп
қою керек.
Ондық бөлшектерді азайту үшін:
1) азайғыш пен азайтқыштағы үтірден кейінгі таңбалардың санын теңестіру
керек;
2) үтірдің астына үтірді тура келтіріп, азайғыштың астына азайтқышты
жазу керек;
3) азайтуды натурал сандарды азайту амалымен орындау керек;
4) шыққан айырымда үтірді азайғыш пен азайтқыштағы үтірлердің астына
келтіріп қою керек. Мысалы,

§10. Дөңгелектеу

Ондық бөлшекті қандай да бір разрядқа дейін дөңгелектеуде разрядтан
кейінгі келесі цифрлардың барлығын нөлдермен алмастырады, ал ол цифрлар
үтірден кейінгі цифрлар болса, онда оларды алып тастайды. Егер бұл
разрядтан кейінгі бірінші келесі цифр 5, 6, 7, 8 немесе 9 болса, онда
қалдырылған соңғы цифрды 1-ге арттырады. Егер бұл разрядтан кейінгі бірінші
келесі цифр 0,1,2,3 немесе 4 болса, онда қалдырылған соңғы цифр өзгермейді.
4874, 3429 сандарын ондыққа дейін дөңгелектейік.

Жауабы. 4870.

0,995031 санын жүздікке дейін деңгелектейік.

Жауабы. 1,00.
§11.Шамалау

Есептеу нәтижесін, дөрекі бағалауды шамалау деп атайды.
Шамалау келесі түрде жүзеге асырылады:
1) сандағы барлық цифрлар нөлден өзгеше бір цифр қалғанға дейін
дөңгелектелінеді;
2) дөңгелектеу арқылы алынған сандарға көрсетілген амалдарды қолданып,
күткен нәтижені аламыз;
3) дөңгелектелінбеген сандарға да көрсетілген амалдарды қолданып,
шыққан санды күткен нәтижемен салыстырамыз. Егер бұл сандар жақын болса,
онда есептеудің дұрыс болғаны, егер бұл сандар алшақ болса, есептеу қайта
жүргізіледі.

§12. Ондық бөлшектерді 10, 100, 1000-ға т.с.с.-ға көбейту және бөлу

Ондық бөлшекті 10, 100, 1000-ға және т.с.с-ға көбейткенде, сан артады,
үтір оңға жылжиды.
Ондық бөлшекті 10, 100, 1000-ға және т.с.с.-ға бөлгенде, сан азаяды,
үтір солға жылжиды.
10, 100, 1000 және т.с.с. сандарда неше нөл болса, үтір сонша оңға
(солға) жылжиды.
Мысалы, 31,28-ді 1000-ға бөлгенде, келесі жайды аңғару керек
31,28 : 1000 31,28.
Үтір солға жылжиды. 1000-да үш нөл болғандықтан, үтір үш разрядқа солға
жылжиды. Демек
31,28: 1000 = 0031,28: 1000 = 0,03128.
0,03128 · 100 көбейтіндісін тапқан кезде келесі жайды аңғару керек
0,03128 · 100 0,03128.
Үтір оңға жылжиды. 100-де екі нөл болғандықтан, үтір екі разрядқа оңға
жылжиды. Демек
0,03128 · 100 = 3,128.

§13. Ондық бөлшектерді көбейту

Ондық бөлшектерді көбейту үшін келесі мәселелердің ескерілуі қажет:
1) көбейткіштердегі үтірлерді алып тастап, көбейткіштердің неше есе
артқанын ойда сақтау қажет;
2) шыққан натурал сандарды көбейту керек;
3) натурал сандардың көбейтіндісін әрбір көбейткіш қанша есе артса,
сонша есе азайту қажет.
Мысалы, 0,132 және 0,301 ондық бөлшектерінің көбейтіндісін табайық.

Жауабы. 0,132 · 0,301 = 0,039732. Бұл сан болатын нәтижеге жақын.
13,2 және 0,301 сандарын бағана бойынша көбейтейік.

Жауабы. Шамалаудың нәтижесіне жақын.
Немесе ондық бөлшектерді көбейткен кезде берілген сандарды, үтірлерге
көңіл аудармай (натурал сандар сияқты) көбейту жеткілікті, содан кейін
көбейткіштерде үтірден кейін (қоса есептегенде) оң жағынан сонша цифрды
үтірмен ажырату керек.
Мысалы, 2,7-ні 1,3-ке көбейтейік. Сонда 27 · 13 = 351 оң жағынан
үтірмен екі цифрды (көбейткіштердегі үтірден кейінгі цифрлардың қосынды
саны екіге тең) ажыратамыз. Нәтижеде 2,7 · 1,3 = 3,51.
Егер көбейтіндіде цифрлар саны үтірмен ажыратуға керек цифрлар санынан
аз болса, онда алдыңғы жағынан жетіспейтін цифрлар орнына нөлдер жазылады.
Мысалы:

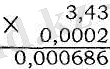
§14. Ондық бөлшекті натурал санға бөлу. Арифметикалық орта

Есеп. Ұзындығы 8,31 м болатын мата кесіндісі тең үш бөлікке бөлінген.
Әр бөліктің ұзындығын табыңыз.
Шешуі: Есепті шешу үшін мата ұзындығын сантиметр арқылы өрнектеу керек:
8,31 м = 831 см.Онда 831 : 3 = 277. Демек әрбір бөліктің ұзындығы 277 см,
яғни 2,77 м. Ал 2,77 саны 8,31 және 3 сандарының қатынасы деп аталады. Егер
2,77 санын 3-ке көбейтсек, 8,31 санын аламыз:

2,77 санын метрді сантиметрге айналдырмай-ақ алуға болады. Ол үшін
үтірге назар аудармай-ақ бөлуді орындап, бүтін бөлікте бөлу амалын орындап,
үтірді қоюға болады:

Егер бүтін бөлік бөлгіштен кіші болса, онда нәтижедегі бүтін бөлік
нөлден басталады, яғни бүтін бөлік нөл болады. Мысалы:

Тексеру:
0,54 · 4 = 2,16; 0,504 · 5 = 2,52; 0,097 · 12 = 1,164. Жай бөлшекті
ондық бөлшекке айналдыру бөлу амалы арқылы жүзеге асырылады. Мысалы,
бөлшегін ондық бөлшек түрінде жазайық.
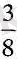дегеніміз 3 санын 8-ге бөлу болып табылады, олай болса бөлуді
орындайық:

Демек
Берілген бірнеше санның арифметикалық ортасын табу үшін осы сандарды
қосып, қосындыны қосылғыштар санына бөлу керек. Мысалы, 52,3, 61,2, 63,
54,7 сандарының арифметикалық ортасын табайық:
52,3 + 61,2 + 63 + 54,7 = 231,2; 231,2 : 4 = 57,8.

§15. Ондық бөлшекке бөлу

Ондық бөлшекті ондық бөлшекке бөлу үшін:

1) бөлгішті үтірсіз алып, бөлгіштің неше есе артқанын анықтау керек;
2) бөлінгішті де сонша есе арттыру керек;
3) жаңа бөлінгішті жаңа бөлгішке бөлу керек.
Мысалы, 31,26 санын 0,015-ке бөлейік. Онда ереже бойынша 0,015-тегі
үтірді алып тастап, осы санның неше еce артқанын анықтаймыз:
15 = 0,015 · 1000.
Демек бөлгіш 1000 есе артқан. Бөлінді өзгермеу үшін бөлінгішті де 1000
есе арттыру қажет:
31,26 · 1000 = 31260.
Соңғы қадам – шыққан 31260 санын 15 натурал санына бөлеміз:
31260:15 = 2084.
31,26 : 0,015 амалының орындалуын басқаша жазуға болады:
31,26 : 0,015 = (31,26 · 1000) : (0,015 · 1000) = 31260 : 15 = 2084.

Сандық және әріпті өрнектер
§16. Әріпті өрнектер.
Әріпті өрнектердің мәндері

Белгісіз санды белгілеуге арналған әріптер арқылы жазылған өрнек әріпті
өрнек деп аталады. Әріптердің орнына қандай да бір сандық мәндерді қойып,
әріпті өрнектің тиісті мәндерін табамыз.
Егер әріптердің мәндері берілсе, өрнектегі бірдей әріптердің орнына
бірдей сан қойылады.
Мысалы,
(3а - 0,2) : (а - 5) + 2,2b өрнегінің мәнін табайық.
1) a = 5, b = 7;
2) а = 10, b = 0,1.
Шешуі.
1) (3 · 5 – 0,2) : (5 – 5) + 2,2 – 7.
Бұл өрнектің мәнін табу мүмкін емес, себебі санды нөлге бөлуге
болмайды.
2) (3 · 10 – 0,2) : (10 – 5) + 2,2 – 0,1 = 29,8 : 5 + 0,22 = 6,18.

§17. Көбейткіштері әріптен тұратын өрнектерді қысқартып жазу

Әріптер мен жақша алдындағы көбейту белгісін жазбау қабылданған. Ал
сандардың алдындағы көбейту белгісінің жазылуы міндетті.
Мысалы,
3 · a · с = 3ас; 2,5 · (b + 7,2) = 2,5 (b + 7,2).
Ал q · 3,1 өрнегіндегі көбейту таңбасын қалдыруға болмайды.
a · 5,7 + (b+7,2) · 3 өрнегі қысқартылып жазылмайды.
Көбейтіндіде бірнеше сандар немесе бірдей әріптер кездессе,
төмендегідей қысқартып жазуға болады:
1) сан көбейткіштерді өрнектің алдына қою және көбейту;
2) бірдей әріптерді тізіп жазып, оларды дәрежесімен алмастыру. Мысалы,
7ab · 1a · 3b = (7 · 1 · 3) · (a · a) · (b · b)=21a2b2.

Жай бөлшектер. Проценттер
§18. Жай бөлшектер.
Дұрыс және бұрыс бөлшектер

Жай бөлшек дегеніміз - түріндегі сандар, мұндағы т және п -
натурал сандар. т саны бөлшектің алымы, п бөлшектің бөлімі деп аталады.
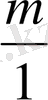Дербес жағдайда п = 1 бола алады, бұл жағдайда бөлшек түрінде болады,
бірақ бұны көбінесе жай ғана т деп жазады. Бұл әрбір натурал санды бөлімі 1
болатын жай бөлшек түрінде өрнектеуге болатынын білдіреді. Жай бөлшекті
мынадай мысал арқылы түсінуге болады:
Пирог тең төртке бөлінген. Олардың 1 бөлігі бір тәрелкеге, 3 бөлігі
екінші тәрелкеге салынған. Яғни бірінші тәрелкеге пирогтың төрттен бір
бөлігі, екінші тәрелкеге төрттен үш бөлігі салынған. Мұны былай жазып
көрсетеді: пирогтың 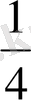бөлігі және 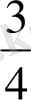бөлігі. 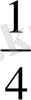және 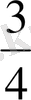сияқты
жазуларды жай бөлшектер деп атайды да, төрттен бір, төрттен үш деп
оқиды. Осы бөлшектердегі 1 және 3 сандары бөлшектің алымы, ал 4 саны бөлімі
деп аталады.
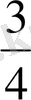бөлшегінің бөлімі бірлікті (яғни пирогты) неше тең бөлікке
бөлгенін көрсетеді, ал алымы (3 саны) сол бөліктің нешеуін алғанын
көрсетеді.
бөлшектерін сан осінде белгілеуде бірлік кесіндіні тең алты
бөлікке бөліп, осы бөліктің 5, 6 және 9-ынан тұратын жаңа кесіндіні
белгілеу қажет. Мұнда бөлшегі бірдің сол жағында жатады (бірден кем),
ал бөлшегі бірмен беттеседі (бірге тең), бөлшегі бірдің оң
жағында жатады (бірден артық).
Жай бөлшектерді дұрыс және бұрыс бөлшектер деп те ажыратады. Бөлімі
алымынан артық болатын бөлшек дұрыс, ал кіші не тең болатын бөлшек бұрыс
бөлшек деп аталады.
бөлшегі – дұрыс (6 5) бөлшек. Кез келген дұрыс бөлшек нөл мен
бірдің арасында жататындықтан бірден кем.
бөлшегі – бұрыс бөлшек (6 = 6).
бөлшегі – бұрыс (6 9) бөлшек. Кез келген бұрыс бөлшек бірдің оң
жағында орналасатындықтан, әрқашанда бірден артық немесе тең.

§19. Бөлімдері бірдей бөлшектерді салыстыру, қосу және азайту. Натурал
санды бөлімі кез келген сан болатын бөлшектүрінде жазу

Бөлімдері бірдей екі бөлшектің қайсысының алымы аз болса, сол бөлшек
келесі бөлшектен аз болады және қайсысының алымы үлкен болса, сол бөлшек
келесі бөлшектен үлкен болады. Кез келген бұрыс бөлшек кез келген дұрыс
бөлшектен артық болады.
өйткені бөлшектерінің бөлімдері бірдей, ал 13 7.
және бөлшектерін жоғарыда айтылған ереже бойынша
салыстыруға болмайды, олардың бөлімдері әр түрлі.
себебі бөлшегі – бұрыс бөлшек, ал бөлшегі – дұрыс
бөлшек.
Бөлімдері бірдей бөлшектерді қосқанда, бірінші бөлшектің алымына екінші
бөлшектің алымын қосып, бөлімін өзгеріссіз қалдырады:

Бөлімдері бірдей бөлшектерді азайтқанда, бірінші бөлшектің алымынан
екінші бөлшектің алымын азайтып, бөлімін өзгеріссіз қалдырады:

Мысалы,

қосындысын тапқанда, бөлімдері бірдей бөлшектерді қосу ережесін
пайдалануға болмайды.
Кез келген а натурал санын бөлімі кез келген натурал п болатын бөлшек
түрінде келесі формула арқылы жазуға болады:

Мысалы,

Бөлшек және натурал сандарды өзара салыстыру, қосу және азайту үшін
алдымен натурал санды берілген бөлшекпен бөлімі бірдей бөлшек түрінде жазу
қажет. Мысалы, 2 және сандарын салыстырайық, қосайық және азайтайық:
болғандықтан,

§20. Аралас сандар

Натурал сан мен дұрыс бөлшектің қосындысын + таңбасын қолданбай жазу
қабылданған. Мұндай қосындыны аралас сан деп атайды.
Натурал сан аралас санның бүтін бөлігі, ал бөлшек аралас санның бөлшек
бөлігі деп аталады. Мысалы,

мұндағы 31 – аралас санның бүтін бөлігі, ал - бөлшек бөлігі.
Аралас санды бұрыс бөлшек түрінде де жазуға болады:

Ал бұрыс бөлшекті аралас сан түрінде де жазуға болады.
Бұрыс бөлшекті аралас сан түрінде жазу бүтін бөлікті бөліп шығару деп
аталады.
Бүтін бөлікті бөліп шығару үшін, бөлшектің алымын бөліміне бөліп,
аралас санды жазу керек, онда:
1) бүтін бөлік - бөлгендегі бөлінді;
2) бөлшек бөлігінің алымы - бөлгеңдегі қалдық;
3) бөлшек бөлігінің бөлімі - берілген бұрыс бөлшектің бөлімі.
Бұрыс бөлшектің алымын бөліміне бөлгендегі қалдық нөлге тең болса, онда
бұрыс бөлшек белгенде шыққан натурал санға тең.
Мысалы, бөлшегінің бүгін бөлігін бөліп шығарайық:
131 : 8 = 16 (қалдық 3-ке тең);
бөлшегінің бүтін бөлігін бөліп шығарайық:
13104 :13 = 1008.
Демек бөлшегі 1008 натурал санына тең.

§21. Бөлімдері бірдей аралас сандарды қосу және азайту

Аралас сандардың қосындысын табу үшін әрқайсысының жеке-жеке бүтін және
бөлшек бөліктерін қосу қажет.
Егер бөлшек бөліктерін қосқанда бұрыс бөлшек шығатын болса, онда бұл
бөлшектің бүтін бөлігін тауып, осының алдында табылған бүтін бөлікке қосу
керек. Мысалы:

Аралас сандардың айырымын табу үшін бүтін бөліктерінің айырымын, бөлшек
беліктерінің айырымын жеке-жеке табу керек.
Егер азайғыш бөлшектің алымы азайтқыш бөлшектің алымынан аз болса, онда
оған алдын ала бүтін бөлігінен 1-ді шегеріп, осы бөлшек бөлімге қосу керек.
Мысалы:

Немесе берілген аралас сандардың қосындысын, айырымын табу үшін сол
сандардын, әрбіреуін бұрыс бөлшекке келтіріп, содан кейін қосуды, азайтуды
орындаймыз. Мысалы:

§22. Бөлшек арқылы шешілетін есептердің үш түрі

1) Берілген санның көрсетілген бір бөлігін табу.
2) Қандай да бір бөлігі белгілі санды табу.
3) Бір сан екінші бір санның қандай бөлігін құрайтындығын табу.
Бөлшекке берілген есептерді келесі түрде шешуге болады.
1) Суреті салынады. Бұл суретте:
а) түзуде ұзындығы белгілі немесе белгісіз шамаға тең кез келген
бүтін кесіндіні белгілейміз;
б) осы кесіндінің белгілі немесе белгісіз бөлігін жуықтап белгілейміз;
в) кесіндіге және оның бөлігіне олармен анықталатын белгілі немесе
белгісіз шамалар белгіленеді.
2) Бүтіннің бір бөлігі неге тең екендігі анықталады.
3) Ізделетін шама табылып, жауабы жазылады.

1-мысал

72 метрдің бөлігін табайық.
Шешудің бірінші қадамы - есептің суретін салу. Суретті кез келген бір
кесінді салудан бастаймыз. Кесіндінің ұзындығына 72 м сәйкес келеді деп
ұйғарамыз. Осы кесіндінің бөлігін табу керек. Есеп суретін салудың
келесі қадамында 72 санының бөлігін құрайтын санды жуықтап саламыз.
Бұл кесіндінің ұзындығы белгісіз, суретте т арқылы белгіленген.

Келесі қадамда бүтіннің бір бөлігі неге тең екенін анықтаймыз.
Тең 8 бөлікке бөлінген бірлік кесіндінің әрбір бөлігінің ұзындығы
72 : 8 = 9.
Басқаша айтқанда, 72-нің бөлігі дегеніміз - 72 : 8 = 9.
Шешудің соңғы қадамында ізделетін шаманы тауып, жауабын жазамыз.
Сонымен, 72-нің бөлігі дегеніміз - (72 : 8) · 3 = 27.
Жауабы. 72 м-дің бөлігі 27 м-ге тең.

2-мысал
бөлігі 77-ге тең болатын санды табайық.
Есепті шешудің бірінші қадамы – есеп суретін салу. Сурет салуды кез
келген кесінді салудан бастаймыз. Бұл кесіндінің ұзындығы белгісіз к санына
тең деп ұйғарамыз.
Есеп шарты бойынша к санының бөлігі 77-ге тең.
Оны кескіндеу үшін к кесіндісін тең 7 бөлікке бөліп, бір бөлігін 11 рет
салу керек.

Есепті шешудің келесі қадамында бүтіннің бір бөлігі неге тең екенін
табу керек. Ол үшін бөліктің 77-ге тең екенін пайдаланамыз. Кесінді
бөлінген 11 бөліктің әрқайсысының ұзындығы 77 : 11 = 7. к кесіндісі тең 7
бөлікке бөлінген, әр бөлігі 77 : 11 = 7. Есептің соңғы қадамы – белгісіз
шаманы тауып, есептің жауабын жазу.
к = (77 : 11) · 7 = 49.
Жауабы. Белгісіз сан 49-ға тең.

3-мысал

23 м мата сатып алынды. Осы матаның 20 метрі жұмсалған болса, матаның
қанша бөлігі жұмсалған.
Сатып алынған матаның ұзындығын сипаттайтын кесіндіні сызайық.
Жұмсалған матаның ұзындығын суретте белгісіз санмен белгілейік.

Егер 23 м-ді ойша жекелеген метрлерге бөлсек, онда әрбір бөлік барлық
матаның бөлігін кұрайды, 23 м берілген матаның бөлігін, ал 20 м
берілгёр матаның бөлігін кұрайды.
Жауабы. 20 м - 23 м матаның бөлігі.

§23. Проценттер

Кез келген екі сан үшін біріншісі екіншісінің қанша бөлігін кұрайтынын
анықгауға болады. Мысалы, 168 саны 200-дің бөлігін құрайды.
Бір санның екінші санды құрайтын бөлігін көбінесе жүздік үлеспен немесе
процентпен өрнектейді. Процент сөзінің орнына % белгісін пайдаланады.
Процент деп қандай да бір санның жүзден бір бөлігін айтады.
Ондық бөлшектердің ішіндегі 0,01 бөлшегі 1% болып табылады. Дәл солай
2% = 0,02; 45% = 0,45 және т.с.с. Сонымен, бір санның екінші санды құрайтын
бөлігін b деп белгілесек, осы бөліктің процентпен өрнектелуін f деп алсақ,
онда f = b : 0,01.
Мысалы, 15саны 12-нің неше процентін құрайтынын анықтайық. Ол үшін
алдымен 15 саны 12-нің қанша бөлігін құрайтынын анықтаймыз.

15 саны 12-нің бөлігін кұрайды. b = f : 0,01 формуласындағы b-ның
орнына 1,25 санын қойсақ, b = 1,25 : 0,01 = 125.
Сонымен, 15 саны 12-нің 125%-ін құрайды.
Егер, мысалы, а саны т санының 28%-ін құрайтын болса, онда а саны т
санының қанша бөлігін құрайтынын табуға болады.
f = b : 0,01 формуласындағы f -тың орнына 28-ді қойсақ:
28 = 6 : 0,01.
Теңдіктің екі жағын 0,01 -ге көбейтсек:

Берілген санның қандай да бір процентін табу немесе оның қандай да бір
сандағы проценті белгілі болса, онда мұндай есептер бөлшекке берілген
есептер сияқты шешіледі.

1-мысал.

0,5 санының 23%-ін табайық.
23% дегеніміз болғандықтан, қарастырып отырған есебіміздің
бөлшекке берілген есептерден ешқандай айырмашылығы жоқ:

1% немесе -ге 0,5 : 100 = 0,005 сәйкес келеді.
23% немесе -ке (0,5 : 100) · 23 = 0,115 сәйкес келеді.
Жауабы. 0,5 санының 23%-і 0,115-ке тең.

2-мысал

45%-і 5,4-ке тең болатын санды табайық.

1%-ке 5,4 : 45 = 0,12 саны сәйкес келеді. Ал 100%-ке 100 · (5,4 : 45) =
12 саны сәйкес келеді.
Жауабы. Белгісіз сан 12-ге тең.

§24. Бөлшектердің теңдігі. Бөлшектің негізгі қасиеті. Бөлшектерді
қысқарту

Егер ad = bс болса, мен бөлшектері тең деп есептеледі.
Мысалы, пен бөлшектерітең, өйткені 3 · 15 = 5 · 9.
Бөлшектердің теңдігі анықтамасынан мен бөлшектерінің
теңдігі шығады, өйткені а(bп) = b(ап). Бұл жерде біз натурал сандарды
көбейтудің терімділік және орын ауыстырымдылық қасиеттерін пайдаландық.
Демек

яғни егер берілген бөлшектің алымы мен бөлімін бір ғана натурал санға
көбейтсек немесе бөлсек, онда берілген бөлшекке тең бөлшек алынады. Бұл
қасиет бөлшектің негізгі қасиеті деп аталады. Мысалы,
өйткені
өйткені
Бөлшектің негізгі қасиетін пайдаланып, кейде берілген бөлшекті өзіне
тең, бірақ алымы мен бөлімі берілген бөліпектің сәйкес алымы мен бөлімінен
кіші бөлшекпен ауыстыруға болады. Мұндай ауыстыруды бөлшекті қысқарту деп
атайды.
бөлшегін бөлшегімен ауыстыру үшін теңдігін пайдалану
бөлшекті қысқарту болып табылады. Мысалы,
(алымы мен бөлімін бір ғана 3 санына бөлдік).
Алынған бөлшекті алымы мен бөлімін 5-ке бөліп, тағы да қысқартуға
болады:

Жалпы жағдайда, егер бөлшектің алымы мен бөлімі өзара жай болмаса,
бөлшекті қысқартуға болады; егерде алым мен бөлім өзара жай болса, онда
бөлшек қысқармайтын бөлшек деп аталады.
Мысалы, - қысқармайтын бөлшек.
Бөлшекті қысқартудың негізгі мақсаты - осы бөлшекті өзіне тең
кысқармайтын бөлшекпен ауыстыру.

§25. Ең үлкен ортақ бөлгіш. Ең кіші ортақ еселік

Берілген екі санның екеуі де бөлінетін ортақ бөлгіштерінің ішіндегі ең
үлкенін осы екі санның ең үлкен ортақ бөлгіші деп атайды. а және b
сандарының ең үлкен ортақ бөлгіші ЕҮОБ (а; b) түрінде бөлгіленеді.
ЕҮОБ (a; b) табу үшін:
1) а және b сандарын жай көбейткіштерге жіктеп, екі санға да қатысып
тұрған жай сандарды белгілеп қою керек;
2) белгіленген жай көбейткіштердің көбейтіндісін табу керек.
Мысалы, ЕҮОБ (1572; 2718) былай табылады:

Кейде қарастырып отырған сандарда бірдей жай көбейткіштердің болмауы да
мүмкін.
Мысалы, 12 = 2 · 2 · 3; 55 = 5 · 11.
Бұл – 55 және 12 сандары тек қана 1-ге бөлінеді деген сөз.
Сондықтан ЕҮОБ (55; 12) = 1.
Ең үлкен ортақ бөлгіші бірге тең сандар өзара жай сандар деп аталады.
Немесе, егер ЕҮОБ (а; b) = 1 болатындай сандар болса, онда а мен b
өзара жай сандар деп аталады. Мысалы, 72 мен 35 сандары (олардың әрқайсысы
кұрама сан болса да) - өзара жай сандар.
Бірнеше санның ең үлкен ортақ бөлгішін табу үшін бұл сандарды жай
көбейткіштерге жіктеу керек те, ең кіші дәрежелерімен алынған ортақ жай
көбейткіштердің көбейтіндісін табу керек.
Мысалы, ЕҮОБ (48; 60; 72) табу керек.
Шешуі:

48 санының жіктелуіне де, 60 санының жіктелуіне де, 72 санының
жіктелуіне де енетін жай көбейткіштер (ең кіші дәрежелі) алынған.
Жауабы: ЕҮОБ (48; 60; 72) = 22 · 3 = 12.
b натурал санына бөлінетін а натурал саны b-ға еселі деп аталады.
Мысалы, 14 саны 7-ге бөлінетіндіктен, 7-ге еселі, 15 саны 7-ге еселі емес,
себебі 7-ге бөлінбейді.
Берілген екі санға да еселі болатын ортақ еселіктерінің ішіндегі ең
кішісін осы екі санның ең кіші ортақ еселігі деп атайды.
а және b сандарының ең кіші ортақ еселігі ЕКОЕ (а; b) түрінде
белгіленеді.
ЕКОЕ (а; b) табу үшін:
1) а және b сандарын жай көбейткіштерге жіктеп, екі санға да қатысып
тұрған жай сандарды белгілеп қою керек;
2) бір санға қатысып тұрған барлық жай көбейткіштерге екінші сандағы
белгіленбеген жай көбейткіштерді қосып көбейту керек.
Мысалы, ЕКОЕ (36; 60) табайық:

ЕКОЕ (12; 25) табайық:

12 және 15 сандарында ортақ жай көбейткіштер жоқ болғандықтан, ЕКОЕ
ретінде осы екі санның барлық жай көбейткіштерінің көбейтіндісін аламыз:
ЕКОЕ (12; 25) = 2 · 2 · 3 · 5 · 5 = 300.
Бірнеше санның ең кіші еселігін табу үшін бұл сандарды жай
көбейткіштерге жіктеу керек те, барлық алынған жай көбейткіштердің (оларды
ең үлкен дәрежесімен алып) көбейтіндісін табу керек.
Мысалы, ЕКОЕ (3780; 7056) табу керек.
Шешуі:

Сонда сандардың кемінде біреуінің жіктелуіне енетін барлық жай
көбейткіштер алынған. Сонымен
ЕКОЕ (3780; 7056) = 24 · 33 · 5 · 72 = 105840.
Кез келген а және b натурал сандар үшін
ЕҮОБ (а; b) · ЕКОЕ (a;b) = a · b
теңдігі орынды. Егер а және b сандары өзара жай, яғни ЕҮОБ (а; b) = 1
болса, онда ЕКОЕ (a; b) = a · b. Бұл өзара жай екі санның ең кіші ортақ
еселігі осы сандардың көбейтіндісіне тең болатынын білдіреді.

§26. Бөлшектерді ортақ бөлімге келтіру

Бөлімдері әр түрлі болатын бөлшектерге бөлшектің негізгі қасиетін
пайдаланып, өздеріне тең басқа бөлшектермен ауыстыруға болады, сонда
алынған бөлшектердің бөлімдері тең болуы керек. Мұндай түрлендіру
бөлшектерді ортаң бөлімге келтіру деп аталады.
Бөлшектердің ортақ бөлімі - бөлшектердің бөлімдеріне еселі сан, ал
олардың ең кішісін ең кіші ортақ бөлім деп атайды.
Бөлшектерді ең кіші ортақ бөлімге келтіру үшін:
1) бөлшектер бөлімдерінің ЕКОЕ-сін табу;
2) ЕКОЕ-ні әрбір бөлімге бөліп, қосымша көбейткіштерді есептеу;
3) әрбір бөлшектің алымы мен бөлімін сәйкес қосымша көбейткішке көбейту
керек.
Мысалы,
және бөлшектерін ең кіші ортақ бөлімге келтірейік.
Шешудің бірінші қадамы 1485 және 825 сандарының ЕКОЕ-сін табамыз.

Ең кіші ортақ бөлгішті табу әдісінен көріп отырғанымыздай, бірінші
бөлшектің алымы мен бөлімін 5-ке, ал екінші бөлпіектің алымы мен бөлімін 9-
ға көбейтеміз.
Қосымша көбейткіштер 5 және 9 сандарын ЕКОЕ-ні сәйкес әрбір бөлшектің
бөліміне бөліп табуға да болады:

Сонымен бөлшектерді ортақ бөлімге көптеген тәсілдермен келтіруге
болады, бірақ, әдетте, бөлшектерді ең кіші ортақ бөлімге келтіруге
тырысады, ол берілген бөлшектер бөлімдерінің ең кіші ортақ еселігіне тең.

§27. Бөлшектерді және аралас сандарды салыстыру, қосу және азайту

Кез келген бөлшектерді алдын ала ортақ бөлімге келтіру арқылы
салыстыруға, қосуға және азайтуға болады.
Қосуды орындағаннан кейін шыққан бөлшек бұрыс болса, онда бүтін бөлігін
бөліп шығару қажет; қосу және азайту амалдарын орындағаннан кейін шыққан
бөлшекті қысқартуға бола ма, оны тексеру қажет.

1-мысал

және ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.