Эмпирикалық қисықтардың гармоникалық талдауы: Фурье мен Бессель формулалары және іс-тәжірибелік әдістер


Тарау І Гормоникалық талдаудың гормоникалық талдау іс-тәжірибелік әдістері
§ 1 Эмперикалық қисықтардың гармоникалық талдауы
Жоғарыда көргеніміздей, егер Дирихле шарттарын қанағаттандаратын
 периодты функциясы берілсе, онда бұл функцияның кез-келген ретті гормоникаларын жұп-жұптан анықтайтын Фурье коэффиценттері
периодты функциясы берілсе, онда бұл функцияның кез-келген ретті гормоникаларын жұп-жұптан анықтайтын Фурье коэффиценттері
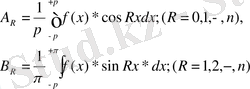
формулаларымен табылады.
Іс жүзінде, алайда, көп жағдайда функция аналитикалық өрнегі белгісіз қандай да бір қисық түрінде графиктін түрде берілді. Бұндай эмперикалық қисықтар әдетте қандай да бір айнымалы шаманың өзге бір шаманың өзгеруіне байланысты өзгерісін графиктік түрде тіркейтін құрылғының көмегімен алынады. Осындай құрылғыларға, мысалы, осциллографтар, торсиографтар және т. б. жатады.
Сонымен қатар, функция аргументін белгілі бір мәндеріне сәйкес қандай да бір саны шектеулі өзінің дербес мәндерімен ғана жиі беріледі. (функцияның кестелі тәсілмен берілуі) . Функцияның бұл дербес мәндері қарастырылып отырған айнымалы шаманы бақылау және өлшеу нәтижесі болып табылады. Мысалы, берілген жерде тәуліктің белгілі бір аралықтарына ауа температурасын бақылау нәтижесінде сандық мәндер қатары пайда болады, оларды функцияның дербес мәндері ретінде қарастыруға болады, яғни осы жағдайдағы жергілікті ауаның температурасы.
Егер
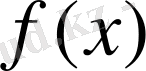 функциясы аналитикалық өрнегі белгісіз эмпирикалық қисық түрінде берілген жағдайда (*) формулалардың тікелей қолданылуы мүмкін болмайтыны анық. Егер де функция тек өзінің дербес мәндерімен берілсе, онда жоғарыдағы талқылаулар мен тұжырымдар тіпті қолданылмайды.
функциясы аналитикалық өрнегі белгісіз эмпирикалық қисық түрінде берілген жағдайда (*) формулалардың тікелей қолданылуы мүмкін болмайтыны анық. Егер де функция тек өзінің дербес мәндерімен берілсе, онда жоғарыдағы талқылаулар мен тұжырымдар тіпті қолданылмайды.
Бұл жағдайларда функцияның гармоникаларға бөлінуі басқаша түрде қойылуы мүмкін.
Қандай да периодты эмпирикалық қисық бар болсын периоды 2
 -ге тең деп алайық. Бұл периодты р тең бөліктеріне бөлеміз. Абциссаның бөліну нүктелері
-ге тең деп алайық. Бұл периодты р тең бөліктеріне бөлеміз. Абциссаның бөліну нүктелері
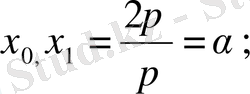
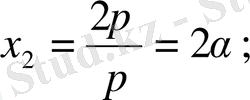 . . .
. . .
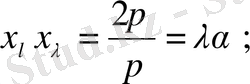
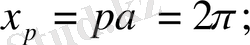 ал сәйкес ординаталар
ал сәйкес ординаталар
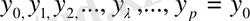 болсын нометриялық полиналды алайық.
болсын нометриялық полиналды алайық.
Онда келесі есепті қоюға болады
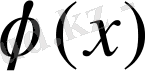 полиналы бөліну нүктелерінде осы нүктелердегі ордината мәндеріне жақындайтындай
полиналы бөліну нүктелерінде осы нүктелердегі ордината мәндеріне жақындайтындай
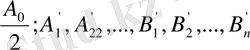 коэффиценттерінің мәндерін анықтау керек; басқаша айтқанда, полиномды бөліну нүктелерінде берілген ординаталардан ауытқу квадраттарының қосындысы осы нүктелерде минимальды болатындай коэффиценттің мәндерін анықтау керек, яғни
коэффиценттерінің мәндерін анықтау керек; басқаша айтқанда, полиномды бөліну нүктелерінде берілген ординаталардан ауытқу квадраттарының қосындысы осы нүктелерде минимальды болатындай коэффиценттің мәндерін анықтау керек, яғни
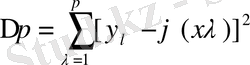 қосындысы ең аз болуы керек.
қосындысы ең аз болуы керек.
Дәл осы есепті өзгеріссіз функция тек өзінің дербес мәндерімен
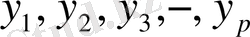 белгілі жағдай үшін де қоюға болады.
белгілі жағдай үшін де қоюға болады.
Жоғарыдағы аталған шарттарды қанағаттандыратын
 полиномының коэффиценттерін анықтау процессі эмпирикалық қисықтың немесе функцияның дербес мәндер қатарының гормоникалық талдауы.
полиномының коэффиценттерін анықтау процессі эмпирикалық қисықтың немесе функцияның дербес мәндер қатарының гормоникалық талдауы.
§ 2 Бессель формулалары
Жоғарыдағы қойылған есепті шығару берілген теориялық сәйкес
 --дан
--дан
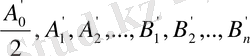 бойынша дербес туынды алып, оларды нөлге теңестіру керек. Нәтижесінде
бойынша дербес туынды алып, оларды нөлге теңестіру керек. Нәтижесінде
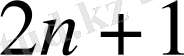 белгісізі бар, дәл саны келесі теңдеулер алынады. Нормаль теңдеулер деп аталатын
белгісізі бар, дәл саны келесі теңдеулер алынады. Нормаль теңдеулер деп аталатын
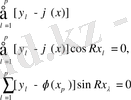
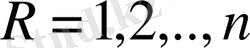 (1. 2)
(1. 2)
Бұл теңдеулер жүйесін шешу алдын-ала келесі қажетті формулаларды шығарып алайық.
Ең бірінші
 және
және
 қосындыларының мәндерін анықтаймыз. Бұл үшін екінші қосындыны і-ға көбейтіп, бірінші қосындыға қосамыз; сонда
қосындыларының мәндерін анықтаймыз. Бұл үшін екінші қосындыны і-ға көбейтіп, бірінші қосындыға қосамыз; сонда
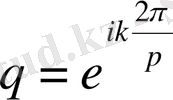 деп белгілеп, біз келесіні аламыз:
деп белгілеп, біз келесіні аламыз:

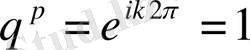 екенін ескертеміз. Екіншіден,
екенін ескертеміз. Екіншіден,
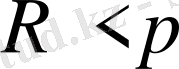 болғандықтан
болғандықтан
 р-ға еселі емес Сондықтан
р-ға еселі емес Сондықтан
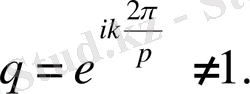 Ендеше,
Ендеше,
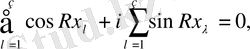 (1. 4)
(1. 4)
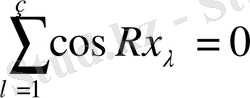
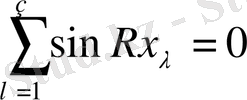 (1. 5)
(1. 5)
Әрі қарай келесі қосындының мәндерін анықтаймыз.
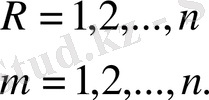
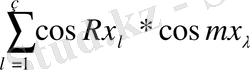
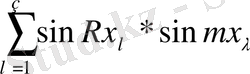
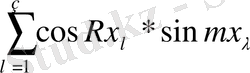
Тікелей келесі аламыз.
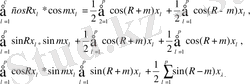
(1. 5) негізінде
 болғаннан басқа жағдайларда соңғы теңсіздіктердің оң жағындағы барлық қосындылар 0-ге тең. Сондықтан
болғаннан басқа жағдайларда соңғы теңсіздіктердің оң жағындағы барлық қосындылар 0-ге тең. Сондықтан
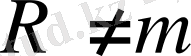
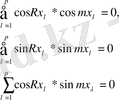
формуласын аламыз
 болғанда келесіні аламыз:
болғанда келесіні аламыз:
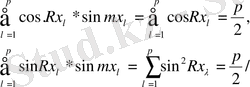
(1. 7)
(1. 8)
Жоғарыдағы аталған теңдеулер жүйесінің шешіміне келейік. (1. 4), (1. 5), (1. 6), (1. 7) формулаларын ескере отырып, (1. 1) теңдігінен келесіні аламыз.
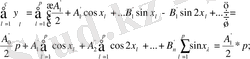
(1. 2) теңдеулерінен келесіні аламыз.
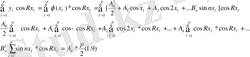
- теңдіктерінен аналогиялы түрде келесіге ие боламыз.
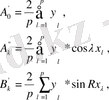
 (1. 11)
(1. 11)
Дербес жағдай.
Дербес жағдайда,
 тригонометриялық полиномының мүшелерр саны қисықтың эквидистантты ординаталар санына немесе функция берілген эквидистантты мәндер санына тең етіп алынуы мүмкін. Бұл жағдайда полиномның бөліну нүктелерінде функцияның сәйкес ординаталарынан ауытқуы нөлге те болатындай, полином коэффиценттерінің мәндерін анықтауға болады. Графиктік мағынадағы бұл
тригонометриялық полиномының мүшелерр саны қисықтың эквидистантты ординаталар санына немесе функция берілген эквидистантты мәндер санына тең етіп алынуы мүмкін. Бұл жағдайда полиномның бөліну нүктелерінде функцияның сәйкес ординаталарынан ауытқуы нөлге те болатындай, полином коэффиценттерінің мәндерін анықтауға болады. Графиктік мағынадағы бұл
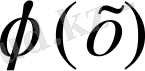 полиномын бейнелейтін қисық, өзінің таңдалған немесе берілген нүктелері арқылы өтетіндей коэффициенттердің мәндерін табуға болатынын білдіреді.
полиномын бейнелейтін қисық, өзінің таңдалған немесе берілген нүктелері арқылы өтетіндей коэффициенттердің мәндерін табуға болатынын білдіреді.
Біз мұнда екі жағдайды ерекшелейміз.
Егер таңдап алынған немесе бар ординаталар саны Р тақ болса
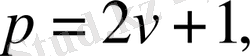 онда полиносның барлық 2v+1 коэффиценттері (1. 11) формула бойынша анықталады.
онда полиносның барлық 2v+1 коэффиценттері (1. 11) формула бойынша анықталады.
Егер таңдап алынған немесе бар ординаталар саны р жұп болса, яғни
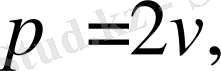 онда (1. 2) формуладан мынаны аламыз.
онда (1. 2) формуладан мынаны аламыз.
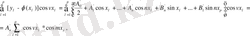
мұндағы,
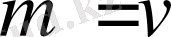 болғанда екінші қосынды р-ға тең, ал біріншісі мынаны береді:
болғанда екінші қосынды р-ға тең, ал біріншісі мынаны береді:
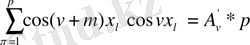 ендеше
ендеше
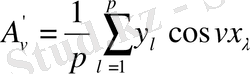 (1. 12)
(1. 12)
Сонымен қатар,
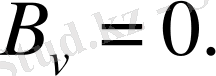
Бұл жағдайда, ендеше,
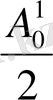 тұрақты мүшесі, ал кейін
тұрақты мүшесі, ал кейін
 конустық коэфиценттері және
конустық коэфиценттері және
 синустық коэффиценттері анықталуы мүмкін.
синустық коэффиценттері анықталуы мүмкін.
Сондықтан қарастырылып отырған жағдайда Бессель формулалары келесі түрге ие болады.
 (1. 13)
(1. 13)
Бұл жағдайда
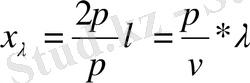 болғандықтан, (1. 13) формулаларын келесі түрде жазуға болады:
болғандықтан, (1. 13) формулаларын келесі түрде жазуға болады:
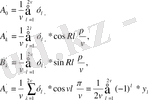 (1. 14)
(1. 14)
Жоғарыда аталған талаптарды қанағаттандыратын
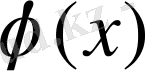 тригонометриялық полиномын анықтау процессі, яғни
тригонометриялық полиномын анықтау процессі, яғни
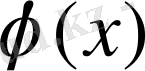 полиномының коэффиценттерін Бессель формулалары бойынша табу эмперикалық қисықтың немесе дербес мәндерімен берілген функцияның гармоникалық талдауы деп аталады. Жоғарыда айтқанымыздай
полиномының коэффиценттерін Бессель формулалары бойынша табу эмперикалық қисықтың немесе дербес мәндерімен берілген функцияның гармоникалық талдауы деп аталады. Жоғарыда айтқанымыздай
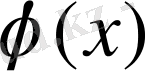 қосындысымен анықталатын синусонданы берілген эмперикалық қисықтың R-ретті гармоникасы д. а., Мұнда бұл гармоникалық жиілігі мен бастапқы фазасы бұрыңғы
қосындысымен анықталатын синусонданы берілген эмперикалық қисықтың R-ретті гармоникасы д. а., Мұнда бұл гармоникалық жиілігі мен бастапқы фазасы бұрыңғы
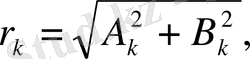
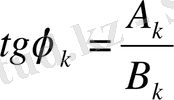
теңдеулерімен анықталады.
§ 3 Гармоникалық талдаудың іс-тәжірибелік әдістері туралы жалпы ескертулер
Периодты функцияларды құраушы гармоникаларға жіктеудің әртүрлі әдістері бар. Осы әдістердің теориялық негіздемесімен алғандағы барлығының жиынтығы іс-тәжірибелік гармникалық талдауды құрайды.
Гормоникалық талдаудың нақты тәсілдерін келесі топтарға бөлуге болады:
- арифметикалық немесе аналитикалық әдістер;
- графиктік әдістер;
- аралас әдістер;
- анализатор деп аталатын немесе аналогиялық құрылғылардың қолданылуы
- арнай кестелердің қолданылуы
Арифметикалық талдау дегеніміз талдау есептеу жолының көмегімен орындалатын діс, ал графиктік әдістер гармоникаларды сәйкес графиктік салулардың көмегімен алуға мүмкіндік береді.
Арифметикалық әдістер гармоникалардың саны едәуір көп болғанда өте көп есептеулер жүргізуді талап ететіндіктен, бұл есептеулерді жеңілдетуге арналған тәсілдер саны жеткілікті. Олардың қатарына келесілер жатады.
1) топтау схемалары;
2) шаблондар;
3) транспараттар;
4) Кестелер;
5) номограммалар және т. б.
Графиктік әдістердің ішінде техникада жиі кездесетін қисықтардың гормоникаларын анықтауға мүмкіндік беретін топ бар. Бұл ең бірінші абцисса өсіне қатысты жылжытылған симметриялы қисықтар. Бұл жағдайда, алдыңғы парагратардан білетініміздей жұп ретті гармоникалар жоқ. Бұндай алдына дербес мақсаттар қоятын әдістерге, мысалы Мейрер, Шрутк, Пихельмайер және т. б. әдістер жатады.
Іс-тәжірибелік гармоникалық талдаудың әдістері Фуры коэффиценттерін анықтау мақсатында пайдаланылады. Соңғысын тауып, одан кейін гармониклардың жиілігі мен бастапқы фазаларын анықтайды. Бұндай әдістерге, мысалы, Роте мен Мейскер әдістері жатады; дәл осы мақсат Шарт анализаторын қолдану арқылы орындалады.
Барлық әдістер кез-келген санды гармоникалар табуға болатынын теориялық жағынан растайды. Алайда, гармоникалар санының артуымен не есептеулер қиындығы, не талдау жүргізетін техникалық құрылғылар конструкцясының күрделілігі арта түседі, ал бұл саны көп гармоникаларды анықтаудың іс-тәжірибелік мүмкіндігіне шек қояды. әдетте әдістер 11, 17, 23 гармоникаларды анықтауға мүмкіндік береді. Тек Герицидің едеуір жақсартылған механикалық анализаторы 50-ретті қоса алғандағыға дейінгі гармоникаларды алуға мүмкіндік береді. Алайда, қазіргі заманда осындай жоғары ретті гармоникаларды алудың іс-тәжірибелік қажеттігі тірті жоқтың қасы екенін ескерту қажет.
Тарау ІІ Арифметикалық әдістер және топтау схемалары
§ 3 Китнер иен Перридің арифметикалық тәсілдері
Эмперикалық қисықтың ординаталарын немесе бақыланушы функцияның мәндерін гармоникалық талдауда арифметикалық әдістерді қолданғанда
 жұп санын алу қолайлырақ. Бұл жағдайда, (1. 14) формулаларынан байқайтынымыздай функцияның мәндері көбейтілетін синус пен косинус аргументтері үш көбейткіштен тұрады, анығырақ гармониканың ретін анықтайтын сандар, көбейтілетін ординаталардың индексі және
жұп санын алу қолайлырақ. Бұл жағдайда, (1. 14) формулаларынан байқайтынымыздай функцияның мәндері көбейтілетін синус пен косинус аргументтері үш көбейткіштен тұрады, анығырақ гармониканың ретін анықтайтын сандар, көбейтілетін ординаталардың индексі және
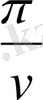 көбейткіші. Мысалыға,
көбейткіші. Мысалыға,
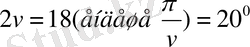 болғанда кестеде келтірілген бұрыштар қатарын аламыз.
болғанда кестеде келтірілген бұрыштар қатарын аламыз.
Китнер тәсілі (1. 13) формулаларын тікелей қолданудан тұрады және қарапайымдырақ болып табылады. Оның мәні мынада: берілген тек қатарға барлық эквидистантт ординаталарды, жанындағы тік қатарға барлық эквидистантты ординаталарды, жанындағы тік қатарға - берілген
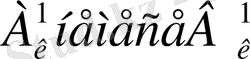 коэффиценттерін анықтау үшін қажет косинустардың немесе синустардың сәйкес барлық мәндерін тізіп жазып шығады; бұл сәйкес жұптас сандардың көбейтіндісін келесі екі қатарға жазады, балы көбейтіділерге арналған. Бұл екі тік қатардың қосындымсының алгебралық қосындысын
коэффиценттерін анықтау үшін қажет косинустардың немесе синустардың сәйкес барлық мәндерін тізіп жазып шығады; бұл сәйкес жұптас сандардың көбейтіндісін келесі екі қатарға жазады, балы көбейтіділерге арналған. Бұл екі тік қатардың қосындымсының алгебралық қосындысын
 ға бөліп,
ға бөліп,
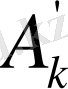 немесе
немесе
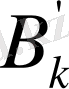 коэффиценттерін алады.
коэффиценттерін алады.
Алдынырақ Перри ұсынған тәсіл де негізінен осы тәсілге келтіріледі.
Кейінгі екі кестеде
 жағдайда үшін
жағдайда үшін
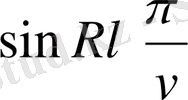 және
және
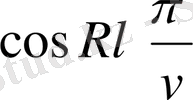 мәндері берілген, олар аталған және аналогиялы тәсілдерді пайдаланылады.
мәндері берілген, олар аталған және аналогиялы тәсілдерді пайдаланылады.
Р. А. Воронов Перри әдісінің графиктік интерполяциясын берген.
Аталған тәсілдер есептеулерге көп уақыт жұмсауды талар етеді. Келтірілген кесте мен формулалардан көрініп тұрғандай берілген бөліну саны 2v болғанда ординаталарды әр түрлі ретті гармоникалардың фурье коэффицентттерін анықтауда түрлі ретпен қайталанатын косинустар мен синустардың мәндерінің бір санына көбейтуге тур а келеді.
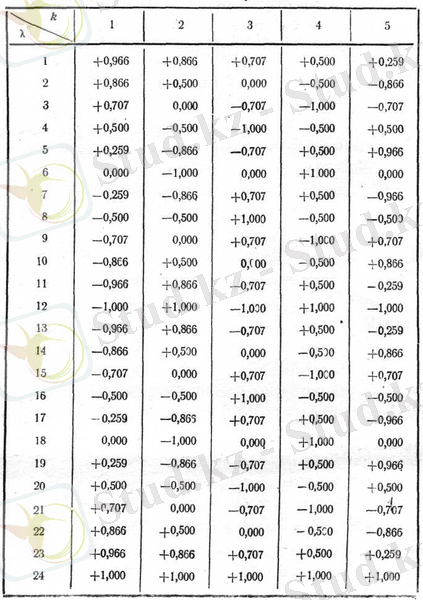
К-=1, 2, 3, 4, 5 және 1-ден 24-ке дейінгі
 үшін
үшін
 болғандағы
болғандағы
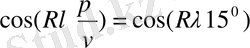 мәндерінің кестесі
мәндерінің кестесі
R=, 2, 3, 4, 5 және 1-ден 24-ке дейінгі
 үшін
үшін
 болғандағы
болғандағы
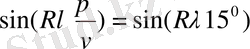 мәндерінің кестесі
мәндерінің кестесі
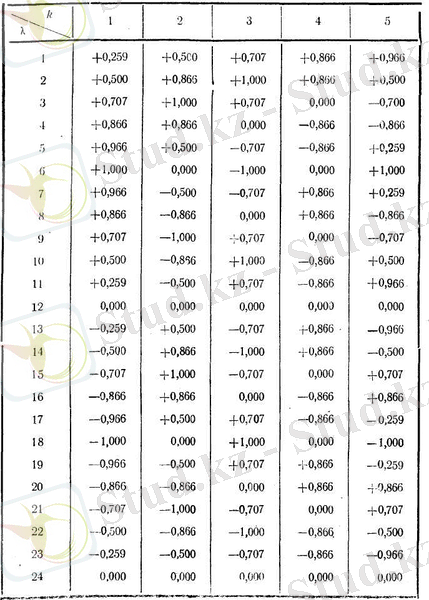
Бұдан көбейтінділер санын азайту үшін Фурьенің берілген екоэффиценттерін анықтауға косинус немесе синустың бір мәніне көбейтілетін барлық ординаталарды бірге топтауға мүмкін болатыны шығады.
Осыған байланысты бірқатар топтау схемалары ұсынылған, олардың негізінде кейбір ординаталар топтарын қосып, кейін ғана оларды белгілі бір сандарға көбейтуге болады. Бұл схемалардың негізгі т үрлері төменде сипатталған.
§ 4 Лар топтауы
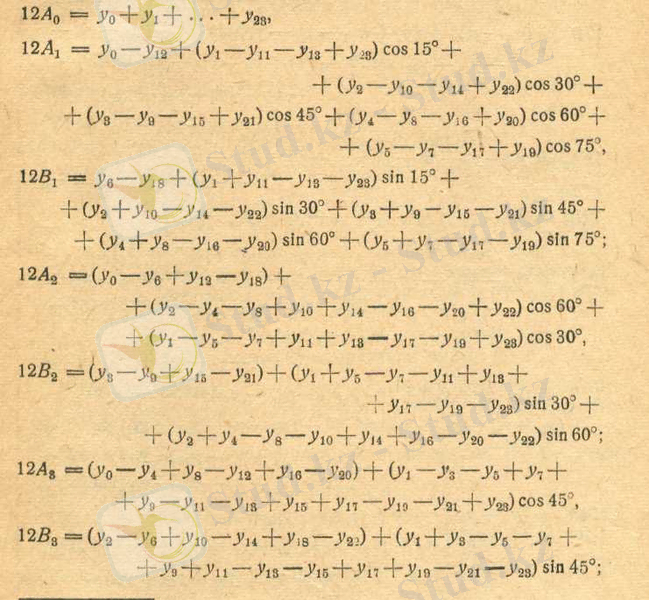
Лар дыбыс тербелістерін зерттей отырып, алғаш рет ординаталарды топтау әдісін қолданады. Қисықтың толқын ұзындығы 24 тең бөліктерге
 бөле отырып, (1. 14) Бессель формулаларынан келіп шығып, ол топтардың келесі схемасын қолданады:
бөле отырып, (1. 14) Бессель формулаларынан келіп шығып, ол топтардың келесі схемасын қолданады:



Қисықтың 11-ретті қоса алғандағыға дейінгі гармоникаларға жіктеуге Лар топтауы енгізетін қысқартуларға қарамастан, бәрібір іс-тәжірибеде оның пайдалануы өте көп есептеулер жүргізумен байланысты.
§ 5 Рунгенің топтау схемалары.
Рунгенің схемалары есептеулерді үлкен тездікпен орындау мағынасына едеіур жақсартылған болып табылады. Бұл схемалардың құрылуы келесіге негізделген.
Алдыңғыдай
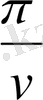 көбейткішін
көбейткішін
 арқылы белгілеп, (1. 14) формуласынан
арқылы белгілеп, (1. 14) формуласынан
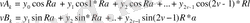
 формулаларын аламыз.
формулаларын аламыз.
Сонымен қатар,
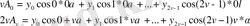
(2. 1) қатарынан у 0 енетін мүшесін есептемегенде басы мен соңынан бірдей қашықтықтағы екі мүшесін аламыз.
 және
және
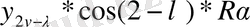
онда
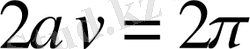 теңдігінің негізінде келесіге не боламыз.
теңдігінің негізінде келесіге не боламыз.

яғни, косинустық коэффиценттерді анықталғанда, у 0 енетін мүшесін есепке алмағанда қатардың басы мен санынан тең қашықтықтағы мүшелердің косинустық көбейткіштері өзара тең.
Дәл осылай у 0 енетін мүшесін есепке алмастан (2. 2) қатарының басы мен соңынан тең қашықтықтағы екі мүшесін алып келесіге ие боламыз.

яғни, синустық коэффиценттерді анықталғанда, у 0 енетін мүшесін есепке алмағанда қатардың басы мен соңымен тең қашықтытағы мүшелерінің алмағанда қатардың басы мен соңынна тең қашықтықтағы мүшелерінің синустық көбейткіштері абсюлют мәндері жағынан тең де, ал таңбалары қарама-қарсы.
Бұл жағдай абсолют мәндері тең көбейткіштерге ие ординаталарды топтауға мүмкіндік береді.
Дербес жағдай І
.
 болсын, онда абсолют мәндері бірдей көбейткіштерге келесі ординаталар жұбы ие болады.
болсын, онда абсолют мәндері бірдей көбейткіштерге келесі ординаталар жұбы ие болады.
у 1 мен у 11 ; у 2 мен у 10 ; у 3 пен у 9 ; у 4 пен у 5 ; пен у 7,
ал у 0 мен у 6 жалғыз қалады. Сондықтан ордината мәндерінің келесі екі қатарын жазамыз:
у 0, у 1, у 2, у 3, у 4, у 5, у 6, у 7, у 8, у 9, у 10, у 11.
Бұл қатарларда қосу және алу арқылы, келесі екі жаңа қатарды аламыз:
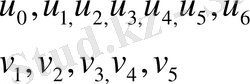
Мұнда
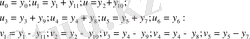
(2. 1) және (2. 2. ) теңдіктерінің негізінде
 болғанда
болғанда
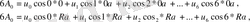
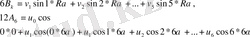
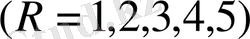 (2. 3)
(2. 3)
(2. 3) схема бойынша есептеулер жүргізудің орнына бірдей көбейткіштерге ие
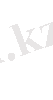
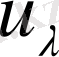 және
және
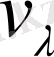 шамаларын әрі қарай тоатастыруға болатыны анық. Әрі қарайғы топтау анықтаушы гармоникалық R ретіне тәуелді.
шамаларын әрі қарай тоатастыруға болатыны анық. Әрі қарайғы топтау анықтаушы гармоникалық R ретіне тәуелді.
Жұп ретті гармоникалар үшін R=2R 1 екенін аламыз. (2. 3) қатарларының басы мен соңынан тең қашықтықтағы мүшелерін алып, келесіге ие боламыз.
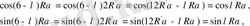
Тақ ретті гармоникалар үшін
 болады (2. 3) қатарларының басы мен санынан тең қашықтықтағы мүшелері үшін келесі қатынас орынды.
болады (2. 3) қатарларының басы мен санынан тең қашықтықтағы мүшелері үшін келесі қатынас орынды.
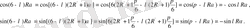 Сондықтан (2. 3) формулаларының екінші қатарынада u
0
мен u
6,
u
1
мен u
5,
. . . ординаталарының алдындағы көбейткіштер R-ның жұп мәндері үшін шамасы мен таңбалары бойынша тең болады, R-ның тақ мәндері үшін абсолют мәндері бойынша тең, бірақ таңбасы бойынша қарам-қарсы болады. (2. 3) формулаларының үшінші қатары үшін кері жағдай орындалады. Сондықтан u
0
мен v
6,
үшін келесі қатарларды жазамыз, ал кейін оларды қосып, аламыз.
Сондықтан (2. 3) формулаларының екінші қатарынада u
0
мен u
6,
u
1
мен u
5,
. . . ординаталарының алдындағы көбейткіштер R-ның жұп мәндері үшін шамасы мен таңбалары бойынша тең болады, R-ның тақ мәндері үшін абсолют мәндері бойынша тең, бірақ таңбасы бойынша қарам-қарсы болады. (2. 3) формулаларының үшінші қатары үшін кері жағдай орындалады. Сондықтан u
0
мен v
6,
үшін келесі қатарларды жазамыз, ал кейін оларды қосып, аламыз.
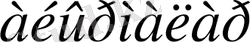

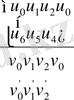

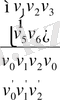
Сонымен келсені аламыз:
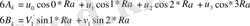
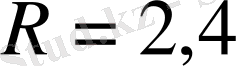 үшін
үшін
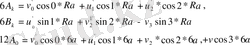
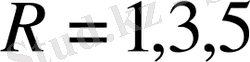 үшін (2. 4)
үшін (2. 4)
Қарстырылып отырған жағдайда
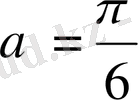 болғандықтан, бұнда кездесетін барлық синустар мен косинустар тек келесі мәндерге ие бола алады:
болғандықтан, бұнда кездесетін барлық синустар мен косинустар тек келесі мәндерге ие бола алады:
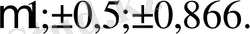
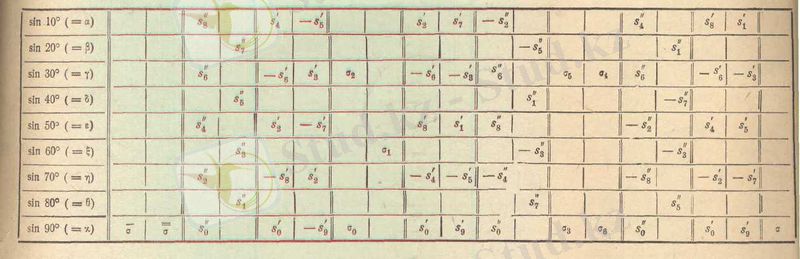
- теңдіктерін анықтайтын барлық рекеттер жиынтығын төмендегісі схемаға келтіруге болады.
Табылған
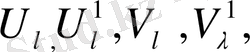 мәндерін келесі схемаға енгіземіз:
мәндерін келесі схемаға енгіземіз:
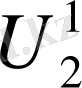
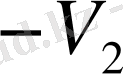
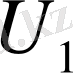
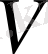
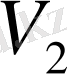
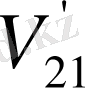
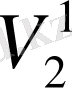
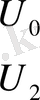
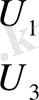
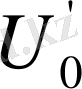

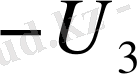

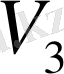
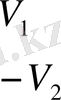
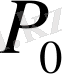
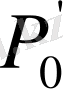
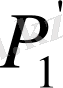
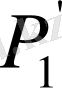
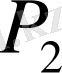
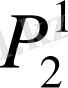
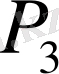

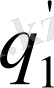
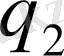
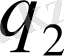
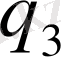

Бұл мәндерді сол қатардағы бірінші тік қорда тұрған сандарға, яғни (0, 5; 0, 866; 1) сәйкесінше көбейтіп, көбейтіндінің нәтижесін тордағы дәл
сол орынға орналастырады. Кейін әрбір тік қатардың мүшелерін қосып, он екі санды адламыз:
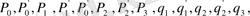 және олар келесідей орналастырамыз:
және олар келесідей орналастырамыз:
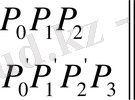
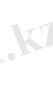
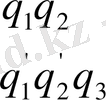 (ІІ)
(ІІ)
Бұл тік қатарларда тұрған соандарды қосып, алып, мына схемаға ие боламыз:
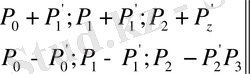
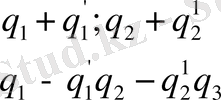 (ІІІ)
(ІІІ)
Онда бұл схемада тұрған сандар төмендегі схемадағы сәйкесінше коэффициенттердің мәндерін береді.
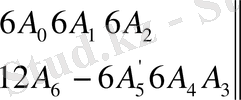
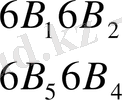
(2. 4) теңдіктерімен өрнектелген әрекеттер көсетілген ірекеттер тізбегіне пара-пар екенін тексері оңай.
Есептеулер нәтижелері бірден барлық
 және коэффиценттерін беретінін атап өту қажет.
және коэффиценттерін беретінін атап өту қажет.
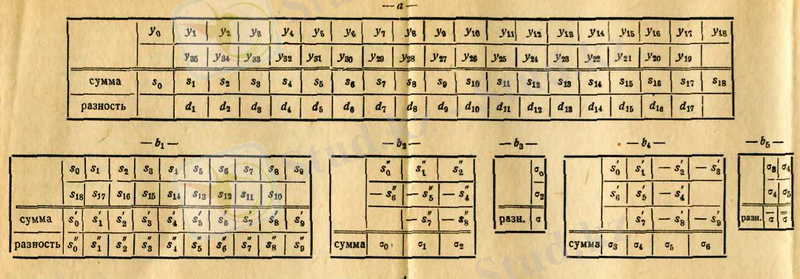
мысал: 1-фигура көрсетілген қисықтың ординатасы 12 тең аралықты бөлуде у 0 - ден бастап у 11 - ді қоса келесі мәндерге ие:
+20; +31; +38; +37; +22; -13; -50; -48; -25; -10; +3; +10.
Сондықтан келесіні жазамыз;

u қатарын келесі түрде қайта жазып, бір қатарда тұрған сандарды
қосып, аламыз.

v қатарымен де дәл солай етеміз;

Бұл нәтижелер (ІІ) схемаға қойып, сәйкесінше 05:0, 866:1, мәндеріне көбейтіп келесі нәтижені аламыз:
Бұдан соң (ІІІ) схемаға сәйкес келесіге ие боламыз:
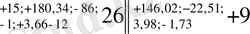
нәтижесінде
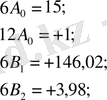
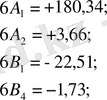
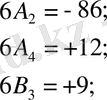
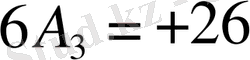
Дербес жағдай ІІ. 2v=24 болсын. Бөлінетін қисық Ох осіне қатысты кососимметриялы. Онда жұп ретті гармоникалар жоқ болады. Бұл жағдайда келесідей әрекетті орындаймыз.
Ординаталардың қатар мәндерін алдыңғыдай жазамыз.

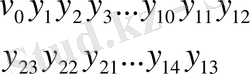
Қосындылары
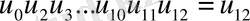
Айырымы
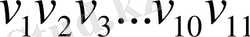
Онда (2. 3) теңдіктерін келесі түрде жазуға болады
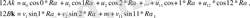
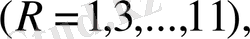 (2. 5)
(2. 5)
мұндағы
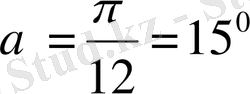
Бұл жағдайда қисықтар ерекше сипатына қарай R тақ сан болғандықтан, қатрдың басы мен соңынан тең қашықтықтағы мүшелерінің косинусын, яғни
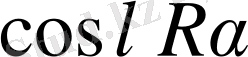 және
және
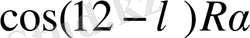 алып, келесіге ие баламыз.
алып, келесіге ие баламыз.

яғни қатардың басы мен соңынан тең қашықтағы косинустар абсолют мәні бойынша тең, таңбалары бойынша қарама-қарсы.
Дәл осылай,

теңдігін аламыз, яғни қатардың басы мен соңынан тең қашықтықтағы синустар абсолют мәндері және таңбалары бойынша бірдей.
Сондықтан былай жазамыз:
Айырмалар
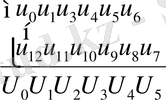 Қосындылар
Қосындылар
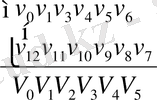
онда (2. 5) теңдеуінің орнына
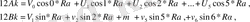 (2. 6)
(2. 6)
теңдіктерін аламыз, мұндағы R = 1, 3, …, 11
-1; 0; +1; +2; +3; +4 мәндерін қабылдайтындай R -мен R=2h+3 қатынасы арқылы h шамасын есептеуге енгіземіз.
Сонда келесіге ие боламыз.
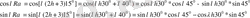
Егер
 =
=
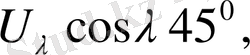
 =
=
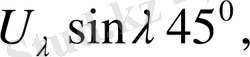
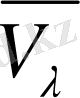 =
=
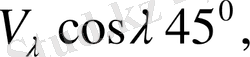
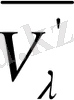 =
=
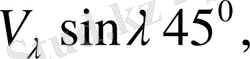
деп белгілесек, онда
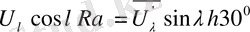 аламыз.
аламыз.
Сондықтан (2. 6) теңдіктерінің орнына
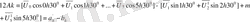
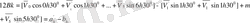
деп жазңға болады.
Егер R - ны h-пен алмастырсақ, ah пен
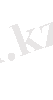
 мәндерін (2. 5) теңдігінен алынған А
4
мәндерімен, сонымен қатар b пен
мәндерін (2. 5) теңдігінен алынған А
4
мәндерімен, сонымен қатар b пен
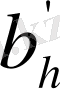 мәндерін B
h
мәндерімен салыстыра отырып, бұл формулалардың ұқсастығын көреміз. Сондықтан кейінгі топтауды дәл алдыңғыдай етіп орындаймыз, яғни келеміні аламыз.
мәндерін B
h
мәндерімен салыстыра отырып, бұл формулалардың ұқсастығын көреміз. Сондықтан кейінгі топтауды дәл алдыңғыдай етіп орындаймыз, яғни келеміні аламыз.
Косинустық мүшелер үшін Синустық мүшелер үшін
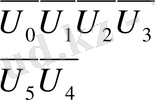
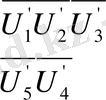
қосындылар
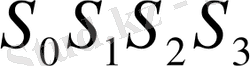 қосындалар
қосындалар
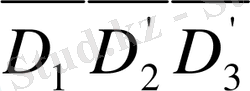
айырмалар
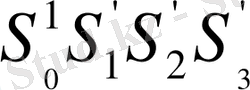 айырмалар
айырмалар
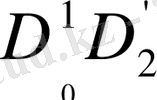
 мен
мен
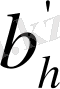 үшін аналогиялы болады.
үшін аналогиялы болады.
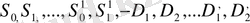 сандары (І) схемадағы
сандары (І) схемадағы
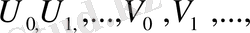 сандары ның орнына қойып, сәйкесінше 0, 5; 0, 866 және 1-ге көбейтеміз.
сандары ның орнына қойып, сәйкесінше 0, 5; 0, 866 және 1-ге көбейтеміз.
Кейінгі топтаулар дәл алдыңғыдай орындалады.
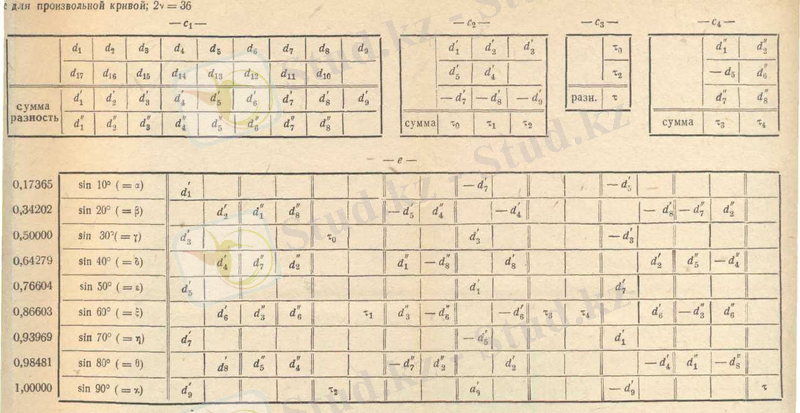
Рунге схемаларын. Эмде нақтылады. Төменде бұл схемалар кездейсоқ қисық пен
 және
және
 бөліну сандары үшін келтірілген. (қосымшаны қараңыз) .
бөліну сандары үшін келтірілген. (қосымшаны қараңыз) .
Кездейсоқ қисық үшін Рунге - Эмге топтау схемасы,

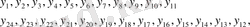
Қосындылар
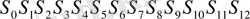
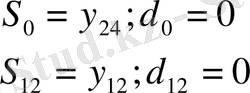
Айырмалар
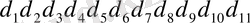

Қосындылар
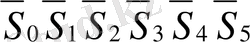
Айырмалар
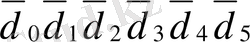
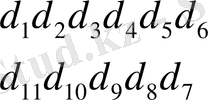
Қосындылар
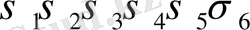

Айырмалар
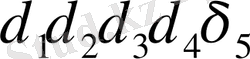
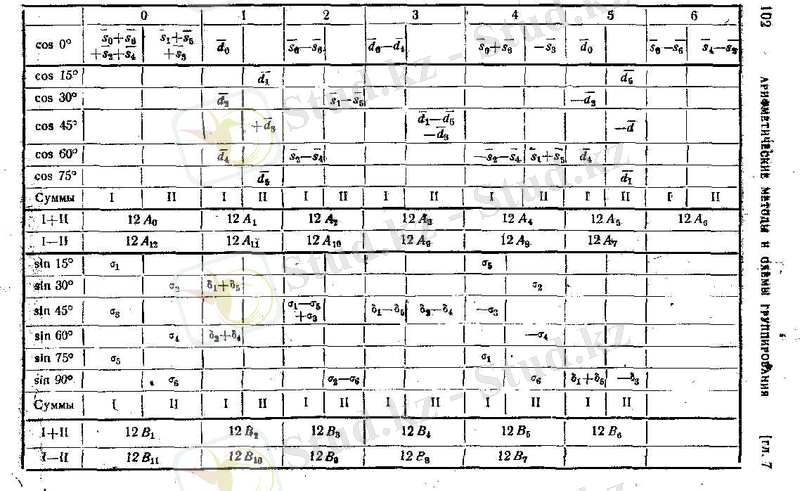
Кездейсоқ қисық үшін Рунге - Эмденің топтау схемалары;

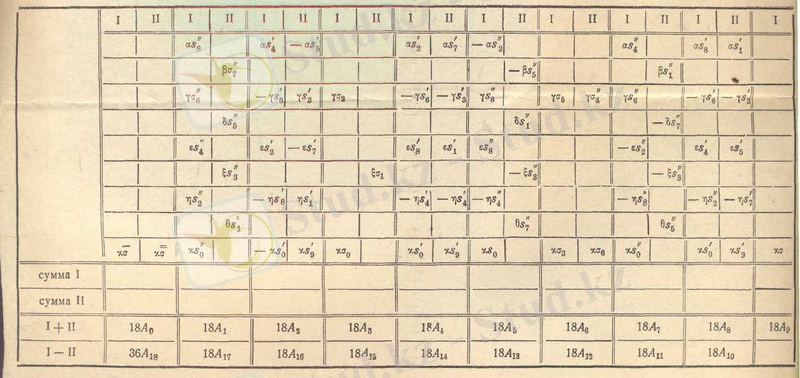
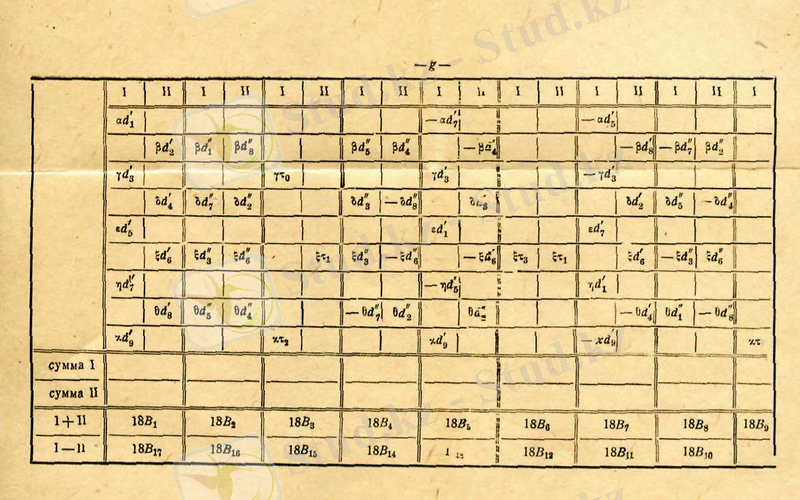
Схемаларды пайдалану үшін схемаға дәл тор дайындайды. Бұл тордан негатив секілді жасайды, яғни схемада толтырылмаған тор көздерді штрихтайды. Осылай дайындалған бланк-негативті есептеулердің нәтижелерімен схемада көрсетілген ретпен штрихталмаған тор көздерге берілген сандарды жазып толтырамыз.
Бұдан соң әрбір жазылған санды берілген қатарға сәйкес косинус немесе синустың мәніне көбейтіп, көбейтіндіні жаңа тордағы дәл осы орынға жазады. Содан қатарда схемада көрсметілгендей орналасқан мүшелердің қосындысының қосындысы немесе айырымын алып,
 немесе
немесе
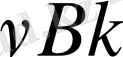 мәндерін аламыз.
мәндерін аламыз.
С. В. Абальник Рунгенің топтау схемасының басқа түрөзгерісін келтіреді.
§7 Рунге топтауын жалпылау
§ 6 параграфта қарастырылған топтау схемаларды жалпы түрге келтіруге болады.
Эквидистантты бөлінулер саны алдыңғыдай 2
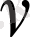 - ға тең болсын. жоғарыдағыдай 2
- ға тең болсын. жоғарыдағыдай 2
 ординаталарды екі қатарға орналастырамыз да, бірінен соң бірі тұрған ординаталардың қосындысы мен айырмаларын аламыз.
ординаталарды екі қатарға орналастырамыз да, бірінен соң бірі тұрған ординаталардың қосындысы мен айырмаларын аламыз.
Сонда келесіні аламыз.
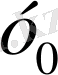
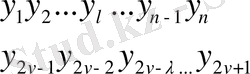
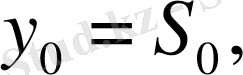
қосынды
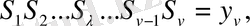
айырмалар
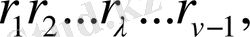
мұндағы
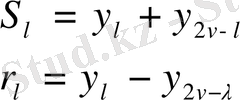

- теңдіктерін жалпылап, келесіні аламыз:
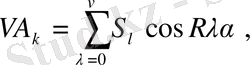
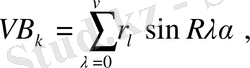
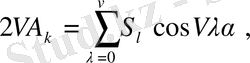 мұндағы
мұндағы
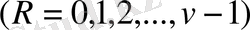
v жұп сан делік, яғни периодтың бөліну саны 4-ке еселі болғандықтан,
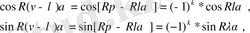 (2. 7)
(2. 7)
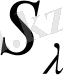 сандарын алдыңғыға аналогиялы түрде екі қатарға орналастырамыз және бірінен соң бірі тұрған сандардың қосындысы мен айырмаларын аламыз:
сандарын алдыңғыға аналогиялы түрде екі қатарға орналастырамыз және бірінен соң бірі тұрған сандардың қосындысы мен айырмаларын аламыз:
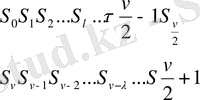
қосындалар
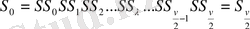
Айырмалар
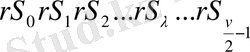 , мұндағы
, мұндағы
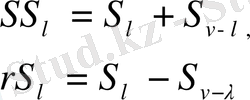 ,
,
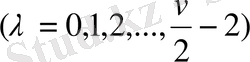
- негізде келесіге ие боламыз:
R - ның жұп мәндері үшін:
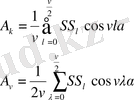
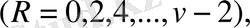 (2. 8)
(2. 8)
R - ның тақ мәндері үшін:
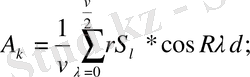
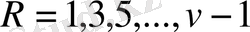
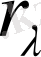 cандарын аналогиялы түрде топтар, келесіні аламыз:
cандарын аналогиялы түрде топтар, келесіні аламыз:
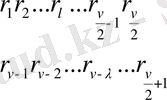
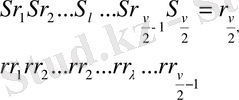
онда
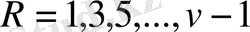 үшін
үшін
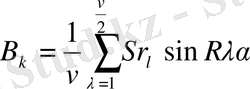
және
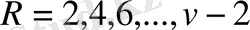 үшін
үшін
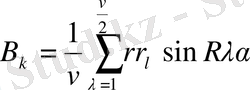 екенін аламыз.
екенін аламыз.
Әрі қарай,
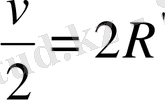 жұп сан делік, яғни периодтың бөліну саны 8-ге еселі
жұп сан делік, яғни периодтың бөліну саны 8-ге еселі
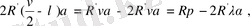
болғандықтан
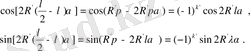 болады.
болады.
Сондықтан
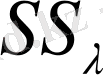 сандарын
сандарын
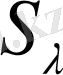 қатарына аналогиялы түрде екі қатарға орналастырып, бірінен соң бірі тұрған сандардың қосындысы мен айырмаларын аламыз. Нәтижесінде келесіні аламыз.
қатарына аналогиялы түрде екі қатарға орналастырып, бірінен соң бірі тұрған сандардың қосындысы мен айырмаларын аламыз. Нәтижесінде келесіні аламыз.
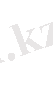

Қосындылар
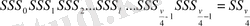
Айырмалар
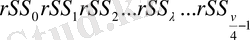
(2. 7) мен (2. 8) теңдіктеріне аналогиялы түрде мына формулаларды аламыз.
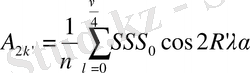
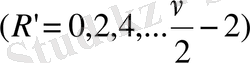
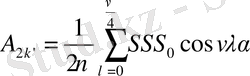
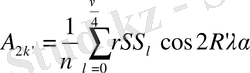
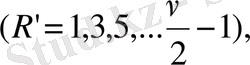
Дәл осылай келесіні аламыз.
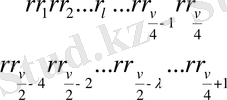
қосындылар
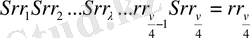
айырмалар
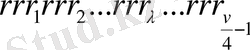
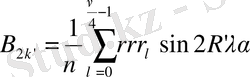
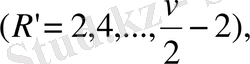
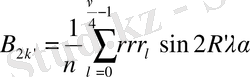
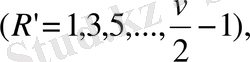
Есептеуді қысқатуды әрі қарай жалғастыруға болады. Бұл үшін
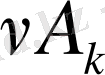 өрнегінде жұп индексті қосылғыштар қосындысын
өрнегінде жұп индексті қосылғыштар қосындысын
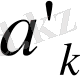 деп, ал тақ индексті қосылғыштар қосындысы
деп, ал тақ индексті қосылғыштар қосындысы
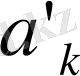 арқылы белгілейміз, сондықтан
арқылы белгілейміз, сондықтан
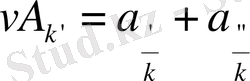
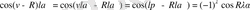
болғандықтан
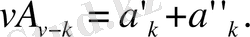
Егер әрі қарай,
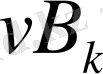 өрнегіндегі жұп және тақ индексті қосылғыштардың қосындысын
өрнегіндегі жұп және тақ индексті қосылғыштардың қосындысын
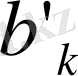 және
және
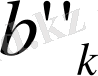 арқылы белгілесек, онда аналогиялы жолмен
арқылы белгілесек, онда аналогиялы жолмен
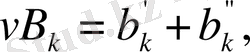
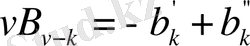
теңдіктерін аламыз.
Сондықтан жоғарыда келтірілген формулалардан келіп шығып
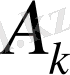 мен
мен
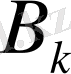 коэффиценттерін тікелей есептеудің орнына алдын ала
коэффиценттерін тікелей есептеудің орнына алдын ала
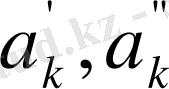 және
және
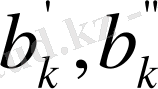 қосындыларын алдын ала есептеп алуға болады. Онда
қосындыларын алдын ала есептеп алуға болады. Онда
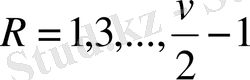 болғанда келесіні аламыз.
болғанда келесіні аламыз.

Тарау ІІІ. Шаблондар
§ 8 Шаблондардың қолданылуы
Қисықтың Ортақ көбейткішті ординаталарын топтаудың арифметикалық әдістері бұл ординаталар немесе олардың көбейткіштерін қандай да топтарға сұрыптаудың таза механикалық тәсілдерімен алмастырылуы мүмкін. Бұл топтаудың механикалық тәсілдерінің арасында ең алдымен шаблондарды қолдануға негізделген тәсілдерді атап өту қажет. Олардың көбінің қолданылуының жалпы принципіне мынадай. Қарастырылып отырған жіктеуде кездесетін синустар мен косинустардың барлық мәндерін матрица деп аталатын негізгі бетке белгілі бір ретпен тізіп жазамыз. Кейін қандайда бір
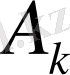 немесе
немесе
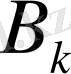 коэффицентін анықтау үшін кардон парағынан құралған және матрицадағы септеу үшін қажетті
коэффицентін анықтау үшін кардон парағынан құралған және матрицадағы септеу үшін қажетті
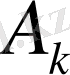 немесе
немесе
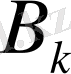 элементтері шығатын тесіктері немесе «терезешелер» бар алдын-ала дайындалған шаблондарды матрицаға беттестіреді.
элементтері шығатын тесіктері немесе «терезешелер» бар алдын-ала дайындалған шаблондарды матрицаға беттестіреді.
Әр түрлі шаблондарда тесіктер әр түрлі жерде орналасқандықтан беттестігенде әр түрлі элементтер топтары шығады. Біз мұнда Германн, Лемон шаблондар жүйесін сипаттаймыз.
§ 9 Германн мен Леман шаблондары
Германн шаблондарын құру келесіден тұрады. Түгел базис, немесе қисық толқынының ұзындығы 40 тең бөліктерге бөлінеді және кейін барлық 40 эквидистантты ординаталар
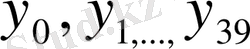 өлшенеді. Бұл ординаталарды көбейту керек болған косинус пен синустың барлық мәндері 11 мүшеден тұратын келесі қатарға енді:
өлшенеді. Бұл ординаталарды көбейту керек болған косинус пен синустың барлық мәндері 11 мүшеден тұратын келесі қатарға енді:

Сондықтан келесідей етеміз:
 - ден
- ден
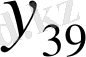 -ға дейінгі барлық ординаталардың бір тік қатарға жазып, оларды
-ға дейінгі барлық ординаталардың бір тік қатарға жазып, оларды
 - қа көбейтіп, 2-тік қатарға орналастырамыз; дәл
- қа көбейтіп, 2-тік қатарға орналастырамыз; дәл
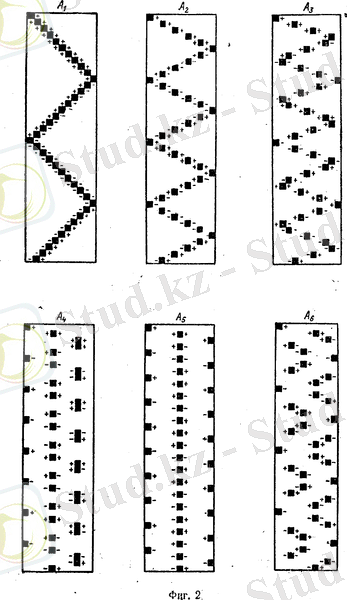
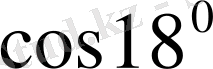 - қа көбейтіп солай 3-тік қатар алынады және т. б. Нәтижесінде 40 қатар, 11 тік қатардан құралған матрица пайда болады және 11-тік қатар 0-ден тұрады. Бұл матрицаға қатарынан шаблондарға беттестіреді (ФИГ. 2) . Әр бір
- қа көбейтіп солай 3-тік қатар алынады және т. б. Нәтижесінде 40 қатар, 11 тік қатардан құралған матрица пайда болады және 11-тік қатар 0-ден тұрады. Бұл матрицаға қатарынан шаблондарға беттестіреді (ФИГ. 2) . Әр бір
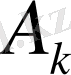 Фурье коэффициентіне өзінің шаблоны сәйкес келеді. 2- фигурада шаблонның оң жағында. Соңғы таңбаны шаблонның келесі бетіне дәл сол орынға қайта жазу қажат; онда әр бір шаблон бір ретті Фурьенің екі коэффицентін анықтау үшін пайдаланылуы мүмкін. Схеманы бір сәйкес беттің матрицасына беттертіріп, А
к
-ны анықтау үшін сандарды алады, ал дәл осы шаблонды келесі беттің матрицасына беттестіріп, B
k
-ны анықтау үшін сандар алады; мұнда тор көздің сол жағында тұрған таңбаланы алу қажет.
Фурье коэффициентіне өзінің шаблоны сәйкес келеді. 2- фигурада шаблонның оң жағында. Соңғы таңбаны шаблонның келесі бетіне дәл сол орынға қайта жазу қажат; онда әр бір шаблон бір ретті Фурьенің екі коэффицентін анықтау үшін пайдаланылуы мүмкін. Схеманы бір сәйкес беттің матрицасына беттертіріп, А
к
-ны анықтау үшін сандарды алады, ал дәл осы шаблонды келесі беттің матрицасына беттестіріп, B
k
-ны анықтау үшін сандар алады; мұнда тор көздің сол жағында тұрған таңбаланы алу қажет.


- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz