Инженерлік сызбаны модульдік технология арқылы оқыту

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 61 бет
Таңдаулыға:

инженерлік сызбаны модульдік технология арқылы оқыту

Оқу әдістемелік құрал

Павлодар
ӘОК 744 (075)
ҚБК 30.11
Т 75

С Торайғыров атындағы Павлодар мемлекеттік университетінің ғылыми
кеңесі баспаға ұсынған

Рецензентер:
Бейсембаев М.К. - т.ғ.к., доцент, Павлодар мемлекеттік
педагогикалық институтының ректорының орынбасары.
Жумабаева З.Е. - п.ғ.к., С Торайғыров атындағы Павлодар
мемлекеттік университеті

Т 75 Темербаева Ж.А.
Инженерлік сызбаны модульдік технология арқылы оқыту: оқу әдістемелік
құрал. – Павлодар: Кереку, 2008. – 85 б.

ISBN

Графикалық пәндерді инновациялық технологиямен оқыту – қазіргі жоғары
оқу орнындарында басты орын алады. Автор заманға бейімдеу мақсатында оқу-
әдістемелік құралын модульдік технология қағидасымен құрастырған. Бұл
беріліп отырған ғылыми еңбек Қазақстанның білімдендіру кеңістігінде
бәсекелестікте жеңетін, жан-жақты дамыған жаңа форматтың тұлғасын
тәрбиелеуге және оқытуға көмегін тигізетін нұсқаулар. Басты мақсаты –
графикалық пәндерді оқыту үдерісін жеңілдету жолы.

ӘОК 744 (075)
ISBN
ҚБК 30.11

© Темербаева Ж.А., 2008
© С.Торайғыров атындағы Павлодар мемлекеттік университеті, 2008
Алғы сөз

Оқыту үдерісінде жаңа инновациялық технологияларды заман талабына сай
енгізу білім берушілердің парызы болып саналады. Осыған орай, студентерді
кредиттік оқу жүйесіндегі модульдік технология арқылы оқыту дидактикасын
жасаудың маңызы өте зор. Білімденуде дидактиканы жетік меңгерген жеке
тұлғаның ой-санасы қоғамдық талаптар деңгейінде іс-қимыл көрсетіп,
қиындықтар мен бөгеттерден өтуде біліктілік пен табандылықтың үлгісін
танытады.
Мемлекет көздеген тактика мен стратегиясына инновациялық технологиямен
білім беру мазмұны мен оқыту жолын айқындайтын, ұтымды нәтижеге жедел қол
жеткізетін тиімді әдістеме түбегейлі, толыққанды зерттелмеген, жоқтын қасы.
Сондықтан Студенттерді кредиттік оқу жүйесіндегі модульдік технология
арқылы оқытудың дидактикасы деп алынуы еңбектің мәртебелі тұсы.
Инженерлік сызбаны оқыту мәселелерін зерттеу отандық педагогиканың
оқыту әдістемелік жүйесін дамытады. Инженерлік сызбаны инновациялық
технологиямен оқыту, оны дамыту мен шындық оқыту жүйесінің салиқалы,
салмақты болуына айтарлықтай нәр болып, түлғаны тәрбиелейді. Осы тұрғыдан
автордың Студенттерді кредиттік оқу жүйесіндегі модульдік технология
арқылы оқытудың дидактикасы атты монографиялық жұмысы бүгінгі күннің
өзекті мәселесіне арналған. Әдістеме ұғымына жан-жақты анықтама беріп, бұл
зерртеу жұмысына дейінгі бағыттағы еңбек еткен ғалымдардың тұжырым-
түйіндері зерделегені аңғарылады.
Инженерлік сызбаны оқытудың әдістемелік тұжырымдамасының жасалуы-
зерделенген нысанның көрсеткіші.
XXI ғасырда білім берудің мазмұнды болуына толық мүмкіндіктер ұдайы
жасалып келеді. Оқыту үдерісінің сапалы мәні әр студент білімнің ғылыми
негізін даралық қабілетте қабылдауынан байқалады. Педагогикалық білім
берудің мазмұнында (жоғағы оқу орнында) бейнеленген педагогикалық
зерттеулердің нәтижесі парадигманың, яғни оқыту іс-әрекетінің жаңа
көзқараста білімдік жинақталған ұстанымдарында стандартқа сай студенттер
сұранымына, білім беру қызметінің сапасына байланысты нәтижені бағдарлайды.

Осындай парасатты іс-әрекетті тәжірибеде нәтижелі бағдарлауға нұсқа
болатын монографияда қамтылған ғылыми-теориялық негіздер студенттердің
ғылыми-біліми еңбегін оңтайлы ұйымдастырда пәрменді іс-әрекет құру бейіміне
көңіл бөлініп, оқыту қызметінің шарықтау шегі көрсетілген.
Зерттеу барысында берілген нәтижелер зерттеу мәселесін әдістемелік
тұрғыда дәйектеумен, ең өнімді де ұтымды тәсілмен орнымен қолданумен,
тәжірибеде негізделген жаңалығымен бекітілген жұмыстың негізгі нысанасы.
Автор көп жылдан бері сабақ беріп жұрген ұстаз. Бұл қызметінен
зерттеуші республикалық-халықаралық конференцияларда, педагогикалық
оқуларда әдістемелік нұсқаулықтары мен құралдарын кқпшілік оқытушы-
профессор қауымына ұсынған.
Қорыта айтқанда, Инженерлік сызба пәнің модульдік технология арқылы
оқыту тақырыбына жазылған еңбек әдістімелік, теориялық, тәжірибелік
тұрғыда қойылатын талаптарға сай деген ойымызды білдіреміз.

Жұматаева Е.

Кіріспе

Білім мен ғылымды меңгерген тұлғаның өмір сүргіштік қорғанысы,
заманның өзгерісті кезеңдерінде төзімділігі мен табандылығы, қоғамдағы
мүдделерге ілесуі, өзінің әрдайым өнімді іске бағдарлауы секілді
көрсеткіштері басымдықта болып келеді.
Осындай сүбелі істердің қарқынды тұрғыда жүзеге асуы мақсатында Ел
Президенті Н.Ә.Назарбаев халқына Жолдауында айтылған Қазақстанды әлемдік
озық 50 елдің қатарына жеткізу ұстанымына сай жаңа әлеуметтік-экономикалық
жағдай жасау, ұлттық мәдени өрісінде халықаралық және Еуропалық тенденция
негізіндегі оқыту жүйесіне көшуге бағдарлап отыр [2]. Бұл мақсатқа жетудің
сара жолы отандық, әлемдік озық ойлы, жаңашыл, ілгерішіл ғалымдары мен
қоғам қайраткерлері, кәсіби құзыретті мамандары бірыңғай инновациялық білім
кеңістігін жасау және оның мәселесі ең көкейкесті де, қиындық тудыратын да
шара деп есептейміз.
Жоғары оқу орындарында Инженерлік сызба, пәнін оқытудың бүгінгі күні
маңызы ерекше. Бірақ, өкінішке орай, жоғары оқу орындарында оқыту іс-
әрекетіне қатысты білімденудің инновациялық технологияларын ұтымды қолдану
мүмкіндігі әлі де болсын төмен екенін мойындаған орынды. ХХІ ғасырда білім
және ғылым саласындағы болып жатқан өзгерістер болашақ мамандарды даярлауда
оқытушы-профессор құрамына жаңа міндеттер қойып отыр. Соның бір дәлелі –
оқыту үдерісін кредиттік технологиямен құру. Кредиттік технологиямен жоғары
оқу орындарында сабақ беру іс-әрекеті кейінгі жылдары тәжірибеде сыннан
өтуде.
Жоғары оқу орындарында оқыту үдерісіндегі бүгінгі күн талабын
қанағаттындыру тұрғысында зерделеп қарасақ, бөлінген сағаттың тек 10
пайызына: бірінші, теориялық материалдарды сыйымды ету, ірілендіру тек
оқытушы-профессорлардың асқан шеберлігінің ұшқырлығымен орындалады. Екінші,
студенттер мен оқытушы-профессорлардың үйлестірушілік және кеңесшілік
жұмысына жалпы жұмыс сағатының 20 пайызы жұмсалады. Ал үшінші студенттердің
өздігінен жеке жұмысына жалпы сағаттың 70 пайызы пайдаланады. Нәтижесінде
оқытушы-профессор құрамы өтілуге тиісті стандарт шегіндегі оқулықтың үлкен
тарауларын модельге, үлгіге салып, оның бір үлгіге жататынын ой елегінен
тұтастай өткізу арқылы сабақтың тұтас жүйесінің заңдылығын сақтауға және
оның ішкі бірліктерінің ұштастығына студенттердің көзін жеткізеді. Аталған
бір оқулық материалын бір үлгі деп есептесек, үлгінің әрбір тармағының кіші
құрамдарға жіктелуі модульдік түзілімдер құрауға мүмкіндік туғызады.
Сөйтіп үлгіден модульдер туындап, әрбір жеке-жеке тақырыптардың туыс,
түбірлестерінің жеке даралық сапа көрсеткіштерінің жіктемелері шығады.
Зерттеу жұмысымыздың ең маңызды тұсы да осы модельге және модульге
мемлекеттік стандарт шегінде ұсынылған типтік бағдарлама нысанында құралған
жұмыс бағдарламасын аталған талапқа сәйкестендіру болып табылады.
Кредиттік жүйеде білім берудің жаңа парадигмасы оқу – қалай оқығаныңа
қарай, өзін-өзі дамыту, өмір бойына оқу болып өзгерді. Жаңа жүйеде
оқытушы студенттерге өздігінен білім алудың түрлі әдістері мен жолдарын
көрсете отырып, студенттің өз бетімен жасайтын танымдық әрекетінің
ұйымдастырушысы болып табылады. Жоғары оқу орнының жұмысының нәтижесі –
білім алушылардың кәсіби білім беру бағдарламалары бойынша білімдерінің
сапасы, ал мамандарды даярлаудың сапасының өлшемі – мемлекеттік білім беру
стандартындағы біліктілік талаптарға сәйкес анықталған теориялық дайындық
деңгейі арқылы бағаланатын маманның кәсіби құзіреттілігі. Жоғары кәсіби
білім берудің мақсаты еңбек нарқы қажетіне сай мамандарды даярлау
болғандықтан, бұл Болон үдерісінің негізінде жатқан қағидалармен, оның
ішінде оның басты қағидаларының бірі білім беру сапасын бақылаумен
үйлеседі. Әрі сапаны бақылау оқыту мерзімі мен оқыту мазмұнына емес,
маманның кез келген еуропалық мемлекетте жұмыс істеуге даярлығына
негізделеді.
Білім беру жоғары оқу орындарында оқу үдерісіндегі оқытушы мен
студенттің өзара танымдық қызметінің деңгейлігіне бағынады. Оқытушы типтік
бағдарламаның мамандандырылған мінездемедегі көрінісімен біріктіріп, өзінің
жұмыс бағдарламасын құрастырады. Дидактикалық нысанның оқу жоспары
нақтыланып, блоктарға, модульге жіктеліп, оның пәніне орай баспадан жарық
көрген оқулықтар мен оқу құралдарының бағдарламадағы көрінісін тәжірибеде
қолдануға қозғаушы күш рөлін атқарады.
Студенттерді оқытуда Инженерлік сызба пәні бойынша білімді
қалыптастыру бүгінгі жоғары оқу орнының студенттері – болашақта мамандардың
жалпы мәдениетін қалпына келтіруді көзделеді.
Кредиттік оқыту жүйедегі оқытуға тиісті Инженерлік сызба пәнінен
оқулықтар бүгінгі жаңа технологияның талап-мүддесін қанағаттандыра
алмайды.
Осы тұжырымдамызды нақтылау үшін жаңа технология қағидасымен құрылған
оқулықты беруді орынды деп есептейміз.

Шартты белгілер

1. А,В,С,Е,Ғ;... 1, 2, 3 ..., қеңістітік нүктелер латын алфавитының бас
әріптерімен белгіленеді. Көмекші нүктелерді цифрлармен белгілеу керек.
2. а, в, с, д, е, і .., кеңістік сызықтары, латын алфавитының
жазба әріптерімен белгіленеді;
3. L, β, γ, Σ, Ğ... , жазықтықтар грек алфавитының жазба әріптерімен
белгіленеді.
П – проекция жазықтығы;
П 1 – горизонталь проекция жазықтығы;
П 2 – фронта ль проекция джазықтығбы;
П 3 – профиль проекция жазықтығы;
П 4, П 5 – қосымша проекция жазықтықтары;
4. Х, У, Z – проекция осьтері;
5. Нүктелер проекциясы:
П 0 – А,0 В0 ,С0..., еркін жазықтыққа
П 1 – А, В, С ..., горизонталь жазықтығына
П 2– А 2, В 2, С 2..., фронталь жазықтығына
П 3 – А 3, В 3,С 3..., профиль жызықтығына
П 4– А 4, В 4, С 4..., қосымша жазықтықтарға
6. Литерлар:
t - горизонталь түзуі;
f - фронталь түзі;
p - профиль түзуі;
7. Жазықтықтардың іздерінің белгілері:
t 0L -L
f 0L-L
p 0L-L
X 1 YL ZL – іздің жазықтықпен қиылысу нүктесі.

1 Модуль. Инженерлік сызба пәні

1.1 Блок геометриялық формалар: орталық және параллель проекциялы
сызбаларды алудың әдістері
Фигураның белгілі бір ереже бойынша жазықтыққа түсірілген кескіні
проекция деп аталады. Егер затта жазықтыққа кескіндеген кезде
проекциялаушы сәулелер бір нүктеден тарайтын болса,онда мұндай әдісті
орталық проекциялау деп атайды. (1а сурет). Орталық проекциялау әдісі
сәулет және бейнелеу өнірінде кеңінен қолданылады.Орталық проекцияны кейде
конустық немесе перспективалық проекция деп атайды.
Егер нәрсе кескінің алу өзара параллель проекциялаушы сәулелер
қолданылса,онда мұндай әдісті параллель проекциялау деп атайды. (1б
сурет).
Түзу мен жазықтықтың ортақ нүктесі олардың қиылысу нүктесі деп айтады.

Мысал : S

а)

C E

D

E1

C 1 D1

П1

б)

C D
E S

C 1 D 1
E 1

П1

1 сурет – Проекциялау тәсілдері: а) орталық проекциялау
(S – проекция центрі); б) параллель проекциялау (S – проекция бағыты); П –
проекция жазықтығы; C, D, E – проекциялаушы нүктелер
Тапсырма:
1) Проекциялау аппараты: S – проекциялау центрі және П – проекциялар
жазықтығы белгілі. Берілген АВС үшбұрышының екі төбесінің проекциялары
белгілі деп қарастырайық, оның центрлік проекциясың салуды аяқтау керек (2
сурет).

S

A B

C

B1
C1
П1

2 сурет

Сұрақтар

1. Проекция деген не?
2. Орталық проекциялау деген не?
3. Параллель проекциялау деген не?

Әдебиеттер

1 Есмуханов Ж.М., Қонақбаев Қ.Қ., Сызба геометрия. – Алматы: Мектеп,
1968 .
2 Есмуханов Ж.М., Мақышев Е.М, Есмуханов Е.Ж. “Сызба геометрия
есептері”. – Алматы: “Білім”, 1995.
3 Гордон В.О., Семенцов – Огиевский М.А., “Курс начертательной
геометрии”. – М. : “Наука”, 1968.
4 Климухин Ю.И.Начертательная геометрия. – М. : Стройиздат, 1978.
5 Короев Ю.И. Начертательная геометрия. – М. : Строийиздат, 1987
1.2 Блок. Тік бұрыштап проекциялау әдісі
Проекциялау бағыты S проекциялар жазықтығына перпендикуляр болатын
параллель проекциялардың жеке түрін тік бүрыштап проекциялау дейді.
Берілген АВ түзуінің П жазықтығындағы кескінін салу үшін, одан П1
жазықтығына перпендикулыр түсірейік. Жазықтыққа перпендикуляр деп сол
жазықтықпен 90( бұрыш жасайтын түзуді айтады.
АВ түзуінен П жазықтығына түсірілген перпендикулярдың табаны А1В1
түзуі АВ түзуінің П1 жазықтығындағы тік бұрыш проекциясы (3 сурет).
Мысал

АВ түзуін П1жазықтығына тік бұрыштан проекциялау П – проекциялар
жазықтығы, АВ – проекциялатын түзу; (( - АВ түзуінің П1 жазықтығына
көлбеулік бұрышы.

3 сурет

Проекциялау бағыты S проекциялар жазықтығына перпендикуляр болатын
параллель проекциялардың жеке түрін тік бүрыштап проекциялау дейді.
Берілген АВ түзуінің П жазықтығындағы кескінін салу үшін, одан П1
жазықтығына перпендикулыр түсірейік. Жазықтыққа перпендикуляр деп сол
жазықтықпен 90( бұрыш жасайтын түзуді айтады.
АВ түзуінен П жазықтығына түсірілген перпендикулярдың табаны А1В1
түзуі АВ түзуінің П1 жазықтығындағы тік бұрыш проекциясы (3 сурет).

Тапсырма:

1) Берілген СD кесіндісің П1 жазықтығына тік бұрыштап
проекциялау керек (4 сурет).

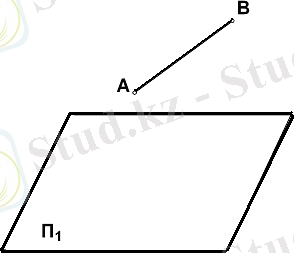
4 сурет

2) АВСD төрбұрыш берілген проекция жазықтығыны параллель, осы
төртбұрышты тік бұрыштып П1 жазықтығына проекциялау керек (5
сурет).

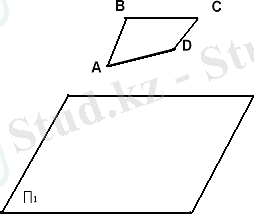
5 сурет
Сұрақтар

1. Тік бұрыштап проекциялау деп нені айтады?
2. Жазықтықта нәрсе кескіні қалай салынады?
3. Жазықтыққа перпендикуляр деп нені айтады?

Әдебиеттер

1. Ақпанбек Ғ. “Сызба геометрия” – Алматы, 1998.
2 Есмуханов Ж.М., Қ.Қ. Қонақбаев. Сызба геометрия. – Алматы: Мектеп,
1968.
3 Есмуханов Ж.М., Е.М.Мақышев, Е.Ж.Есмуханов. “Сызба геометрия
есептері”. – Алматы: “Білім”, 1995.
4 Четверухин Н.Ф. и др. “Начертательная геометрия”. – М. : “Высшая
школа”, 1963 .
5 Бубенников А.В. Начертательная геометрия. – М. : Высшая школа,
1985. – 288 .
6 Короев Ю.И. Начертательная геометрия.
– М. : Строийиздат, 1987

1.3 Блок. Қиғаш бұрыштан проекциялау
Егер өзара параллель проекциялаулы сәулелер проекция жазықтығына 90(С
– қа тең емес кез келген бұрыш жасай түсетін болса, онда мұндай әдіс қиғаш
бұрыштан проекциялау деп аталады (6сурет). 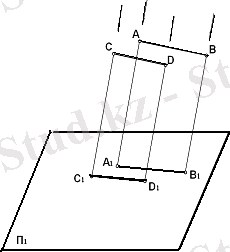6 сурет - Өзара параллель
AB және CD түзулердің қиғаш бұрышты проекциялары

Кеңістіктегі фигуралардың параллеь проекцияларындағы өзгерссіз
сақталатын қасиеттерін инварианттар деп атайды.
Проекциясы бойынша кеністіктегі нәрсенің пішінін ойша анықтау мүмкін
болмаса, мұндай кескіндерді қайтымсыз дейді. Нәрсенің пішіні,өлшесдері
ерекшеліктері туралы мағлұматтар сызба арқылы танылатын болса, сызба
қайтымды болады.

Тапсырма:

1) ЕF түзуін l жазықтығына қиғаш бұрышты проекциясын cалыңыздар
(7 сурет).

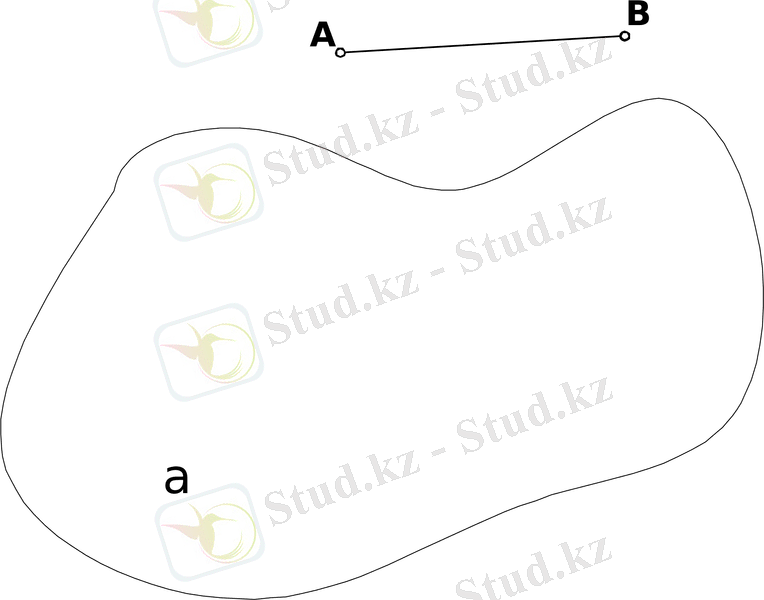
7 сурет

Сұрақтар

1. Қиғаш бұрыштап проекциялау деп нені айтады?
2. Жазықтықта нәрсе кескіні қалай салынады?
3. Қандай сызбаларды қайтымды немесе қайтымсыз дейді?
4. Инварианттар деп нені айтады ?

Әдебиеттер

1 Есмуханов Ж.М. Сызба геометрия есептері. – Алматы: “Білім”, 1995.
2 Есмуханов Ж.М., Мақышев Е.М., Есмуханов Е.Ж. Сызба геометрия
есептері. – Алматы: “Білім”, 1995 .
3 Гордон В.О., Семенцов – Огиевский М.А. Курс начертательной
геометрии. – М. : “Наука”, 1968.
4 Белов Н.В., Виквсель А.А. Начертательная геометрия. – Л. :
Стройиздат, 1969. – 231 с.
5 Арустамов Х.А. Сборник задач по начертательной геометрии. – М. :
Машгиз, 1965.

2 Модуль. Геометриялық элементтердің (нүктелер, түзулер және
жазықтықтар) кешенді сызбалар

2.1 Блок. Нүктенің проекциясы
Өзара перпендикуляр екі жазықтық кеністікті ширектер деп аталатың
төрт бөлікке бөледі (8 сурет).
Берілген нүктенің сызбасын алу үшін оны осы П1, П2 және П3
жазықтықтарына тікбұрыштап проекциялаймыз. Сонда нүктенің П1
жазықтығындағы тікбұрышты проекциясын оның горизонталь проекциясы, П2
жазықтығындағы тікбұрышты проекциясын оның фронталь проекциясы және П3
жазықтығындағы тікбұрышты проекциясын оның профиль проекциясы деп атайды.

П1 жазықтығын горизонталь проекциялар жазықтығы, П2 жазықтығын
фронталь проекциялар жазықтығы және П3 жазықтығын профиль проекциялар
жазықтығы деп айтады (9 сурет)
Кеністікте П1,П2 және П3 жазықтықтары 8 бөлікке бөледі.Осы бөліктерді
октанттар деп атайды.
Жазықтықтарды сызба жазықтығымен беттестіргенде шығатын кескінді эпюр
деп айтады (9 сурет) Кейде эпюр деудің орнына комлекстік сызба, немесе
сызба деп те айтады. Сызуда фронталь проекцияны алдынан қарағандағы
көрініс, горизонталь проекцияны үстінен қарағандағы және профиль проекцияны
сол жағынан қарағандағы көріністер деп атайды. Алдынан, үстінен және сол
жағынан қарағандағы көріністер негізгі көріністерге жатады. Осыған орай
эпюрді негізгі көріністер сызбасы деп те атайды.
Нүктенің фронталь және горизонталь проекцияларын қосатын түзу х осіне
перпендикуляр болады, яғни вертикаль орналасады. Сондықтан оны вертикаль
байланыс сызығы дейді. Ал фронталь және профиль проекцияларын қосатын түзу
z осіне перпендикуляр болады, яғни горизональ орналасады. Сондықтан оны
фронталь байланыс сызығы деп атайды. (А2 А1) – вертикаль байланыс сызығы;
(А2 А3) – горизонталь байланыс сызығы. Нүктенің фронталь және горизонталь
проекцияларының ара қашықтығы оның ординасы мен аппликатасының қосындысына
тең. Ал фронталь және профиль проекцияларының ара қашықтығы абциссасы мен
ординатасының қосындысына тең болады (10 сурет)

А2 А1 = y+z; А2 А3 = x+y

Бір нүктенің проекцияларын жалғастыратың түзулерді проекциялық
байланыс сызықтары деп атайды.
Мысал
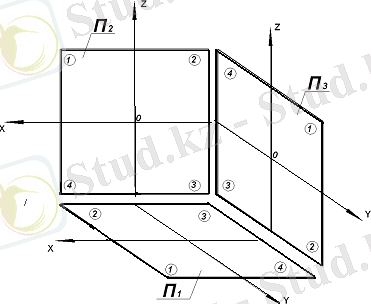8 сурет – Жазықтықтардан ширептері

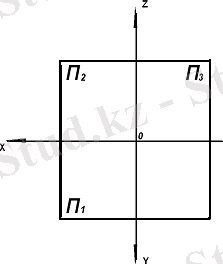
П1 – горизонталь проекциялар жазықтығы; П2 – фронталь проекциялар
жазықтығы; П3 – профиль проекциялар жазықтығы

9 сурет – Жазықтықтардың эпюрі

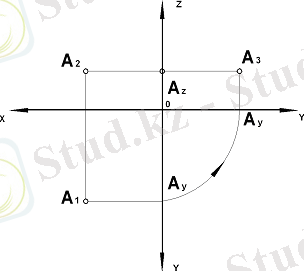
10 сурет – А нүктенің проекциялары

Тапсырма:
1) проекция жазықтықтары П1, П2, П 3 және А (25;40;50) нүктесі
берілсін. А нүктесін проекция жазықтықтарына проекциялаңыз;
2) берілген В (15;75;65) нүктесінің эпюрде горизонталь, фронталь
және профиль проекцияларын салыңыздар.

Сұрақтар

1. Октанттар деген не ?
2. Октанттар қайдан шығады ?
3. Проекциялық байланыс сызықтары деген не ?
4. Эпюрді оқу деп нені айтады ?
5. Нені проекциялық байланыс сызықтары деп айтады ?

Әдебиеттер

1 Есмуханов Ж.М., Қонақбаев Қ.Қ. Сызба геометрия.
– Алматы: Мектеп, 1968.
2 Есмуханов Ж.М., Мақышев Е.М., Есмуханов Е.Ж. Сызба геометрия
есептері. – Алматы : “Білім”, 1995.
3 Четверухин Н.Ф. и др. Начертательная геометрия. – М. : “Высшая
школа”, 1963.
4 Фролов С.А Начертательная геометрия. – М. : “Машиностоение”, 1983.
5 Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии.
– М. : “Наука”, 1968.

2.2 Блок. Түзулердің проекциясы
Түзудің проекцияларын алу үшін, оның кез келген екі нүктесінің аттас
проекцияларын түзулермен қосады.

Түзудің проекциясы – түзу болады.

Проекция жазықтықтарының ешқайсысна параллель емес түзулер жалпы
жағдайдағы түзулер деп аталады (11 сурет).
Бір проекция жазықтығына параллель болатын түзулер денгейлік түзулер
деп аталады (12 сурет).
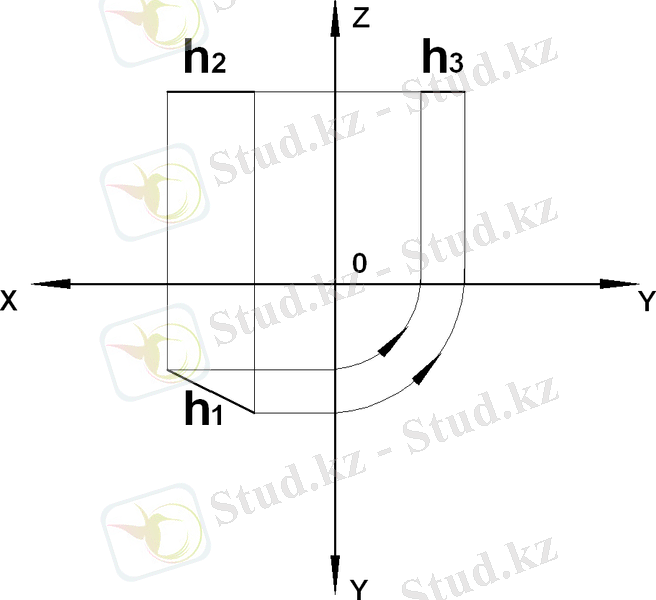
Горизонталь проекция жазықтығына параллель түзулер горизонталь деп
аталады және оны h әріппен белгілейді ( 12а сурет).
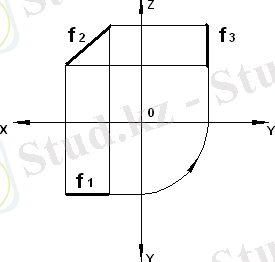
Фронталь проекция жазықтығына параллель түзулер фронталь деп аталады
және оны f әріппен белгілейді (12б сурет).
Профиль проекция жазықтығына параллель түзулер профиль деп аталады
және оны p әріппен белгілейді ( 12в сурет).
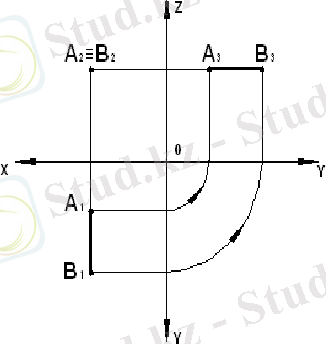
Кеністікте түзу проекция жазықтығына перпендикуляр орналасса, онда
проекциялаушы түзу деп аталады ( 13 сурет).
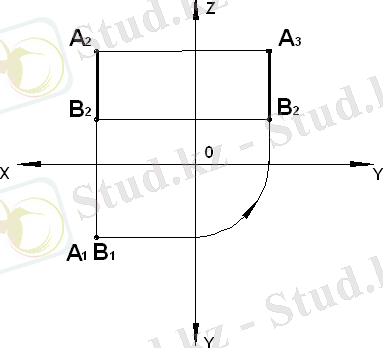
Горизонталь проекциялаушы түзу деп горизонталь проекция жазықтығына
перпендикуляр түзулурді айтады ( 13а сурет).
Фронталь проекциялаушы түзу деп фронталь проекция жазықтығына
перпендикуляр түзулурді айтады ( 13б сурет).
Профиль проекциялаушы түзу деп профиль проекция жазықтығына
перпендикуляр түзулурді айтады ( 13в сурет).
Мысал

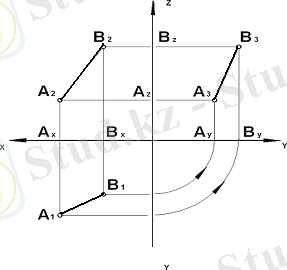
11 сурет – Жалпы жағдайдағы түзулер

а) б)

в)

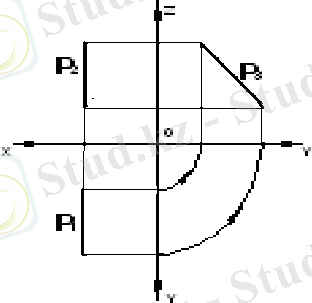
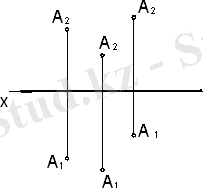
а) горизонталь; б)фронталь; в) профиль

12 сурет – Деңгейлік түзулер

а)
б)

в)

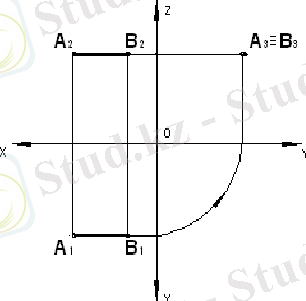
а) горизонталь проекциялаушы; б) фронталь проекциялаушы; в)профиль
проекциялаушы.

13 сурет – Проекциялаушы түзулер

Тапсырма:
1) Берілген координаттары бойынша АВ түзуін проекция жазықтықтарына
проекциялаңыз А (45;60;85); В (55;65;80);
2) А (25;30;45), В (45;85;60) нүктелерімен қандай түзу берілге? Эпюрін
салыңыз.

Сұрақтар

1. Денгейлік түзулердің ерекшіліктері неде?
2. Проекциялаушы түзулер деген не?
3. Жалпы жағдайдағы түзулер деп қандай түзулер аталады ?
4. Жалпы жағдайдағы түзулердің проекцияларының ерекшіліктері неде ?

Әдебиеттер

1 Ақпанбек Ғ. “Сызба геометрия”. – Алматы, 1998.
2 Есмуханов Ж.М., Қ.Қ. Қонақбаев. Сызба геометрия. – Алматы: Мектеп,
1968.
3 Арустамов Х.А. Сборник задач по начертательной геометрии. – М. :
Машгиз, 1965.
4 Фролов С.А “Начертательная геометрия” – М. : “Машиностроение”, 1983.
5 Климухин А.Г. Начертательная геометрия. – М. : Стройиздат, 1978. –
243 с.

2.3 Блок. Жазықтықтың проекциясы
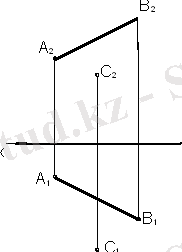
Кеністікте жазықтықтар шексіз деп есептеледі. Жазықтықтар кеністікте
орналасуына қарай жалпы келесі түрде беріледі (14 сурет):
а) бір түзудің бойында жатпайтын үш нүкте арқылы(14а сурет);
б) түзу және олан тысқара орналасқан нүкте арқылы(14б сурет);
в) қиылушы екі түзумен (14в сурет);
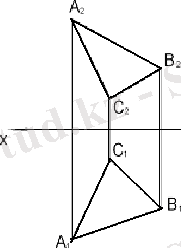
г) өзара параллель екі түзумен (14г сурет);
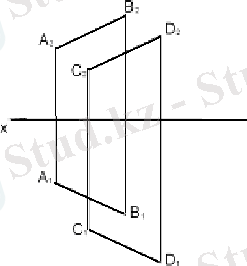
д ) жазық фигурамен (14д сурет);
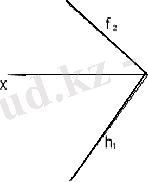
е) іздермен (14е сурет).

Мысал:

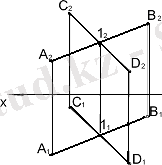
а) б)
в)

г) д) е)

а) бір түзудің ойында жатпайтын үш нүкте; б) түзу және олан тысқара
орналасқан нүкте; в) қиылушы екі түзумен; г) өзара параллель екі түзумен;
д) жазық фигурамен; е) іздермен .

14 сурет – Жазықтардың кеністікте орналасуы
Проекция жазықтықтарын параллель немесе перпендикуляр болатын
жазықтықтарды дербес жағдайдағы жазықтықтар деп атайды (15 сурет). Егер
берілген жазықтық горизонталь проекция жазықтығына перпендикуляр болса,
онда мұндай жазықтықты горизонталь проекциялаушы жазықтық деп атайды (15а
сурет). Егер берілген жазықтық фронталь проекция жазықтығына перпендикуляр
болса, онда мұндай жазықтықты фронталь проекциялаушы жазықтық деп атайды
(15б сурет). Егер берілген жазықтық профиль проекция жазықтығына
перпендикуляр болса, онда мұндай жазықтықты профиль проекциялаушы
жазықтық деп атайды (15в сурет).
Проекция осі бойымен өтетін жазықтықтырды өстік проекциялаушы
жазықтықтар деп атайды. Егер өстік проекциялаушы жазықтықтардың проекция
жазықтықтарына көлбеу бұрыштары өзара тең болса, онда биссектор жазықтығы
деп аталады.

а)
б)
в)

а) горизонталь проекциялаушы жазықтық; б)фронталь
проекциялаушы жазықтық; в) профиль проекциялаушы жазықтық.

15 сурет – Дербес жағдайдағы жазықтықтар
Денгейлік жазықтықтар проекция жазықтықтарының біреуіне параллель
орналасады, ал қалған екі проекция жазықтығына перпендикуляр (16 сурет).
Горизонталь проекция жазықтығына параллель жазықтықты горизонталь
жызықтық деп атайды (16а сурет).
Фронталь проекция жазықтығына параллель жазықтықты фронталь жызықтық
деп атайды (16б сурет).
Профиль проекция жазықтығына параллель жазықтықты профиль жызықтық деп
атайды (16в сурет).

а) б) в)

а) горизонталь жызықтық ; б) фронталь жызықтық; в)
профиль жызықтық.

16 сурет – Деңгейлік жазықтықтар

Тапсырма:
1) Берілген АВС және ЕDF жазықтықтарынын нүктесін
анықтаңыздар.А(25;45,65), В (35;70;95), С (15;50;55) және
Е(5;45;65), D(45;75;85), F(25;60;15).
2) Берілген АВС жетіспейтін фронталь проекциясын салыңыз(17
сурет).

В 2

А 2

С 2

х

А1
С1

В1

17 сурет

Сұрақтар

1. Жазықтықтар кеністікте орналасуына қарай жалпы қандай түрде
беріледі?
2. Қандай жазықтықтар денгейлік жазықтықтар деп аталады?
3. Дербес жағдайдағы деп қандай жазықтықты айтады?
4. Қандай жазықтықтар жалпы жағдайдағы жазықтықтар деп аталады?

Әдебиеттер

1 Ақпанбек Ғ. “Сызба геометрия”. – Алматы, 1998.
2 Есмуханов Ж.М., Қонақбаев Қ.Қ. Сызба геометрия. – Алматы: Мектеп,
1968.
3 Арустамов Х.А. Сборник задач по начертательной геометри. – М. :
Машгиз, 1965.
4 Четверухин Н.Ф. и др. “Начертательная геометрия” – М. : “Высшая
школа”, 1963.
5 Фролов С.А. “Начертательная геометрия”. – М. : “Машиностоение”,
1983.
6 Короев Ю.И. Начертательная геометрия. – М. : Строийиздат, 1987.

3 Модуль. Кешенді сызбаларды метрлік және позициялық есептерді
шешу жолдары

3.1 Блок. Түзулер мен жазықтықтардың іздері
Түзудің іздері деп оның проекциялар жазақтарымен қиылысу нүктелерін
айтады.Олар өздері жататын проекция жазықтықтарының атымен аталады (18
сурет). М – түзудің горизонталь ізі. N- түзудің фронталь ізі. М1 –
горизонталь іздің горизонталь проекциясы. М2 – фронталь іздің фронталь
проекциясы. N1 – фронталь іздің фронталь проекциясы. N2 – фронталь іздің
горизонталь проекциясы.
Түзу мен оның проекциясының арасындағы бұрышты,түзудің проекция
жазықтығына көлбеу бұрышы деп атайды (14 сурет). Байланыс сызықтарының
түзудің горизонталь проекциясымен қиылысуы горизонталь ізді, байланыс
сызықтарының түзудің фронталь проекциясымен қиылысуы фронталь ізді және
профиль проекциясымен қиылысуы профиль ізді береді.

Мысал:
N=N2

В2

А 2

М 2
х
N1
В1

А1

М = М1

18 сурет – АВ түзудің ізі

Жазықтықтың іздері деп оның проекциялар жазықтықтарымен қиылысу
сызықтарын айтады. Жазықтықтың горизонталь проекциялар жазықтығымен қиылысу
сызығын оның горизонталь ізі деп атайды, оны h2 деп белгілейді (20 сурет).

Мысал:

h( – жазықтың горизонталь ізі; f ( – жазықтығың фронталь
ізі; x( – жазықтық іздерінің тоғысу нүктесі.

19 сурет – Жазықтын іздері

Жазықтықтың фронталь проекциялар жазықтығымен қиылысу сызығын оның
фронталь ізі деп атайды, оны f ( деп белгілейді. .
Жазықтық горизонталь және фронталь іздері абсциссалар осінде жататын
нүктеде қиылысады. Бұл нүктені жазықтық іздерінің тоғысу нүктесі деп
атайды. ( (П2 = f (; ( (П1 = h2 (19 сурет).
Тапсырма:
1) Берілген АВ түзудің ізің салыңыз.

А 2

В 2

х

А 1

В 1

20 сурет
2) Берілген СDE үшбұрыштын іздерін салыңыз.

А 2

В 2

С 2
х

С 1

А 1
В1

21 сурет

Сұрақтар

1. Түзудің іздері деп нені айтады?
2. Түзудің горизонталь, фронталь және профиль іздері деп нені айтады?
3. Жазықтықтың іздері деп нені айтады?
4. Жазықтықтың горизонталь және фронталь іздері деп нені айтады?

Әдебиеттер

1 Ақпанбеков Ғ. Сызба геометрия. – Алматы, 1992.
2 Есмуханов Ж.М., Қонақбаев Қ.Қ. Сызба геометрия. – Алматы: Мектеп,
1968.
3 Климухин А.Г. Начертательная геометрия. – М. : Стройиздат, 1978. –
243 с .
4 Кузнецов Н.С. Начертательная геометрия. – М. : Высшая школа, 1981.
5 Арустамов Х.А. Сборник задач по начертательной геометрии. – М. :
Машгиз, 1965.
3.2 Блок. Нүктелердің өзара орналасуы
Бір проекциялаушы түзудің бойында орналасқан нүктелерді бәсекелес
нүктелер деп атайды (22сурет).
Фронталь проекциялаушы түзудің бойында орналасқан екі нүктені AB
фронталь бәсекелес нүктелер деп атайды (22 а сурет).
Горизонталь проекциялаушы түзу бойынан орналасқан екі нүктені CD
горизонталь бәсекелес нүктелер деп атайды (22б сурет).
Екі нүктенің қайсысының горизонталь немесе фронталь проекциялары
жоғары орналасса эпюрде сонысы көрінеді.

Мысал:

а)
б)

а) горизонталь бәсекелес нүктелері; б) фронталь бәсекелес нүктелер.

22 сурет - CD және AB бәсекелес нүктелер

Тапсырма:
1) Нүктелердің өзара орналасуына талдау жасаңыздар;
2) Берілген С нүктесі арқылы АВ түзуіне параллель ЕF түзуін және
онымен қиылысатын горизонталь h және фронталь f түзулерін жүргізу керек (23
сурет).

23 сурет

Сұрақтар

1. Бәсекелес нүктелер деп нені айтады?
2. Қандай нүктелерді горизонталь және фронталь бәсекелес нүктелері
дейді?

Әдебиеттер

1 Ақпанбеков Ғ. Сызба геометрия. – Ал:аты, 1992.
2 Есмуханов Ж.М., Қонақбаев Қ.Қ. Сызба геометрия. – Алматы: Мектеп,
1968.
3 Арустамов Х.А. Сборник задач по начертательной геометрии. – М. :
Машгиз, 1965 .
4 Кузнецов Н.С. Начертательная геометрия. – М. : Высшая школа, 1981.
5 Гордон В.О., Семенцов – Огиевский М.А. Курс начертательной
геометрии. – М. : “Наука”, 1968.

3.3 Блок. Жазықтықтағы түзулер мен нүктелер
Егер жазықтықтың екі нүктесі арқылы түзу жүрілген болса, онда осы
түзудің барлық нүктесі сол жазықтықта жатады.
Берілген түзудің берілген жазықтығында жатуының тағы бір белгісі бар:
жазықтықтың нүктесі арқылы өтетін және осы жазықтыққа параллель түзуге
параллель түзуде берілген жазықтықта жатады (24 сурет).

Мысал: В 2
Е 2
11
22
С 2
А 2 F2
х

F1
С1

22

А1 11
Е1 В1

24 сурет – ЕF түзуі жататын АВС үшбұрыш жазықтығы

Жазықтықта жататын және горизонталь проекциялар жазықтығына
параллель түзуді осы жазықтықтың горизонталі деп атайды (25 а сурет).
Жазықтықта жататын және фронталь проекциялар жазықтығына параллель
түзуді осы жазықтықтың фронталі деп атайды (25 б сурет).

а) б)

а) горизонталь сызығы; б) фронталь сызығы.

25 сурет – Жазықтың деңгейлік сызықтары
Жазықтықтың денгейлік сызықтарына перпендикуляр болатын және сол
жазықтықта жататын түзулерді жазықтықтың ең үлкен көлбеу сызықтары р деп
атайды (26 сурет).

26 сурет – АВС үшбұрыш жазықтықтығына ен үлкен көлбеу сызығы

Тапсырма:
1) Берілген АВС үшбұрыш жазықтығында жататын ЕF түзудің
горизонталь проекция бойынша оның фронталь проекциясын
салыңыздар (27 сурет).

В2

С2

А2

х

Е1 С1

А1
F1

В1

27 сурет
2) Берілген АВС үшбұрыш жазықтығында жататын денгейлік түзулерді
салыңыз (28 сурет).
В2

А2
С2
х
С1

А1
В1

28 сурет

Сұрақтар

1. Эпюрде қандай жағдайда түзу жазықтықта жатады?
2. Жазықтықта жататын нүктенің проекциялары қалай салынады?
3. Жазықтықтың деңгейлік түзулері деп нені айтады?
4. Жазықтықтың ең үлкен көлбеу сызығы деген не?

Әдебиеттер

1 Ақпанбеков Ғ. Сызба геометрия. – Алматы, 1992 .
2 Есмуханов Ж.М., Қонақбаев Қ.Қ. Сызба геометрия. – Алматы: Мектеп,
1968 .
3 Арустамов Х.А. Сборник задач по начертательной геометри. – М. :
Машгиз, 1965.
4 Климухин А.Г. Начертательная геометрия. – М. : Стройиздат, 1978.
5 Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии.
– М. : “Наука”, 1968.

3.4 Блок. Түзу мен жазықтықтың қиылысуы
Түзу берілген жазықтықта жатпаса, онда олардың жалғыз ортақ нүктесі
болады. Берілген түзу мен жазықтықтың ортақ екі, нүктесі болса, онда түзу
жазықтықта жатар еді, бірақ түзу берілген жазықтықта жатпайды. Олардың
ортақ нүктесі өзіндік немесе өзіндік емес болуы мүмкін. Соңғы жағдайда түзу
мен жазықтық параллель болады. Эпюрде түзу мен жазықтықтың қиылысу нүктесін
салу үшін, жазықтықтың фронталь проекциялары болатын нүктелер өрісі мен
оның горизонталь проекциялары болатын нүктелер өрісі аралығындағы тектес
сәйкестікті пайдалануға болады. Түзудін жазықтықпен қиылысу нүктесін табу
үшін, берілген түзу арқылы өтетін көмекші горизонталь проекциялаушы
жазықтық алып, жазықтықтың – өзара қиылысу сызығын анықтаймыз.
Мысал:
Жалпы жағдай орналасқан АВС жазықтығымен FE түзуінің қиылысуы сызығын
табу керек (29 сурет).
A2 B2 C2 проекциясымен қиылысуы 12 22, l жазықтығының АВС ұшбұрышымен
қиылысуы сызығының фронталь проекциясы. Проекциялық байланыс сызықтары
жүргізіліп 1121 проекциясы табылады. 11 21 пен AB-ның қиылысуынан іздеп
отырған нүктенің горизонталь проекциясы N2 тауып, түзудің көрінбейтін
бөліктері анықталады.

29 сурет – Жалпы жағдай орналасқан АВС жазықтығымен FE түзуінің
қиылысуы сызығын
Тапсырма:

1) АВ түзумен DEF үшбұрышының қиылысу нүктесін салыңыздар (30
сурет)

D2

A2
C2
F2

B2

C1
A1

B1 D1

30 сурет

Сұрақтар

1. Түзу мен жазықтықтың қиылысу нүктесі қалай анықталады?
2. Не себепте көмекші қиюшы жазықтықтарды проекциялаушы етіп таңдап
алады?

Әдебиеттер

1 Есмуханов Ж.М., Қонақбаев Қ.Қ. Сызба геометрия. – Алматы: Мектеп,
1968.
2 Ақпанбеков Ғ. Сызба геометрия. – Алматы, 1992 .
3 Арустамов Х.А. Сборник задач по начертательной геометри. –М. :
Машгиз, 1965.
4 Климухин А.Г. Начертательная геометрия. – М. : Стройиздат, 1978.
5 Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии.
– М. : “Наука”, 1968 .

3.5 Блок. Екі жазықтықтың өзара орналасуы

Кеңістікте екі жазықтық қиылысады, немесе параллель болады. Екі
жазықтық өзара параллель болуы үшін олардың біреуіне қиылысатын екі түзуі
екіншісінің сәйкес екі түзуіне параллель болулары қажет (31 а-сурет(.

Егер әр түрлі екі жазықтық ортақ нүктесі болса, олардың қиылысуы түзу
болады. Мұндай жазықтықтар қиылысушы жазықтықтар деп аталады. Екі жазықтық
түзу сызық бойымен қиылысатын болғандықтан, қиылысу сызығын салу үшін
олардың екі ортақ нүктесін тапса болды (31б-сурет).
Мысал:

а)
б)

а) өзара параллель; б) өзара қиылысушы.

31 сурет – Кеністікте жазықтықтардың өзара орналасуы:

Тапсырма:
1) АВС және СDE үшбұрыштарының қиылысу сызығын салыңыздыр (32
сурет).

32 сурет

Сұрақтар

1. Қандай жазықтықтар өзара параллель болады?
2. Қандай жазықтықтар өзара қиылысушы ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.