Функция және нүктедегі шегі: анықтамалар, біржақты шектер және негізгі теоремелер


§1 Функция. Функцияның шегі
1. 1 Негізгі түсінік
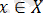
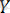
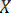 Функция ұғымы негізгі математикалық ұғымдардың бірі. Бұл ұғым екі жиынның элементтері арасындағы тәуелділікті (байланысты) орнатумен байланысты. Екі бос емес және жиындары берілсін. Әрбір
Функция ұғымы негізгі математикалық ұғымдардың бірі. Бұл ұғым екі жиынның элементтері арасындағы тәуелділікті (байланысты) орнатумен байланысты. Екі бос емес және жиындары берілсін. Әрбір
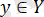 элементіне тек бір ғана элементін сәйкес қоятын
элементіне тек бір ғана элементін сәйкес қоятын
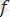 сәйкестігі функция деп аталып,
сәйкестігі функция деп аталып,
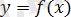 ,
,
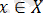 немесе
немесе
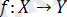 арқылы белгіленеді. Сонымен қатар,
арқылы белгіленеді. Сонымен қатар,
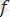 функциясы
функциясы
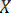 жиынын
жиынын
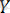 жиынына бейнелейді деп те атайды.
жиынына бейнелейді деп те атайды.
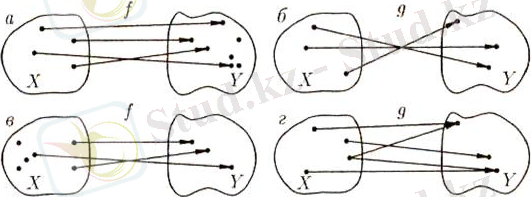
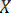 жиынын
жиынын
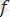 функциясының анықталу облысы деп аталып,
функциясының анықталу облысы деп аталып,
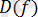 арқылы белгіленеді. Ал барлық
арқылы белгіленеді. Ал барлық
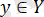 элементтерінің жиыны
элементтерінің жиыны
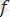 функциясының мәндер жиыны деп аталып,
функциясының мәндер жиыны деп аталып,
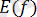 арқылы белгіленеді.
арқылы белгіленеді.
1. 2 Сандық функциялар. Функция графигі. Функцияның берілу тәсілдері
Функцияны берудің аналитикалық, кестелік, графикалық тәсілдері жиі кездеседі.
Аналитикалық тәсіл : функция бір немесе бірнеше формулалар немесе теңдеулер арқылы беріледі.
Мысалы:
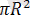
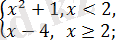
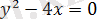 .
.
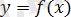 функциясын толық зерттеуге мүмкіндік беретін математикалық талдаудың әдістері қолданылғандықтан функцияның берілуінің аналитикалық тәсілі ең тиімді тәсіл болып табылады.
функциясын толық зерттеуге мүмкіндік беретін математикалық талдаудың әдістері қолданылғандықтан функцияның берілуінің аналитикалық тәсілі ең тиімді тәсіл болып табылады.
Графиктік тәсілмен берілуінің артықшылығы оның көрнектілігінде, ал кемшілігі - нақты еместігінде.
Кестелік тәсіл: функция аргумент мәндерінің және сәйкес функция мәндерінің кестесі түрінде беріледі. Мысалы, тригонометриялық функциялардың мәндерінің кестесі, логарифмдік кестелер.
1. 3 Функцияның нүктедегі шегі
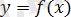 функциясы
функциясы
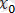 нүктесінің қандай да бір маңайында (
нүктесінің қандай да бір маңайында (
 нүктесінің өзі кірмеуі мүмкін) анықталсын.
нүктесінің өзі кірмеуі мүмкін) анықталсын.
Функция нүктедегі шегінің екі өзара эквивалентті анықтамасын тұжырымдайық.
Анықтама 1.
(«тізбектер» тілінде немесе Гейне бойынша) . Егер
 -ге жинақталатын
-ге жинақталатын
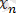 ,
,
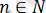 аргументінің мүмкін мәндерінің кез-келген тізбегі А санына жинақталса, А саны
аргументінің мүмкін мәндерінің кез-келген тізбегі А санына жинақталса, А саны
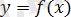 функциясының шегі деп аталады. Бұл жағдайда
функциясының шегі деп аталады. Бұл жағдайда
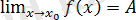 немесе
немесе
 болғанда
болғанда
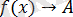 деп жазады.
деп жазады.
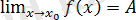 функциясы шегінің геометриялық мағынасы:
функциясы шегінің геометриялық мағынасы:
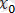 нүктесіне жеткілікті жақын барлық
нүктесіне жеткілікті жақын барлық
 нүктесі үшін функцияның сәйкес мәндері
нүктесі үшін функцияның сәйкес мәндері
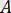 санынан аз ғана айырмашылығы болады.
санынан аз ғана айырмашылығы болады.
1. 4 Бір жақты шектер
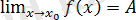 функция шегінің анықтамасы бойынша
функция шегінің анықтамасы бойынша
 нүктесі
нүктесі
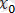 -ге кез-келген жағдайда ұмтылады:
-ге кез-келген жағдайда ұмтылады:
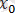 ден кіші болса да,
ден кіші болса да,
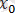 ден үлкен болса да немесе
ден үлкен болса да немесе
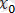 нүктесінің аймағында ауытқыса да.
нүктесінің аймағында ауытқыса да.
Кейде
 аргументінің
аргументінің
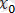 -ге жақындауының тәсілі функция шегінің мәніне айтарлықтай әсер ететін жағдайлар болады. Сондықтан, бір жақты шектер ұғымы енгізіледі.
-ге жақындауының тәсілі функция шегінің мәніне айтарлықтай әсер ететін жағдайлар болады. Сондықтан, бір жақты шектер ұғымы енгізіледі.
Егер кез-келген
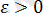 үшін
үшін
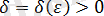 саны табылып,
саны табылып,
 болғанда
болғанда
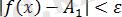 теңсіздігін орындалса,
теңсіздігін орындалса,
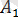 саны
саны
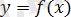 функциясының сол жақ шегі деп аталады. Сол жақ шекті
функциясының сол жақ шегі деп аталады. Сол жақ шекті
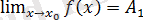 деп немесе қысқаша,
деп немесе қысқаша,
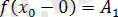 деп жазады. Осылайша, функцияның оң жақты шегі анықталып, қысқаша төмендегідей жазылады:
деп жазады. Осылайша, функцияның оң жақты шегі анықталып, қысқаша төмендегідей жазылады:
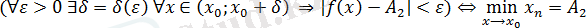
Оң жақты шекті қысқаша
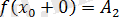 деп белгілейді. Функцияның оң жақты және сол жақты шектері
бір жақты шектер
деп аталады. Егер
деп белгілейді. Функцияның оң жақты және сол жақты шектері
бір жақты шектер
деп аталады. Егер
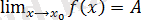 бар болса, онда екі бір жақты шектер бар болады және
бар болса, онда екі бір жақты шектер бар болады және
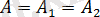 . Кері тұжырым да орынды: егер екі бір жақты шектер бар болса және олар тең болса, онда
. Кері тұжырым да орынды: егер екі бір жақты шектер бар болса және олар тең болса, онда
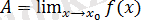 және
және
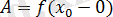 шегі бар болады. Егер
шегі бар болады. Егер
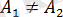 болса, онда
болса, онда
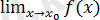 шегі жоқ.
шегі жоқ.
1. 5 Шектер туралы негізгі теоремалар
Теорема. Екі функцияның шектерінің қосындысы (айырмасы) олардың шектерінің қосындысына (айырмасына) тең:
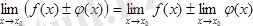 .
.
Теорема. Екі функцияның көбейтіндісінің шегі олардың шектерінің көбейтіндісіне тең:
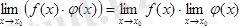 .
.
Салдар. Тұрақты көбейтіндіні шек таңбасының алдына шығаруға болады
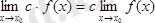 .
.
Теорема. Егер бөлшектің бөлімінің шегі 0-ден өзгеше болса, бөлшектің шегі бөлшек алымының шегінің бөлімінің шегіне бөліндісіне тең:
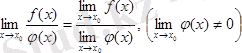 .
.
1. 6 Бірінші тамаша шек.
Көп жағдайда өрнегі тригонометриялық функциядан құралған шекті есептегенде, бірінші тамаша шек деп аталатын
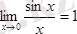 .
.
шегі қолданылады. Бұл шек былай оқылады: аргументі нөлге ұмтылғандағы синустың аргументіне қатынасының шегі бірге тең.
1. 7 Екінші тамаша шек
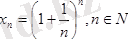 сандық тізбегінің шегі
е
-ге тең (15. 6) :
сандық тізбегінің шегі
е
-ге тең (15. 6) :
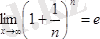 .
.
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz