Ерітінділердің жалпы сипаты туралы

Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 17 бет
Таңдаулыға:

ЖОСПАР

1 Ерітінділердің жалпы сипаты2

2 Идеал ерітінді. Рауль заңы, Коновалов заңы5

3 Идеал ерітінділердің термодинамикалық қасиеттері12

4 Идеал ерітінділердің қайнау және балқу температуралары16

5 Қатты заттың ерігіштігі. Шредер теңдеуі19

1 Ерітінділердің жалпы сипаты

Ерітінді деп екі немесе бірнеше компоненттен тұратын гомогенді системаларды айтады. Әдетте ерітінділердің тығыздығы, қайнау және қату температурасы, тұтқырлығы сияқты қасиеттері өзгеріп отырады. Ерітінділерді жай механикалық қоспа деп те, химиялық қосылыс деп те қарастыруға болады. Ерітіндінің механикалық қоспадан басты айырмашылығы ондағы әрбір микроскопиялық (өте кіші, ұсақ) бөлшектерді химиялық құрамы мен физикалық қасиеттерінің көлемде бірдей болуында. Ал химиялық қосылыстардан негізгі өзгешелігі оның құрамының еритін зат көп еріткіштің мөлшеріне тәуелділігінде және еселік қатынас заңына бағынбауында. Мысалы, ас тұзы суда тек белгілі мөлшерде ғана ериді. Айталық, 20°С (293К) -та алынған 100 мл суда ас тұзының 36, 8 грамы ғана ериді де, одан әрі оның мөлшерін қанша көбейтсек те ол ерімейді. Бұл қалыпты жағдайда кездесетін құбылыс. Ерітіндінің химиялық қосылыстан тағы бір өзгешелігі - химиялық байланыс табиғатында. Егер химиялық қосылыстар негізінен ионды, ковалентті байланыстармен сипатталса, ерітіндідегі байланыс, газдарда кездесетін аса әлсіз ван-дер-ваальстік, ал кейбір жағдайларда қосымша сутектік байланыстармен түсіндіріледі.

Жай қоспалардағы заттар өзара ешбір байланыссыз-ақ араласса, ерітіндідегі еріткіш пен еритін заттар арасында әлсіз болса да химиялық байланыс болады. Мысалы, бірдей өлшемдегі кұм мен ағаш немесе темір үгіндісін араластырса, қоспа пайда болады және оларды бір-бірінен бөлуге болады. Ал, ас тұзын немесе қантты суда ерітсе, олар оңайлықпен әуелгі жеке заттарға бөлінбейді.

Көбінесе, екі зат, бір-бірінде ерігенде, олардың арасында өзінің агрегаттық күйін өзгертпейтін немесе ерітінді құрамындағы мөлшері басым болатын бөлікті еріткіш дейді. Демек, «еріткіш», «еритін зат» ұғымдары салыстырмалы екенін ескеру керек. Мысалы, спирт пен судың тең бөлігін бір-бірінде ерітсе, олардың қайсысының еритін зат, қайсысының еріткіш екенін ажырату қиын, өйткені екеуі де сұйық және бір-бірінде ерігіштіктері бірдей. Мұндайда ерітінді құрамындағы компоненттер туралы айтқан дұрыс. Сондықтан компоненттердің агрегаттық күйін ескеріп, ерітінділерді үш топқа бөлуге болады: газдың газдардағы ерітіндісі (газ қоспасы) ; сұйық ерітінділер; қатты ерітінділер. Газ ерітінділеріне ауа, ал қатты ерітінділерге түрлі металдардың қорытпалары мысал болады. Ал, сұйық ерітінділер газдардың сұйықтағы ерітінділері; сұйықтың сұйықтағы ерітінділері, қатты заттардың сұйықтағы ерітінділері болып бөлінеді.

Еріткіші су болатын ерітінділер табиғатта кең тараған. Жер қыртысындағы, өсімдіктер мен тірі организмдердегі процестер сусыз жүрмейді. Осыдан ерітінді дегеніміз жай ғана құбылыс емес, ол өте күрделі физикалық және химиялық қасиеттері бар күрделі құбылыс екенін көреміз.

Еру процестері кейде жылу бөліну арқылы жүрсе, енді бірде жылу сіңіру арқылы да жүреді, яғни зат қыздырғанда ғана ериді. Сондай-ақ, кей заттарды еріткенде ерітіндінің көлемі кемуі немесе артуы мүмкін. Мысалы, күкірт қышқылын не натрий гидроксидін суда еріткенде едәуір жылу бөлінеді. Бұл еріген зат пен еріткіш арасында химиялық реакцияның жүргендігін көрсетеді. Бұл процесті сольватация, ал пайда болған қосылысты сольват дейді. Зат суда еритін болса, процесс, гидратация, қосылыс гидрат делінеді.

Ерітінді жайлы ілім өз алдына жеке бөлім болып, жалпы табиғаттану ғылымынан бөліне бастағаннан оның табиғатына қатарынан екі көзқарас қалыптаса бастайды. Олардың бірін - ерітінділердің физикалық, ал екіншісін - химиялық теориясы дейді. Ерітінділердің физикалық теориясы XIX ғасырдың екінші жартысында қалыптасты. Ол теорияның негізін салушылар С. Аррениус пен Я. Вант-Гофф болды. Бұл теория еру процесі жай физикалық қоспа ретінде, еритін заттардың ұсақ бөлшектері еріткіш көлемінде біркелкі таралған, олардың араларында ешбір әрекет болмайтын орта сияқты ұғымда қарастырылады. Олай болса, бұл теория еритін зат пен еріткіш араларында ешбір химиялық әрекет жүрмейді деген пікірді теріске шығармайды. Жалпы физикалық теория ерітінділердің қайнау температураларының жоғарылауы, қату температураларының төмендеуі, будың қысымы, осмостық қысым сияқты қасиеттеріне сүйенді. Бұл шамалар ерітінділердің концентрациясына тәуелді де, еріген заттың табиғатына тәуелсіз. Сондықтан да бұл теория бойынша ерітінділер еріген заттардың күйі газ күйіндегі ерітінділер секілді болып келетін молекулалардың бірыңғай қоспасы іспеттес.

Ерітінділердің химиялық теориясының негізін қалаушы Д. И. Менделеев болды. Бертін келе, бұл теорияға И. А. Каблуков, Н. С. Курнаков сияқты әйгілі совет ғалымдары елеулі үлес қосып, оны жаңа деңгейге көтерді. Бұл теорияны бірінші тұжырымдаған Д. И. Менделеев күкірт қышқылының, этил спиртінің және басқа да қосылыстардың судағы ерітінділерін нақты, жан-жақты зерттеді. Мұның нәтижесінде ол, ерітіндідегі компоненттер арасында, яғни еріген зат пен еріткіш арасында химиялық әрекеттер жүреді деген қорытынды шығарды. Мысалы, Менделеев күкірт қышқылының ерітінділерінде бірнеше гидраттардың түзілетінін анықтады. Ол сондай-ак, еріткіш пен еритін зат молекулаларының арасындағы байланыс негізінен сутектік байланыс арқылы немесе ондағы қосылыстар құрамына енетін полюсті молекулалар араларындағы өзара электростатистикалық әрекеттесу салдарынан болатынын анықтады.

2 Идеал ерітінді. Рауль заңы, Коновалов заңы

Идеал ерітінді. Рауль заңы. Кез келген затты еріткенде еріткіш буының қысымы төмендейтінін көптеген тәжірибе көрсетті. Осы негізде ерітінді құрамы мен бу қысымының төмендеуі араларындағы байланысты Ф. Рауль ашқан. Оған дейінгі оқымыстылар тек қышқылдар мен негіздердің судағы ерітінділерін ғана зерттеп, онда кездесетін диссоциация сияқты, әлі табиғаты толық айқын емес құбылыстарға келгенде, оны түсіндіре алмады. 1882 жылы Рауль отыздан астам органикалық қосылыстың судағы әр түрлі концентрациялы ерітінділерін зерттеп, олардың қату температураларын анықтайды. Қандай қосылыс болмасын, олардың бір молін литр еріткішке (суда) еріткенде, осы ерітінділердің бәрінің қатаю температуралары бір шамаға, дәлірек айтқанда 1, 85°С-қа төмендейтінін байқайды. Бұл заңдылық еріген заттың табиғатына тәуелсіз болды. Ол судың орнына бензолды алып, онда бір мольден бірнеше органикалық қосылыстарды ерітеді. Мұнда да құрылысы мен табиғатына тәуелсіз бірдей көлемдегі бензолда бірдей мольдегі органикалық қосылыстарды еріткенде ерітінділердің қату температуралары бір шамаға ғана төмендеген. Мысалы, Рауль тәжірибесіндегі ерітінділердің бәрі де 5, 2°С-та қатқан, ал таза бензол 5, 5°С-та кристалданады. Сосын, Рауль 1886 жылы қату температурасынан кейін сусыз ерітінділердің бу қысымын анықтауға ауысады. Бұл, 1887 жылғы ғылыми баспада жарияланған тәжірибе нәтижесінде табылған заңға әкеледі. Ал, егер Р° _А - берілген температурадағы будың таза еріткіш үстіндегі (бетіндегі) қысымы десек, ал Р _А - осы температурадағы еріткіш буының ерітінді бетіндегі қысымы. Онда Р° _А - Р _А айырмасы бу қысымының төмендеуіне тең.

(Р° _А - Р _А ) / Р° _А - қатынасы берілген ерітінді үшін бу қысымының салыстырмалы төмендеуі. Рауль заңының тұжырымдалуына орай, ерітінді бетіндегі еріткіш қысымының салыстырмалы төмендеуі, сұйықта еріген заттың мольдік үлесіне тең:

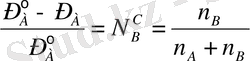(1)

Бу қысымының салыстырмалы төмендеуі берілген ерітіндідегі еріген және оны еріткен заттардың табиғаты мен температурасына тәуелсіз. Еріген кездегі жылуы нөлге тең, яғни жылу бөлінбейтін және көлемі еріген және ерітетін компоненттер көлемдерінің қосындысына тең болатын ерітінділер үшін Рауль заңының дұрыстығы байқалады.

Кез келген температура мен концентрацияларда Рауль заңына бағынатын ерітінділерді идеал ерітінділер дейді. Идеал ерітіндіден басқалардың бәрі де Рауль заңынан шамалы болса да ауытқиды. Алайда, бұл ауытқу ерітінді концентрациясы төмендеген сайын азаяды және ерітіндіні шексіз сұйылтқан кезде (1) теңдеудің екі жағынан да 1-ді азайтқандағы қатынас тұрақты температурада әркез орындалады:

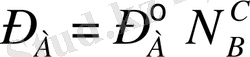(2)

Ерітінді бетіндегі еріткіш буының қысымы ерітіндідегі еріткіштің мольдік үлесіне тура пропорционалды және ондағы пропорционалдық коэффициенті берілген температурадағы қаныққан будың таза еріткіш бетіндегі қысымы болады.

Ерітінді теориясы үшін идеал ерітінділердің мәні өзгеше. Өйткені оны идеал газдармен салыстырғанда идеал ерітінділерде молекулааралық әрекет болады.

Сұйық заттардың бәрінде де молекулааралық әрекет бар. Системалары бір түрдегі молекулалардың араларындағы әрекет, осы система құрамына енетін басқа түрдегі молекулалардың араларындағы әрекет бірдей болса, ондай ерітінділерді идеал ерітінділер дейді. Бұл пікірді математика тілімен өрнектесек Е _АА =Е _АВ =Е _ВВ . Мұндағы Е - әртүрлі зат молекулаларының әрекеттесу энергиясы, А және В - молекула түрлері. Химиялық және физи-калық қасиеттері ұқсас заттарды араластырғанда олар бір-бірінде еритін болса, идеал ерітінді пайда болады.

Идеал ерітінділер үшін. Т=const жағдайында келесі шарттар орындалуы керек:

1. U = Σn _і U _і - идеал ерітінділердің ішкі энергиясы, ол құрамына енетін компоненттердің ішкі энергияларының қосындысына тең.

2. V = Σn _і V _і - идеал ерітіндінің көлемі, сол ерітінді құрамына енетін жекеленген компоненттер көлемдерінің қосындысына тең.

3. S = Σn _і S + ∆ _mix S - идеал ерітінді энтропиясы онын, құрамына енетін компоненттердің энтропия қосындысы мен араластыру (еріту) энтропиясының қосындысына тең. Мұнда да араластыру (еріту) энтропиясы идеал газдардағыдай (∆ _mix S) таңбаланады.

Рауль заңын пайдаланып, идеал ерітінді бетіндегі қысымының ерітінді құрамына тәуелділігін көрсетуге болады. Егер ерітінді құрамына енетін екі компонент үшін Рауль заңы орындалса:

(2а)

және (2б)

N _A + N _B = 1; N _A = 1 - N _B (2в)

онда будың жалпы қысымы

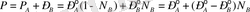(2)

яғни жалпы қысым ерітінді құрамынан түзу сызықты тәуелділікте болады.

Бұл тәуелділік 14-суретте көрсетілген. Онда бензол мен толуолдың бір-біріндегі ерітінділері белгілі температура аралырында алынды. Бензол мен толуолдың физикалық, химиялық қасиеттері және кеңістіктегі құрылымы ұқсас. Сондықтан олар белгілі бір температура аралығында 0≤N≤1 шарты орындалғанда Рауль заңына бағынады (N - компонент құрамы, ол мольдік, көлемдік үлеспен, процентпен беріледі) .

(2а) және (2б) теңдеулерін өзара бөлсек, төмендегідей қатынас шығады:

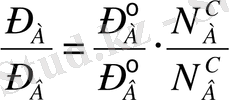(2а)

Бұл теңдеудің сол жағындағы өрнектің алымын да, бөлімін де жалпы қысымға (Р = Р _А +Р _В ) бөлсек:

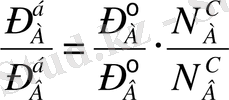(2б)

мұндағы «б»- бу -«с»- сұйық күйдегі фазаларды көрсетеді. Мұнан идеал системалардағы бу мен оған тепе-теңдіктегі сұйық құрамы бірдей болмайтыны байқалады. Олар өзара бірдей болуы үшін, таза компоненттердің бетіндегі қаныққан будың қысымдары да өзара тең болуы керек: Р° _А =Р° _В . Бұл жағдай орындалмаса, ерітінді бетіндегі будың құрамында, жеңілдеу буланатын (тезірек, ертерек қайнайтын) компоненттің буы молырақ болады,

яғни 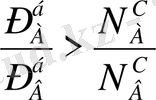, егер .

Бұл Коноваловтың (1881) бірінші заңы деп аталады да, былайша тұжырымдалады; қаныққан буды теңдіктегі ерітіндімен салыстырғанда, системаға қосылған компонент сол ерітіндінің жалпы қысымын арттыратын немесе қайнау температурасын төмендететін болса, онда қаныққан бу құрамындағы компонент ерітінді құрамындагыдан мол болады. Бұл заңды басқаша былай да тұжырымдауға болады:

а) берілген компоненттің мөлшерін сұйық фазада салыстырмалы ғана арттыру оның будағы салыстырмалы мөлшерінің молаюына әкеледі;

б) еселенген системадағы буды онымен теңдікте болатын сұйықпен салыстырғанда, системаға қосқанда жалпы қысымды көбейтетін немесе қай-нау температурасын сол қысымда төмендететін компонент буына салыстырмалы түрде молырақ болады.

Коноваловтың бірінші заңын тек идеал ерітінділерге ғана емес, Рауль заңына бағынбайтын ерітінділер үшін де қолдануға болады.

Жалпы қысымның сұйықтық құрамына (1-қисық) және будың құрамына (2-қисық) тәуелділігі 15-суретте келтірілген. Онда екі компонент бар. Олардың бірі - бензол (А компоненті) . Таза бензол 80°С-та қайнайды. Екіншісі - толуол не метилбензол (В компоненті) . Таза толуол 110°С-та қайнайды. Олардың физикалық, химиялық қасиеттері және структуралық құрылымы ұқсас. Диаграммадағы 1-қисықтың үстінде сұйық, 2-қисықтың астында бу орналасқан. Әрине, мұнда дп теңдік жағдайы болу керек. Со-нымен, диаграммадағы Р° _А және Р° _В нүктелерінде бу мен сұйықтың құрамы бірдей. Бензолдың қайнау температурасы толуолдікінен төмен болғандықтан, оның бу қисығының әрбір нүктесі 1-сызықтан солға қарай ығысады. 1 және 2-қисықтың ортасында сұйық пен бу өзара тепе-теңдік жағдайында болады. Сұйық пен бу сызықтарының араларына жүргізілген изобара сызықтарын нодтар дейді. Нодтардың с және d, с' және d' сияқты ұштары тепе-теңдікте болатын бу және сұйық фазалардың құрамын көрсетеді. Сол сияқты, диаграмма тұрақты температурада жасалғандықтан, ондағы әрбір нүкте система күйін толық сипаттайды. Мысалы, диаграммадағы m нүктесі системаның N _m құрамындағы бір фазалы сұйық ерітіндісіне сәйкес екенін көрсетеді. Мұндай нүктелерді фигуративті нүкте дейді.

Егер қысымды төмендетсе фигуративті m нүктесі төмендейді де с нүктесінде булана бастайды және осы кезде система екі фазалы болады. Алғашқы пайда болған будың құрамы N _d . Қысымды онан әрі төмендеткенде фигуративті нүкте 1-қисық бойымен төмендеп, с' нүктесінде тоқтады десек, осы күйдегі система кұрамы с'd' нүктелерінің абсцисса арқылы анықталатын сұйық пен бу тепе-теңдігін көретеді. Сосын қысымды тағы да төмендетсе, фигуративті нүкте 2-қисықтары с"-ге жетеді. Мұндайда барлық сұйық буға айналады және қысымды онан әрі төмендетсе, енді ондағы қысымның өзі N _m құрамдағы бу қысымына теңеледі. Бұл қарастырылған процесті изотермиялық айдау дейді.

Көптеген сұйықты не олардың қоспаларын тұрақты қысымда (мысалы р=1 атм. ) айдаған қолайлы. Ол үшін 16-суреттегі диаграмманы талдайық. Мұнда да А және В компоненттерін сәйкес түрде бензол мен толуол деп аламыз. Әдеттегіше абсцисса осіне компоненттер құрамын, ал ординатаға температура мәнін жазамыз. 1-қисық сұйықтың, ал 2-қисық будың құрамын көрсетіп, оларды шектейді. Мұндай диаграмманы алу үшін әуелі таза күйіндегі екі компоненттің қайнау температурасын табамыз. Сосын осы екеуінің әр түрлі Құрамдық қатынастағы қайнау температураларын оларға сәйкес және тепе-теңдік жағдайындағы будың да құрамын анықтаймыз. Бірінші анықталған температура мен құрам арқылы 1-қисықты, сосын екінші табылған бу құрамына орай 2-қисықты сызады. Кейде осы қисықтарды сұйық және бу қисығы дейді. Мұндай диаграммада сұйық төменде, бірінші немесе бу қисығының үстінде орналасады. Фигуративті нүктелер осы екі қисық аралығына орналасады және ол тепе-теңдікте болатын сұйық пен бу тәрізді екі фазадан тұратын гетерогенді системаны сипаттайды.

3 Идеал ерітінділердің термодинамикалық қасиеттері

Ерітіндідегі і компоненті өзінің буымен тепе-теңдікте болғанда ерітіндідегі және будағы химиялық потенциалдары бір-біріне тең:

μі = μ'і,

μі - i компоненттің ерітіндідегі химиялық потенциалы, μ'і - оның будағы химиялық потенциалы.

Егер бу идеал газдардың заңына бағынатын болса

dμ'і = dμ і = RТd\nРі, (ХІІ. 34)

Осыдан компоненттердің парциалды қысымдары мен олардың химиялық потенциалдарының арасындағы байланысты табуға болады:

dlnР ₁ = dμ ₁ / RТ dlnР ₂ = dμ ₂ / RТ (ХІІ. 35)

Бұнда Р ₁ - еріткіштің ерітінді бетіндегі парциалды бу қысымы, Р ₂ - ерітілген заттың ерітіндідегі парциалды, бу қысымы.

(XII. 34) және (ХII. 35) -теңдеуді интегралдасақ,

μi = μ ⁰ _i + RТlnP _i , (ХІІ. 36)

μ ⁰ _i - таза і-компонентінің химиялық потенциалы. Ерітінді идеал болған жағдайда ол Рауль заңына бағынады, сондықтан (ХІІ. 36) -теңдеуді төмендегідей жазуға болады:

μi = μ ⁰ _i + RТlnх _i (ХІІ. 37)

Бұл жерде Рі - і-затының парциалды қысымы, оның мәнін Рауль заңының теңдеуінен Рі = P ⁰ _i х _i алып келіп қойдық. (ХІІ. 36) -теңдеу мен (ХІІ. 37) -теңдеудегі μ ⁰ _i бірдей, себебі ол таза еріткіштің химиялық потенциалы. Оның буы идеал газдар заңдарына бағынады, ал қарастырып тұрған ерітінділер де идеал ерітінділер.

∆μ = μі - μ ⁰ _i і-затының таза күйден ертіндіге көшкендегі химиялық потенциалының өзгерісі. Ол ∆μ=μі(Р) -μ ⁰ _i =μ ⁰ _i +RTlnx _i -μ ⁰ _i =RTlnx _i .

Бинарлы ерітіндінің компоненттерінің моль сандары n ₁ және n ₂ болса химиялық потенциалдың өзгерісі Гиббс энергиясының өзгерісіне тең және төмендегідей жазылады:

∆G=n ₁ μ ⁰ ₁ +n ₁ RТlnх ₁ +n ₂ μ ⁰ ₂ +n ₂ RТlnх ₂ -n ₁ μ ⁰ ₁ -n ₂ μ ⁰ ₂ =

=n ₁ RТlnх ₁ +n ₂ RТlnх ₂ (ХІІ. 38)

Гиббс энергиясы өзгерісінің ерітіндінің 1 моліне тиісті мөлшерін тапсақ

∆G/( n ₁ +n ₂ ) = n ₁ /( n ₁ +n ₂ ) RТlnх ₁ +[n ₂ / (n ₁ +n ₂ ) ] RТlnх ₂

Осыдан

∆G=∆μ=х ₁ RTlnх ₁ +х ₂ RТlnх ₂ (ХІІ. 39)

∆G - ерітінді түзілу энергиясы. Мольдік үлестердің қосындысы бірге тең (х ₁ +х ₂ =1), онда х ₁ <1 және x ₂ <1, олай болса ерітінді түзілгенде жүйенің химиялық потенциалы мен Гиббс энергиясы азаяды, . яғни ерітінді түзілу процесі өздігінен өтетін процесс.

Идеал ерітіндінің түзілу энтальпиясын табу үшін (ХІІ. 39) -теңдеуді түрлендірейік:

∆G/Т=х ₁ Rlnх ₁ +х ₂ Rlnх ₂ (ХІІ. 40)

Бұл теңдіктің оң жағындағы мүшелер температураға тәуелсіз, ал сол жағындағы мүшенің температура бойынша туындысы нольге тең.

Гиббс-Гельмгольц теңдеуі бойынша

∂(∆G/Т) /∂Т=-∆Н/Т ²

Бұл теңдеуді еру процесіне қолданып, және оны (ХІІ. 40) -теңдеумен салыстырсақ идеал ерітінді түзілуінің энтальпиясы нольге тең болатынын көреміз.

∆Н _epim =0 (ХІІ. 41)

демек, компоненттер бір-бірімен араласып идеал ерітінді түзгенде энтальпия өзгермейді, яғни жылу бөлініп не сіңірілмейді.

Жылу сыйымдылық ∆С _Р процесс кезіндегі энтальпияның температура бойынша туындысы:

(∂∆Н/∂Т) _Р =∆С _Р

Олай болса (ХІІ. 41) -теңдеу бойынша

∆С _{Р, epim} =0. (ХІІ. 42)

Идеал ерітінділер түзілгенде жүйенің көлемі өзгермейді. Тұрақты температурада (ХII. 40) -теңдеудің оң жағы қысымға тәуелсіз, сондықтан

(∂∆G _epim /∂P) т=0

ал (∂G/∂P) т=V, осыдан V _epim = 0 (ХІІ. 43)

Бізге белгілі Н≡U+РV немесе U≡Н-РV. Осыдан

∆U _epim =∆H _epim - P∆V _epim = 0 (ХІІ. 44)

демек, идеал ерітіндінің түзілуі ішкі энергияның тұрақты жағдайында өтеді.

Көлемнің термиялық ұлгаюы және басқа да эффектілердің жоқтығы идеал ерітінділердің энтальпиясы, жылу сыйымдылығы, көлемі және ішкі энергиясы сияқты қасиеттері аддитивтік қасиеті екендігін, яғни жалпы ерітінді қасиеті таза компоненттердің қасиеттерінің қосындысына тең болатындығын көрсетеді:

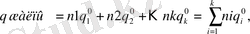
k - компонештердің жалпы саны; qжалпы днп Нжалпы, Сржалпы, Vжалпы, Uжалпы алынады.

Идеал ерітіндідегі компоненттердің энтропиясын табу үшін (ХII. 37) -теңдеуді температура бойынша дифференциалдасақ:

(∂μ/∂Т) р=(∂μ ^о і /∂Т) +Rlnхі

Осыдан

Sі=S ^о і-Rlnхі (ХІІ. 45)

Мұнда Sі - ерітіндідегі кез келген i-компонентінің энтропиясы, S ^о і - бұл компоненттің таза күйіндегі энтропиясы. Ерітінді түзілгендегі энтропияның өзгерісін табу үшін (ХІІ. 39) -теңдеуді дифференциалдаймыз:

(∂∆G _epim /∂Т) р=x ₁ Rlnx ₁ + x ₂ Rlnx ₂

Осыдан

∆S _epim =-х ₁ Rlnx ₁ - х ₂ Rlnx ₂ (ХII. 46)

Бұл теңдеудің оң жағыңдағы х ₁ <1 және х ₂ <1, себебі олардың қосындысы бірге тең (х ₁ +х ₂ =1) . Олай болса ∆S _epim >0, яғни идеал ерітінді түзілу процесі өздігінен өтетін процесс. Сонымен идеал ерітінді түзілгенде жүйенің Гиббс энергиясы азайып, энтропиясы өседі, ал энтальпиясы (∆Н=0), ішкі энергиясы (∆U=0), жылу сыйымдылығы (∆Ср=0) және көлемі (∆V=0) өзгермейді. Идеал ерітінділердің заңына кейбір органикалық заттардың қоспалары (бензол-толуол), изотоптардың, изомерлердің қоспалары бағынады.

4 Идеал ерітінділердің қайнау және балқу температуралары

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.