МОДЕЛДЕУ ЖӘНЕ КОМПЬЮТЕР ГРАФИКАСЫ

МАЗМҰНЫ

КІРІСПЕ

Қазіргі кездегі ғалым мен білікті маман қандай да бір мәселені шешу үшін қажетті ақпаратты дұрыс өңдеуді - іздеуді, таңдауды, талдауды және оны қолдануды жетік меңгеруі керек. Бүгінде табиғат пен қоғамдық ғылымдардың барлығында дерлік зерттеу жұмыстары моделдер көмегімен жүргізіледі. Компьютер көмегімен алуан түрлі процестердің моделдерін жасақтауға, олармен сансыз эксперименттер орындау арқылы ғылыми талдау, сараптау және зерттеу жұмыстарын жүргізуге болатыны баршаға мәлім. Олай болса, білім беру ісінде жаңа компьютерлік технологияларды, оның ішінде компьютерлік моделдеуді толық үйреніп, оқу үдерісінде үнемі қолданып отыру бүгінгі күннің талабы.

Компьютерлік моделдеу арқылы объектінің немесе құбылыстың нақты немесе ойдан шығарылған параметрлерін, қасиеттері мен заңдылықтарын тауып, оны экранда көрнекі бейнелеуге мүмкіндік бар. Бұл ғылым мен білімге өте қажетті мәселенің бірі. Компьютерлік моделдеу арқылы ғана көптеген физикалық, химиялық және т. б. құбылыстарды толық зерттеп тануға болады. Көрнекі компьютерлік модельдерді оқу процесінде ұтымды пайдалану арқылы білім сапасын арттыруға болатынына да күмән жоқ. Жалпы физика курсында есептер шығару кезінде, көбінесе дайын формулаларды пайдаланып, нәтижелерді параметрлердің бір-екі мәні үшін ғана есептеп тауып жүрміз. Онда да, есептеу дәлдігіне көңіл бөлмей, көбінесе жай физикалық құбылыстарды (кинематикада, қозғалыс - бір қалыпты үдемелі, динамикада, масса мен күш - тұрақты, электр тізбектері - аз тармақталған, ортамен жылу алмасу - ескерілмеген деп алып және т. с. с. ) ғана сипаттайтын формулаларды пайдалып келеміз. Жұмыстың мақсаты - жалпы физика курсынан алынған білімдерді пайдаланып компьютер көмегімен кейбір қарапайым электромагниттік құбылыстарды моделдеу арқылы тәжрибелік, эксперименттік және зерттеу жұмыстарын жүргізу.

Жұмыста Turbo Pascal 7. 0 тілінің графикалық мүмкіндіктері мен кейбір сандық әдістерді қолдану арқылы, жалпы физика курсының электр мен магнитизм бөлімдерінде кездесетін біршама күрделі 14 есепті шығарудың Паскаль тіліндегі толық программалары ұсынылған. Әрбір есепке қажет деп есептелген қысқаша теориялық түсініктемелер берілген.

Диплом жұмысы кіріспеден және 3 тараудан тұрады.

«Моделдеу және компьютер графикасы» тарауында моделдің түрлері, моделдеу кезеңдері мен компьютермен моделдеудің негізгі принциптері сөз болып, Turbo Pascal 7. 0 графикасы мен мүмкіндіктері айтылған.

«Моделдеуге қажетті сандық әдістер» тарауында физиканың электр және магнитизм бөлімдерінде кездесетін есептерді компьютермен моделдеуге пайдаланылатын кейбір сандық әдістер келтірілген.

«Электромагниттік құбылыстарды моделдеу» тарауында физиканың электр және магнитизм бөлімдерінен алынған 14 есепті компьютермен моделдеу іске асырылып, Паскаль тіліндегі толық программалары келтірілген.

Құрылған программалар көмегімен параметрлерді керегінше өзгерте отырып қарастырылып отырылған физикалық үдерістерді жан-жақты бақылауға, зерттеуге, яғни олармен әртүрлі физикалық эксперименттер жасауға болады деп есептейміз.

Тақырыптың көкейтестілігі: Жалпы физикадағы көптеген құбылыс-тарды зерттеу мен есептерді шығаруда компьютерлік модельдеуді пайдалану оқу процесінде студенттер мен оқушылардың физика пәніне ынтасын арттырып қана қоймайды, олардың ғылыми танымын және өзбетімен зерттеу қабілеттерін де жандандырады. Ал модельдерді жасақтау, сынау және дұрыс нәтижелер алу орындаушыдан тапқырлықты, логикалық дәл пайымдауды және программалық сауаттылықты талап етеді. Бұл оқушының жалпы дүние танымын кеңейтіп, оны іскерлікке, шыдамдылыққа, ұстамдылыққа, ізденімпаздыққа және жауапкершілікке тәрбиелейді.

Жұмыстың мақсаты: жалпы физика курсынан алынған білімдерді пайдаланып компьютер көмегімен кейбір қарапайым электромагниттік құбылыстарды моделдеу арқылы тәжрибелік, эксперименттік және зерттеу жұмыстарын жүргізу.

Зерттеудің нысаны: Электромагниттік құбылыстар мен есептерді компьютермен модельдеу.

Пәні: Программалау.

Болжам: Компьютермен модельдеуді пайдалану арқылы пайдаланушыға физикалық құбылыстарды толығырақ түсінуге қол жеткізеді.

Зерттеу міндеттері:

1. Сандық әдістерді пайдалана білу;

2. Паскаль графикасын толық түсіну және оларлы программауда орынды пайдалануды үйрену;

3. Физикалық заңдылықтарды жете меңгеру. Физикалық есептерді таңдай білу. Оларды моделдеуде программалау әдістерін меңгеру. Программаларды жетілдіре білу.

Зерттеудің практикалық маңыздылығы : Оқушының физикалық құбылыстарды жете түсініп, электромагнитизм бөліміндегі кейбір қиын есептерді көп қиналмай шығаруына және компьютер көмегімен әртүрлі эксперименттер жүргізуіне мүмкіндік туғызады.

I ТАРАУ. МОДЕЛДЕУ ЖӘНЕ КОМПЬЮТЕР ГРАФИКАСЫ

1. 1 Моделдің түрлері және моделдеу кезеңдері

Шындығында, нақты объектілер мен оған қатысты құбылыстар көп қырлы және күрделі болып келеді, сондықтан олардың барлық қырларын бірдей ескеріп тану және зерттеу кейде мүмкін болмайды. Сондай жағдайда, зерттеудің ең жақсы әдісі нақтылықтың бір немесе бірнеше қырын ғана бейнелейтін моделді құру және оны пайдалану болып табылады. Ғылымның көп ғасырлық тәжірибесі бұл амалдың пәрменділігін іс жүзінде дәлелдеп отыр. Модель - объектіні немесе құбылысты жобалап (нобайлап) сипаттау. Ол объектінің немесе құбылыстың құрылымын, негізгі қасиеттерін, даму және қоршаған ортамен өзара қарым-қатынас заңдарын анықтау, басқару әдістерінің ең тиімділерін айқындау, іс - әрекеттерін болжау үшін керек. Бір объектінің бірнеше моделі болуы, немесе түрлі объектілер бір модель арқылы сипатталуы мүмкін. Қажет моделді таңдау зерттеудің мақсатына байланысты болуы тиіс.

Моделдің мынадай түрлері болады:

• Математикалық модель. Мұндай моделдер объектінің (құбылыстың) елеулі ерекшеліктерін көрсететін теңдеулер және функциялар негізінде құрылады.
• Натуралдық модель. Бұларға техникалық моделдер, мысалы, автомобиль мен ұшақтың моделдері жатады.
• Ақпараттық-логикалық модель. Зерттеудегі объект (құбылыс) туралы қажетті ақпараттың бәрін қамтитын шамалар жиынтығы ақпараттық модель деп аталады. Мысал ретінде ақпарат ұсынудың әмбебап құралы- кестені, блок-схеманы атауға болады.
• Графикалық модель. Бұған фотосуреттер, график, суреттер, схемалар, сызбалар мысал бола алады.
• Сөзбен сипаттау. Бұл объектінің негізгі құрамдық бөліктерін, аса маңызды белгілері мен қасиеттерін сөзбен санап шығу. Мұндай моделдердің мысалы ретінде алгоритмді, жол жүру ережелерін және т. б. атауға болады.

Модель жасақтауды төрт кезеңге бөлуге болады:

Бірінші кезең - модель жасаудың мақсаттарын анықтау.

Оның міндеті - нақты объектінің қалай жасалғандығын, оның құрылымы, негізгі қасиеттері, даму және қоршаған ортамен өзара қарым-қатынас заңдарының қандай екендігін түсіну. Объектіні басқаруды үйрену және қойылған мақсаттары мен критерийлері бойынша оны басқарудың ең тиімді әдістерін анықтау. Объектіге ықпал жасаудың тікелей және жанама салдарын болжай білу.

Екінші кезең - алғашқы үрдістің (объектінің) нобайлануы.

Бұл кезеңде ақпараттың нақты объектіден оқшаулануы жүреді, маңызды ақпарат бекітіліп, елеусізі алынып тасталады. Объектінің іс- әрекетіне немесе үрдістің барысына бағынышты шамалардың (кірістік шамалар) және модель жасау нәтижесінде алынуға тиісті шамалардың (шығыстық шамалар) тізімі жасалады. Бір есеп үшін елеусіз ақпарат басқасы үшін маңызды болуы мүмкін және одан айырылу есептің дұрыс шешілмеуіне әкелетінін немесе қажет шешімді алуға мүмкіндік бермейтінін ескеру маңызды. Елеусіз ақпараттың тіркелуі қосалқы қиындықтар әкелуі, шешімге жетелейтін жолда кедергілер жасайуы мүмкін.

Үшінші кезең - сипаттаманы іздеу.

Бұл кезеңде моделденіп жатқан объекті туралы ақпарат құрылымданып, компьютерде өңделуге дайындалады. Моделдің абстрактілі сипаттау тұжырымдамасынан нақты толыққанды тұжырымдамасына өту қажет.

Төртінші кезең - ЭЕМ-ге арналған программаны құрастыру. Бұл шығармашылық жұмыс және қиын атқарылатын үрдіс.

Қазіргі кезде құрылымдық және объектіге бағдарланған программалаудың амалдары кеңінен таралған. Программалау тілін таңдау әдетте программистің тәжірибесіне, стандарттық бағыныңқы программалар және ашық кітапханалар болуына байланысты. Кейбір жағдайларда есептеулерді дайын программалық өнімдерді (мысалы, электрондық кестелерді немесе арнайы математикалық пакеттерді) пайдаланып өткізу ыңғайлы. Программаны құрастырғаннан кейін оның көмегімен қателерді түзету мақсатында қарапайым тестілік есептерді (жауабы алдын ала белгілі болғаны жақсы) шешеміз. Егер нәтижелер эксперименттік деректерге немесе біздің интуициялық түсініктерімізге сай болса, программа бойынша есептеулер жүргіземіз. Сонан соң, нәтижелер жинақталып, өңделуі тиіс.

Егер ЭЕМ-де алынған кейбір үрдістің сипаттамалары эксперименттік нақтылықтың берілген дәрежесіне сәйкестенсе, модель нақты үрдіске тепе-тең келеді. Модель нақты үрдіске сәйкес келмеген жағдайда, алдыңғы кезеңдердің біріне қайтып ораламыз. Оның неғұрлым күрделі және нақтысын қолдану қажет. Өзгерістерді енгізгеннен кейін технологиялық тізбек бөлігінен тағы өтеміз де, қолайлы нәтижелер алғанша қайталай береміз. Бұл проблема модулдік принципті енгізу арқылы оңай шешіледі.

Модуль дегеніміз өз алдына компиляцияланатын, сипаттаудың әртүрлі компоненттерін (типтер, тұрақтылар, айнымалылар, процедуралар және функциялар) енгізу арқылы құрылатын жеке программалық бірлік. Модулдер қолданбалы программалар кітапханасын жасақтаудың және модулдік программалаудың қуатты тетігі болып табылады.

Біздің негізгі мақсатымыз - Turbo Pascal 7. 0 ортасының графикасын пайдаланып физикалық үрдістерді программалау арқылы есеп нәтижелерін компьютерде бақылау және зерттеу. Яғни, физикалық есептерді шығару үшін қажетті және жарамды моделдер құру.

1. 2 Компьютермен моделдеудің негізгі принциптері

Компьютермен моделдеу физикалық заңдылықтарды оқып-білудің тиімді әдістерінің бірі болып табылады. Компьютерлік моделдерді пайдаланып зерттеу көп жағдайда қарапайым және ыңғайлы болумен қатар, оның қойылуы мен нәтиже алуы қиындық келтірген жағдайлардың өзінде де жан-жақты сандық эксперименттер жүргізуге мүмкіндік береді. Компьютерлік моделдердің логикалық және формалдық сипаттары оның негізгі қасиеттерін анықтайтын негізгі факторларды табуға және физикалық жүйенің бастапқы шарттар мен параметрлердің өзгерістеріне әсерін зерттеуге жағдай жасайды.

Компьютерлік моделдеу, әуелі сапалық, содан соң сандық моделдерді құру арқылы құбылыстардың табиғатын абстракциялауды талап етеді. Оның соңында, компьютермен есептеу, эксперименттер сериясын жүргізу, нәтижелерді интерпретациялау, моделдеу нәтижелерін зерттеу объектісінің әртүрлі күйімен салыстыру, моделді дәлдеу мен жетілдіру және т. б. жұмыстар атқаруға тура келеді.

Компьютерлік моделдеудің кезеңдерін толығырақ келтірейік. Олар: есепті қою, моделденетін объектіні анықтау, концептуалдық моделді жасақтау, жүйенің өзара әсерлесетін, элементтері мен жай актларын анықтау, формалдау (математикалық моделге көшу), алгоритм құру, программа жазу, компьютерлік эксперименттерді жоспарлау және өткізу, нәтижелерді талдау және интерпретациялау.

Моделдеудің аналитикалық және имитациялық түрлері бар. Алгебралық, дифференциалдық және т. б. теңдеулерді пайдаланатын, немесе дәл шешулерін табуға әкелетін бірмәнді сандық процедураларды қолданатын реалды объектінің моделін аналитикалық деп атайды. Көп мөлшердегі элементар операцияларды тізбектеп орындау арқылы, зерттелетін жүйенің қызмет алгоритмін іске асыратын математикалық моделді имитациялық дейді.

Моделдеудің төмендегідей принциптері бар:

1. Ақпараттық жеткіліктілік принципі . Объект туралы қажетті ақпарат толық болмаған жағдайда оның моделін тұрғызудың мағынасы жоқ екендігі түсінікті. Жалпы, жүйе моделін тұрғызу ақпараттық жеткіліктіліктің белгілі бір деңгейіне жеткенде ғана мүмкін бола бастайды.

2. Орындалу принципі. Жасақталатын модель алға қойылған мақсатқа шекті уақыттың ішінде жетуді қамтамасыз етуі тиіс.

3. Моделдің көпшілдік принципі . Кезкелген модель реалды жүйенің кейбір қырларын ғана бейнелей алады. Зерттелетін үрдісті толық түсіну үшін оның бірнеше моделдерін жасақтау қажет болады. Әрбір жасақталған модель одан бұрынғы моделді анықтай түсуі керек.

4. Жүйелілік принципі. Зерттелетін жүйені стандартты математикалық әдістермен моделденетін, бір бірімен өзара қатынасы бар ішкі жүйелердің жиынтығы түрінде қарастыру мүмкіндігі болуы тиіс. Бұл жағдайда, жүйенің қасиеттері оның элементтерінің қасиеттерінің қосындысы болмауы тиіс.

5. Параметрлеу принципі. Моделдің ішкі жүйелері бір ғана параметрмен - вектормен, матрицамен, графикпен, формуламен сипатталуы мүмкін.

Жүйелерді компьютермен моделдеу дифференциалдық теңдеулерді шешуді жиі талап етеді. Мұндай теңдеулерді шешудің тиімді әдісі - торлау әдісі. Оған Эйлердің шекті айырмалар әдісі жатады. Бұл әдісте бір немесе бірнеше аргументтің үздіксіз өзгеру аймағы шекті түйін нүктелерімен (бір немесе көп өлшемді тормен) алмастырылып, арументі дискретті мәндерді қабылдайтын функциямен жұмыс жасалады. Олардың көмегімен туындылар мен интегралдарды жуықтап есептеуге мүмкін болады. Ол үшін 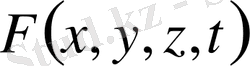функциясы мен оның аргументінің шексіз аз өсімшелері шекті, аз айырмалармен алмастырылады.

Физика есептерін шығару мен процестерді моделдеуде компьютер графикасы ерекше орын алады. Оның көмегімен әртүрлі сызбаларды дайындауға, денелер мен құрал-жабдықтарды кескіндеуге, тәуелділіктің графигін сызуға, денелердің қозғалыс траекторияларын бейнелеуге, берілгендер мен нәтижелерді түрлі түспен экранға шығаруға, жалпы айтқанда, процестерді имитациялық-графикалық моделдеуге болады. Ол үшін, Турбо Паскаль тілінің графикалық мүмкіндіктерін қарастырайық.

1. 3 Graph модулінің жалпы сипаттамасы

Турбо Паскаль тілінде графикалық жұмыстарды іске асыратын арнайы Graph модулі бар. Онда, IBM - типтес дербес компьютерлердің графикалық адаптерлерімен жұмыс істеуге есептелінген, графикалық процедуралар мен функциялар, тұрақтылар мен айнымалылар және типтер жинақталған. Турбо Паскалда графикалық драйверлер деп аталатын арнайы программалар ( BGI -файлдар) видеоадаптерлердің қалыпты жұмысын басқарады:

1 кесте. Драйверлер мен видеоадаптерлер

Көптеген видеоадаптерлер монитордың көрсету мүмкіндіктерін өзгерте алатын бірнеше графикалық режимде жұмыс жасай алады. Мәтіндік режимде экранда 40(80) × 25 символ бейнелеуге болатын болса, графикалық режимде онда бейнеленетін ең кіші объект - графикалық нүкте - пиксел деп аталынады. Мысалы: көп қолданылатын VGA адаптерінің қалыпты режимінде экранда 640 × 480 пиксел көрінеді және олардың 16 түсін айыруға болады.

• Uses Graphоператорын программа басына орналастырғанда ғана Graph модулінің қызметін толық пайдалануға мүмкіндік беріледі.
• InitGraph(Gd, Gm, Gol) процедурасы дербес компьютерге қойылған видеоадаптерді автоматты түрде тауып, сәйкес графикалық драйверді іске қосады және оны графикалық режимге көшіреді.

Мұнда Gol -драйвер файлына апаратын жол. Мысалы, Gol:=’’, Gol:=’c:\Tp7’ . Графикалық драйверлерді анықтау - Gd , ал олардың жұмыс режимдерін қою - Gm тұрақтылары арқылы жүзеге асырылады. Олардың мәндері мен қызметі төмендегі кестеде берілген:

2 кесте. Драйверлердің түрлері мен қызметі

• (қателік коды) нолден өзге мәні режимге көшу қателігін көрсетеді.
• CloseGraphпроцедурасы графикалық драйверді компьютер жадынан шығарып, видеоадаптерді мәтіндік режимге көшіреді.

1. 4 Компьютердің графикалық координаталар жүйесі

Графикалық режимде экранның ең кіші (бөлінбейтін) бөлшегі пиксель (нүкте) болады. Шындығында, олар, экранда тік төртбұрышты кесте түрінде реттеліп орналасқан, бір-біріне тәуелсіз, саны шекті, әртүрлі түспен жарықтана алатын, ара қашықтықтары өте аз және өлшемі кішкене шаршылар. Сондықтан да, графикалық экрандағы кескінді анықтап қарағанда оның өте кішкене шаршылардан (мозаика) құралатынын байқауға болады (1 сурет) .

1 сурет. Экрандағы кескінді үлкейтіп қарағандағы көрініс

Экрандағы нүктелердің (пикселдердің) орны олардың графикалық координаталары арқылы анықталады. Графикалық координаталар ретінде пикселдердің екі бағыттағы нолден басталатын реттік нөмірлері алынады. Мысалы, 640 × 480 режимінде экран әрқайсысында 640-тан 480 қатарға орналасқан нүктелерден құралатындықтан, x _гр , y _гр координаталары 0 ≥ x _гр ≥ 639, 0 ≥ y _гр ≥ 479 аралықтарында болады. x _гр координатасының мәні оңға, ал y _гр координатасының мәні төмен қарай өседі. x _гр , y _гр шектеулі бүтін оң мәндерді ғана қабылдайды (2-сурет) .

(0, 0) x _гр

2 сурет. Экрандағы координаталар жүйесі

y _гр (639, 479)

Нүктені экранда бейнелеу үшін оның декарттық ( x, y ) координаталарын графикалық ( x _гр , y _гр ) координаталарға

x _гр = x ₀ +x⋅m,

y _гр = y ₀ - y⋅n

формулаларын қолданып түрлендіруге болады. Мұндағы ( x ₀ , y ₀ ) графика-лық координаталар жүйесінің бас нүктесі, ал m, n - x және y остерінің бағытындағы масштабтар.

1. 5 Графикалық экран мен элементтердің параметрлерін қою

процедуралары мен функциялары

Турбо Паскалда экран мен оның графикалық элементтерінің әртүрлі параметрлерін қоятын, өзгертетін және сипаттайтын көптеген процедуралар мен функциялар бар. Олардың негізгілері төмендегі кестеде келтірілген:

3 кесте. Процедуралар мен функциялар

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс