Коши-Буняковский теңсіздігін қолдану арқылы республикалық математика олимпиадасының есептерін шешу

КОШИ-БУНЯКОВСКИЙ ТЕҢСІЗДІГІН ҚОЛДАНУ АРҚЫЛЫ РЕСПУБЛИКАЛЫҚ МАТЕМАТИКА ОЛИМПИАДА ЕСЕПТЕРІН ШЫҒАРУ

Батырбек Қайрат

Асатана қаласы, Сарыарқа ауданы

№61 орта мектебінің математика пәнінің мұғалімі

Теорема: Кез келген нақты 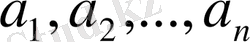және сандары үшін

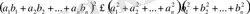
теңсіздігі орындалады. Бұл теңсіздікті Коши-Буняковский теңсіздігі деп атайды.

Дәлелдеуі: Берілген теңсіздіктен , 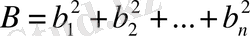деп белгілейік.

Кез келген нақты саны үшін

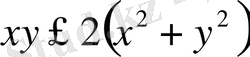
теңсіздігі орындалатыны белгілі. Ендеше, осы теңсіздікті қолданамыз:

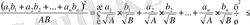
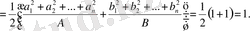
Осыдан,

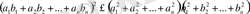
теңсіздігі алынады. Демек, теорема дәлелденді.

Мұнда, 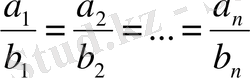болғанда теңсіздік теңдікке айналады.

Коши-Буняковский теңсіздігін көптеген есептерде мына теңсіздік

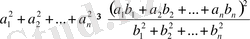
түрінде қолдануға тура келеді.

№1. Кез келген нақты 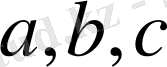сандары үшін

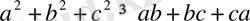
теңсіздігі орындалатынын дәлелдеңіз.

Шешуі: Коши-Буняковский теңсіздігін қолдану арқылы теңсіздікті дәлелдейміз:

Мұнда, 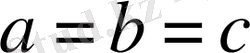болғанда теңсіздік теңдікке айналады.

№2. Кез келген нақты 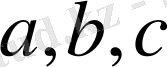сандары үшін

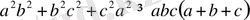
теңсіздігі орындалатынын дәлелдеңіз.

Шешуі: Берілген теңсіздіктің оң жаңын түрлендіріп, оған Коши-Буняковский теңсіздігін қолдану арқылы теңсіздікті дәлелдейміз:

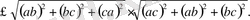
Бұдан,

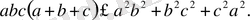
Мұнда, 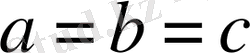болғанда теңсіздік теңдікке айналады.

№3. Кез келген оң 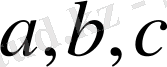сандары үшін

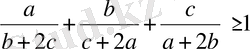
теңсіздігі орындалатынын дәлелдеңіз.

Шешуі: Коши-Буняковскийдің мына

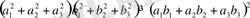
теңсіздігін қолданамыз.

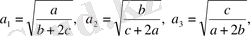
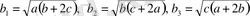болсын. Осы таңдап алған айнымалыларды Коши-Буняковский теңсіздігіне орналастырсақ, онда

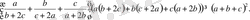
Бұдан,

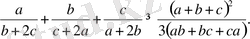
Енді, бұл теңсіздікті түрлендіріп, оған Коши теңсіздігін қолданамыз:

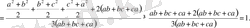
Демек, берілген теңсіздік дәлелденді.

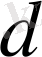№4. (Математика Республикалық Олимпиада-2009. ІІ-кезең, 10-сынып) Кез келген оң нақты және сандары үшін

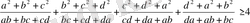
теңсіздігі орындалатынын дәлелдеңіз.

Шешуі: Коши-Буняковский теңсіздігін қолданамыз:

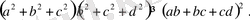
Бұдан,

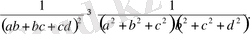
Соңғы теңсіздікті берілген теңсіздікке қолданамыз:

немесе

Осы теңсіздікке сәйкес қалған теңсіздіктерді жазамыз:

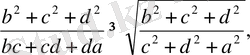
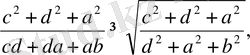
Бұл теңсіздіктерді берілген теңсіздікке орналастырып, оған Коши теңсіздігін пайдалансақ теңсіздік дәлелденеді.

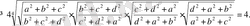
№5. (Математика Республикалық Олимпиада-2010. ІІ-кезең, 9-сынып) 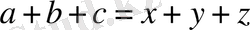теңдігі орындалатын теріс емес 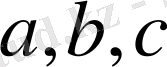және оң нақты 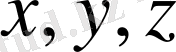сандары үшін

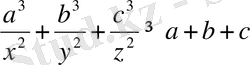
теңсіздігі орындалатынын дәлелдеңіз.

Шешуі: Алдымен берілген теңсіздіктің екі жағын 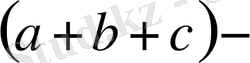ге көбейтіп, мына теңсіздік

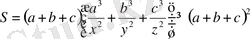
түрінде келтіреміз. Осы теңсіздіктің сол жағын түрлендіріп, оған Коши-Буняковский теңсіздігін қолданамыз:

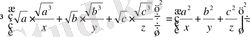
Енді, бұған Коши-Буняковскийдің теңсіздігін қолданамыз:

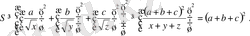
Бұдан,

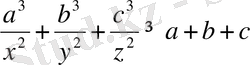
теңсіздігі алынады. Демек, теңсіздік дәлелденді.

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс