ДИНАМИКАЛЫҚ БЕЙБЕРЕКЕТТІК

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 52 бет
Таңдаулыға:

Бейсызықтық физика

КІРІСПЕ 3
1. ДИНАМИКАЛЫҚ БЕЙБЕРЕКЕТТІК 8
ЖАТТЫҒУЛАР 20
ӨЗІН-ӨЗІ БАҚЫЛАУҒА АРНАЛҒАН СҰРАҚТАР 23
ӘДЕБИЕТТЕР 25
2. ФРАКТАЛДАР 26
2.1. Фракталдық өлшемдiлiк 29
2.2. Моделдiк фракталдық объектiлер 36
ЖАТТЫҒУЛАР 47
ӨЗIН-ӨЗI БАҚЫЛАУҒА АРНАЛҒАН СҰРАҚТАР 48
ӘДЕБИЕТТЕР 50
3. ИНФОРМАЦИЯ МЕН ЭНТРОПИЯ КҮРДЕЛI ЖҮЙЕЛЕР ФИЗИКАСЫНДА 51
3.1. Информация ұғымы физикада 51
3.2. Информациялық энтропия 57
3.3. Ашық жүйелердегi өзқауым дәрежесiнiң белгi-шарты 60
3.4. Реттiлiк пен бейберекеттiк үйлесiмдiлiгiнiң әмбебап мөлшерлiк
белгi—шарттары 62
ЖАТТЫҒУЛАР 66
ӨЗІН-ӨЗІ БАҚЫЛАУҒА АРНАЛҒАН СҰРАҚТАР 68
ӘДЕБИЕТТЕР 70

КІРІСПЕ

Қазіргі кезде “бейсызық физика” ғылыми жұртшылық түгелдей қабылдаған
термин. Дүние жүзіндегі жетекші ғылыми басылымдардың бәрінде осылай аталған
арнайы тараулар бар. Бейсызық физика пәнінің мазмұнын, сыртқы ортамен
энергиямен және информациямен үнемі алмасып отратын, ташық, сызықты емес
жүйелердің статистикалық физикасы анықтайды.
Физикалық тұйық жүйелерде, эволюция –табиғат пен қоғамда жүретін
өзгерістер мен даму процестері, біршама уақыттан соң тепе-тең күй орнайды.
Тепе-тең күйлерде жүйенің макроскопиялық параметрлері (көлем, қысым,
температура және т.б.) уақыт бойынша және кеңістікте өзгермейді.
Молекулалық деңгейде бұл күйге, Больцманның пайымдауынша, бей-берекеттіктің
ең жоғарғы мәні сәйкес. Себебі, тепе-тең күйлерді бірінен-бірін бірмәнді
ажырату мүмкін емес. Зерттеулер, табиғатта қоршаған ортамен энергия мен
информация (информация жөнінде мағұлымат 3-ші тарауда келтірілген) алмаса
алатын органикалық және органикалық емес күрделі ашық жүйелердің көп
болатынын көрсетіп отыр. Олардың кейбірі құрылымы жағынан күрделі болса,
екіншілері атқаратын функциялары байланысты күрделі.
Ғылымның әртүрілі саласынан күрделі жүйелердің мысалын көптеп
келтіруге болады. Мысалы, физикада затттың газ күйі, құрылымы жағынан өте
күрделі, себебі, көп молекулалардан құралады және олар, бірімен-бірі өзара
соқтығысулар нәтижесінде, ретсіз, хаосты қозғалады. Химиялық реакцияларға
да өте көп молекулалар қатысады және рекомбинация нәтижесінде жаңа
молекулалар түзіледі. Биологияда клеткалар, құрылымы жағынан күрделі
мембраналардан, ядролар мен цитоплазмалардан құралады. Техникада әртүрілі
қозғалтқыштар, машиналар мен зауыттар және т.б. жасанды күрделі жүйелер
болса, экономика өзінің ақша айналысымен, өндірістерімен, заттарды тасуы,
тұтынуы және сақтауымен күрделі. Психология айналысатын адамның мінез-құлқы
мен білімнің әртүрілі саласын қамтитын ғылым да күрделі жүйелер. Аталған
ғылым салаларын құрайтын бөліктер өзара үйлесе қызымет атқарады.
Барлық күрделі жүйелерге тән, оларды біріктіретін жалпы принципті
айқындауды, ғылымның әр саласында орын алған, күрделі объектілерді зерттеу
арқылы жүзеге асыруға болады. Бірақ осы әмбебап заңды қай деңгейде
тұжырымдаған жөн –микроскопиялық түрде ме, әлде макроскопиялық тұрғыда ма?
Мұны білу өте маңызды, себебі, бір жүйені сипаттау барысында әртүрілі
жауаптар алынады. Мысалы, микроскопиялық көзқарас бойынша, газ ретсіз
қозғалатын молекулалардың жиыны, ал макроскопиялық тұрғыда ол біртекті.
Ғылымның соңғы жетістіктері, күрделі ашық жүйелерде, әртүрілі
өздігінен реттелген құрылымдар пайда болатынын дәлелдеді. Мұнда негізгі
рөлді, жүйе энергиясының шашрауы мен информацияның жоғалуына әкелетін,
диссипация атқарады. Осының аса маңыздылығын нақтылау үшін физик-теоретик
И. Пригожин “диссипативтік құрылым” ұғымын енгізді. Қоршаған ортадан,
бейберекеттіктен энергия алатын және алдыңғы бұзылған объектіден де
күрделі, жаңадан пайда болған құрылымдар–диссипативтік деп аталады. Ашық
жүйелердің күрделілігі оларда ұжымдық құбылыстардың жүруіне, оларды
құрайтын бөліктердің үйлесе қимыл жасауына кең жол ашады. Жүйені құрайтын
элементтердің үйлескен қаракетінің арқасында диссипативтік құрылымдар
түзілуін ескерген физик Г. Хакен, өзқауым процестерін, жалпы түрде
синергетика (грекше sinergetike–үйлесе қимылдау, бірігіп қаракеттену) деп
аталады. Ол “өзқауым–бейберекеттіктен пайда болатын реттелген
жоғарықұрылымдардың түзілуі” – деп түсіндірді. Яғни, өзқауым, жүйенің өзара
үйлескен қаракетінің нәтижесінде, ретсіз күден өздігінен реттелген күйге
өту процесі. Ашық күрделі жүйелерде өзқауым процесінің жүруіне негізгі
себепшілер ықтималдық пен кездейсоқтық. Реттелу ауытқулардың нәтижесінде,
ал орнықтылық орнықсыздықтан пайда болады. Бейберекет күй энтропия мен
информация арқылы сипатталатын анықталмағандықтан–ықтималдық пен
кездейсоқтықтан тұрады.
Ашық жүйелерде энергия (зат пен өріс) ағынын өзгертіп отыру арқылы
өзқауым процесін, яғни, диссипативтік құрылымдардың пайда болуын реттеп
отыруға болады. Құрылым түзілуінің негізінде екі қарама-қарсы процестің
қатар жүруі: біріншіден, үздіксіз ортада кездейсоқ сыртқы әсерді (энергия
мен информация көздері) қостайтын біртексіздіктің артуы, ал екіншіден, осы
біртексіздікті жоюға тырысатын диссипативтік бастаманың пайда болуы. Даму
орнықсыздық, бифукация (жүйенің басқа сапалық деңгейге ауысуының көп
вариантты мүмкіндігін тудыратын критикалық нүктелердің пайда болуы) және
кездейсоқтық күшті тепе-теңсіз жүйелердің дамуымен сипатталуына ерекше рөль
атқарады. И. Пригожин “бейберекеттіктен реттілік тудыратын–тепе-теңсіздік”,
– деп санайды.
Ашық жүйелердің ең қарапайым және маңызды мысалы ретінде тірі
организмдер саналады. Биологиялық жүйелердің негізгі ерекшелігінің өзі,
оған сыртқы ортадан келетін және ол шашырататын энергия ағынының арқасында
өзқауым процесінің жүруі. Осының нәтижесінде, биологиялық жүйелер өздігінен
жаңа күрделі құрылымдар түзуге мүмкіндік алады. Бұл термодинамика заңдарына
қайшы келмейді, себебі, биологиялық жүйелер, сыртқы ортамен энергия, зат
және информация алмаса алатын, ашық жүйелер. Ал ашық жүйелерде, энтропияның
өсу заңы деп аталған, термодинамиканың екінші заңына қарсы процестер жүреді
және соның нәтижесінде, бейберекеттік өлшемі–энтропия уақытқа байланысты
кемиді.
Өзқауым эффектілері, тек биологиялық объектілерде ғана емес, әртүрілі
формаларда органикалық емес жүйелерде де жүреді, деп болжам жасауға толық
мүмкіндік бар. Бейсызық физика мен синергетика, жүйені құрайтын жеке
бөліктердің ортақ қасиеттерін анықтайтын және олардың өзара әсерлесу
заңдылықтарын тағайындайтын математикалық нобайларды (моделдерді)
зерттейді. Зерттелетін орталардың қасиеттеріндегі негізгі айырмашылық
оларда жүретін өзқауым процестері. Сондықтан синергетиканы–табиғаттағы және
өзқауым теориясы ретінде қарастырады.
Синергетика, объектілердегі қарқынды өзара әсерлер мен құрылымдардың
түзілу процесін зерттейтін ғылыми бағыт. Бұл құбылыс, сыртқы ортамен
қарқынды түрде энергия мен информация алмасатын, нәтижесі өзқауым,
реттілік, энтропияның кемуі арқылы жүйенің эволюциясына әкелетін, тепе-
теңсіз ашық жүйелерде жүзеге асады. Жаңадан пайда болған құрылымдардың,
кіші қозуларға байланысты орнықтылығын, оның бейберекеттіктен өзгешелігінің
белгі-шарты болып табылады. Егер бұндай орнықтылық жоқ болса, жүйені
зерттеудің статистикалық әдісі қолданылады.

1. ДИНАМИКАЛЫҚ БЕЙБЕРЕКЕТТІК

Молекулалық деңгейде, бейберекеттіктің ең жоғарғы мәні, жүйенің тепе-
тең күйіне сәйкес келетіні жоғарыда айтылғанды. Физикада, биологияда,
экономикада және т.б. "бейберекеттік" теріс мағынаға ие. Бірақ, кейде тепе-
тендіктен алыс күйлердегі қозғалыстар да бейберекет қозғалыстар деп
аталады. Оған сұйықтар мен газдардың құбырдағы қозғалысы жатады.
Ю.Климонтович "динамикалық бейберекеттікті" салыстырмалы қарапайым
динамикалық жүйелердегі күрделі қозғалыстарды сипаттауға қолдануға
болатынын дәлелдеді. "Динамикалық" деген сөз, бастапқы ауытқулардың, яғни,
ретсіздік көздерінің жоқтығын білдіреді. Осы себепті, "динамикалық жүйе"
белгілі қездейсоқтық орын алатын, реал ретсіз қозғалыс "физикалық
бейберекеттік" деп аталады. Бұның айқын мысалы, тепе-тең күйдегі атомдар
мен молекулалардың қозғалысы.
Динамикалық бейберекеттікті, конвекциялық жылу алмасудың математикалық
нобайы ретінде, алынған теңдеулерді зерттеу барысында, бірінші байқаған
Э. Лоренц. Егер сұйық қабатын төменгі жағынан қыздыратын болса, ауырлық
күші мен температүра градиентінің үйлесімді қаракетінің нәтижесінде, онда
конвекциядық, ағын пайда болады. Бастапқыда, ыдыс түбі мен сұйық бетінің
арасындағы температүра айырымы аз кезде, сұйық қабатындағы жылу берілу жылу
өткізгіштік әсерінен жүзеге асады. Ал, температүраның қайсыбір кризистік
мәнінде, сұйықта реттелген құрылымдар (Бенар ұяшықтары) түзіледі және
макроскопиядық қозғалыс орын алады. Осының нәтижесінде, ұяшық ішіндеп
сұйықтын, қызған бөліп жоғары, ал оның шеттеріндегі суықтау бөліп төмен
қозғалады. Біршама уақыттан соң, осы екі қарама - қарсы ағынның кеңістік
таралуы өздігінен реттеліп, сұйықта қайсыбір квазистационар күйдегі жылулық
ағын орын алады.
Кейінгі зерттеулер, бастапқы шарттардың өте аз өзгерісі, жүйенің
қозғалыс сипатын елеулі өзгерістерге ұшырататынын, ал олардың шекті
дәлдікпен берілуі қозғалыс сипатының даму жолын болжаудың мүмкін еместігін
көрсетті. Олай болса, бастапқыдағы кіші қозулар, уақытқа сәйкес өсіп
отыратын болса, жүйенің күйі тек ықтималдық, тұрғыда сипатталады. Ашық
жүйелерді зерттеудің бұл жолы, динамикалық бейберекеттіктің қазіргі
көрінісінің негізін қалайды.
Сыртқы айнымалы күштердің әсерінен (мысалы, үйкеліс күшінің) дененің
қозғалысы, жылдамдық бірмәнді болмайтын, күрделі сипатқа ие болады. Бұл
кезде жүйснің қозғалысы, ие сипаттайтын теңдеудің бірнеше шешімі болуы
мүмкін. Онда реттелген күй — динамикалық, бейберекеттік орнайды. Соңғы
кездері физикалық, химиядық, биологиялық, педагогикалық, әлеуметтік және
т.б. жүйелерде бейберекеттік күйлер басым болатындығы анықталды. Осы
айтылғандардан, күрделі жүйелердегі іргелі заңдылықтарды түсіндіру мен
баяндаудың арнайы әдістемесі қалыптасуы тиіс..
1.1. Бейсызық маятник. Динамикалық жүйелердің стохасталынуы
Механикалық, жүйелердегі периодты тербелмелі қозғалыс заңдары, осы
жүйенің қасиеттерімен және оған ықпал ететін сыртқы күштердің сипатымен
анықталады. Егер тербелмелі процесте жүйенің күйін сипаттайтын параметрлер
тұрақты қалып, оған әсер етуші күштер, осы параметрлерге байланысты сызықты
функциялармен өрнектелсе, тербелмелі жүйелерде және тербелістерде сызықты
болып саналады. Тербелістегі денені тепе-тең күйге қайтарушы күш ығысуға
байланысты сызықты функциямен өрнектелсе, оның тербелісі гармониялық деп
аталады. Мұндай периодты күштердің қатарына, жылдамдықтың, бірінші
дәрежесіне тәуелді үйкеліс күштері (F = -((), серпімдік күштері (F -
kx) және т.б. жатады.

1-сурет.
Математикалық
маятник.
Сызықты маятниктің ең қарапайым түрі математикалық маятник. Ол
созылмайтын жеңіл ұзын жіпке ілінген, массасы m, өзі ілінген жіптің
массасымен салыстырғанда әлдеқайда үлкен, ал өлшемдері, математикалық
маятниктің ұзындығынан l әлдеқайда кіші, жүктен тұрады (1-сурет). Тепе-тең
күйден φ бұрышқа ауытқыған математикалық маятниктің өз еркіне жіберілген
кездегі қозғалыс теңдеуі былай жазылады:
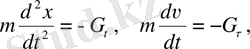(1)
мұнда G(= mg sin φ - маятникті тепе-тең, күйге қайтарушы
күш. Суреттен, тербелістегі нүкте қозғалысы мына формуламен анықталатыны
көрінеді:

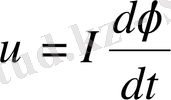
Осыны (1) теңдеуге кою арқылы оны мына түрге
келтіруге болады: :
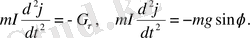(2)
Бұл теңдеудің оң жағында дененің массасы мен маятниктің ұзындығына бөлу
арқылы оны мына түрде жазуға болады:
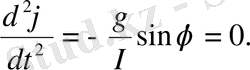(3)
Жалпы түрде (2) теңдеудің шешімін табу күрделі болғандықтаң оның жеке
жағдайлары қарастырылады. Мысалы, маятниктің тепе-тең күйден ауытку бұрышы,
онын синусына пропорционал болатындай, кіші деп саналады. Бұл кезде, 1-ші
суреттен көрінгендей, 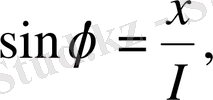яғни, нүктенің доға бойымен ығысуы, жуық
шамамен, горизонталь хорданын, ұзындығына х тең. Осыны кою арқылы (2)
теңдеудің соңғысын мына түрге келтіреді:
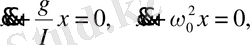(4)
бұл жерде 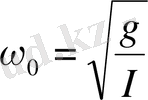- дөңгелек немесе циклдік жиілік, ал (4)
теңдеу сызықты математикалық маятниктің қозғалыс теңдеуі деп аталады.
Серпімді серіппеге бекітілген жүктің тербелісін, заңдылығы да (4) теңдеумен
сипатталады және осы жүйе сызықты осциллятордың моделі болып саналады.
Тригонометриялық, функциялар sin (t мен соs (t (4) теңдеудің дара
шешімдері екендігі белгілі. Сызықты теңдеулердің шешімдерінің қосындысы мен
қайсыбір шешімінің тұрақты шамаға көбейіндісі, олардың шешімін береді.
Сондықтан, (4) теңдеудің жалпы шешімі мына түрде жазылады:

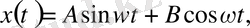
Мұндағы А және В - тұрақты шамалар. Бұлар гармониялық функциялар деп
аталады. Түрледірулер арқылы, гармониялық тербелістің жалпы теңдеуі (4)
мына түрге келтіріледі:
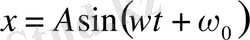немесе
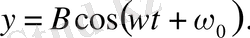
Мұндағы А, В - тербеліс амплитудалары, 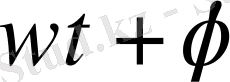- оның фазасы, ал -
тербелістің бастапқы фазасы.
Егер қозғалыстағы денеге үйкеліc күші немесе сыртқы айнымалы күштер
әсер етсе, оның жылдамдығы ылғи да бірмәнді болмайды. Бұл кезде дене
қозғалысын сипаттайтын динамикалық теңдеудің әртүрлі шешімдері болуы
мүмкін. Мұндай физикалық жүйелерде бейберекет күй — динамикалық хаос
орнайды. Соңғы жылдары мұндай заңдылықтар тек физикалық жүйелерде ғана
емес; химиялық, биологиялық, тіптен әлеуметтік жүйелерде де орын алатындығы
белгілі болды. Осы іргелі заңдылықты түсіну мен түсіндірудің ең тіке және
қарапайым жолы бейсызық, маятниктің қоғалысын қарастыру.
Сонымен, егер маятниктің тербеліс амплитудасы ілеулі мәндерге жетсе,
яғни, тербелістен денеге әсер етуші үйкеліс күші, жылдамдықтың бірінші
дәрежесіне емес, үлкен жылдамдықтарда жүзеге асатын, екінші дәрежесіне
тәуелді болса, жағдай күрт өзгереді. Үлкен ауытқуларда маятниктің тербелісі
сызықты болмайды. Яғни, бейсызық, тербелмелі жүйенің қозғалысы гармониялық,
тербелмелі қозғалыстан өзгеше және маятниктің, тербеліс амплитьудасы өскен
сайын бұл өзгешелік ұлғая береді. Сондықтан, тепе—тең күйден үлкен бұрышқа
ауытқыған денелер, нүктелер үшін, жуықталған (4) теңдеуді пайдалануға
болмайды. Бұл жағдайда нүктенің тербелісі периодты болғанымен гармониялық
емес. Демек, маятнитің тербеліс периоды, оның ауытқуына тікелей тәуелді.
(3) теңдеудің эмбебап мағынасын ескере отырып, айнымалы х арқьлы
белгіленеді, яғни ( = х деп алынады. Мұнда мына интервалда өзгереді.
Олай болса, математикалық, маятниктің қозғалысы бейсызық, теңдеумен (3)
сипатталады:
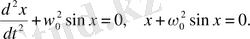(6)
Осыдан, тербелістегі дененің тепе—тең қалыптан елеулі ауытқу
бұрыштарында, жалпы түрдегі шешімі бірмәнді емес, (6) теңдеу пайдаланылады.
Бұл теңдеуді кезеңдік (фазалық) кеңістікте (жылдамдық-коортдината
айнымалылар кеңістігінде) қарапайым талдау, сапалық тұрғыда, жаңа нәтижелер
тағайындауға мүмкіндік береді. Бұл уппн (6) теңдеу, әрқайсысы бірінші
реттік екі дифференциалдық теңдеулер арқылы жазылады:
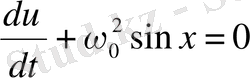және
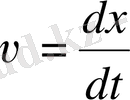
(6) теңдеудегі уақыт дифференциалын 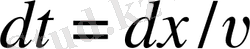алмастыру арқылы мынадай
өрнек алынады:
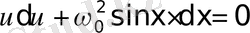(7)
Алынған теңдеуді 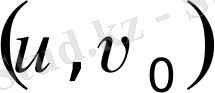және 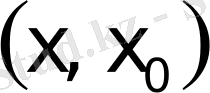шектерінде интегралдау, тербелістегі
дененің. бірлік массасына сәйкес толық энергияны береді:
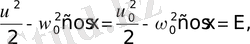(8)
мұндағы 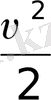- тербелістегі бірлік массалы дененің, кинетикалық
энергиясы, 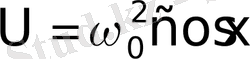– оның потенциалдық энергиясы. Тербелмелі жүйенің Тепе-тең
күйі мына шарттан анықталады:
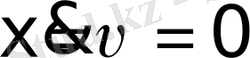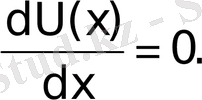яғни (9)
Бұл, тепе—тең күйде тербелістегі дененің жылдамдығы нөлге тең
болатынын, ал оның потенциалы 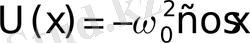экстремумға ие екендігін білдіреді (2а
- сурет). Сондықтан маятниктің тепе-тең күйі мынадай теңдеулермен
сипатталады: , 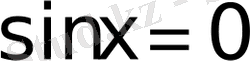Демек, , , ал 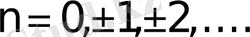Тепе-тең күйде х
нүктесінің жылдамдығы нөлге тең, ал оның потенциалы , n-нің жұп
мәндерінде минимумға, ал тақ мәндерінде максимумға ие. Олай болса, n - нің
жұп мәндерінде тербелістегі нүктенін, траекториясы эллипс тәріздес, ал тақ
мәндерінде гиперболалық болады (2-сурет).

2 - сурет. Нүктенің периодты потенциалы (а) және соған сәйкес фазалық
суреті (б).

(8) теңдеуді түрлендіру арқылы оны мына түрде өрнектеп жазуға болады:
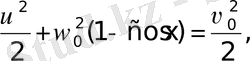10
бұл кезде нүкте жылдамдығының ( ығысуға х күрделі тәуелділігін
анықтайтын теңдеу алынады. (10) теңдеуден нүкте тербелісінің траекториясы
2а суретте кескінделген графикпен сипатталатыны байқалады. Мұнда нүктенің
жылдамдығы бірмәнді емес, және нүктелерінде график тарамдалып
кетеді.
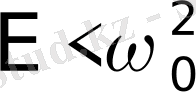мәндерінде кезеңдік жазықтықтағы траекториялар ((=((х)
тәуелдігі), маятниктің тербелісін сипаттайтын тұйық сызықтарды береді
(финиттік қозғалыс). Бұл кезеңдік траекториялар, потенциалдық шұңқырда
финиттік (периодты) тербеліс жасайтын "арқандалған" бөлшектерге сәйкес
келеді (2б-сурет). Кезеңдік траекторияларда ерекше нүктелер пайда болады:
центр типті (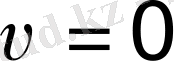, ); және ер, тұғыр типті (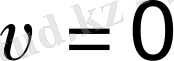, 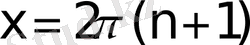), мұнда

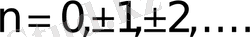
Нүктені қоршайтын қандай да бір аумақ, бірімен-бірі қиылыспайтын тұйық
кезеңдік траекториялармен тегістей толтырылса, ондай ерекше нүкте центр деп
аталады. Қарастырылатын нүктенің қандайда бір аумағын жеке облыстарға
бөлетін, өздерін берілген теңдеуімен сипатталатын гиперболалар
жиынына сәйкес ұстайтын, осы кезеңдік траекториялардың шекті саны түйісетін
ерекше нүкте тұғыр деп аталады.
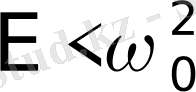мәндерінде кезеңдік траекториялар, қозғалыстары шектелген
(инфинитті) "өткінші" бөлшектерге жатады. Бұларда, кезеңдік траекториялар,
толқындық, сызықтарға айналады және математикалық маятниктің айналмалы
(инфинитті) қозғалысына ұқсас келеді. 2б- суреттен, оның, жылдамдықтың
қайсыбір мәнінің маңында жүретін, периодты тербеліс екендігі және кезеңдік
қисықтардың жоғарғы және теменгі бұтақтарына жылдамдықтың әртүрілі
бағыттары сәйкес келетіндігі байқалады.
Фазалық жазықтықта траекториялардың әртүрілі типтері, сепаратриса
(сарапшы) деп аталған, ерекше қисықтарға бөлінді. Біздің жағдайда
сепаратрисаға, 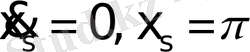нүктелері арқылы өтетін, кезеңдік траекториялар
жатады. Сондықтан, оған энергиясы 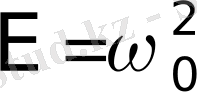және қозғалысты екі әртүрілі типке
бөлетін нүкте сәйкес келеді.
Сепаратрисадағы қозғалыс теңдеуінің шешімін табу қиын емес. Ол үшін
(8) теңдеудегі 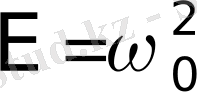деп саналады және одан 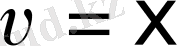мәні анықталады. Олай
болса, тербелістегі бөлшектің жылдамдығы былай анықталады:.
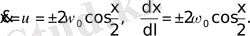(11)
(13) теңдеу, мынадай бастапқы шарттарда айнымалыларға бөлу
әдісі арқылы, интегралдаудан соң, мына түрге келеді:
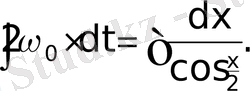(12)
Онша күрделі емес түрлендірулерден соң (12) теңдеуден тербелістегі
бөлшектің ығысуын анықтауға мүмкіндік беретін өрнек алынады:
(13)
(13) өрнек сепаратрисаның теңдеуі (екінші біріншідегі уақытты
–ға алмастыру арқылы табылды).
Сепаратрисадағы бөлшек қозғалысының динамикасы туралы толықырақ
мағұлымат, оның жылдамдығын 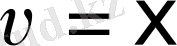анықтайтын өрнекті талдау барысында,
алынады. Осыдан, (11) теңдеуді қолдану арқылы, (13) теңдеуден
сепаратирисадағы нүктенің жылдамдығын анықтайтын өрнек алынады:

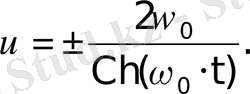
Гиперболалық косинус арқылы өрнектелген (14) теңдеу, бейсызық ортада
пайда болатын, оқшауланған толқынды – солитонды сипаттайды (3-сурет)
Жылдамдық пішінінің сипатты ені ( Оның шеттері -те
экспоненциалды төмендейді Плюс таңба оңға қозғалатын слитонға сәйкес
(фазалық жазықтықтағы сепаратрисаның жоғарғы бұтағы (2б-сурет) ал минус
таңба солға қарай қозғалатын солитонды береді.

3-сурет. Сепаратрисадағы
жылдамдықтың солитон тәріздес
шешімі
Солитон-бейсызық ортада таралатын оқшау орнықты құрылымды толқын
Салитондар өздерін бөлшек сияқты ұстайды (бөлшек тәріздес толқын) Олар
бірімен-бірі немесе басқа қайсыбір қозулармен әсерлесу барысында бұзылмайды
құрылымын бұрынғы қалпында сақтай отырып жайылады.Теориялық және
тәжірбиелік түрде көптеген бейсызық орталарда (сұйық,плазма, қатты дене
және т.б. ) түзілетін салитлондар табылған. Салитонның мысалдары ретінде
алып құйындарды (циклондар мен анти циклондар ), нерв талшықтарында
түзілетін импульстер – аксондар, өте аз уақыт өмір сүретін ядролық
резонанстық бөлшектерді алуға болады.

Солитон түсінігі қазіргі физикада кеңінен қолданылатын квазибөлшек
түсінігімен тығыз байланысты және оның бейсызық ортадағы арнаулы түрі болып
табылады. Квазибөлшектер бейсызық ортадағы элементар қозулар, ұйтқулар,
бөлшек тәріздес шоғырланған толқындар. Олай болса, квазибөлшектің пайда
болуы, табиғаты әртүрлі (механикалық, электромагниттік және т.с.с.)
әсердің, импульстің ортада жоғалмай таралуы. Квазибөлшектер ылғида
қозғалыста болады. Сұйықтарда турбон, қатты денеде фонон, плазмада плазмон,
магнитик ортада магнон, шала өтгізгіштерде экситон, асқын аққыш орталарда
ротон және т.с.с. квазибөлшекпн, мысалдары болып табылады. Тұрақталған
периодты тербелістердің математикалық бейнесі шектік цикл, ал квазипериодты
тербелістердікі инвариантты тор. Тор деп дөңгелек тесік фигура айтылады, ал
инвариаиттық деген сөз, оның динамикалық жүйенің сақталу заңына
сәйкестігін білдіреді. Орнықты циклде, инвариантты торда, барлық жақын
траекторияларды өзіне тартатын объектілер - аттракторлар. Орнықты
қозғылысты сипаттайтын, тұйық фазалық, траекториялар аттракторлар (ағылшын
тілінен қазақшаға аудармасы "тартушы объектілер") деп аталады. Яғни,
аттракторлар жүйе өздігінен ұмтылатын жинақтаушы қасиеті бар объектілер.
Оған кезеңдік кеңістіктегі шектік циклдер мен қозғалмайтын нүктелер жатады
(2-сурет). Сонда, периодты қозғалыстан ауытқыған жүйелер; біршама уақыттан
соң, сол қозғалысқа қайта түседі, (мысалы, сағат маятнигі).
Бейсызық консервативті (диссипация орын алмайтын) жүйенің жоғарыда
қарастырылған мысалында қозғалыс сипаты бірмәнді болмағанымен қандай да бір
орнықтылық, пайда болады. Бұның себебі, бастапқы мәндердің аз
өзгерістерінде, кезеңдік нүктенің ауысатын траекториясының, оның
алғашқыда қозғалған траекториясына өте жақын орналасуында.
Диссипацияның болуы қозғалыстың кезеңдік сипатын сапалық тұрғыла
өзгертеді. Кәдімгі аттрактор, өте күрделі құрылымы бар әуейі (странный)
аттракторға айналады. Бұл кезде барлық траекториялар уақыт бойынша оның
әрбір нүктесі арқылы өтетін, бастапқыда біріне-бірі барынша жақын
нүктелердің арасы жеткілікті уақыттан соң елеулі қашықтыққа айналады. Әуейі
атгракторларды алғаш рет, сұйықтардың жылулық-конвекциясының
қарапайымдалған үш өлшемді теңдеулерінің негізінде, Е.Лоренц байқаған.

ЖАТТЫҒУЛАР

1. Сепаратрисадағы бөлшектің жылдамдығын (11) анықтандар.
Нұсқау. Сепаратрисадағы қозғалыс теңдеуінің шешімін табу қиын емес. Ол
үшін (8) теңдеудегі деп саналады және одан 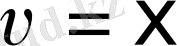мәні анықталады. Бұл
мына жолмен жүзеге асырылады.

себебі, 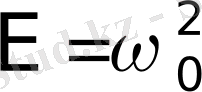. Бірақ,

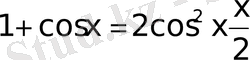
екендігін ескеріп және оны (10) теңдеуге қою арқылы мынадай өрнек алынады:

бұл теңдеуден нүктенің жылдамдығын анықтауға мүмкіндік беретін формула
табылады:
(11)
2. Сепаратриса теңдеуі деп аталатын тербелген нүктенің ығысуын (13)
табындар.
Нұсқау. (11) өрнек, мынадай бастапқы шарттарда t=0, х=0, айнымалыларға
бөлу әдісі арқылы интегралдаудан соң былай жазылады:
(12)
Бұл теңдеудің оң жағындағы интегралдың бөліміндегі шама мынаған тең:

Жоғарғы теңдеудегі деп белгілеу арқылы, оны мына түрге келтіруге
болады:

aл

Мұнан

Осыларды (12) теңдеу оң жағына қойып және сәйкес түрлендірулер жүргізу
арқылы, оң жағы анықталады, яғни:

Бұл алынған мәндерді (12) теңдеуге қойып және интегралдаудан соң
мынадай өрнек алынады:

Осыдан

aл
(13)
Соңғы теңдеу нүктенің ығысуын анықтауға мүмкіндік береді:
(13) өрнек сепаратрисаның теңдеуі (екіншісі біріншідегі уақытты t( - t-
ға алмастыру арқылы табылады.
3. Сепаратрисадағы бөлшектің қозғалысының динамикасы туралы толығырақ
мағлұматты, оның жылдамдығын анықтайтын өрнекті талдау барысында
алуға болады. Бұл үшін мәнін анықтауға мүмкіндік беретін, (13)
теңдеуден анықталатын ығысудың х мәні пайдаланылады:

Бұл жерде

олай болса

Бұл теңдеуді пайдалану арқылы, сепаратрисадағы бөлшектің жылдамдығы
анықталатын (13) формула мына түрде жазылады:
(14)

ӨЗІН-ӨЗІ БАҚЫЛАУҒА АРНАЛҒАН СҰРАҚТАР

1. Бейсызық деп қандай маятник айтылады және оның қозғалыс теңдеуі
қалай өрнектеледі?
2. Жиын элементтерінің арасындағы сәйкестікті табыңдар:

Терминдер Қысқаша мағынасы
1) Динамикалық бейберекеттік А. Тепе-тең күй
2) Физикалық бейберекеттік В. Бейсызық динамикалық жүйе
3) Реттілік С. Сыртқы ауытқулардың болуы
4) Ретсіздік D. Тепе-теңсіз күй
Е. Реттелген бейберекеттік

3. Жиының қандай элементтері диссипативті жүйенің қасиетін анықтайды?
А. Ашық (тұйықталмаған).
В. Оқшау (тұйықталған).
С. бейсызықтық.
D. Тепе-теңдік.
Е. Тепе-теңсіздік.
4. Жиын элементтерінің сәйкестігін анықтандар:
Энергия үшін қойылатын шарттар Қозғалыс түрлері
1) А. Маятниктің тербелісін сипаттайтын
финиттік қозғалыс
2) В. Оқшау толқын – солитон
3) С. Винт тәріздес қозғалыс
D. Маятниктің айналмалы қозғалысы,
инфинитті қозғалыс

5. Аттрактор, әуейі аттрактор деген не?
6. Қандай нүктелер бифуркациялық деп аталады?
7. Тұйық жүйе мен ашық жүйенің айырмашылығы неде?
8. Стохастылық деген не?
9. Қандай құбылыстар бейсызық деп аталады?
10. Қандай құрылымдар диссипативтік деп аталады және олар қалай пайда
болады?

ӘДЕБИЕТТЕР

1. Пригожин И.,Cтенгерс И.Порядок из хаоса.-М.:Прогресс.-1986.-256 с.
2. Хакен Г.Информация и самоорганизация.-М.: Мир.-1991.-240 с.
3. Климонтович Ю.К.Статистическая теория открытых систем.-М.:Янус.-1995.-
624 с.
4. Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику.-М.:Накуа.-
1988.-368 с.
5. Николис Дж. Динамика иерархических систем. Эволюционное представление.-
М.:Мир.- 1989.-486с.
6. Жанабаева З.Ж. Лекции по нелинейной физике.-Алматы:Қазақ университеті.-
1997.-72с.

2. ФРАКТАЛДАР

Көп жағдайда, физика ғылымының дамуы күрделі жүйелердiң макроскопиялық
құрылымы мен ондағы микроскопиялық процестер арасындағы байланысты ашудың
дәлдiгiнде. Салыстырмалы түрде бұндай байланысты тағайындаудьң екi, толық,
жетiстiкке жеткiзетiн мүмкiндiгi бар. Ол жүйе толық, реттелген күйде немесе
абсолют бейберекеттiкте. Ретсiз орталар мен кеңiстiк—уақыт өлшемнiң
корреляцияланбаған кең диапазондарында бұндай мүмкiндiк жоқ, немесе бұл
шарт орындалмайды.
Табиға кездесетiн, өлшемдерi атомдық масштабтан әлемдiк кеңiстiкке
дейiн созылып жатқан, сан қилы объектiлердің (нысандардың) геометрия бiздің
оны зерттеп түсіну үшін құратын, идеалдандырылған моделдерiмiзде басты орын
алады. Бірақ, дәстүр бойынша табиғат геометриясын инидуктивті түсiнудің
негiзi ретiнде, осы уақытқа дейiн, евклидтiк геометрияның түсiнiктерi,
сызық шеңберлер сфералар мен тетраэдрлар қолданылады.
Осындай күрделi жүйелерде болатын процестердi құрылымды—стохастикалық
құбылыстарды барынша қарапайым түрде сипаттауға, түсiну мен түсiндiруге
мүмкiндiк беретiн фракталдар теориясы.
Фрактал түсiнiгi алғаш математикалық түрде күрделi геометриялық,
формаларды сипаттау үшiн енгiзiлдi. Ғылымның дамуы және компьютерлiк
техниканы қолданудың алуан түрлi мүмкiндiктерi фрактал түсiнiгiнiң
табиғаттың ең жалпы, түбегейлi заңдылықтарымен байланысты екенiн көрсеттi.
Физика — математика ғылымдарының бұл жаңа бағытының күрт дамуына, француз
ғалымы Б. Мандельброттгың 1982 жылы жарық көрген, “Табиғаттың фракталдық
геометриясы” атты кiтабының шығуы тiкелей себеп болды. Мандельброт бұл
кiтабында табиғатта кездесетiн фракталдық нысандардың көптеген мысалдарын
келтiрдi және оған жаппай қызығушылық тұдырды. Оның дамытқан фракталдық.
геометриясы, сан түрлi обьектiлердің формасын сипаттауға қолданылуымен
қатар, кездейсоқ пайда болмайтын, масштабты —инварианты құрылымдардың
моделiн салуға мүмкiндiк бередi. Осы үлгiлердi қолдану ретсiз құрылымдарды
зерттеп бiлудің жаңа жолдары болып табылады.
Аспандағы бұлттар, тау сiлемдерi, терезе шынысына қатқан қыраулар,
полимердi түзетiн молекулалар, тiрi клеткалар мен тағы сол сияқты нысандар
мен құрылымдардың бәрiне ортақ бiр қасиеті, олардың кiшi және үлкен
бөлiктерiнiң бiр-бiрiне ұқсастығы. әртүрлі уақыт мезетiнде түсiрiлген,
үлкен және кiшi бұлттардың суреттерiн салыстыру, олардың өзгеру
заңдылығының бiрдей болатынын көрсетеді. Осы сияқты заңдылықты әртүрлі
масштабта түсірiлген жағалау сызықтарының фрагменттерін (мысалы, Британия
аралының, Арал теңiзiнiң, Балқаш көлiнiң) салыстыру арқылы да байқауға
болады.
Осындай өзұқсас нысандар үшiн француз математигi Б.Мандельброт жаңа —
фрактал (латыншадан аудармасы —бөлшектiк, кескiленген) ұғымын енгiздi. Ол
құрылымдық, өзiне-өзi ұқсас иерархиялық iшкi құрылысы бар объектiлердi
фракталдар деп атады. Фракталдық, қасиет бейсызық, процестер мен
құбылыстарды сипаттайтын фазалық кеңiстiктерде, күрделi жүйенiң
функцционалды харакеттерiнде, адрондардың әсерлесуiнде, қоғамның
экономикалық, көрсеткiштерiнiң өзгерiстерiнде және т.б. байқалады.
Фракталдардың дел және қатаң анықтамасы әзiрге жоқ. Б.Мандельброт алғаш
рет фрактал анықтамасының мынадай вариантын ұсынған: фрактал деп тұтас
күйiне белгiлi-бiр мағынада ұқсас бөлiктерден түратын құрылым айтылады.
Математикада өзұқсас геометриялық объектілер деп, бiрiне-бiрi ұқсас,
шектi бiрдей элементтерге бөлуге болатын денелер саналады. Мысалы, төменде
кесiндiнi, тең қабырғалы үшбұрышты, квадратты, кубты сәйкес 2, 4, 4, 8
өзұқсас элементтерге бөлу тәсілі келтiрiлген (1- сурет). Суреттен
фракталдың, қандай масштабта байқалғанына қарамастан, бiр-бiрiне ұқсас,
бiрдей түрге ие екендiгi бiлiнедi. Бірақ, қосымша еш информация алмай,
бiртiндегi кiшiрейiп немесе үлкейiп отыратын өзұқсас өркеш-өркеш бұлттардың
сыртқы пiшiнiнiн өлшемдерiн бағалау мүмкiн емес. Себебi, бұл кезде
элементтер саны өте көп және олар бiрсыңырғы орналаспайды. Бұл үшiн арнайы
өлшемдiлiк ұғымы енгiзiлуi тиiс.
1 —сурет.
Объектiнi өзұқсас элементтерге бөлу мысалдары.

2.1. Фракталдық өлшемдiлiк

Жалпы өлшемдiлiк ұғымы, кеңiстiктегi нүктенiң орнын анықтауға мүмкiндiк
беретiн, ең аз тәуелсiз координаталар санын анықтаумен тығыз байланысты.
Физикада бұл — геометриялық объектiнi бейнелеуге мүмкiндiк беретiн тәуелсiз
айнымалылар санымен — параметрлiк өлшемдiлiкпен сәйкес келедi. Евклид
кеңiстiгiндегi көлемдi анықтауға керектi бұндай айнымалылар саны үшке тең
(х, у, z), жазықтық өлшеуге оның екеуi (х, у) болса жеткiлiктi, ал сызық
үшiн бiр координата х болса да жарайды. Нүктенiң өлшемдiлiгi нөлге тең. Осы
жағынан, кеңiстiк үш өлшемдi, жазықтық екi өлшемдi, ал сызық бiр өлшемдi
деп айтылады, яғни, параметрлiк өлшемдiлiктің мәндерi бүтін сандар 0,1,2,3.
Өлшемдiлiктің екiншi түрiне топологиялық өлшемдiлiк d жатады.
Топологиялық. өлшемдiлiктің d былай берiледi: кез-келген жиының
топологиялық, өлшемдiлiгi, оны екi, өзара байланыссыз бөлiктерге ажырататын
киманың өлшемдiлiгiне, бiрдi қосқанға тең. Түзудi, екi байланыссыз
кесiндiлерге бөлу, оның бiр нүктесiн алып тастау арқылы жүзеге асырылады.
Ал шектi нүктелер жиынының өлшемдiлiгi нөлге тең болғандықтан, сызық бiр
өлшемдi, яғни dc=0+1. Жазықтық. екі өлшемдi, себебi, оны екiге бөлу,
өлшемдiлiгi бiрге тең, сызық арқылы ғана жүзеге асыруға болады, яғни,
dж=1+1. Көлемдiк, геометриялық өлшемдi, себебі, оны екіге бөлетiн
жазықтықтың өлшемдiлiгi екіге тең, яғни, dж=2+1. Осылардан, топологиялық
өлшемдiлiктер де d=0,1,2,3. бүтін сандар.
Бірақ, табиғатга кездесетiн кейбiр нысандарды өлшеу үшiн, бұл
өлшемдiлiктер жеткілiксiз болып шықты. Себебi, адамның сезiм мүшелерiнiң
қабылдау шегi, өлшеулердi шектi масштабтар диапазонында жүргiзуге мүмкiндiк
бередi. Әрине, бұл қабылдау шегiн, әртүрлi сезiмтал құралдар (микроскоптар,
телескоптар және т.б.) басқа деңгейге ауыстыруға болады, бірақ барлық
масштабты бiр мезгiлде қадағалау және нысандардың өлшемдерiнiң әртүрлi
масштабта қандай қатынастарда болатынын тағайындау қиын. Информациялық.
кордың молаюы мен гылыми—техникалық прогресс бұл қиындықты жеңуге мүмкiндiк
бердi.
Алғаш рет, күрделi нысандарды өлшеудi ағылшын физигi Л. Ричардсон
жүзеге асырды. Ол фракталдық құрылымдiрдың бәрiне ортақ маңызды
ерекшелiктерiнiң бiрi — олардың аддитивтiлiгiн, яғни, өлшенетiн шама
(ұзындық, аудан, көлем, масса, заряд және т.б.) мәндерiнiң кеңiстiкте
жүргiзiлген өлшеулердің дәлдiгiне тәуелдiлiгiн пайдаланды. Мысалы, аса
күрделi, шымшытырық броундық. бөлшектің ұзындығы L, өлшеу бiрлiгiне (
(масштабына) байланысты. Масштаб кiшiрейген сайын өлшенген ұзындық арта
бередi.
Л.Ричардсон Британия аралының әртүрлi масштабта түсiрiлген карталарын
алып, оның А және С нүктелерiнiң, арасын қосатын жағалау сызығының
ұзындығын анықтау үшiн, адымы ( - ға тең ашамен өлшеулер жүргiздi
(2—сурет). А Нүктесiнен С нүктесiне дейiн жүрiп өткендегi аша адымының
санын N(() бiлу арқылы Л.Ричардсон өлшенетін жағалау сызығының ұзындығын
мына өрнекпен анықтады:

(1)
Бұл кезде масштабтың ( iшiне кiретiн кiшi иiлулер, ойыстар, мен
дөңестер есептелмейтінi белгіл Ол ескеру, яғни, одшеу кателiгiн кемiту үшін
Л.Ричардсон, өлшеу масштабын кiшiрейтiп өлшеулердi қайталады. Ендi, бұрынғы
көптеген иiлулер, дөңестер есептелгендiктен, өлшенген ұзындық бiршама естi.
Сөйтiп ол, ашаның адымын үнемi кiшiрейтiп отыру, жағалау сызығының ұзаруына
әкелетiн, шексiз өзгертулер енгiзуге мүмкiндiк беретiнiн байкады. Сонымен,
айыру қабілеттілігін арттыру, яғни, өлшеу масштабын кемiту, әр кезде
күрделi сызықтардың ұзаруына әкеледi.

2—сурет.
Теңiз жағалауының фрагментi.
Фракталдық, нысандарды өлшеудің тағы бiр тәсілі — өлшенетiн нысанды
немесе оның фрагментiн, қабырғаларының ұзындығын ( - ға тең, квадрат
ұяшықтардан құралған торлармен жабу. Бұл кезде де өлшенетiн фракталдық
нысаыңы түгел жабатын ұяшықтар саны N(() есептеледi (3-сурет). Тежiрибелер,
жағалау сызығының фрагментiн жабатын, квадрат ұяшықтардың саны, жуық
шамамен, сол қашықтықты түгел ететiн аша адымының санына тең болатынын
керсеттi. Егер жағалау сызығы белгiлi L0 ұзындыққа ие болса, онда оны
жабатын квадрат ұяшықтардың саны өлшеу масштабына кері пропорционал
өзгередi. Сонда, (1) өрiнекпен есептелетін, жағалау С ұзындығы, (
кiшiрсйген сайын, түрақты L0 - ұмтылады.

3—сурет.
Картадағы жағалау сызығын ұяшықтарға бөлу.

Сонымен, Л.Ричардсон өлшеу масштабы кемiген сайын, фракталдық
объектiнiң (жағалау сызығының) өлшемi дәрежелiк заңм өсетiнiн тағайындады:

(2)
Мұндағы L0 - өлшенетiн объектiнiң бастапқы және соңғы нүктелерiн
қосатын түзудің ұзындығы.

Бұл өрнек Ричардсон заңы деп аталады. Дәрежелiк көрсеткiш ( терiс мәнге
ие болуы тиiс. Жағалау тормен өлшеу тәсілінде де, ( кемуi, торды түзетiн
квадрат ұяшықтардың санын көбейтетiн болғандықтан, Ричардсон заңы
орындалады:
(3)
А — қабырғаларының ұзындығы L0 квадраттың ауданы.
Өте кiшi масштабтарда “жағалау сызығы” ұғымының менi жоғалады. Ал
атомдар аралық қашықтықтарда “аша адымы”, “квадрат ұяшық” ұғымдары да өз
мәндерiн жоятыны түсiнiктi. Себебi, бұл кезде кванттық механиканың зерттеу
обылыстарына енемiз. Бірақ., қалай дегенмен, Ричардсон заңы кең масштабты
диапазонда орындалатыны дәлелдендi. Осыдан жоғарыда тағайындалған физикалық
заңдылықтың сипатын түсiну мен түсіндiрудің математикалық құралы болуы
тиiстiгi тындайды.
Бұл құралды табу үшiн кез—келген физикалық шаманы өлшеу процесiнiң
жалпы сатылары қарастырылады, себебi, жаңа дережелiк заңдар (2), (3) өлшеу
нәтижелерiне сүйенiп тағайындалған. Бiз, объектiнiң санақ жүйелерiнiң
өзгерiстерiне сәйкес түрақты сипаттамаларын, яғни, инвариантты
сипаттамаларын қарастырамыз. Объектiнiң инвариантты сипаттамаларының
аддитивтi (объектiнiң сипаттамасы оны құрайтын элементтердің
сипаттамаларының қосындысына тең) және скалярлы болатыны белгiлi. Жиындар
теориясында инвариантты, аддитивтi және скалярлы қасиеттерге ие
сипаттамалар өлшем деп аталады. Классикалық физикада объектiнiң өлшемi
ретiнде ұзындық аудан, көлем, заряд, масса, оларды жүзеге асыру ықтималдығы
және т.б. жатады.
Математиктер тегiс емес күрдслi объектiлердi бейнелеу үшiн бөлшектiк
(Хаусдорф-Безикович) өлшемдiлiгiн қолданады. Бұл өлшемдiлiктi анықтауда,
кеңiстiктегi нүктелердің ара қашықтығы, олардың таралу заңдылығы негiзгi
роль атқарады. Осы нүктелер жиынының өлшемдiлiгiн тағайындау үшiн өлшем
ұғымы енгiзiлген.
Өлшенетiн шаманы түгел жабатын кесiндiлердің, квадраттардың, кубтардың
санын бiлу, объектiнiң өлшемiн анықтауға мүмкiндiк бередi. Мысалы, қисық
сызықтың ұзындығы, оны түгел жабатын, масштабы ( түзу кесiндiлердің санын
N(() бiлу арқылы анықталады (4а-сурет). Кәдiмгi тегiс қисық үшін
,
ал оның ұзындығы, шекке көшу арқылы, мына формуламен анықталады:
(4)

((0 ұмтылғанда өлшем L асимптоталы түрде қисықтың ұзындығына теңеледi
және өлшеу масштабына ( тәуелсiз.

4—сурет.
ұзындықты, ауданды және көлемдi өлшеу әдiстерi.

Нүктелер жиынына жазықтықты сәйкестендiруге болады. Мысалы, қисықты
түгелдей жабатын квадраттардың санын бiлу арқылы, оның ауданын табуға
болады. Бұл кезде өлшем аудан. Егер осы қисықты жабатын квадраттардың саны
N((), ал әр квадраттың көлемi нөлге теңеледi.
Ауданы (2 - қа тең болса, қисықтың ауданы мынаған тең (46—сурет):

Бұнда ұмтылғанда ((0 ұмтылады. Яғни, қисықтың ауданы нөлге тең.
Дәл осы сияқты етiп, қисықтың көлемдiк өлшемiн қолдануға болады.
Бірақ, сызықтың көлемi болмайтыны түсiнiктi,

мұнда N ( ұмтылғанда ((0.
Ендi беттi түзетiн нүктелер жиынын қарастырайық және оның өлшемi
ретiнде ұзындық. алынсын. Бұл кезде
ал беттiң ұзындығы

мұнда Олай болса, аудандың сызықтар жиынымен жабу мүмкiн емес.
Сонда нүктелер жиыны бет құраса, оның өлшемi тек аудан болуы тиiс,
осыдан:
(5)
мұнда да Беттің өлшемi ретiнде көлем алып көрелiк. Бұл ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.