Ом заңы. Өткізіштердің кедергісі

Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 6 бет
Таңдаулыға:

Ом заңы. Өткізіштердің кедергісі

Омның тәжірибе жүзінде тағайындаған заңы бойынша біртекті металл өткізгіштің бойымен ағатын ток күші осы өткізгішке түсірілген U кернеуге пропорционал болады, яғни

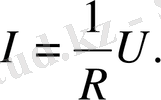(1)

Тосын күштер әсер етпейтін өткізгіш біртекті өткізгіш деп аталады. Бұл жағдайда, біздің байқауымызша, U кернеуі өткізгіштің ұштарындағы ϕ ₁ - ϕ ₂ потенциалдар айырымына тең болады. R шамасы өткізгіштің электрлік кедергісі деп аталады. Кедергінің бірлігіне кернеуі 1 в болғанда бойымен 1 а ток өтетін өткізгіштің кедергісіне тең шама ом алынады.

Гаусс системасында кедергінің бірлігі үшін, ұштарында потенциалдар айырмасы 1 СГСЭ бірлік болатын, ал өзімен 1 СГСЭ бірлік ток күші ағатын өткізгіштің кедергісі алынады. Ом мен кедергінің осы СГСЭ бірлігінің арасындағы байланысты табайық.

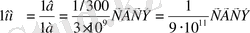кед. бір.

Олай болса

1 СГСЭкед. бір. =9 · 10 ¹¹ ом. . (2)

Өткізгіш кедергісі өткізгіштің материалына, өлшеміне және формасына байланысты. Біртекті цилиндр тәрізді өткізгіш үшін

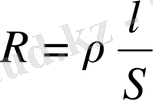(3)

мұндағы l - өткізгіштің үзындығы, S - оның көлденең қимасының ауданы, ρ - өткізгіштің меншікті электрлік кедергісі деп аталатын өткізгіштің меншікті электрлік кедергісі. Егер l = 1 және S =1 болса, онда R сан жағынан -ρ-ға тең болады. СИ системасында ρ ом-метрмен өлшенеді (ом∙м) . Практикада көбінесе l = 1 м және S =1 мм ² болғандағы кедергісі бар материал сипатталады, яғни ρ шамасы 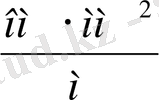өлшемімен өрнектеледі.

Ом заңын дифференциал түрінде жазуға болады. Ол үшін ойша өткізгіштің ішіндегі қандай да бір нүктенің аймағынан жасаушыларымен берілген нүктеде ток тығыздығының j векторына параллель болып келетін элементар цилиндрлік көлем алайық (1-сурет) . Цилиндрдің көлденең қимасы арқылы күші jdS шамасындағы ток өтеді. Цилиндрге түсірілген кернеу Edl шамасына тең мұндағы Е - берілген орындағы өріс кернеулігі. Соңында, (3) формуласы бойынша цилиндрдің кедергісі 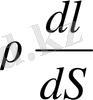ке тең. Осы мәндерді (1) формуласына қойсақ, онда

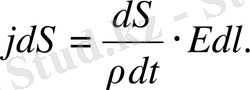
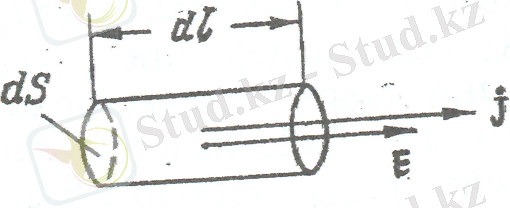
1 сурет

Әрбір нүктеде заряд тасушылар Е векторына бағыттас қозғалады. Сондықтан j және Е-нің бағыттары бірдей болады. Сөйтіп, былай жазуға болады:

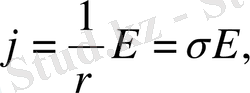(4)

мұндағы 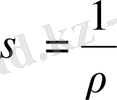шамасы электр өткізгіштің коэффициенті немесе материалдың өткізгіштігі деп аталады.

(4) өрнегі дифференциал түріндегі Ом заңын көрсетеді.

Ом заңы біртекті тізбек учаскесі үшін, яғни электр козғаушы күші әсер етпейтін тізбек үшін орынды. Біртекті емес тізбек учаскесіне арналған Ом заңының өрнегін алу үшін энергияның сақталу заңына сүйенеміз. Учаскенің ұштарындағы потенциалдар айырымы ϕ ₁ - ϕ ₂ болсын делік (2-сурет) . Учаскеге әсер ететін э. қ. күшін <§ _!2 деп белгілейік.

2-сурет,

Белгілі бір бағытта (2-суретте стрелкамен көрсетілген) ток пен э. қ күшін દ ₁₂ алгебралық шама ретінде қарастыруға болады. Стрелкамен бағыттас токты оң деп, ал оған қарама-қарсы токты теріс деп есептейміз. Осы сияқты стрелканың бағытымен бағыттас әсер ететін э. қ. күшті оң деп (бұл оң зарядтарды осы бағытта қозғайтын тосын күштер он жұмыс істейді деген сөз), ал қарама-қарсы әсер ететінді теріс деп есептейік.

Егер тізбектің учаскесін құратын өткізгіштер козғалмайтын болса, онда ток тек өткізгішті қыздыру нәтижесінен жүреді. Сондықтан зарядты тасымалдаушы барлық күштердін (электростатикалық және тосын күштер) істеген жұмысы бөлініп шыққан жылуға тең болады. dt уақыт ішінде өткізгішпен dq==Idt заряд өтеді. Сонда өрнегі бойынша осы зарядты тасымалдауға кеткен жұмыс мынаған тең:

dA = દ _l2 dq+ (ϕ ₁ - ϕ ₂ ) dq.

dt уақыт аралығында бөлініп шыққан жылу:

dQ = I ² Rdt= IR(Idt) =IRdq.

Осы екі өрнекті теңестіріп және dq-re қысқартып, мынаны аламыз:

IR= (ϕ ₁ - ϕ ₂ ) + દ ₁₂ , (5)

Осыдан

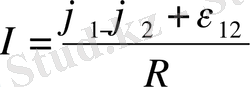(6)

(5) және (6) формулалары тізбектің біртекті емес учаскесіне арналған Ом заңын өрнектейді.

Тізбектің тармақталуы. Кирхгоф заңы

Егер Кирхгоф тұжырымдаған ережелерді пайдалансақ, онда тармақталған тізбектерді есептеу едәуір жеңілденеді. Мұндай заң екеу. Осылардың біріншісі тізбек түйініне арналған. Түйін деп екіден көп өткізгіштер жинақталатын нүктені айтады (3-сурет) .

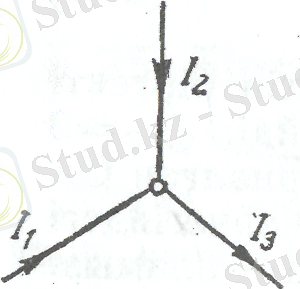
3-сурет

Түйінге қарай аққан токты бір таңбалы (плюс немесе минус), ал түйіннен шығатын токты басқа таңбалы (минус немесе плюс) деп санаймыз. Қирхгофтың бірінші заңы былай делінеді, түйінде жинақталатын ток күштерінің алгебралық қосындысы нольге тең:

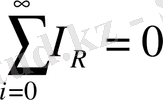(7)

Бұл қағиданың дұрыс екенін мынадай пайымдаудан байқауға болады. Егер түйіндегі токтардың алгебралық қосындысы нольден өзгеше болса, түйінде зарядтар көбейіп не азайып кетер еді де, бұл өз кезегінде түйіндегі потенциалдың және тізбекте ағатын токтың өзгеруіне әкеп соғар еді. Сөйтіп, тізбектегі ток тұрақты болу үшін (7) теңдеудің шарты орындалуы керек екен.

(4) теңдеуді тізбектің әрбір N түйіні үшін жазуға болады. Алайда тәуелсіз тек N -1 теңдеуі ғана, ал N-шi осылардың салдары болып табылады.

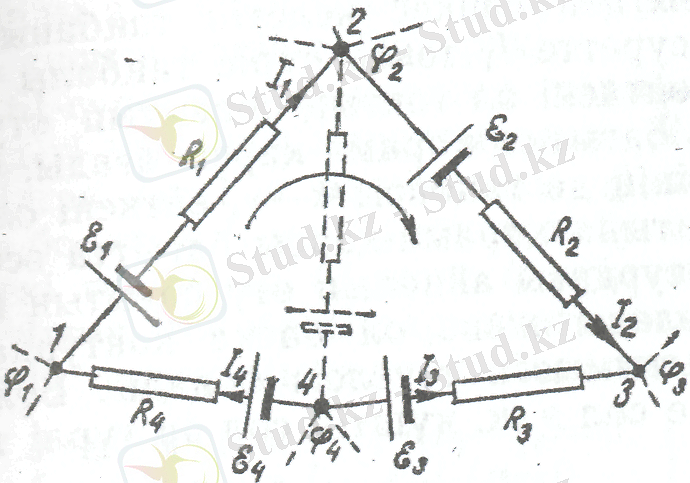
4 сурет

Ойша тармақталған тізбектен қалауымызша бір тұйық контур бөліп алайық (4-суреттегі 1 - 2 - 3 - 4 - 1 контурды қараңыздар) . Орағыту (бір айналып шығу) бағытын алып (мысалы, суретте көрсетілгендей, сағат тілінің оң бағыты) және контурдың әрбір тармақталмаған учаскелеріне Ом заңын пайдаланамыз, яғни

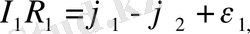
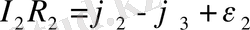
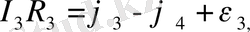
Осы өрнектерді қосқанда потенциалдар қысқарады да мынадай тендеуді аламыз:

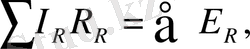(8)

бұл Кирхгофтың екінші ережесін анықтайды.

(8) теңдеуі берілген тармақталған тізбектен, ойша бөліп алған барлық тұйық контурлар үшін құрылуы мүмкін. Бірақ тәуелсіз теңдеулерді басқа контурларды бір-бірімен беттестіру арқылы алуға болмайтын контурлар үшін ғана құруға болады. Мысалы, 5-суретте кескінделген тізбек үшін үш теңдеу құруға болады.

1) бірінші контур үшін 1-2-3 - 6-1,

2) екінші контур үшін 3-4-5-6-3,

3) үшінші контур үшін 1 - 2 - 3 - 4 -5- 6 - 1.

Соңғы контур бірінші екеуін беттестіруден алынады. Демек, көрсетілген теңдеу тәуелсіз болмайды. Тәуелсіз теңдеулер қатарына үш теңдеудің екеуін алсақ болады.

Кирхгофтың екінші ережесінің теңдеуін құрғанда ток пен э. қ. күшіне токтың айналып өтуіндегі таңдап алынған бағытпен сәйкес келетін таңбаны есептейміз. Мысалы, 5 суретте I ₁ токты теріс таңбалы деп есептеуіміз керек, өйткене ол тоқтың орағытып өтуіндегі таңдап алынған бағытка қарама-қарсы ағады. Сол сияқта દ ₁ э. қ. күшінің де таңбасы «-», өйткене ол да токтың орағыту бағытына қарама-қарсы бағытта әсер етеді.

Әрбір контурдағы айналып өту бағатын қалауымызша алуға болады және ол басқа контурдағы таңдап алынған бағытымызға тәуелсіз болады. Бұл жағдайда тоқтың немесе сол э. қ. күштің сол әр түрлі теңдеулерге

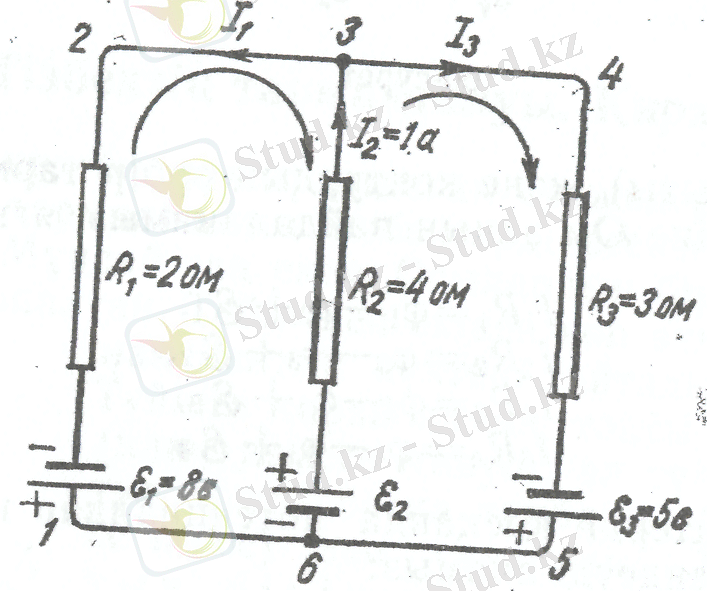
5 сурет

әр түрлі таңбалармен қатысуы мүмкін (мысалы, 5-суретте контурларда көрсетілген орағыту бағытымен өткен I ₂ ток осындай) . Алайда мұның ешбір мәні болмайды, өйткені орағыту бағытының өзгеруі (8) теңдеуде барлық таңбаның кері бағытқа өзгеруіне әкеліп соғады.

Теңдеуді құра отырып, тізбектің тармақталған учаскесінің кез келген көлденең қимасынан бірдей ток өтетінін есте ұстаған жөн.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.