Компьютерлік корреляциялық талдау және эксперименттік деректерді статистикалық өңдеу


Компьютерде корреляциялық талдау мәселелері
М А 3 М Ұ Н Ы
КІРІСПЕ . . . … . . . 3
ТАРАУ I. Өлшеу қателері . . . …. 4
§1. Өлшеу қателерін классификациялау . . . …. . 6
§2. Сандардың жуытауы және олардың абсолюттік және салыстырмалы қателіктері . . . 7 Өлшеудің кездейсоқ қателерінің таралуы . . . . 10
§4. Өлшеу дәлдігінің көрсеткіштері . . . …. . 10
ТАРАУ ІІ. Орта мәндер (және олардың қателері) . . . …. . 10
§1. Орта мәндер . . . …. . 12
§2. Теориялық орташа . . . … . . . 14
§3. Өлшейтін шаманың дәлмәнінің бағасы . . . ……15
§4. Өлшеу дәлдігін бағалау . . . …. . 17
ТАРАУ III. Ең кіші квадраттар әдісі . . . … . . . 17
§1. Есептің қойылуы . . . … . . . 19
§2. Ең кіші квадраттар әдісінің қойылуы . . . …. . 21
§3. Параметрлер арасындағы байланысты табу . . . … . . . 24
§4. Эмпирикалық берілгендерді тегістеу . . . …. 27
ТАРАУ IV. Коррелециялық байланыс . . . …. . 28
§1. Сызықтық коррелеция . . . … . . . 35
§2. Сызықтық емес коррелеция . . . … . . . 36
§3. Көптік коррелеция . . . … . . . 40
ТАРАУ V. Эксперименттік берілгендерді компьютерде өңдеу . . . 41
ӘДЕБИЕТТЕР . . . 42
ПРОГРАММАЛАР . . . , . . . 42
- Кіріспе
Қазіргі кезде математикалық статистика ауыл шаруашылығында, өндірісте, химия, физика, биология, медицина, метеорология, гидротехника, мелиорация, лингвистика және т. б. салаларда қолданылады.
Математикалық статистика сызықтық программалаудың көптеген есептерін шешуге мүмкіндік береді.
Математикалық өндеу және эксперимент нәтижелерін анализдеу жоғарғы оқу орындарының студенттеріне, дипломниктеріне, аспиранттарына және т. б. керекті мәліметтер құрамына тереңдеп еніп келеді. Педагогикалық жоғарғы оқу орындарының программасында эксперименттік берілгендерді статистикалық өңдеу әдістері толық көлемде оқылмайды, яғни педагогикалық оқу орындарының программасында жеке "Математикалық статистика" және "Корреляциялық анализ" оқулығы жоқ.
Сондықтан нәтижелерді өңдеу, әдістері жөніндегі білімінің аздығынан педагогикалық жоғарғы оқу орындарының студенттеріне эксперимент санының көп болуы, біршама қиындықтуғызады.
Осы мақсатқа байланысты беріліп отырған жұмыстың міндеті мыналар болып табылады :
1. Корреляциялық талдау әдісін және математикалық статистика әдістерін оқып білу.
2. Осы әдістерді қолдана отырып, әр түрлі факторлардың арасындағы корреляциялық байланысын табу.
3. Байланыс түрлеріне байланысты программа құру және сол программалардың көмегімен нәтижелерге талдау жүргізу керек.
- Өлшеу қателері
Күнделікті өмірде пайдаланылатын көптеген шамалардың сандық мәні оны өлшеу нәтижесінде шығады, яғни тура сондай бірлік деп есептелетін басқа шамамен оны салыстыру арқылы алынады. Еш қандай физикалық шама абсолютті дәлдіктегідей белгілі емес. Сол сияқты өлшеу кезінде кететін қателер болады.
Өлшеу қатесі деп өлшенетін шаманың өлшеу нәтижесі х пен шын мәні а арасындағы айырмашылықты, яғни х-а айтады.
Өлшеу қатесі, өлшенетін шаманың шын мәні сияқты белгісіз болады. Эксперимент нәтижелерін математикалық өндеудің негізгі есебінің бірі, алынған нәтижелер бойынша, өлшенетін шаманың дәл мәнін бағалау болып табылады. Басқаша айтқанда, бірнеше рет шаманы өлшегеннен және нәтижелер қатарын алғаннан кейін, бұлардың әрбіреуінің белгісіз қателері болады, мүмкіндігінше, аз қатесімен жуық мәнін табу есебі қойылады.
Бұл есепті шешу үшін өлшеу қатесінің негізгі қасиеттерін білу керек және оларды қолдана білу керек.
Өлшеу қатесін классификациялау
Өлшеу жүргізген кезде әртүрлі қателер кетеді. Олар мыналарға бөлінеді:
1. Систематикалық қате
2. Оғаш қате
3. Кездейсоқ қате
1. Систематикалық қате дегеніміз бірқалыпты жағдайда тәжірибені қайталағанда анықталмайтын қателерді айтамыз. Олар көптеген әртүрлі себептерден болады. Мысалға, прибордың жетіспеушілігінен (приборлық систематикалық қателер, олар прибор дәлдігінің класымен анықталады), сыртқы ортаның әсерінен, экспериментшінің дұрыс жасамағанынан, нәтиже дәл мәнінен өзгеріп кетуінен болады. Оларды арнайы өлшеу жүргізу арқылы анықтауға және өлшеу нәтижесіне лайықты түзету енгізу жолымен жойып жіберуге болады. (Мысалға, белгілі шаманы әртүрлі методпен өлшеу немесе бір прибормен түрлі эталондарды өлшеу) .
2. Огаш қате. Олар өлшеудің негізгі шарттарын бұзу нәтижесінде немесе экспериментшінің байқамай қате жіберуінің нәтижесінен пайда болады. (Мысалға, "3"-тің дұрыс көрінбеуінен, оның орнына "8" жазып қою) . Нәтижелерде өңдеу кеткенін байқап қалған жағдайда өлшеу нәтижесін тастап, егер мүмкіндік болса қайталап шығу керек. Оғаш қатесі бар нәтиженің сыртқы белгісі, оның негізгі өлшеу нәтижелерінен кенеттен оғаш асып немесе кеміп кетуі.
3. Кездейсоқ қате деп барлықсистематикалық қателерді жойғаннан кейін қалған өлшеу қателерін, яғни нәтижелерді өлшегенде лайықты түзету енгізу жолымен түзетілген қателерді айтамыз. Олар мұндай факторлардың көпшілігіне, өте көп емес, тіптен оларды бөліпалуға болмайтындай және жекелей есепке ала бермейтіндей қимыл эффектісін туғызады.
Кездейсоқ қатені мұндай факторлардың қимыл эффектілерінің жиынтығы түрінде қарастыруға болады. Олар жойылмайтын болып табылады. Оларды әрбір өлшеу нәтижелерінде жоюға болмайды. Бірақ ықтималдықтар теориясының методтарының көмегімен олардың, өлшенетін шаманың дәл мәнінің бағасына әсер етуін есепке алуға болады, өлшенетін шама мәнін барынша аз қатемен анықтауға мүмкіндік береді.
2. 2. Сандардың жуықтауы, олардың абсолюттік және салыстырмалы қателіктері.
Есептеу шаманың жуық мәндерімен, яғни жуық сандармен заңды түрде жүргізіледі. Есептеу үшін бастапқы берілгендердің кейбір қателіктері әлдеқашан беріледі, есептеу барысында жуықтаудан, жуық формулаларды қолданудан тағы да қателіктер жиналады.
а жуық санының қателігі деп, яғни а жуық санымен дәл мәні а 0 -ң арасындағы айырымы, әдеттегідей белгісіз.
а жуық санының бағалауының қателігі деп мына түрдегі теңсіздікті түсінеді:
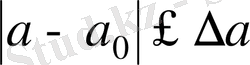 (2. 1)
(2. 1)
∆a санын а жуық санының абсолютгік қателігі деп атайды. Абсолюттік қателік 2-3-тен кем емес мәнді цифрмен жазу келісілген (мәнді цифрларды санау кезінде 0-дер саналмайды) .
Жуық а санының салыстырмалы қателігі деп оның да абсолютті қателігінің жуық а санының абсолют шамасына қатынасын айтады, яғни:
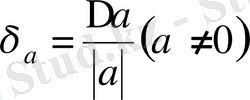 (2. 2)
(2. 2)
Салыстырмалы қателік кіші сан болатындықтан, ол әдетте процентпен көрсетіледі. Жуық санның салыстырмалы қателігі оның сенімді белгілерінің санына байланысты.
Санның сенімді белгілерінің саны санның бірінші мәнді цифрына дейін саналады, мысалға, ∆S=0. 0926 абсолютті қателігі болатын S =20. 7426 санының үш сенімді белгісі бар (2, 0, 7), қалғандары сенімсіз. Бір сенімді белгі болса, салыстырмалы қателік 10% (δ=10%), егер екі сенімді белгісі болса, онда 1% (δ=1%) ретті қателік, ал үш сенімді белгісі болса, онда 0, 1% (δ=0, 1%) ретті қателік және т. с. с. болады.
2. 3. Өлшеудің кездейсоқ қателерінің таралуы.
1. Ықтималдық моделі
Өлшеудің кездейсоқ қателері олардың таралуының белгілі бір заңы бойынша сипатталады. Мұндай заңның бар екенін мынадан байқауға болады; өзгермейтін ортада өлшеуді бірнеше рет қайтара жасағанда, кез-келген бөлінген интервалда болатын кейбір m шамалары, өлшеуді барынша үлкен сан болатындай етіп жүргізгенде осы m санының жалпы сан "n"-ге қатынасы тұрақты бір санға жақын болуы мүмкін. Бұл жағдай өлшеудің кездейсоқ қателерін зерттеуде ықтималдықтар теориясының методтарын қолдануға мүмкіндік береді. Ықтималдықтар теориясы моделдерінде кездейсоқ қателіктер z=х-а, кез келген мәнді қабылдайтын, сол сияқты кез келген интервалға (z 1 , z 2 ) интервалға кездейсоқ z шамасының дәл түсуі (тура санның болуы) ықтималдығы деп аталатын, толық белгілі бір сан сәйкес келетін, кездейсоқ шама ретінде қарастырылады және оны былай белгілейді P=(z 1 <z>z 2 ) .
Кез келген интервал үшін (z 1 , z 2 ) ықтималдықты P=(z 1 <z>z 2 ) табуға мүмкіндік беретін ереже z кездейсоқ шаманың ықтималдығының таралу заңы деп атайды. Ол мына интервалдың көмегімен жазылады:
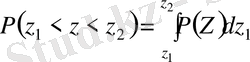 (2, 3)
(2, 3)
мұндағы:
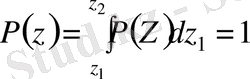 (2, 4)
(2, 4)
шартымен нормаландырылған аталатын кейбір функция.
2. Таралудың қарапайым заңы
Өлшеудің кездейсоқ қателерінің таралу заңы ретінде таралудың қарапайым заңы жиі қолданылады. Қарапайым таралудың тығыздығы мынаған тең:
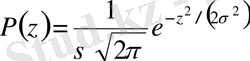 (2. 5)
(2. 5)
мұндағы
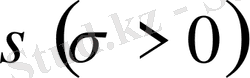 параметрі өлшеудің дәлдігін сипаттайды. Ықтималдықтың таралуының тығыздығының графигі таралу қисығы деп аталады.
параметрі өлшеудің дәлдігін сипаттайды. Ықтималдықтың таралуының тығыздығының графигі таралу қисығы деп аталады.
Сурретте σ-ң әр түрлі мәндеріндегі қарапайым таралу қисықтары көрсетілген. Бұл суретте қарапайым таралу қисығы σ параметріне байланысты OZ осінің бойымен сығылады және Р(Z) өсінің бойымен созылады, сол сияқты σ кішірейген сайын, Р(Z) таралу тығыздығы соншалықты өсуімен кемитіндігі көруге болады.
(2. 3) таралу заңының Z 1 , Z 2 интервалында болу ықтималдығын графиктік түрде көрсетсек ықтималдықтың таралуының қисығындағы сәйкес қисық сызықты трапецияның ауданымен көрсетіледі.
а) Қарапайым таралуда кездейсоқ шаманың (-2, 2) қарама-қарсы интервалда болу ықтималдығы мына формуламен өрнектеледі:
Р(-z 1 <z<z 1 ) =Р(z< z 1 ) =2Ф(z/σ)
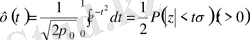 (2. 6)
(2. 6)
Мұндағы Ф(t) ықтималдық интегралы
б) Қарапайым таралуда кездейсоқ қатенің кез-келген интервалға түсу ықтимадығы мына формуламен өрнектеледі:
Р(-z 1 <z<z 2 ) =Ф(z 2 /σ) -Ф(z 1 /σ) (2. 7)
Егер Z кездейсоқ қатесі (2. 5) тығыздық пен таралуының қарапайым заңына тез болса, онда өлшеу нәтижелерінің таралуы х=а+z тек а шамасына жақындалуымен (2. 5) тығыздықтан айырмашылығы болатын, мына тығыздыққа тең болады:
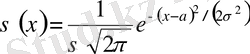 (2. 8)
(2. 8)
Таралудың бұл заңы а центрлі жалпы қарапайым таралу заңы деп аталады. Кездейсоқ шамалар үшін, олардың таралуының центрі 0-ге тең деп үйғарылады.
2. 4. Өлшеу дәлдігінің көрсеткіштері
1. Өлшеудің орта квадраттық қатесінің а параметрлері стандартты қате деп аталады.
2. а шамасының квадраты қатенің дисперсиясы деп аталады.
§3. Орта мәндер және олардың қателері.
3. 1. Орта мәндер
1. х 1 , х 2 , . . . , х n , шамаларының орта арифметикалық мәні (немесе жай ғана орта мәні) деп мынаны айтады:
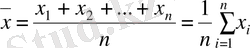 (3. 1)
(3. 1)
2. х
1
, х
2
, . . . , х
n
шамаларының олардың
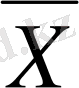 орта мәндерінен S орта квадраттық ауытқуы деп мынаны айтамыз.
орта мәндерінен S орта квадраттық ауытқуы деп мынаны айтамыз.
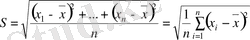 (3. 2)
(3. 2)
Кез-келген с санынан кезкелген орта квадраттық ауытқуды есептеуде мына формула қолданылады:
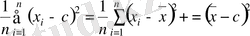 (3. 3)
(3. 3)
Егер өлшеу нәтижелерінің ішінде бір-біріне теңдері кездессе, онда (3. 1) және (3. 2) формулаларындағы ұқсас қосылатындарын біріктіруге болады. Мысалға, х і мәні М і рет кездескен болсын, х к мәні М к кездескен болсын, т. с. с., х к мәні М к рет кездескен болса (М 1 +М 2 + . . . +М к =n), онда (3. 1) және (3. 2) формулалары мына түрге келеді
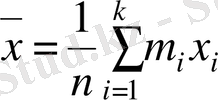 (3. 4)
(3. 4)
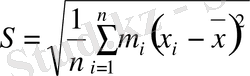 (3. 5)
(3. 5)
3. Өлшенген орта мәндер мына формуламен анықталады:
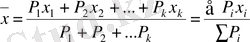 (3. 6)
(3. 6)
4. Өлшенген орта квадратты ауытқу мына формуламен анықталады:
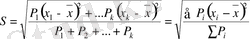 (3. 7)
(3. 7)
мұндағы P 1 , P 2 , . . . , P n ; х 1 , x 2 , . . . , х n өлшеулерінің сәйкесінше салмағы.
Егер есептеу басы қолайлы таңдалып, x i мәнін есептеуді лайықты масштабта жүргізсек, онда орта мәнді есептеу оңайланады. Практикада бұл сызықтың орын ауыстыруға әкеледі:
X i = c + hu i (i=1, 2, …, k) (3. 8)
Көрсетілген орын ауыстыруда есептеу формулалары мына түрге келеді:
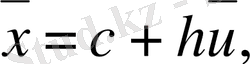
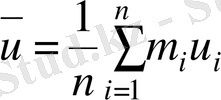 (3. 9)
(3. 9)
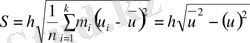 (3. 10)
(3. 10)
мұндағы:
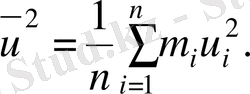
Тексеру үшін шығарылған салмақты есептеу басқа санақ басынан с 1 қайталанады, сонда нәтижелері мүмкін болған қателерді дөңгелектегендегі дәлдікпен тура келуі керек.
3. 2. Теориялық орташа
(Таралу моменттері)
Ықтималдар теориясы моделінде х 1 , х 2 , . . . , х n өлшеу нәтижелерінің әрбіреуі кейбір X кездейсоқ шамаларының мәндері сияқты болады. Мұндай түсінік беруде (3. 1) және (3. 4) орта мәндер х шамасының теориялық орташа математикалық күтуінің жуық мәні ретінде болады. х шамасының М х -пен белгіленеді және мына формуламен анықталады:
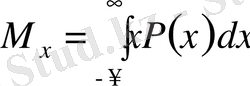 (3. 11)
(3. 11)
мұндағы Р(х) - х шамасының ықтималдығының таралуының тығыздығы.
F(х) функциясының х шамасынан математикалық күтуі мына формуламен анықталады:
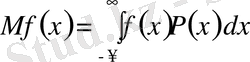 (3. 12)
(3. 12)
k ретінің бастапқы моментінің k-шы дәрежелі кездейсоқ шама деп аталады.
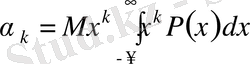 (3. 13)
(3. 13)
α
1
1-ші реттің бастапқы моменті сол х шамасының математикалық күту болып табылады. Ол х шамасының таралу центрі деп аталады. (2. 5) қарапайым таралу үшін таралу центрі 0-ге тең, ал (2. 8) жалпы таралу үшін таралу центрі

 айырымы (кездейсоқ шаманың центрінен ауытқуы) центрленген кездейсоқ шама деп аталады.
айырымы (кездейсоқ шаманың центрінен ауытқуы) центрленген кездейсоқ шама деп аталады.
k ретті орталық момент деп оның центрінен х шамасының ауытқығандағы математикалық күтуін айтады.
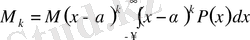
1-ші реттің орталық моменті әрқашан 0-ге тең: M 1 =0
2-ші реттің орталық моменті х шамасының дисперсиясы деп аталады және былай жазылады:
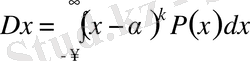 (3. 15)
(3. 15)
(2. 5) қарапайым және (2. 8) жалпы таралу үшін дисперсия
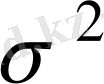 - қа тең. Дисперсиядан алынған квадрат түбір кездейсоқ шамасының орта квадраттық ауытқуы деп аталады және
- қа тең. Дисперсиядан алынған квадрат түбір кездейсоқ шамасының орта квадраттық ауытқуы деп аталады және
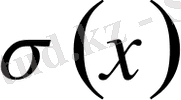 пен белгіленеді. Дисперсия және орта квадраттық ауытқуы х кездейсоқ шамасының таралуының сипаттау үшін қолданылады.
пен белгіленеді. Дисперсия және орта квадраттық ауытқуы х кездейсоқ шамасының таралуының сипаттау үшін қолданылады.
3. 3. Өлшенетін шаманың дәл мәнінің бағалары.
Кейбір шамалардың n-ге байланыссыз өлшеулерінің х нәтижесі берілсін. Бұл нәтижелер х 1 , х 2 , . . . , х n болсын және олар оғаш және систематикалық қателерден тазартылған болсын деп ұйғарайы.
Өлшенетін шаманың дәл мәнін бағалау дегеніміз:
а) а мәніне барынша өте жақын болатын (мұндай функция нүктелік бағалау деп аталады) мынадай функцияны өлшеу нәтижелерінен көрсету керек;
б) Р берілген ықтимадықтан а дәл мәнін жабатын (мұндай басалау сендіретін бағалау деп аталады) шекарасын көрсету керек.
а дәл мәніне өте жақын болу үшін, g(х 1, х 2 , . . . , х n ) бағалауы төмендегі қатыстарды қанағаттандыруы керек.
1. Араласпаушылық бағалау.
Егер оның теориялық орта мәні (математикалық күтуі) а дәл мәніне сәйкес келсе: М g =а
2. Өзбетіншілік бағалау.
Егер n өлшеу санын шектеп тыс көбейткенде, ол а дәл мәніне ықтимал ұмтылса: (g (n→∞a) ) n онда өзбетіншілік бағалау деп аталады.
3. Эффектілі бағалау.
Егер араласпаған бағалау өлшеу нәтижелері бойынша а мәнінің барлық араласпаған бағалауларының ішіндегі ең кіші таралуға тең болатын болса, онда оны эффектілі бағалау деп атайды.
Егер а шамасының барлық n өлшеулері бірдей дәлдікпен жүргізілген болса, (тең нүктелік өлшеу) онда өлшеу шамасының дәл мәнін бағалаудың орнына өлшеу нәтижелерінің орта мәндері қолданылады.
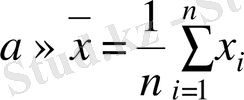 (3. 16)
(3. 16)
Бұл бағалау араласпаған және өзбетіншілік бағалау болып табылады. Қосымша ұйғарым бойынша, бұл өлшеулерді кездейсоқ қателері ықтималдықтардың таралуының қарапайым заңына бағынса, онда эффектілі бағалау болып табылады.
Егер өлшеу тең нүктелік болмаса, бірақ өлшеу салмаф: белгілі болса, яғни Р
1,
Р
2
, . . . , Р
n
сандары,
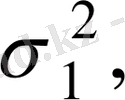
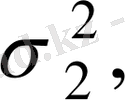
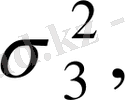 …,
…,
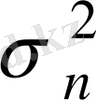 қателер дисперсиясына кері пропорционал болса,
қателер дисперсиясына кері пропорционал болса,
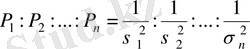
онда өлшенетін шаманың а дәл мәнінің бағасы ретінде өлшенген орта мән қолданылады.
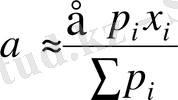 (3. 17)
(3. 17)
Бұл бағалау (3. 16) бағалауының барлық қасиеттеріне бағынады.
3. 4. Өлшеу дәлдігін бағалау.
Өлшеу қателері кездейсо қате болсын деп және қарапайым заң бойынша таралған деп ұйғарайық. Өлшеу дәлдігінің көрсеткіші ретінде сол заңның дисперсиясын
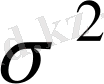 немесе орта квадраттық қатені
немесе орта квадраттық қатені
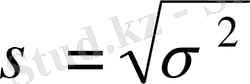 бағалайды.
бағалайды.
1. Егер белгілі шамаға (эталонға) өлшеу жүргізілсе, онда дисперсияның бағалауының орнына а мәні х 1 , х 2 , . . . , х n өлшеу нәтижелерінің а дәл мәнінен ауытқуларының орта квадратын қолданады:
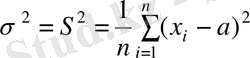 (3. 18)
(3. 18)
2. Егер белгісіз шаманы өлшесек, онда дисперсияны бағалауы ретінде эмпирикалық дисперсияны қолданамыз:
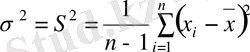 (3. 19)
(3. 19)
3. Егер бір құралмен m сериялы өлшеу жүргізсек онда дисперсияның бағалауы ретінде эмпирикалық дисперсиядан өлшенген орташаны қолданамыз:
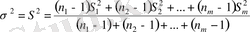 (3. 20)
(3. 20)
мұндағы n
1
, n
2
, n
3
, …, n
m
- cериядағы өлшеу саны.
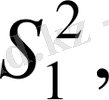
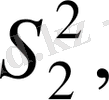
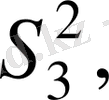 …,
…,
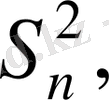 сәйкес эмпирикалық дисперсиялар.
сәйкес эмпирикалық дисперсиялар.
Әрбір сериядағы өлшеу саны бірдей болғанда,
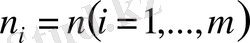 (3. 20)
(3. 20)
бағалауы мына түрге келеді:
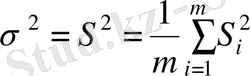 (3. 21)
(3. 21)
яғни мұнда дисперсияның бағалауы ретінде эмпирикалық дисперсияның орта квадраттық мәні қолданылады.
4. Бір ғана шаманың m сериялы өлшеуі үшін, тек n 1, n 2 , . . п m өлшеулер саны және әр сериядағы орташа нәтижелер белгілі болса, дисперсияның бағалауы ретінде орташалардың эмпирикалық дисперсиясын қолданамыз:
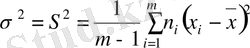 (3. 22)
(3. 22)
мұндағы
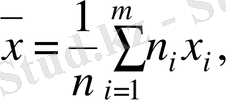
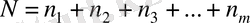
Бұл бағалау араласпаған және өзбетіншілік бағалау болып табылады (сол сияқты
 болғанда эффектілі бағалау болады) .
болғанда эффектілі бағалау болады) .
§ 4. Ең кіші квадраттар әдісі.
4. 1. Есептің қойылуы .
Бір у шамасының басқа бір х шамасымен функционалдық байланысын зерттеп білуде х шамасының әртүрлі мәндеріндегі у шамасын өлшеу қатарын құру керек.
Нәтижелер таблица немесе график түрде берілсін:
y
2-сурет 3-сурет
Есеп ізделінді функционаддық байланыстың аналитикалық көрсетуімен аяқгалады, яғни эксперимент нәтижелерін сипаттайтын формулаларды таңдаумен аяқгалады. Есептің негізгі мақсаты мынаған байланысты, өлшеудің кездейсоқ қателерінің бар болуы, тәжірибенің барлық мәндерін тура көрсететін, мұндай формуланы тандауды қисынсыз етеді. Басқаша айтканда, 3-суреттегі ізделінді функцияның графигі барлық нүктелер арқылы өтуі міндетті емес, ал мүмкіндігінше "шуды" тегістеу керек.
"Шуды" тегістеу жүргізілген эксперименттердің санының көп болуына байланысты нақгы және қолайлы болады, яғни соған қарай бізде көп информация аламыз. Мысалға, у=ах+b түзуін жүргізу үшін екі нүктенің (х 1, у 1 ) және (х 2 , у 2 ) белгілі болуы жеткілікті. Бірақ 4-суреттегідей өте "шудың" көп немесе аз болуында, осы мақсатта оншақгы нүкгелер керек болуы мүмкін. Әдетте эмпирикалық формуланы белгілі бір типтегі формуладан тандап алады. Мысалға,
y
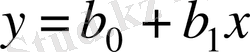
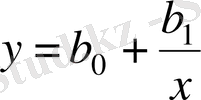
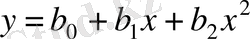
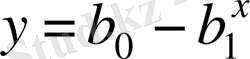
x
4-сурет
Басқаша айтқанда, есеп белгілі бір формуладағы b 0 , b 1 , b 2 , параметрлеріне табуға әкеледі осы.
Таңдап алынған функционалдық байланыста табуға болатын айқын нұсқауларымен барлық параметрлерді белгілейміз.
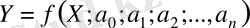 (4. 1)
(4. 1)
Бұл а 0 ; а 1 ; а 2 ; . . . а n параметрлерді, соңғыларының кездейсоқ қателерінің болуы мүмкін болғандықтан, у 1 , у 2 ; . . . у n функцияларының эксперименттік мәндерімен дәл анықтауға болмайды. Ең кіші квадраттар әдісі барлық а 0 ; а 1 ; а 2 ; . . . , а n параметрлерінің араласпаған және өзбетіншілік бағалауын табуға мүмкіндік береді. Бұл параметрлер (4. 1) сызықтық байланыстың формуласына енген болса, ең кіші квадраттар әдісі бойынша алынған параметрлердің бағалаулары, сол сияқты эффектілі бағалау болады. Бұл өте сирек кездесетін жағдай. Мұнда өлшеу қателері ықтималдықтардың таралуының қарапайым заңына бағынатындай етіп, у 1 , у 2 ; . . . у n функцияларының мәндерін өлшеуді бір-бірінен байланыссыз жүргізіледі.
4. 2. Ең кіші квадраттар әдісінің қойылуы.
1. Егер у 1 , у 2 ; . . . , у n функцияларының мәндерінің барлық өлшеулері бірдей дәлдікпен жүргізілген болса, онда а 0 ; а 1 , а 2 ; . . . а n параметрлерін бағалау мына шарттан анықталады:
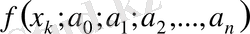 есептеулерінен y
k
өлшенген мәннің ауытқуының квадратының қосындысы, яғни,
есептеулерінен y
k
өлшенген мәннің ауытқуының квадратының қосындысы, яғни,
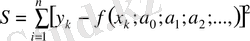 (4. 2)
(4. 2)
шамасы ең кіші мәні қабылдау керек.
2. Егер өлшеулер әртүрлі дисперсиямен (тең нүктелік емес) жүргізілген болса, онда жоғарыда көрсетілген шарт бойынша (4. 2) қосынды (4. 3) қосындысымен айырбасталынады:
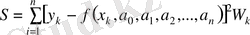 (4. 3)
(4. 3)
мұндағы, өлшеу салмағы деп аталатын дисперсияға кері пропорционал:
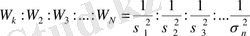
1. Егер функция мәндерінің барлық өлшеулері бірдей дәлдікпен жүргізілген болса, бірақ x k аргументінің әрбір мәнінде m k өлшеу жүргізілсе, ал
у
k
ретінде сериядағы орташа нәтижелер алынса, онда өлшеудің салмағы ретінде сериядағы өлшеу саны қолданылуы мүмкін.
 (k=1, 2, . . . , N) бұл шарт сондай-ақбірнеше айнымалысы бар функцияның параметрлерін бағалауды анықтауда сақталады. Мысалға, х, у екі айнымалысы бар Z функциясы үшін а
0
; а
1
, а
2
; . . . а
n
қосындының минимумға шартынан анықталады:
(k=1, 2, . . . , N) бұл шарт сондай-ақбірнеше айнымалысы бар функцияның параметрлерін бағалауды анықтауда сақталады. Мысалға, х, у екі айнымалысы бар Z функциясы үшін а
0
; а
1
, а
2
; . . . а
n
қосындының минимумға шартынан анықталады:
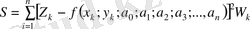 (4. 4)
(4. 4)
а 0 ; а 1 , а 2 ; . . . а n параметрлерін S функцияға қойғанда ең кіші мән беретін параметрлерін іздеу S=S(а 0 ; а 1 , . . . , а n ) арқылы құрылған мына n тендеулер системасын шешуге әкеп соғады:
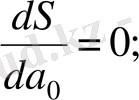
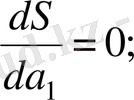
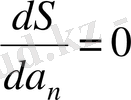 (4. 5)
(4. 5)
Егер (4. 1) эмпирикалық формулаға параметрлер сызықты болып енсе, онда (4. 3) тендеулер системасы сызықты тендеулер системасы болады. Сол сияқты сызықтық емес тендеулер системасын шешкеннен гөрі сызықтық теңдеулер системасын шешкен оңай, сондықтан мүмкіндігінше таңдап алынатын эмпирикалық формуланы, оған анықталған параметрлер сызықты кіретіндей етіп, тандап алу керек.
4. 3. Параметрлер арасындағы байланысты табу.
І. Сызықтық байланыс.
Түзу теңдеуі тәріздес теңдеу
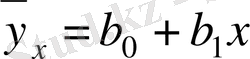 (1) факториалдық белгінің өсуімен, нәтижелік белгінің бір қалыпты өсу және кему кезінде қолданылады. Осындай байланыс сызықтық байланыс деп аталады. b
0
және b
1
параметрлерін табу үшін мына шартты пайдаланамыз:
(1) факториалдық белгінің өсуімен, нәтижелік белгінің бір қалыпты өсу және кему кезінде қолданылады. Осындай байланыс сызықтық байланыс деп аталады. b
0
және b
1
параметрлерін табу үшін мына шартты пайдаланамыз:
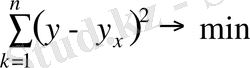 (4. 6)
(4. 6)
мұндағы у х орнына оның у х = b 0 +b 1 х мәнін қойып (4. 7) табамыз.
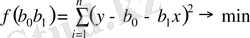 (4. 7)
(4. 7)
Бұдан екі параметр бойынша дербес туындылар тауып, оны 0-ге теңестіріп
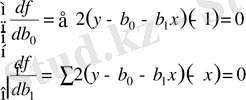 (4. 8)
(4. 8)
мына тендеулер системасын аламыз:
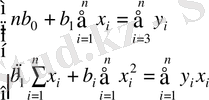
Бұл система параметрлерін табуға арналған ең кіші квадраттар тәсілінің
нормаль теңдеулер системасы немесе регрессия теңдеуі деп аталады. Нормаль тендеуді шешу жоғарғы алгебраның белгілі методикасы бойынша жүргізіледі, мұндағы n өлшеу саны,
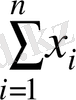 - факториалдық белгі мәнінің қосындысы,
- факториалдық белгі мәнінің қосындысы,
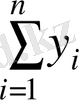 - нәтижелік фактордың мәнінің қосындысы,
- нәтижелік фактордың мәнінің қосындысы,
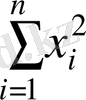 - факториалдық белгі мәнінің квадратының қосындысы
- факториалдық белгі мәнінің квадратының қосындысы
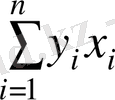 - факториалдық белгі мәнінің нәтижелік белгі мәніне көбейтіндісінің қосындысы.
- факториалдық белгі мәнінің нәтижелік белгі мәніне көбейтіндісінің қосындысы.
2, Параболалық байланыс
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz