Ондық көбейткіш құрылғыларын жобалау және басқару автоматын синтездеу


МАЗМҰНЫ
КІРІСПЕ7
1 ОНДЫҚ САНДАРДЫ КӨБЕЙТУДІҢ ЖЕДЕЛТЕТУ ТӘСІЛДЕРІ8
2 ОНДЫҚ КӨБЕЙТКІШТЕР ТҮРЛЕРІ14
2. 1 Толық разрядтыондық көбейткіш14
2. 2 Көбейтінді тетрадаларын тізбектеле өңдейтін ондық көбейткіш20
2. 3 Ондық көбейткіштердің сұлбасын салыстыру25
2. 4 Тиімді ондық көбейткіштің сұлбалары27
3 КӨБЕЙТІНДІ БАСҚАРУ АВТОМАТЫН СИНТЕЗДЕУ32
3. 1 Басқару автоматын синтездеу32
3. 2 Басқару автоматының электр принципиалдық сұлбасы35
3. 2. 1 Программаланатын логикалық матрицалар35
3. 2. 2 Басқару автоматының принциалдық электр сұлбасы42
3. 3 Тетрада шартбелгілегішін (ТШБ) синтездеу43
3. 4 Тетрада түрлендіргішін синтездеу47
3. 5 Тетрада түрлендіргішін синтездеу48
4 Еңбек қорғау бөлімі52
4. 1 Қауіпті және зиянды факторларды талдау52
4. 2 Қорғау шаралары55
4. 2. 1 Өндірістік санитария55
4. 3 Электрлік қауіпсіздігі59
4. 4 Өрт қауіпсіздігі59
5. ЭКОНОМИКАЛЫҚ БӨЛІМ67
5. 1 Жүйені енгізудің экономикалық тиімділігін есептеу68
5. 1. 1. Жүйені жасауға және енгізуге кететін шығындарды есептеу68
5. 1. 2. Техникалық құралдар кешенін сатып алуға кеткен шығындар69
5. 1. 3. Алгоритм дайындауға кеткен шығындарды есептеу69
5. 1. 4. Программаны енгізуге кететін шығындарды есептеу70
5. 1. 5. Программаны жазуға және түзетуге кететін шығындарды есептеу71
5. 2. Енгізуден бұрын жұмсалған шығындарды есептеу72
5. 3. Жүйені енгізгеннен кейінгі шығындарды есептеу73
5. 4. Шығындардың экономиясын есептеу74
ҚОРЫТЫНДЫ75
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ76
АНДАТПА
Диплом жобасында ондық көбейту құрылғыларының варианттары қаралып тиімді көбейткіш сұлбасы анықталады; оның көбейту микропрограммасы, басқару автоматын синтездеуі қаралады. Көбейту құрылғысының құрамына кіретін көбейту-қосындылау блогы, шартбелгілегіш құрылымы матрицалық үлкен шоғырланған сұлбаға лайықтала синтездеу жолы қаралады.
Annotation
In this diploma work considered varieties of device decimal multiplication, preferred schemes of economical multiplication, microprogramm of multiplication and control’s syntheses. Also considered synthesizing methods of parts multiplication device as multiplication-addition block and structure of conditions symbols agree with big concentrate schemes.
АННОТАЦИЯ
В дипломном проекте рассматриваются варианты устройства десятичного умножения, представлена схема экономичного умножения, микропрограмма умножения и синтез управления. Рассматриваются пути синтезирования составляющих умножающего устройства, т. е. блок умножения-сложения и структура условных знаков, в соответствии с большими концентративными схемами.
КІРІСПЕ
Қазіргі электронды есептеу машиналарының құрамына кіретін құрылғылардың бірі - ондық блоктар. Ондық блоктар ондық жүйеде көрсетілетін мәліметтер ағымын өндеп нәтижелерін ондық жүйеде сырт құрылғыларға беріп отырады. Ондық жүйеде өнделетін мәліметтерді екілік жүйеге немесе екілік жүйеден ондық жүйеге түрлендіруге керегі жоқ. Сондықтан мәліметтер ағымын ондық жүйеде өңдеу өте тиімді.
Ондық сандарды өңдегендегі ең көп уақыт керек ететін құрылғы ондық көбейткіштер болып табылады.
Көбейту құрылғысының жұмысын жеделтету арқылы машина өнімдігін арттыруға болады, өйткені ондық сандарды өндегенде көбейту амалы өте жиі орындалады.
Диплом жобасында ондық сандарды жеделдете көбейту тәсілдері қаралады. Құрамында есе сұлбалары бар ондық көбейткіштің жасалу жолдары қаралады. Тиімділік коэффициент арқылы олар бір-бірімен салыстырылып олардың тиімді варианты анықталады. Ондық көбейткіштің микропрограмма алынып оның негізінде басқару автоматтарының сұлбасы түзеледі.
Диплом жобасында есептеу сұлбасы синтезделеді. Ол екі бөліктерден тетрадасын көбейткішпен тетрадалы түрлендіргіштен тұрады. Кезекті жекеленген көбейтінді қосындысын алу үшін көбейткіштін симмериялық шартбелгісін алу керек. Сондықтан диплом жобасында тетрада шартбелгілегіш синтезделеді.
Еселеу сұлбасы мен тетрадасын шартбелгілегішті құру үшін элемент негізі ретінде программаланатын логикалық марица таңдап алынды. ПЛМ негізінде басқару автоматы еселеу сұлбасы, тетрадалық шартбелгілегіш синтезделеді.
1 ОНДЫҚ САНДАРДЫ КӨБЕЙТУДІҢ ЖЕДЕЛТЕТУ ТӘСІЛДЕРІ
Ондық сандарды көбейту ЭЕМ орындалатын операциялардың ішіндегі ең күрделі операциялардың қатарына жатады. Сондықтан көбейту амалын жеделдете ЭЕМ өнімділігін арттыруға болады. Төменгі 1-суретте ондық сандарды көбейтудің тәсілдері келтірілген [2] .
Логикалық тәсіл. Бұл тәсіл көбейткіш тетрада мәндерін азайтуға негізделген. Көбейткіш мәндері неғұрлым аз болса, онда дербес көбейтінді қосындылағышына (ДКҚ) көбейткіш аз қосылады. Ол үшін көбейткіш тетрада мәндерін көбейту үстінде түрлендіру керек. Ол үшін егер тетрада мәндері бестен көп болса, онда оны алға дейін толықтырып келесі тетрадаға “1”тасымасын береміз.
Мысал: А санын B=67981 санына көбейтейік. Егер көбейткіш тетрадасын түрлендірмеген, онда көбейту үйінде 31 қосындылау және 5 жылжыту операциялары орындалады. Түрлендіріп болған соң
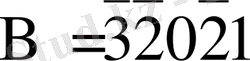 . Мұндай көбейткіште 8 қосындылау (азайту) амалдары және 5 жылжыту орындалады.
. Мұндай көбейткіште 8 қосындылау (азайту) амалдары және 5 жылжыту орындалады.
Көбейткіштің бір тетрадасы талдағанда орындалатын қосындылау (азайту) саны K * 1- кестеде келтірілген.
1- кесте - K * мәнін есептеу

+1М
+1М
+1М
+1М
+1М
+1М
+1М
+1М
+1М
+1М
+1М +1М
+1М
+1М
-1М
-1М
-1М
-1М
-1М
-1М
-1М
-1М
-1М
Аппаратты-логикалық тәсіл. Бұл тәсілде көбейту негізінде орындалатын қосындылау амалдар санын көбейту құрылғыларының құрамына аппараттар енгізу арқылы азайтылады.
Ол үшін көбейту амалын орындаудан бұрын көбейткішке есе мәндерін алдын ала есептеп (қосындағыш немесе арнайы сұлба арқылы) оларды регистрлерге сақтап қоямыз. Екінші тәсілде сұлбалар арқылы алып (қалыптастырып) оларды бірден осындалағыш кірістерін береміз.
Бірінші тәсілде есе мәндерін сақтау үшін регистрлер керек. Регистрлер саны алдын ала дайындалатын есе мәндер санымен анықталады.
Есе мәндері ішкі қосындалығыштар арқылы қалыптастырғанда есе мәндері тізбектеле бірінен соң бірі кезектеліп қалыптастырылады.
1-сурет - Ондық сандарды жеделдету тәсілдері
Есе мәндерін қатар дайындау үшін есе мәндерінің санымен анықталатын арнайы сұлбалар құру керек. Мұндай жекелеген сұлбалар арқылы мәндері арнайы регистрлерде сақталады.
Әр есе мәндері тетрадалары да параллель, тізбектеліп немесе параллель-тізбекті түрде қалыптастырылады.
Көбейту үстінде дербес көбейтінді операцияға тура немесе симметриялық шартбелгілерде қатысады.
Көбейтуді жеделдетудің аппараттың тәсілде көбейткіштен бірінші немесе барлық тетрадалары көбейту операцияларына қатынасады.
Көбейту амалын орындалу үстінде операцияларға қатынасатын операндтар тетрадалары тізбектелетін, параллель немесе тізбекті-параллель түрінде өңделеді. Ол көбейту құрылғысының құрамында болатын ондық қосындылағыштын разрядтылығына байланысты.
Тура және симметриялық шартбелгілеу көбейту үстінде орындалатын орта қосындылау саны - K * көбейтуде қолданылатын шартбелгілерге және есе жиынтық санымен (L) анықталады. 2-кестеде K * мәнінің есе жиынтық мәні мен оның санына байланысы болатын кейбір шамалары келтірілген.
2 - кесте - Әртүрлі жиындыққа сәйкес келетін K *
Есе мәндері
Тетрада
Мәндері
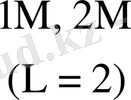
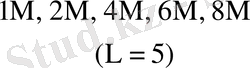
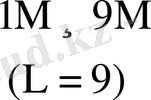
0
1
2
3
4
5
6
7
8
9
0
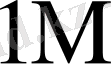



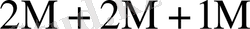
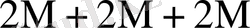
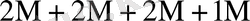
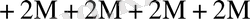
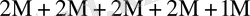
0
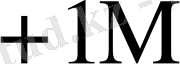
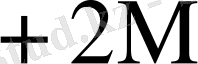
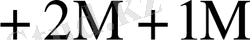
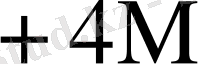
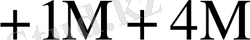
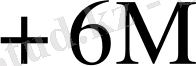
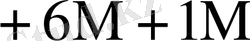
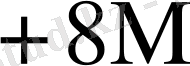
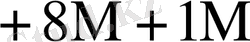
0
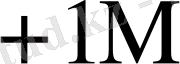
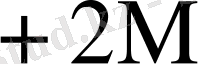
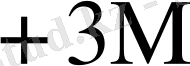
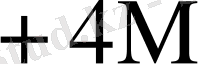

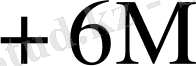

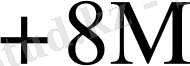
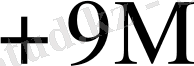
Бұл кестеден көрініп тұрғандай L өскен сайын K * бірге дейін азаяды.
 элементтерден тұратын көптеген есе жиынтықтарын көрсетуге болады. Олардың кейбіреулері төменде келтірілген:
элементтерден тұратын көптеген есе жиынтықтарын көрсетуге болады. Олардың кейбіреулері төменде келтірілген:
{1M, 2M}, {1M, 2M, 3M}, {1M, 2M, 3M, 4M};
{1M, 3M}, {1M, 2M, 4M}, {1M, 2M, 3M, 5M};
{1M, 4M}, {1M, 2M, 5M}, {1M, 2M, 3M, 6M}.
Бұл жерде 2M, 3M, . . . , 9M екі, үш . . . тоғыз еселенген көбейткіштер.
Мұндай жиынтық саны:
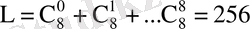 (1)
(1)
Әр жиынтыққа өзінің K
*
сәйкес келеді. 3-кестеде әртүрлі L-ге сәйкес келетін
 мәндері келтірілген.
мәндері келтірілген.
3-кесте - L мәндеріне сәйкес келетін
 мәндері
мәндері

4-кестеде симмериялық шартбелгі қолданғандағы әртүрлі L мәндеріне сәйкес келетін
 шамалары.
шамалары.
4-кесте - L мәндеріне сәйкес келетін

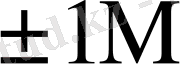
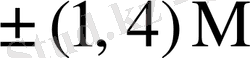
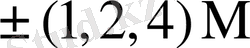
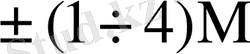
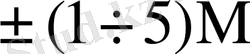

5-кесте - Есе мәндер жиынтығымен сәйкес келетін қосындылау санының орта мәндері.
Есе мәндері
Тетрада
мәндері


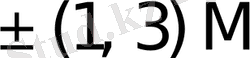
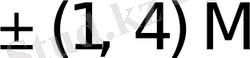
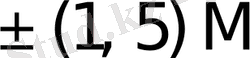
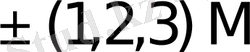
0
1
2
3
4
5
6
7
8
9
0


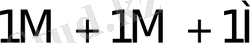
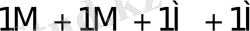
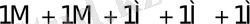
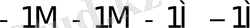
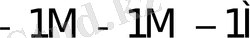
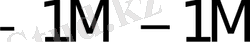

0



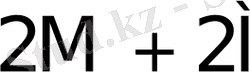




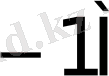
0

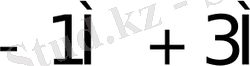


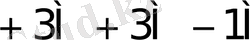

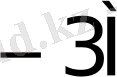
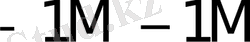

0





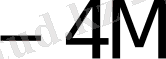


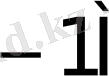
0


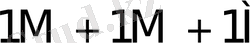



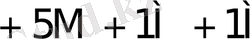
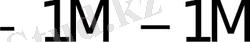

0



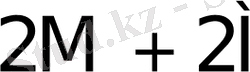


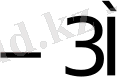

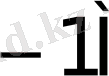
5-кесте жалғасы
Есе мәндері
Тетрада
мәндері
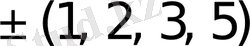
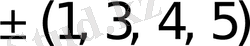
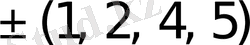
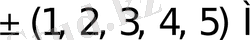
0
1
2
3
4
5
6
7
8
9
0




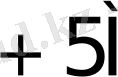
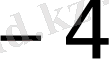



0



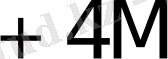
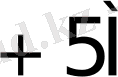
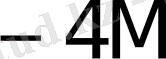
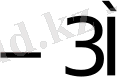

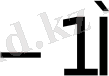
0



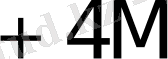
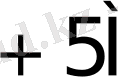
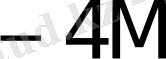

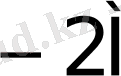

0



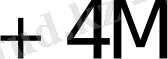
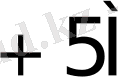
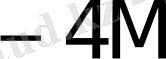
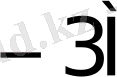
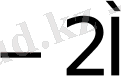

5-кесте жалғасы
Есе мәндері
Тетрада
мәндері
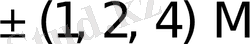
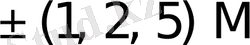
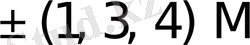
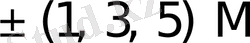
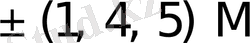
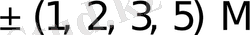
0
1
2
3
4
5
6
7
8
9
0


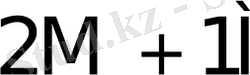
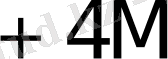

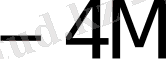



0


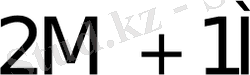
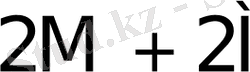




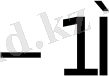
0



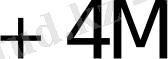

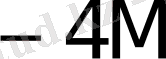
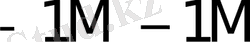

0






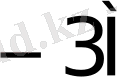
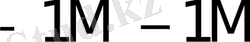
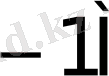
0



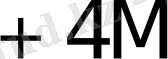

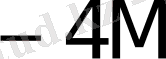

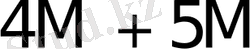

0



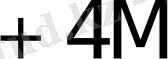

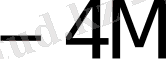

2 ОНДЫҚ КӨБЕЙТКІШТЕР ТҮРЛЕРІ
2. 1 Толық разрядты
 ондық көбейткіш
ондық көбейткіш
Мұндай қосындылағыш құрылымдар сұлбасы 2, 3-суреттерде келтірілген. 1-суретте
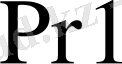 және
және
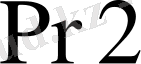 регистрлерінде көбейткіш көбейту амалының орындалуының алдында кіріс шипасынан алынып жазылып қойылады.
регистрлерінде көбейткіш көбейту амалының орындалуының алдында кіріс шипасынан алынып жазылып қойылады.
Жекелеген көбейтінді қосындылары және екі санын көбейтіндісі
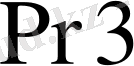 регистрінде сақталады. Регистр
регистрінде сақталады. Регистр
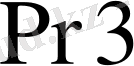 ең кіші тетрадасы
ең кіші тетрадасы
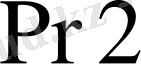 регистрінің жоғарғы тетрадасымен байланысты.
регистрінің жоғарғы тетрадасымен байланысты.
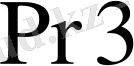 бір тетрадаға оңға қарай жылжығанда одан шыққан тетреданы
бір тетрадаға оңға қарай жылжығанда одан шыққан тетреданы
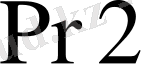 регистрдің жоғарғы тетрадасына жазамыз. Мұндай байланыс операция аяқталып болған соң
регистрдің жоғарғы тетрадасына жазамыз. Мұндай байланыс операция аяқталып болған соң
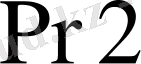 -де көбейтіндінің екінші бөлігі
-де көбейтіндінің екінші бөлігі
 деп
деп
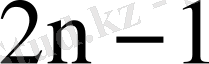 разрядтарын алуға мүмкіңдік береді.
разрядтарын алуға мүмкіңдік береді.
Еселеу сұлбасы (Есл) толық разрядты
 . Есл кірістеріне бір кірістеріне
. Есл кірістеріне бір кірістеріне
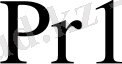 регистрінен берілсе екінші кірістеріне
регистрінен берілсе екінші кірістеріне
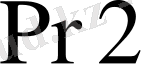 кіші тетрадаларынан беріледі де оның шығысынан екінші кірісіне берілетін тетрада мәніне байланысты
кіші тетрадаларынан беріледі де оның шығысынан екінші кірісіне берілетін тетрада мәніне байланысты
 тетрадасы көбейткіш мәні алынады да олар ондық қосындылағыштар бірінші кірісіне беріледі. Ондық қосындалыштың екінші кірісіне
тетрадасы көбейткіш мәні алынады да олар ондық қосындылағыштар бірінші кірісіне беріледі. Ондық қосындалыштың екінші кірісіне
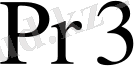 регистрінің шығысынан бұл такттың алдында қалыптасқан жекелеген көбейткіш қосындысы берілген.
регистрінің шығысынан бұл такттың алдында қалыптасқан жекелеген көбейткіш қосындысы берілген.
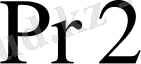 және
және
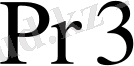 регистрлерінде жылжыту тізбектері бар. Олар регистрде жазылған.
регистрлерінде жылжыту тізбектері бар. Олар регистрде жазылған.
Шартбелгі төрт разрядтарға (бір тетрадаға) жылжытып отырады.
Көбейтінді белгісі екі модулімен қосу арқылы белгі триггерінде Т Бл аламыз. Ол үшін белгілер шартбелгіін белгі дешифраторларының кірістеріне беріп олардың унитар мәндерін аламыз. Көбейткіштің тетрада санын тетрада санағышы (ТСАН) бақылайды.
Көбейткіш тетрадалардың барлығына көбейтіп шыққанда
 және
және
 болады. Алынған нәтиже шығыс шинасына беріледі.
болады. Алынған нәтиже шығыс шинасына беріледі.
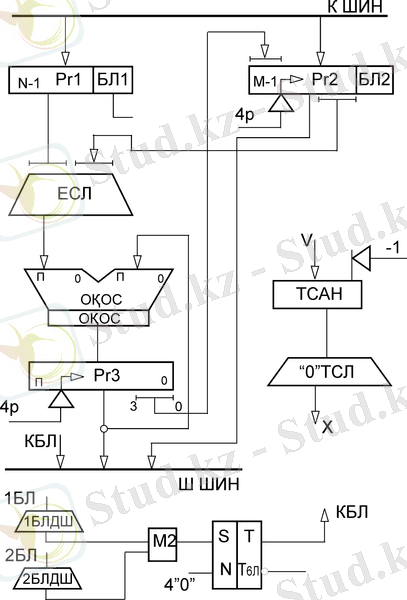
2 - сурет -
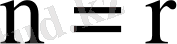 болғандағы ондық көбейту сұлбасы (тура шартбелгі)
болғандағы ондық көбейту сұлбасы (тура шартбелгі)
Көбейту амалының орындалуы 3-суретте көрсетілген.
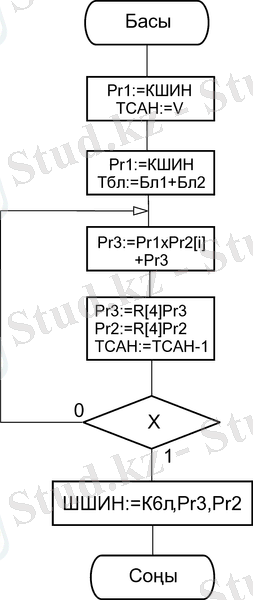
3-сурет - Толық разрядты көбейткіштің тура шартбелгіде көбейту алгоритмі
Толық разрядты көбейткіштің екінші варианты. Көбейткіштің еселеу
сұлбасы бұдан бұрынғы қаралған еселеу сұлбасынан өзгеше. Мұнда бірінші кірісіне көбейткіштің тетрадалары берілсе екінші кірістеріне үш разрядты шартбелгі беріледі. Көбейткіш тетрадасының мәні бестен артық екендігін көрсетіп разряд
 түрлендіргіш кірісіне беріледі. Егер
түрлендіргіш кірісіне беріледі. Егер
 болса, онда есе тетрада мәні кері шартбелгіде алынады, ал
болса, онда есе тетрада мәні кері шартбелгіде алынады, ал
 болса, онда көбейтінді тетрадасы ондық қосындылағыш кірістен тура шартбелгіде беріледі.
болса, онда көбейтінді тетрадасы ондық қосындылағыш кірістен тура шартбелгіде беріледі.
Көбейткіштің талданатын тетрадасы тетрада шартбелгілеріне (ТШБ) арқылы түрлендіріліп симметриялық шартбелгі алынады. Оны төменде келтірілген кестемен көрсетуге болады.
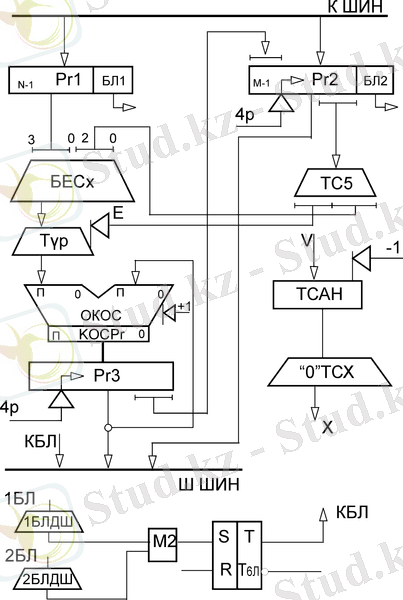
4-сурет - n=r болғандағы ондық көбейткіш сұлбасы (симметриялық шартбелгі) .
6-кесте - Тетрада шартбелгілегісінің жұмыс кестесі

0001
0010
0011
0100
0101
0110
0111
1000
1001
0
0
0
0
0
0
0
0
0
0
0001
0010
0011
0100
0101
0100
0011
0010
0001
0
0
0
0
0
0
1
1
1
1
001
0010
0011
0100
0101
0110
0111
1000
1001
1
1
1
1
1
1
1
1
1
1
0001
0010
0011
0100
0101
0100
0011
0010
0001
0
0
0
0
0
1
1
1
1
1
Сонымен еселеу сұлбасының екінші кірістеріне
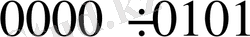 шартбелгілері ғана беріледі. Ал талданған тетрада мәні алтыдан артық болса
шартбелгілері ғана беріледі. Ал талданған тетрада мәні алтыдан артық болса
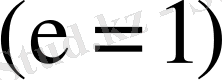 , онда еселеу сұлбасының шығысынан алынған тетрада мәндері кері шартбелгіде қалыптасады.
, онда еселеу сұлбасының шығысынан алынған тетрада мәндері кері шартбелгіде қалыптасады.
Көбейткіштің қалған түйіндері жоғарыда қаралған көбейту құрылғысының жұмыстарына ұқсас.
5-суретте қаралып отырған көбейткіштегі көбейту алгоритмі.
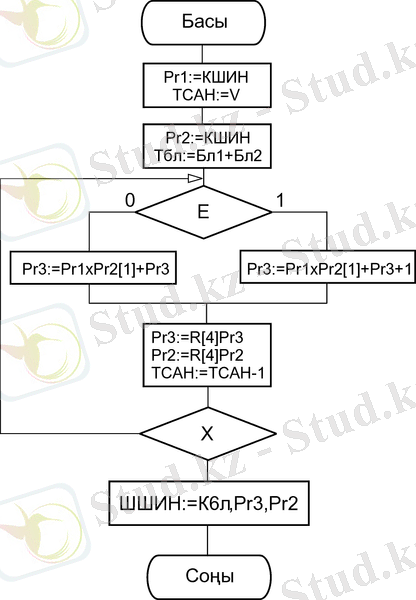
5-сурет - Толық разрядты көбейткіштің симметриялық шартбелгіде көбейту алгоритмі
2. 2 Көбейтінді тетрадаларын тізбектеле өңдейтін ондық көбейткіш

Қаралып отырған көбейткіш сұлбасы 6-суретте келтірілген. Сұлбада мультиплексор (МХ1) арқылы көбейткіш байттары байт елеу сұлбасының (БЕСЛ) бірінші кірістеріне беріледі. Оның екінші кірістеріне
 мән алатын.
мән алатын.
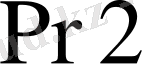 регистрінің кіші тетрадасынан беріледі.
регистрінің кіші тетрадасынан беріледі.
Ондық байт қосындылағыштың (ОБҚОС) екінші кірістеріне мультиплексор МХ2 арқылы
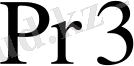 регистрінен байттар беріледі. Олар кезек-кезек қосындыланып алынған әтижелер демультиплексор арқылы
регистрінен байттар беріледі. Олар кезек-кезек қосындыланып алынған әтижелер демультиплексор арқылы
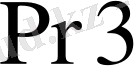 регистріне кезек-кезек жазылады.
регистріне кезек-кезек жазылады.
Байт санағышы (БСАН) арқылы байт сандары бақыланып отырылады. Ал тетрада санағышы (ТСАН) арқылы көбейту амалы орындалуының аяқталуы бақылап отырады.
Көбейту алгоритмі 7-суретте келтірілген. Операндтарды
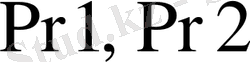 регистрлеріне жазған соң көбейткіштің кіші разряды көбейткіштің тетрадаларына кезекпен көбейтіліп алынған байт байт қосындалығышына беріледі. Ол
регистрлеріне жазған соң көбейткіштің кіші разряды көбейткіштің тетрадаларына кезекпен көбейтіліп алынған байт байт қосындалығышына беріледі. Ол
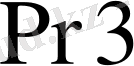 регистріне алынатын байттармен қосындыланып кезекті жекеленген көбейтінді қосындысын алып
регистріне алынатын байттармен қосындыланып кезекті жекеленген көбейтінді қосындысын алып
 регистрін демультиплексор арқылы жазады.
регистрін демультиплексор арқылы жазады.
 болғанда алынған нәтиже төрт разрядтарға оңға қарай жылжытылып, егер
болғанда алынған нәтиже төрт разрядтарға оңға қарай жылжытылып, егер
 болса көбейту циклы қайта басталады.
болса көбейту циклы қайта басталады.
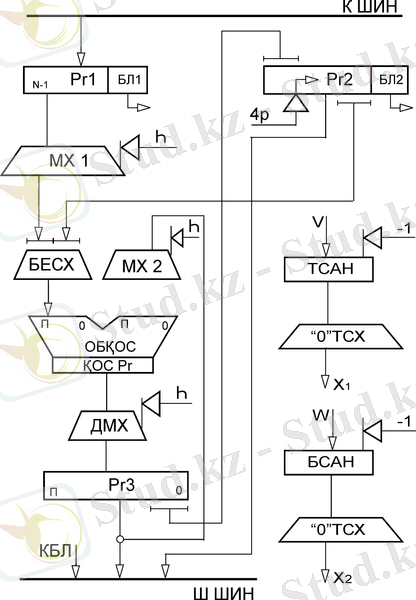
6-сурет - n>r болғандағы ондық көбейткіш сұлбасы (тура шартбелгі)
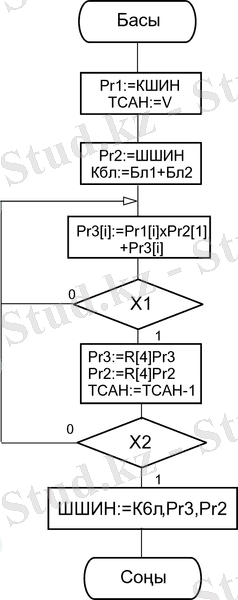
7-сурет - Тура шартбелгіде көбейту алгоритмі
Көбейтінді тетрадаларын тізбектеп өңдейтін көбейткіш сұлбасының екінші түрі 8-суретте көрсетілген
Бұл көбейткіштің бұрынғы көбейткіштерден айырмашылығы жекеленген көбейтінді қосындалығыш арқылы алынады. Сондықтан мультиплексор МХ1 және мультиплексор МХ2 арқылы операндтар
 регистрінен және
регистрінен және
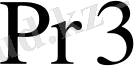 регистріне тізбектеліп алынып оар еселеу сұлбасы мен ондық ондық қосындылағыш кірістеріне тізбектеле беріледі. Көбейту сұлбасының құралып тетрадаға санғышы мен байт санағышы (егер операндтар байтпен өңделсе) енгізілген көбейту алгоритмі 9-суретте келтірілген.
регистріне тізбектеліп алынып оар еселеу сұлбасы мен ондық ондық қосындылағыш кірістеріне тізбектеле беріледі. Көбейту сұлбасының құралып тетрадаға санғышы мен байт санағышы (егер операндтар байтпен өңделсе) енгізілген көбейту алгоритмі 9-суретте келтірілген.
Операндтарда
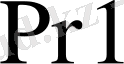 және
және
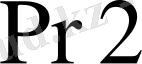 регистрлеріне алып болған соң
регистрлеріне алып болған соң
 мәніне байланысты жекеленген көбейтінді қосындысы ондық қосындылағыш арқылы тізбектеліп не тура, не симметриялық шартбелгідее қалыптастырылады. Байт саны (егер көбейткішті байтпен бөліп өңделген) байт санағышы арқылы
мәніне байланысты жекеленген көбейтінді қосындысы ондық қосындылағыш арқылы тізбектеліп не тура, не симметриялық шартбелгідее қалыптастырылады. Байт саны (егер көбейткішті байтпен бөліп өңделген) байт санағышы арқылы
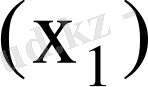 бақыланса, көбейткіш тетрадаы тетрада санағышы арқылы бақыланады.
бақыланса, көбейткіш тетрадаы тетрада санағышы арқылы бақыланады.
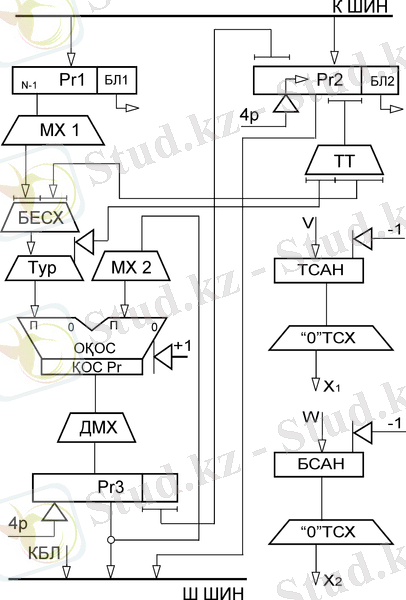
8-сурет - n>r болғандағы ондық көбейткіш сұлбасы (симметриялық шартбелгі)
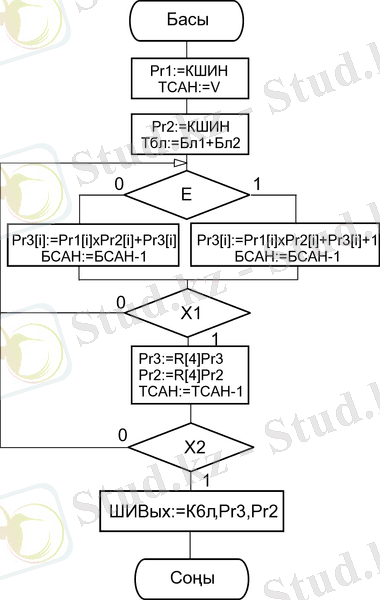
9-сурет - Симметриялық шартбелгіде тізбектей көбейту алгоритмі.
2. 3 Ондық көбейткіштердің сұлбасын салыстыру
Жоғарыда қаралған ондық көбейткіштердің ең тиімді түрін анықтау үшін олардың тиімді коэффициенттерін анықтаймыз:
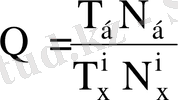 (2)
(2)
мұнда
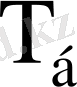 - құрамында еселеу сұлбасы ток көбейту құрылғысындағы көбейту уақыты, мәні;
- құрамында еселеу сұлбасы ток көбейту құрылғысындағы көбейту уақыты, мәні;
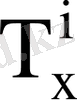 - құрамында еселеу сұлбасы бар
- құрамында еселеу сұлбасы бар
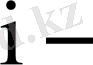 көбейткіштің көбейту уақыты;
көбейткіштің көбейту уақыты;
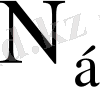 - құрамында еселеу сұлбасы жоқ көбейткіштің аппараттық
- құрамында еселеу сұлбасы жоқ көбейткіштің аппараттық
шығыны (көбейткішті құратын логикалық сұлбалардың кіріс саны) ;
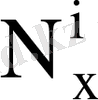 - құрамында еселеу сұлбасы бар
- құрамында еселеу сұлбасы бар
 көбейткіштің аппараттық
көбейткіштің аппараттық
шығыны;
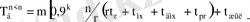
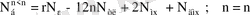 болғанда
болғанда
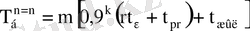
 . (3)
. (3)
Құрамында еселеу сұлбасы бар көбейту құрылғылары үшін
 (тура шартбелгі) :
(тура шартбелгі) :
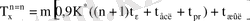 ;
;
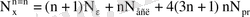 . (4)
. (4)
 (тура шартбелгі)
(тура шартбелгі)
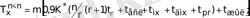
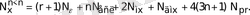 (5)
(5)
 (симметриялық шартбелгі)
(симметриялық шартбелгі)
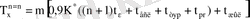
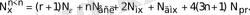 (6)
(6)
 (симметриялық шартбелгі)
(симметриялық шартбелгі)
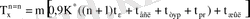
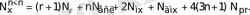 (7)
(7)
 (симметриялық шартбелгі)
(симметриялық шартбелгі)

 (8)
(8)
Жоғарыдағы формулаларда:
- ондық қосындылағыштар (бір тетрадалы) құратын логикалық
сұлбалар кіріс саны;
- регистрдегі жылжыту уақыты;
-
 бір тетраданы талдағанда керек орындалатын қосындылау
бір тетраданы талдағанда керек орындалатын қосындылау
санының орта мөлшері;
-
 көбейткіш тетрада саны;
көбейткіш тетрада саны;
-
 көбейгіш тетрада саны;
көбейгіш тетрада саны;
-
 еселеу сұлбасы мен түрлендіргіш, ондық қосындылағыш тетрада
еселеу сұлбасы мен түрлендіргіш, ондық қосындылағыш тетрада
саны;
-
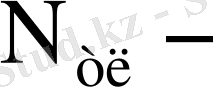 триггер құратын қосындалағыш және еселеу сұлбаларындағы
триггер құратын қосындалағыш және еселеу сұлбаларындағы
кідіріс уақыты;
-
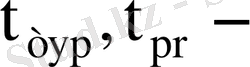 бір разрядты түрлендіргіш және регистр кідіріс уақыт мөлшерлері;
бір разрядты түрлендіргіш және регистр кідіріс уақыт мөлшерлері;
-
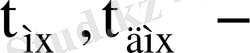 мультиплексор мен дешифраторлардағы кідіріс уақыты;
мультиплексор мен дешифраторлардағы кідіріс уақыты;
-
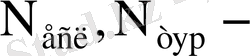 еселеу сұлбасы мен түрлендіргіштер құратын логикалық сұлбалардың кіріс сандары;
еселеу сұлбасы мен түрлендіргіштер құратын логикалық сұлбалардың кіріс сандары;
-
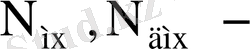 мультиплексор мен дешифраторлар құратын сұлбалардың кіріс сандары.
мультиплексор мен дешифраторлар құратын сұлбалардың кіріс сандары.
10-суретте тура шартбелгіде жұмыс жасайтын ондық көбейткіштер үшін
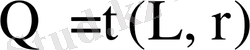 графигі келтірілген.
графигі келтірілген.
11-суретте симметриялық шартбелгіде жұмыс жасайтын көбейткіштер үшін
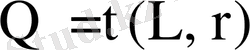 графигі келтірілген.
графигі келтірілген.
Бұл графиктерден көрініп тұрғандай ең тиімді көбейткіш параметрі
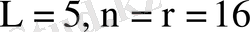 және жекеленген көбейтінді қосындысын алу үшін симметриялық шартбелгі қолдану керек.
және жекеленген көбейтінді қосындысын алу үшін симметриялық шартбелгі қолдану керек.
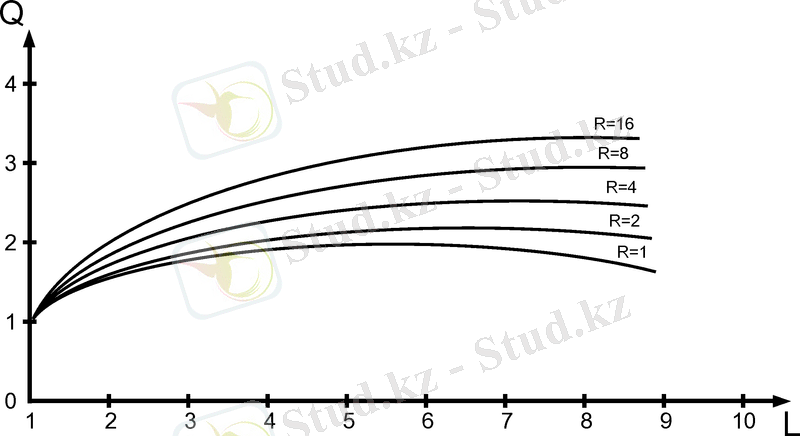
10-сурет - Q = f (L, R) тура шартбелгі графигі
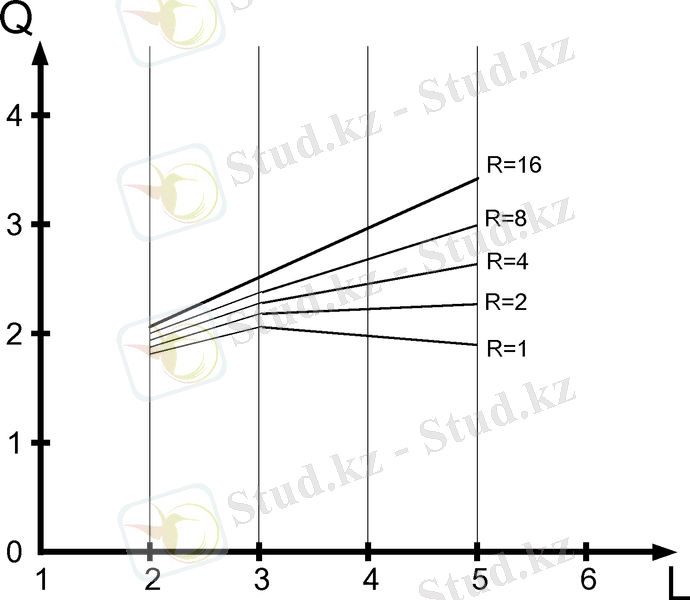
11-сурет - Q = f (L, R) симметриялық шартбелгі графигі
2. 4 Тиімді ондық көбейткіштің сұлбалары
Жоғарыда
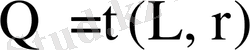 тәуелділігінен ең тиімді көбейту құрылғысын симметриялық шартбелгіде жұмыс жасайтын толық разрядты көбейткіш болатындығын анықтадық.
тәуелділігінен ең тиімді көбейту құрылғысын симметриялық шартбелгіде жұмыс жасайтын толық разрядты көбейткіш болатындығын анықтадық.
12-суретте толық разрядты ондық көбейткіштің бірінші варианты көрсетілген. Бұл сұлбада көбейткіш тетрадасы тетрада шартбелгісі арқылы белгіленіп, ол еселеу сұлбасында мәні түрлендіріліп кірісіне беріледі. Еселеу сұлбасы арқылы көбейткіштің тетрадалары
 мәніне көбейтіледі. Егер
мәніне көбейтіледі. Егер
 мәні бірге тең болса, онда ол көбейтіндінің кіші тетрада мәнін кері шартбелгіге түрлендіріледі. Қосындылау кезінде ондық қосындылағыштың кіші разрядына бір қосылады. Яғни көбейткіш симметриялық шартбелгіде жұмыс жасайды.
мәні бірге тең болса, онда ол көбейтіндінің кіші тетрада мәнін кері шартбелгіге түрлендіріледі. Қосындылау кезінде ондық қосындылағыштың кіші разрядына бір қосылады. Яғни көбейткіш симметриялық шартбелгіде жұмыс жасайды.
13-суретте көбейткіштің екінші варианты берілген. Мұнда екі кезекті тетрадаға көбейткенде еселеу схемасы кірісіне көбейткіштің үш разрядтарынан басқа тасымал разрядтары да беріледі. Тасымал разрпяд мәніне және көбейтінді тетрада мәніне байланысты еселеу.
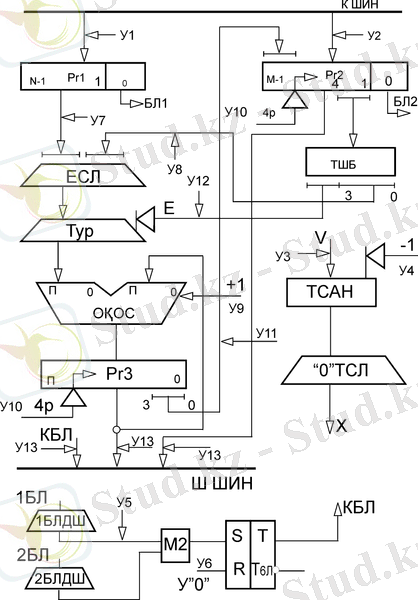
12-сурет - Толық разрядты (n=r) симметриялық шартбелгіде жұмыс жасайтын ондық көбейткіш (1-вариант)
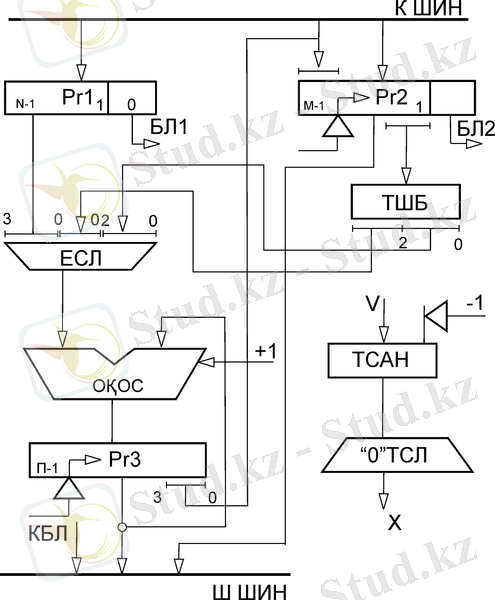
13-сурет - Толық разрядты симметриялық шартбелгіде жұмыс жасайтын ондық көбейткіш (2- вариант)
Сұлбаның шығысынан көбейтіндінің кіші тетрадасы ондық қосындылағыштың кірістеріне тура немесе кері шартбелгіде беріледі.
14-суретте көбейткіштің микропрограммасы көрсетілген.
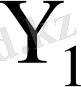 - микрокомандасынан кіріс шинадан
- микрокомандасынан кіріс шинадан
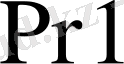 регистріне көбейгіш жазылады.
регистріне көбейгіш жазылады.
 - микрокомандасынан
- микрокомандасынан
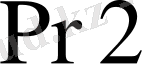 регистрінде кіріс шинадан (КШИН) көбейгіш енгізіледі және тетрада санағышын
регистрінде кіріс шинадан (КШИН) көбейгіш енгізіледі және тетрада санағышын
 санының (
санының (
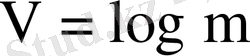 ) шартбелгісі жазылады. Көбейтінді белгісі анықталып, ол белгі триггеріне жазылады.
) шартбелгісі жазылады. Көбейтінді белгісі анықталып, ол белгі триггеріне жазылады.
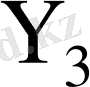 және
және
 микрокомандасы арқылы
микрокомандасы арқылы
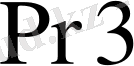 регистрінде жекеленген көбейтінді қосындысы алынады.
регистрінде жекеленген көбейтінді қосындысы алынады.
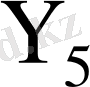 микрокомандасы арқылы
микрокомандасы арқылы
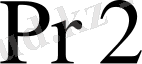 және
және
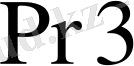 регистрлері оңға қарай төрт разрядтарға жылжытылады, тетрада санағышынан бірді алып тастайды. Алынған нәтиже
регистрлері оңға қарай төрт разрядтарға жылжытылады, тетрада санағышынан бірді алып тастайды. Алынған нәтиже
 болғанда шығыс шинасына шығарылады.
болғанда шығыс шинасына шығарылады.
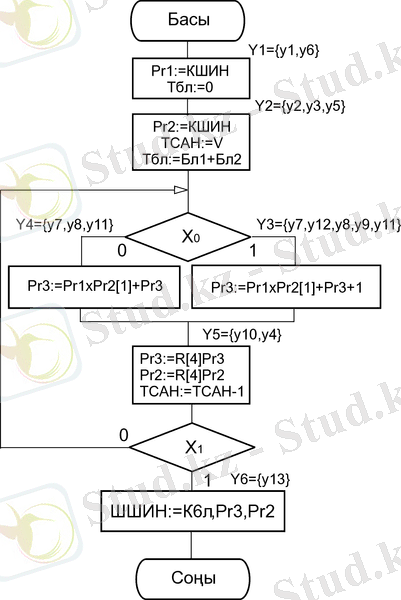
14-сурет - Көбейту микропрограммасы
Көбейту құрылғысында төмендегідей микрооперациялар орындалады:
y 1 : Pr1 : = КШИН:
y 2 : Pr2 : = КШИН:
y 3 : TCAH : = V:.
y 4 : TCAH : = TCAH-1:
y
5
: T
Бл
: = Бл1
 Бл1:
Бл1:
y 6 : T Бл : = 0:
y 7 : ЕСЛ : = Pr1:
y 8 : ЕБЛ : = ТШБ:
y 9 : ОКОС : = ОКОС +1:
y 10 : Pr3 : = R[n] Pr3 и Pr2 : = R[n] Pr2:
y 11 : ОКОС : = Pr3:
y
12
: ТYP : =
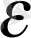 :
:
y 13 : КБЛ, Pr2, Pr3.
3 КӨБЕЙТІНДІ БАСҚАРУ АВТОМАТЫН СИНТЕЗДЕУ
Көбейткіштің басқару автоматы екі блоктан тұрады. Біріншісі - басқару автоматы. Екіншісі - тетрада шартбелгілегіші. Басқару автоматы операциялық автоматтан шарт сигналымен (х
0
және х
1
) автоматтың ішкі күйіне байланысты басқару сигналдарын
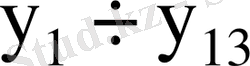 шығарады. Ал тетрада шартбелгілегіші талданатын көбейткіш тетрадасының мәніне байланысты тетрада көбейткіштің кірістеріне симметриялық шартбелгі береді.
шығарады. Ал тетрада шартбелгілегіші талданатын көбейткіш тетрадасының мәніне байланысты тетрада көбейткіштің кірістеріне симметриялық шартбелгі береді.
Басқару автоматын синтездеу мынандай кезеңдерден тұрады:
- көбейту микропрограммасын пайдалана автоматтың граф сұлбасын алу;
- граф - сұлбасын белгілеу;
- автоматтың күйін ықшамдау;
- автоматтың құрылымдық сұлбасын құру;
- қозу функциясын және шығыс функцияларын алып оларды ықшамдау;
- автоматтың функционалдық сұлбасын алу;
- автоматтың элемент негізін таңдау;
- автоматтың электр принциалдық сұлбасын құру.
3. 1 Басқару автоматын синтездеу
Автоматтың граф-сұлбасы көбейткіш микропрограммасы негізінде жасалынады.
15- суретте автоматтың белгіленген граф-сұлбасы келтірілген.
Суреттен көрініп тұрғандай автомат бес күйде бола алады -
 . Автомат жадын D триггерде құрамыз.
. Автомат жадын D триггерде құрамыз.
Автомат күйлерін төмендегідей шартбелгілейміз.
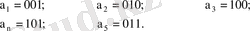
Автомат күйін ықшамдау үшін Вейч-Карно кестесін пайдаланамыз
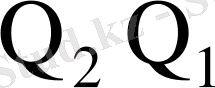
00 01 11 10

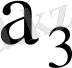
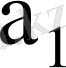
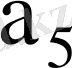

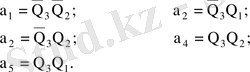
Автоматтың құрылымдық кестесі - кестеде келтірілген.
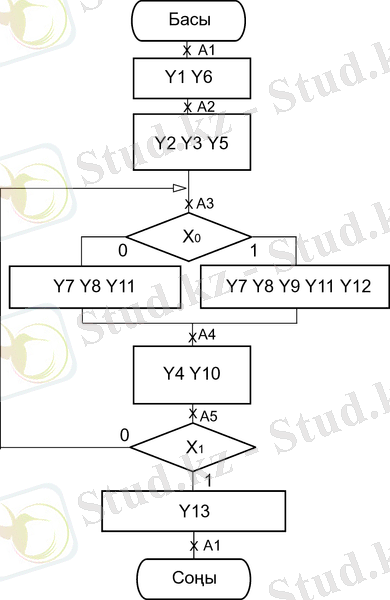
15-сурет - Автоматтың граф-сұлбасы
7-кесте - Автоматтың құрылымдық кестесі
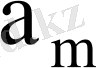
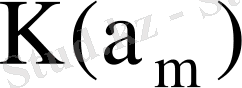
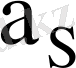
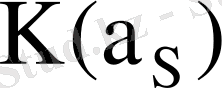
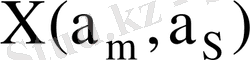
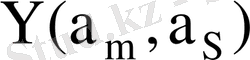
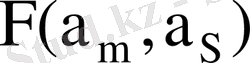
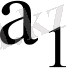

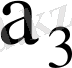
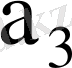

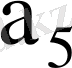
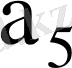
001
010
100
100
101
011
011

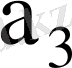


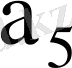
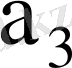
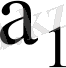
010
100
101
101
011
100
001
-
-
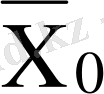
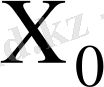
-
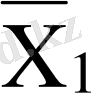
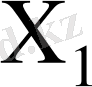
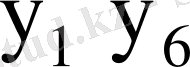
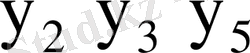
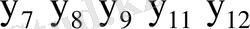
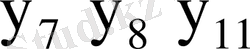
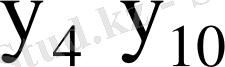
-
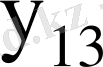


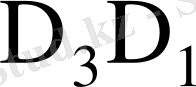
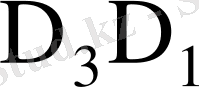
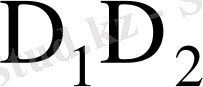

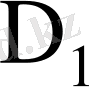
Қосу функциясы:
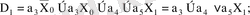
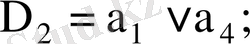
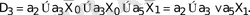
Шығыс функциясы:
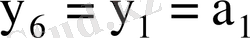 :
:
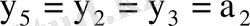 :
:
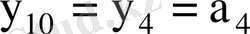 :
:
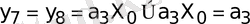 :
:
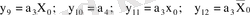 :
:
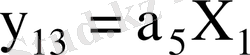 .
.
3. 2 Басқару автоматының электр принципиалдық сұлбасы
3. 2. 1 Программаланатын логикалық матрицалар
Программаланатын логикалық матрицалар (ПЛМ) жартылай өткізгіштер технологиясы атты жасалынған функционалдық блок болып табылады. Олар цифрлық жүйелердегі логикалық сұлбаларды алу үшін қолданылады [3] . Ішкі құрылымдарын ұйымдастыруына байланысты ПЛМ екі түрге бөлінеді: комбинациялық логикалық және құралымында жады бар ПЛМ деп ПМЛ-нің бірінші түрінің ішінде екі деңгейлі түрі кеңінен қолданып отыр. Әдетте олар екі
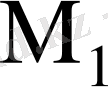 және
және
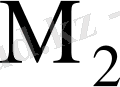 матрицаларынан тұрады.
матрицаларынан тұрады.
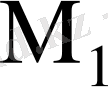 матрицасында
матрицасында
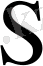 кірістер және
кірістер және
 шығыстар болады.
шығыстар болады.
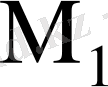 де
де
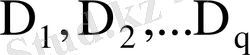
 элементтер конъюнкцияларын алуға мүмкіндік береді. Конъюнкциялар кірістеріне
элементтер конъюнкцияларын алуға мүмкіндік береді. Конъюнкциялар кірістеріне
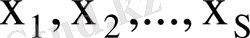 кіріс айнымалылары беріледі.
кіріс айнымалылары беріледі.
Матрица
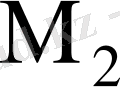
 кірістері және
кірістері және
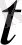 шығыстары бар. Мұнда
шығыстары бар. Мұнда
 шығыстары берілген
шығыстары берілген
 айнымалылар арқылы
айнымалылар арқылы
 элементер дизъюнкциялар алынады.
элементер дизъюнкциялар алынады.
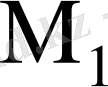 матрицасының шығыстары
матрицасының шығыстары
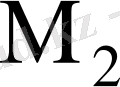 матрицасының кірістерімен байланыста болады және
матрицасының кірістерімен байланыста болады және
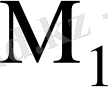 шығыстары ПЛМ
шығыстары ПЛМ
 аралық шиналарын құрады.
аралық шиналарын құрады.
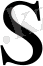 кірістері,
кірістері,
 шығыстары және
шығыстары және
 аралық шиналары бар ПЛМ(
аралық шиналары бар ПЛМ(
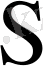 ,
,
 ,
,
 ) деп атаймыз.
) деп атаймыз.
Бір ПЛМ(s, t, q) -те
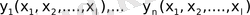 Equation. 3 функция жүйесін іске қосуға болады. Бұл жерде
Equation. 3 функция жүйесін іске қосуға болады. Бұл жерде
 . В - элементар конъюнкция саны.
. В - элементар конъюнкция саны.
16-суретте ПЛМ(s, t, q) сұлбасының құрылымы және оның шартты белгісі көрсетілген.
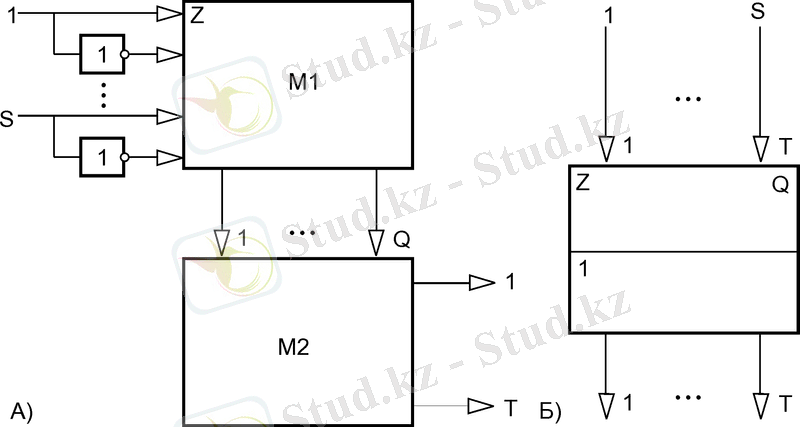
16-сурет - ПЛМ (S, t, q) құрылымдық сұлбасы
ПЛМ(s, t, q) түрлерінің бірі: ПЛМ(z, q) . Мұнда ПЛМ екі параметрлері көрсетіледі: кіріс және шығыс сандары z=s+t шина саны. Егер z саны көрсетілсе s және t мәндері ПЛМ(z, q) арқылы оларды бағдарлау арқылы анықталады. Мысалы, ПЛМ (6, 10) оны программалау арқылы мынадай варианттарын алуға болады. ПЛМ (3, 3, 10), ПЛМ (5, 1, 10) т. б.
8-кестеде ПЛМ-нің кейбір параметрлері берілген (1-10 қатарлар)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ППЛМ SN74 330 331
ППЛМ IM 5200
MПЛМ MMI 5775A
MПЛМ MMI 6870/71
MПМ MMI 6775/75A
MПЛМ DM 8575 175A
MПЛМ DM 7576
ППЛМ 93458/59
ППЛМ 825100/101
ППЛМ 556 PTI
ППЛМД
 PB 450
PB 450
ППЛМД
 PB 450 A-1
PB 450 A-1
ППЛМ 82 S104/105
ППМB 82 S102/103
ППB 29 693
12
14
14
14
14
14
14
16
16
16
24
24
16
16
10
6
8
8
8
8
8
8
8
8
8
16
16
8
9
4
50
48
96
48
56
96
96
48
48
48
72
72
48
-
3
30
104
80
-
80
-
-
25
50
50
100
70
90
35
-
-
-
-
-
-
-
-
-
-
-
16
16
6
-
-
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz