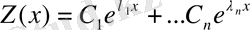Дифференциалдық теңдеулер жүйесін шешу: Коши есебін Эйлер әдісімен және MATLAB сандық әдістері


ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛІГІ
Қ. И. Сатпаев атындағы қазақ ұлттық
техникалық университеті
техникалық кибернетика кафедрасы
КУРСТЫҚ ЖОБАҒА
түсініктеме парағы
тақырыбы: Дифференциалдық теңдеулер жүйесі
Жетекші
ғылыми дәрежесі мен атағы
Мұртазина Ә. У.
5. 05. 2004 жыл
Нормабақылаушы
Аты-жөні:
5. 05. 2004 жыл
Студент Әмірбеков Ж. А.
Мамандығы 370140
Тобы ИВТ-02-2қ
Алматы 2004
МАЗМҰНЫ
КІРІСПЕ2
1 Есептің қойылымы4
2. НЕГІЗГІ БӨЛІМ6
2. 1 Сандық әдістің түрлері6
2. 2 Коши есебін шығару10
3 MatLab функциялары13
4 MatLab көмегімен есептеулерді орындау15
1. Реттерін төмендетуге болатын теңдеулер15
2. Тұрақты коэффициенттері арқылы берілген сызықты біртекті теңдеулер21
Теориялық анықтама21
ҚОРЫТЫНДЫ25
ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ26
КІРІСПЕ
Көптеген процестердің математикалық түрі, ізделінетін белгісіз шама цифр емес, ал белгілі бір аргументке тәуелді функция ретінде берілетін теңдеумен өрнектеледі. Сонымен қатар, бұл функция өз туындысы және аргументімен байланысты болады. Бұндай теңдеулер дифференциалдық теңдеулер деп аталады.
Дифференциалдық теңдеулер математикалық анализ жүргізуде үлкен роль атқарады.
Жұмыстың мақсаты: дифференциалдық теңдеулер жүесін тереңірек зертттеу, MatLab пакетінің дифференциалдық теңдеулер жүйесін шешуге арналған функцияларымен танысу, сандық әдістерді оқып-білу.
Қойылған проблеманың актуальдығы: қазіргі кезде техниканың дамуына байланысты әр түрлі химиялық, физикалық заттардың құрамын, массасын, көлемін, ұзындығын, т. б. - параметрлерін зерттеу қажеттігі туып отыр. Одан басқа бұл параметрлердің уақытқа және де т. б. шамаларға тәуелділігін де білу керек. Мұның бәрін тек дифференциалдық теңдеулер жүйесі көмегімен ғана жүзеге асыруға болады.
Қазіргі уақытта дифференциалдық теңдеулер техника ғылымдарынң барлық дерлік салаларында кең қолданысқа ие болып отыр.
1 Есептің қойылымы
Көптеген процесстердің математикалық түрі, ізделінетін белгісіз шама цифр емес, ал белгілі бір аргументке тәуелді функция ретінде берілетін теңдеумен өрнектеледі. Сонымен қатар, бұл функция өз туындысы және аргументімен байланысты болады. Бұндай теңдеулер дифференциалдық теңдеулер деп аталады.
Мысалы, бір радиоактивті элементтің массасы m болсын. Бұл массаның уақытқа байланысты өзгеруін зерттеу керек. M массаның уақытқа тәуелділігін келесі түрде жазуға болады: m=m(t), мұндағы t - белгілі бір моменттен бастап саналған уақыт. Бұл уақытты шартты түрде нөлге тең деп аламыз (t=0) .
M(t) массасының Δt уақыт арасында өзгеруі m(t) Δt туындысына пропорционал№ Егер β пропорционалдық көэффиценттін енгізсек, келісі теңдеуді алуға болады:
M(t + Δt) - m(t) = -βm(t) Δt (1. 1)
Мұндағы теңдеудің оң жағындаға минус таңбасы m(t) массасының уақытқа байланысты азаятынын көрсетеді. (1. 1) теңдеуінің екі жағын да Δt бөлу арқылы:
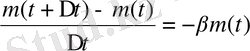
Δt🡪 0 ұмтылған кезде келесідей теңдеуге келеміз:
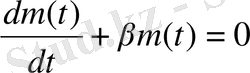 (1. 2)
(1. 2)
Бұл теңдік t уақытының әрбір мәніне m функциясының және оның мәнін байланыстырады, яғни дифференциалды болып табылады.
2. Қайсібір қоршаған ортада бөлінумен көбиетін біржасушала организмдер бар болсын дейік. Уақыт бірлігінде әрбір N жасуша β N бөлінеді. β - көбею коэффиценті деп аталады. t уақыт аралығындағы жалпы организм санын βN(t) Δt арқылы белгілейік. Нәтижесінде келесі теңдеуді аламыз:
N(t+ Δt) - N(t) = βN (t) Δt
Теңдіктің екі жағын да Δt бөліп, шектік өткізу Δt🡪 0 жасасақ, дифференциалдық теңдеу аламыз:
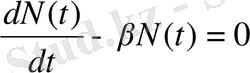 (1. 3)
(1. 3)
3. Кез келген массасы М-ге тең болатын дене бар түзуді қарастырайық. Бұл түзудің бойынан кез келген а нүктесін белгілейміз, а нүктесі мен М дененің арасындағы ара қашықтықты S әріпімен белгілейміз. Қозғалыста тұрған М денесіне, уақытқа тәуелді F күші әсер етсін, сол кезде S шамасы уақыт функциясы болады. S және F тәуелділігін анықтайық: F=F(t), S=S(t) . Мұндағы S(t) - дененің а нүктесінен F(t) күш әсерінен t уақыт арасында жүретін жолы делік. Егер S(t) дененің t уақыт ішінде жүрген жолы болса, онда оның t-дан t + Δt уақыт арасында жүрген жалдамдығы V келесі формуламен есептелінеді:
V=
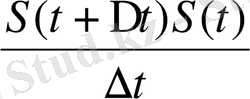
Δt нөлге ұмтылдырып:
V(t) =
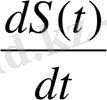 Equation. 3
Equation. 3
Аламыз. Яғни, дененің нүктедегі жылдамдығы функияның уақыт бойынша туындысына тең.
Есебімнің қойылымы: Эйлер әдісімен Коши есебін шығару
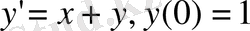
2. НЕГІЗГІ БӨЛІМ
2. 1 Сандық әдістің түрлері
- Айнымалыларды ажырылатын теңдеулерді шешу.
Бірінші тектес дифференциалдық теңдеу келесі түрде берілген кезде ғана оны айнымалылары ажырылатын теңдеу деп атайды:
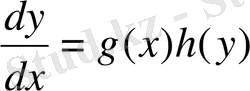 (2. 1)
(2. 1)
Айнымалылары ажырылатын теңдеудің жалпы шешімін табу керек. (2. 1) теңдеуін келесі түрде жазамыз:
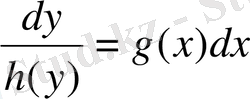
Соңғы теңдіктің екі жағын да интегралдап, түрлендірсек:
(2. 2)
(2. 2) теңдеуінің туындылары жоқ, бірақ бірнеше қасиеттері бар.
интегралы есептеліп f(y) -ке тең болды делік. Онда былай жазуға болады: f(y) -
. Егер бұл жерден у-ті нақты түрде табу мүмкін болса, онда (2. 1) теңдеуінің жалпы шешімін аламыз. Бірақ та, у-ті айқын түрде бейнелеу өте сирек кездеседі. Теңдеуді шешу барысында у =y(x, C) өрнегімен қатар:
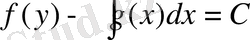
өрнегі де үлкен роль атқарады. Бұл (2. 1) теңдеуінің жалпы интегралы деп аталады.
Айнымалылары ажырылатын теңдеулерді шешудің тағы да бір жолын қарастырайық. Кез келген
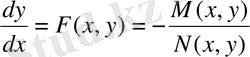
бірінші ретті теңдеуді келесі түрде жазуға болады:
M(x, y) dx +N(x, y) dy=0 (2. 3)
Жазылудың мұндай түрі ыңғайлырақ болып келеді: белгісіз функцияны таңдаудың қажеті жоқ. Белгісіз функция ретінде y=y(x) немесе x=x(y) теңдіктерін алуға болады. Егер M(x, y) және N(x, y) әрқайсысы тек бір айнымалыға tәуелді екі функциялардың туындылары болып табылса, (2. 3) теңдеуі айнымалылары ажырылатын теңдеу болып табылады.
M 1 (x) M 2 (y) dx + N 1 (x) N 2 (y) dy=0 (2. 4)
Шынымен де, теңдеудің екі жағын да N 1 (x) M 2 (y) , бөлсек:
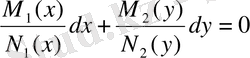
және (2. 4) теңдеуінің жалпы интегралын аламыз:
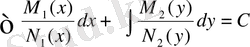
Сонымен, айнымалылары ажырылатын теңдеулердің жалпы интегралын табу, екі анықталмағын интегралдың шешімін табуға әкеп соқтырады. Осындай, бір есептің шешімін екінші есепке түрлендіру редукция деп аталады.
- Біртеті емес тұрақты коэффиценті бар сызықтық дифференциал теңдеулерді шешу.
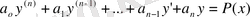
 (2. 5)
(2. 5)
түрдегі тұрақты коэффиценті бар біртектіемес сызықтық дифференциал теңдеуді шешудің бірнеше жолдарын қарастырайық. Мұнда: а
о
, а
1
, . . . , а
n
- кез келген сандар.
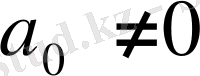 Equation. 3, P(x) - кез келген функция. (2. 5) теңдеуімен қатар оған сәйкес біртекті теңдеуді қарастырайық:
Equation. 3, P(x) - кез келген функция. (2. 5) теңдеуімен қатар оған сәйкес біртекті теңдеуді қарастырайық:
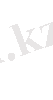 (2. 6)
(2. 6)
Т е о р е м а 1. y 1 (x) (2. 5) теңдеуінің шешімі, ал y 2 (x) (2. 6) теңдеуінің шешімі болсын. Онда y 1 (x) + y 2 (x) (2. 5) теңдігінің шешімі болады.
1 теореманы біртекті емес теңдеудің жалпы шешімін құру үшін қолдануға болады, егер оның кез келген жергілікті тундсы белгілі болса. Шынында да, y 1 (x) - (2. 5) - тің жергілікті шешімі болсын. Оның сәйкес біртекті теңдеуінің шешімі белгілі дей отырып, оның түрі келесідей болады:
1 теорема бойынша:
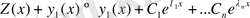 (2. 7)
(2. 7)
теңдеуі біртекті емес теңдеудің шешімі болып табылады. Бірақ,
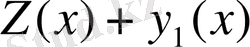 С
1
, С
2
, . . . , С
п
тұрақтыларына тәуелді, олай болса анықтама бойынша, (2. 5) теңдеуінің жалпы шешімі болып табылады. Бұл қорытындының арқасында келесі теореманы айтуға болады.
С
1
, С
2
, . . . , С
п
тұрақтыларына тәуелді, олай болса анықтама бойынша, (2. 5) теңдеуінің жалпы шешімі болып табылады. Бұл қорытындының арқасында келесі теореманы айтуға болады.
Т е о р е м а 2. (2. 5) біртекті емес теңдеуінің жалпы шешімі белгілі бір біртеіті емес теңдеудің жергілікті шешемі мен біртекті теңдеудің жалпы шешімінің қосындысы болып табылады.
Бұл теорема біртекті емес теңдеулерді шешудің әмбебап түрі - біртекті теңдеуді жалпы шешімі табылады да, оған біртекті емес теңдеудің кез келген жергілікті шешімі қосылады.
М ы с а л ы
1.
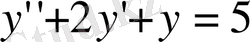
теңдеуінің жалпы шешімін табу керек.
у=5 тұрақтысы бастапқы біртекті емес теңдеудің жергілікті шешімі болып табылады. Шынында да:
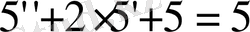
Енді біртекті теңдеудің жалпы шешімін табайық. Оның түрі келесідей:
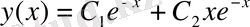
2 теорема бойынша бастапқы теңдеудің жалпы шешімі келесі түрге ие:
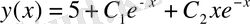
Табылған шешімнің дұрыстығын дифференциалдау арқылы табуға болады.
(2. 5) біртекті емес теңдеудің 2 жергілікті шешімі бар болсын. Оларды y 1 (x) және y 2 (x) арқылы белгілейік. Егер у(х) сәйкес біртекті теңдеуінің жалпы шешімін табатын болсақ, онда y 1 (x) +у(х) және y 2 (x) +у(х) бастапқы біртекті есем теңдеудің жалпы шешімі болады да бір ортақ шешімнің әртүрлі формасы болып табылады.
Т е о р е м а 3. Біртекті емес екі теңдеулердің жергілікті шешімдерінің айырымы болып, сәйкес біртекті теңдеудің жергілікті шешімі табылады.
Жалпы жағдайда біртекті емес теңдеудің шешімін табу қиын, бірақ, егер Р(х) күрделі функция болмаса, мүмкін. Жиі-жиі кездесетін мысалдарды талдайық.
а) Р(х) - белгілі бір келесі көпмүше P(x) =b 0 x m +b 1 x m-1 +…+b m-1 x+b m . Жергілікті шешімін m дәрежедегі көпмүше түрінде табамыз. Коэффиценттерін теңдіктің екі жағындағы тең дәрежелерді теңестіру арқылы табамыз. Мысалы, келесі теңдеудің жергілікті шешімін табатан болсақ:
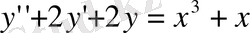
шешімін:
y(x) =ax 3 +bx 2 +cx+d
түрінде табамыз. Мұндағы a, b, c, d - әзірше белгісіз шамалар
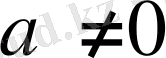 . Теңдеуге у(х) қойып, келесі теңдікті аламыз:
. Теңдеуге у(х) қойып, келесі теңдікті аламыз:
(6ax+2b) +2(3ax 2 +2bx+c) +2(ax 3 +bx 2 +cx+d) =x 3 +x.
Бұдан шығатыны:
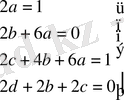
Ізделініп отырған қорытқы шешімнің түрі:
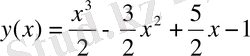
б) P(x) =(b 0 x m +b 1 x m-1 +…+b m ) e ax алайық. Шешімін m дәрежесін e ax дәрежеге шығарылатын туынды арқылы іздейміз. Коэффиценттерін жоғарыдағы мысалдағыдай табамыз. Мысалы, келесі теңдеудің жергілікті шешімін табу керек:
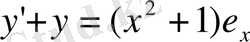
шешімін
y(x) =(ax 2 +bx+c) e x
түрде іздейміз.
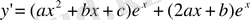 ескере отырып, коэффицентті берілген теңдеуден анықтаймыз:
ескере отырып, коэффицентті берілген теңдеуден анықтаймыз:
(ax 2 +bx+c) e x +(2ax+b) e x +(ax 2 +bx+c) e x =(x 2 +1) e x
e x -ке қысқартқаннан кейін және х-тің бірдей дәрежелерін теңестіргеннен кейін:
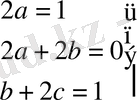
аламыз. Ізделінетін жергілікті шешім келесі түрде болады:
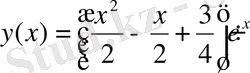
2. 2 Коши есебін шығару
Дифференциалды теңдеулердің тек кейбіреулерінің шешімін белгілі элементер функция арқылы табуға болады. Ол қарапайым мынандай теңдеу болса да:
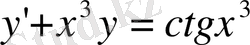
оның функциясы арқылы табылатын шешімі жоқ. Сондықтан да дифференциалды теңдеулерді шешуде тура шешім емес, жобалап тапқан шешімдер зор роль арқарады. Жобалап шығарудың екі жолы бар - аналитикалық-жобалама және сандық әдіс.
Дифференциалдық теңдеуді а н а л и т и к а л ы қ - ж о б а л а м а арқылы шығару деп соңғысы аналитикалық өрнек түрінде берілетін жобалама шешімді табуды айтады. Бұл әдістің артықшылығы оның шешімі кез келген аналитикалық тәсілдермен зерттеулуі мүмкін. Шешімнің, ешқандай қосымша мәліметті қолданбай, туындылары мен интегралдарын есептеуге, максимум, минимум немес иілу нүктелерін табуға болады. Бірақта, аналитикалық-жобалама шешімді табу кей кезде қиын болады.
С а н д ы қ ә д і с т е р г е дифференциалдық теңдеудің шешімдерін кесте түрде алғанды жатқызады. Бұл кезде шешімнің аналитикалық түрі белгісіз. Сондықтан дифференциалық теңдеуді сандық әдіспен шығару қосымша қиындықтармен шектелген. Мысалы, мұндай шешімнің туандасын табу үшін сандық дифференциалдыу әдісі пайдаланылады; интегралын табу үшін квадратура формулалары қолданылады. Ал табылған шешімді экстримумге зерттеу мүлдем мүмкін емес.
Соған қарамастан да, сандық әдіс аналитикалық-жобалама әдісіне қарағанда біршама артықшылықтарға ие. Ең бастысы, олар есептеуіш қондырғыларды пайдаланыла алады.
Ең алғашында, бірінші ретті дифференциал теңдеулер үшін Коши есебін шығарудың жобалама жолы Эйлер болып есептелді.
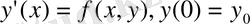 берілсін. х
0
нүктесіндегі y=f(x) функциясынан туынды алу анықтамасы бойынша: y=f(x) функциясының x=х
0
нүктесіндегі туындысы деп:
берілсін. х
0
нүктесіндегі y=f(x) функциясынан туынды алу анықтамасы бойынша: y=f(x) функциясының x=х
0
нүктесіндегі туындысы деп:
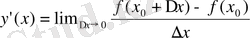
Бұдан мынандай қорытындыға келуге болады:
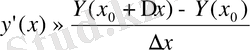 (2. 8)
(2. 8)
ақырлы Δх кезінде. Аланған (2. 8) теңдігі Эйлер жолының негізінде жатыр.
х осіне, х=0 ден бастап, бір бірінен τ ара қашықтықта болатын нүктелерді орналастырамыз. х 1 =τ, х 2 =2τ, . . . , х n =nτ, … деп белгілейік. Осындай нүктелердің жиынтығы бізге торды береді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz