Кездейсоқ сандар генераторы

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 27 бет
Таңдаулыға:

1 Кездейсоқ сандарды генерациялау

1. 1 Ақиқат кездейсоқ сандар және олрды қолданудың мәселелері

Кілтті генерациялау үшін бізге кездейсоқ сандарды генерациялауыш (random number generator - RNG) керек. Жақсы кездейсоқтықтың генерациясы - расында да көптеген криптографиялық операциялардың ең қажетті және сонымен қатар аса ауыр бөліктерінің бірі.

Біз кездейсоқтықтың өзімен расында нені білдіретінін онша толық қарастырмаймыз. Осы терминнің көптеген әдемі математикалық анықтамалары бар, бірақ олардың бәрі бұл жобада қарастыру үшін өте ауыр. Ал формальсыз емес жағынан егер де қолданушы кездейсоқтықпен күресу үшін белсенді әрекеттер қолданатын болса да, кездейсоқтықты қаскүнем үшін болжамсыз мәліметтер мәндері ретінде анықтауға болады.

Көптеген криптографиялық функцияларға жақсы кездейсоқ сандардың генераторлары керек. Біз А және Б қолданушыларға белгілі кілт бар деп жорамалдадық. Бұл кілт бір жерде шығарылу керек. Кілттерді таңдау үшін кілттерді басқару жүйесі кездейсоқ сандардың генераторын қолданады. Егер генератор онша мықты болмаса, нашар кілт алынады. Тап осы жағдай Netscape шолушысының ерте нұсқаларының бірінде болды.

Кездейсоқтықтың өлшемі энтропия (entropy) деп аталады. Мен бұл жерде осы сұрақтың математикалық бөліктерін келтіріп жатпаймын, жай ғана энтропияның не екенін түсіндіру үшін барлығын жасауға тырысамын. Егер бізде мүлде кездейсоқ түрмен таңдалатын 32-биттік сөз болса, онда оның 32 бит энтропиясы болады. Егер де 32-биттік сөз әрқайсысының шығу ықтималдығы 25%-ға тең тек 4 мән қабылдай алатын болса, онда бұл сөз тек 2 бит энтропияға ие болады. Энтропия мәндегі биттің санын емес, осы мәнде сіздің қаншаға сенімсіз екендігіңізді көрсетеді. Көбірек суреттеу үшін энтропияны қысудың тамаша алгоритімін қолдану кезінде мәнді беру үшін керек биттің орташа саны ретінде қарастыруға болады. Назар аударыңыздар, мәннің энтропиясы осы мән туралы қанша білетініңізге байланысты. 32-биттік кездейсоқ сөздің 32 бит энтропиясы бар. Енді осы сөздің мәні туралы келесілер нақты белгілі деп қарастырайық: сөздің 18 биті 0-ге тең, ал 16 бит - 1-ге тең. Бұндай талаптарға жуықтап 2 ^{28, 8} мән қанағаттандырады, осыдан шығатыны, сөздің энтропиясы тек 28, 8 битті құрайды. Басқа сөзбен айтқанда, неғұрлым мән туралы көбірек білсек, соғұрлым оның энтропиясы аз болады.

Кездейсоқ үлестірілуі бір қалыпты болмайтын мәндер үшін энтропияны есептеп шығару біраз қиындау. Х айнымалысының энтропиясын анықтаудың ең кең тараған түрі келесі түрде құралады:

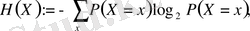
мұндағы Р(Х=х) - Х айнымалысының х мәнін қабылдау ықтималдығы. Біз бұл формуланы қолданбаймыз, сондықтан оны есте сақтаудың керегі жоқ. Энтропия туралы айтқанда математиктер тап осы анықтамаға жүгінеді. Математикада энтропияның тағы да бірнеше анықтамалары бар; ғалымдардың анықтаманың не ананы, не мынаны таңдауы ғалымның нақты немен айналысатынына байланысты. Және біздің энтропияны физикадағы нақты термодинамикаға жататын энтропиямен шатастырмаңдар.

Тамаша әлемде «ақиқат кездейсоқ» сандарды қолданған дұрыс болар еді. Өкінішке орай, біздің әлем тамаша емес және онда шындығында кездейсоқ мәліметтер табу өте қиын.

Кәдімгі компьютерлерде энтропияның бірнеше көздері бар. Осындай көздердің мысалы ретінде көбінесе перненің дәл басылу уақыты мен тышқанның орын ауыстыруының дәл уақыты келтіріледі. Кезінде кейбір ғалымдар қатты дискіге жету уақытының оның корпусының ішіндегі турбуленттікпен шақырылған тербелістерінің кездейсоқтығына зертеулер жүргізген. Осы барлық энтропиялардың көздері күмән туғызады, өйткені кейбір нақты жағдайларда қаскүнем кездейсоқтықтың көзінің үстінен есептеулер жүргізуі немесе осы көзге әсер етуі мүмкін.

Көптеген өңдеушілер әр түрлі көздерден алынуы мүмкін энтропияның санына оптимистік көзбен қарайды. Біз перненің бір басылуы кезінде уақытқа байланысты 1-2 байт кездейсоқ мәліметтерді шығарған бағдарламалық қамтамасыздандырылуды көрдік. Өкінішке орай, біз бұл оптимистікпен келіспейміз. Перненің кәсіби машинстпен басылу уақытын бірнеше миллисекундқа дейінгі дәлдікпен болжауға болады. Ал перненің басылу уақытын өлшеуге болатын пернетақтаны сканерлеу жиілігін дәлдік шектейді. Басылып жатқан мәліметтерді де, тіпті қолданушы жай ғана бірінші кездескен пернелерді басатын болса, кездейсоқтық деп атауға болмайды. Одан әрі жаманы, әрқашан қаскүнемде «кездейсоқ» оқиғалар туралы қосымша ақпараттың бар болуының қаупі болады. Пернені басқан кезде шығатын дыбыстарды әрбір перненің басылу уақытын анықтауға мүмкіндік беретіндіктен микрофонға жазып алуға болады. Энтропияның ана не мына мәліметтерде бар санын бағалағанда өте сақ болыңыздар. Анығында, біз өте ақылды және белсенді қаскүнеммен кездесіп отырмыз.

Өзін кездейсоқ түрде ұстайтын көптеген физикалық процестер бар. Мысалы, кванттық физиканың заңдары бойынша кейбір бөлшектердің жүрісі толық кездейсоқтық болып табылады. Осы кездейсоқ жүрісті өзіміздің жүйеде қолдану үшін есептеп шығарсақ жақсы болар еді. Техникалық жағынан бұл әрине мүмкін. Өкінішке орай, қаскүнемдерде бұл жерде де өздерінің жолдары болады. Біріншіден, ол болжанатындай етіп кванттық бөлшектердің жүрісіне ықпал тигізуі мүмкін. Екіншіден, ол жай ғана біздің өлшеулерді ұрлап кете алады. Егер қаскүнем өлшеулерді алатын болса, онда мәліметтер бәрібір кездейсоқ болып қалады, бірақ, оның ойынша, ешқандай да энтропияға ие болмайды (егер қаскүнем дәл мәнді білетін болса, онда ол мән оған энтропия болып саналмайды) . Мүмкін, қаскүнем біздің құралдардың көрсетулерін өзгертетін күшті радиосәуле шығара алады. Тіпті біз кванттық физиканың заңдарын қолданатын бірнеше шабуылдарды суреттей аламыз. Мысалы, біз өлшейін деп жатқан кездейсоқтықты бұзу үшін Эйнштейн-Подольский-Розен породоксы қолданылуы мүмкін. Осыған ұқсас пікірлер энтропияның басқа да көздеріне, мысалы, резистордың жылу кедергілері немесе жартылай өткізгіштіктік стабилитрондағы туннел әсері қолданылады.

Кейбір қазіргі заманғы компьютерлерде енгізілген ақиқат кездейсоқ сандардың генераторлары бар. Бұл, сөзсіз оларға жеке генераторларды қолдану алдында түбегейлі артықшылықтар береді, өйткені, кейбір шабуылдардың кейбір түрлерінің орындалуына айтарлықтай кедергі жасайды. Әйтсе де мұндай кездейсоқ сандар генераторы әлі де операциялық жүйеге қол жетерліктей болады, сондықтан қосымшалар қауіпсіз мәліметтер алу үшін оған толық сенуі керек.

Ақиқат кездейсоқ сандарды алудың қиындығынан басқа, оларды практикада қолданудың басқа да бірнеше мәселелері бар. Біріншіден, олар әрқашан қол жететіндей болмайды. Егер кездейсоқ сандар пернені басу уақытының негізінде шығарылатын болса, қолданушы кенеттен жазуды тоқтататын болса, сіз ешқандай мәлімет алмайсыз. Егер сіздің қосымшаңыз пернетақтасы жоқ компьютерге орнатылған Web-сервер болатын болса, бұл нағыз мәселе болуы мүмкін. Осыған ұқсас тағы бір мәселе ақиқат кездейсоқ сандардың көлемі әрқашан шектеулілігімен байланысты. Егер сізге үлкен көлемді кездейсоқ сандар керек болса, көптеген қосымшаларға мүлде қолайсыз болатын олар шығарылғанша тосуға тура келеді.

Екінші мәселе кездейсоқ сандардың физикалық генераторлары секілді ақиқат кездейсоқ сандардың көздері сынып қалуы немес бет қайтару мүмкіндігінде. Кей кездерде генератордың іс-әрекеті болжамды болуы мүмкін. Өйткені ақиқат кездейсоқ сандардың генераторы күрделірек, олар компьютердің классикалық компоненттеріне қарағанда тез істен шығуы мүмкін. Егер сіздің жүйеңіз ақиқат кездейсоқ сандардан тікелей тәуелді болса, ол бет қайтарған уақытта сіздің жолыңызда үлкен кедергілер болады.

Және үшінші мәселе - ол нақты физикалық оқиғалардан алына алатын энтропиияның бағалану қиындығы. Бірақ егер кездейсоқ сандардың генераторы ретінде белгіленген, арнайы осыған жасалған құрал қолданылмайтын болса, алынып жатқан энтропияның санын анықтау өте қиын болады.

1. 2 Жалғанкездейсоқ сандар және оларды қолданудың мәселелері

Ақиқат кездейсоқ сандардың орнына жақсы құрал ретінде жалғанкездейсоқ сандар қолданылады. Шындығында, жалғанкездейсоқ сандар жалпы кездейсоқ болып саналмайды. Олар детерминантты алгоритмнің көмегімен кейбір бастапқы сандардың (seed) негізінде табылады. Бастапқы санды біле отырып келесі барлық жалғанкездейсоқ сандарды болжауға болады. Классикалық жалғанкездейсоқ сандардың генераторлары (pseudorandom number generator - PRNG) ақылды қаскүнемнен ешқалай сақтандырылмаған. Олар шабуылдарды тоқтату үшін емес, статистикалық бұрмалауларды жою үшін жасалынған. Дональд Кнуттың (Donald Knuth) The Art of Computer Programming кітабының екінші томында кездейсоқ сандардың генераторларының толық суреттемесі жазылған, бірақ олардың барлығы статистикалық кездейсоқтыққа қатысты зерттелген. Біз қарсыластың кездейсоқ сандардың шығаруына қолданылатын алгоритмді білетіндігінен бастауымыз керек. Алгоритммен шығарылған бірнеше жалғанкездейсоқ сандарды біле отырып қаскүнем кейбір алдыңғы (немесе өткендегі) кездейсоқ сандардың биттерін болжай ала ма? Көптеген классикалық жалғанкездейсоқ сандардың генераторлары үшін жауап ақиқат болуы мүмкін. Жалғанкездейсоқ сандардың криптографиялық генераторларына бұл мүмкін емес жағдай.

Криптографиялық жүйенің контексінде жалғанкездейсоқ сандардың генераторларына одан да гөрі қатаң сұранымдар келтіріледі. Егер қаскүнем генератормен құрылған кездейсоқ сандардың толық қатарын білетін болса да, ол онда қалған кездейсоқ сандар туралы қандай да бір ақпаратты болжауға мүмкіндігі болмауға тиіс. Біз бұндай жалғанкездейсоқ сандардың генераторларын криптографикалық мықты деп атаймыз. Жалғанкездейсоқ сандардың классикалық генераторлары керегі жоқ болғандықтан, әрі қарай біз тек криптографикалық мықты генераторлар туралы айтатын боламыз.

Сіздің бағдарламалық кітапханаңызда бар жай кездейсоқ функцияларды ұмытыңыздар. Олардың біреуі де криптографиялық жүйелерде қолдануға жарамайды. Көптеген бағдарламалық кітапханалар жеңіл статистикалық тесттерден де өте алмайтын жалғанкездейсоқ сандардың генераторларымен беріледі. Ешқашан, егер құжаттамасында олар криптографиялық мықты деп жазылмаған болса, кітапханалық генераторларды қолданбаңыздар.

1. 3 Ақиқат кездейсоқ сандар және жалғанкездейсоқ сандардың генераторлары.

Ақиқат кездейсоқ сандарды біз тек жалғанкездейсоқ сандардың генераторларына кіріс беретін бастапқы сандарды табу үшін ғана қолданамыз. Бізде бастапқы сан табылғаннан кейін генератор өмірге кездейсоқ (толығырақ жалғанкездейсоқ) сандардың кез-келген санын шығара алады. Керек болған жағдайда біз ақиқат кездейсоқ сандарды кездейсоқ сандардың генераторының бастапқы санына қоса аламыз. Бұл, егер қаскүнем қандай да бір түрмен бастапқы санды біліп алған болса да, ақырғының шығыс мәліметтері ешқашан толық болжамды болмайтындығына кепілдік бере алады.

Ақиқат кездейсоқ сандар жалғанкездейсоқ сандардан гөрі жақсырақ деген теориялық ой бар. Кейбір криптографиялық хаттамалар үшін ақиқат кездейсоқ сандарды қолдану кезінде шабуылдың белгілі кейбір түрлері мүмкін болмайтындығын дәлелдеуге болады. Мұндай хаттама сөзсіз қорғалған (unconditionally secure) деп аталады. Егер де жалғанкездейсоқ сандардың генераторларын қолданатын болсақ, хаттама қаскүнем бұл генераторды бұза алмайды деген шарт болған жағдайда ғана қауіпсіз болады. Мұндай хаттама есептеулер бойынша қорғалған (computationally secure) деп аталады. Бұл айырмашылықтың толық білетін теоретиктер үшін ғана мағынасы болады. Барлық криптографиялық хаттамалар көбіне арқашан есептеуіш жақындалуға негізделген. Бұндай жақындалудың нақты бір шабуыл түріне байланысты шығарылуы жақсы жақсаруға әкелмейді. Сонымен қатар, сөзсіз сақталуды қамтамасыз етуге қажетті ақиқат кездейсоқ сандардың шығаруы соншалықты қиын, мұндай сандарды қолдану әрекеті жүйенің қауіпсіздігін тек бұзуы мүмкін. Ақиқат кездейсоқ сандардың генераторының кез-келген нашар орны қауіпсіздіктің жоғалуына әкеліп соғады. Басқа жағынан қарағанда, егер ақиқат кездейсоқ сандарды жалғанкездейсоқ сандардың генераторына бастапқы санды табу үшін ғана қолдансақ, онда өзімізге әр түрлі энтропиялардың көздерін қолдануды жасай алу, сөзсіз, біздің расында да қауіпсіз жүйені құруымыздың мүмкіндіктерін көтереді.

1. 4 Жалғанкездейсоқ сандардың генераторына шабуылдардың моделдері.

Жалғанкездейсоқ сандардың генераторлары салыстырмалы аз зерттелген. Кездейсоқ (жалғанкездейсоқ) сандардың генерациясының шарты кейбір бастапқы санның негізінде біраз жеңіл. Мәселе кездейсоқ санды қайдан алу және оны қалай құпия сақтауда болып отыр. Бұл мәселенің ең жақсы шешімі болып қазіргі кезде бізге белгілісі Yarrow деп аталатын генераторы табылады. Бұл белгілі шабуыл түрлерінен жүйені қорғауға тырысып жатқан жалғанкездейсоқ сандардың генераторы бізбен Джон Келсимен (John Kelsey) бірге бірнеше жыл бұрын жасалынып шығарылған.

Уақыттың әрбір сәтінде жалғанкездейсоқ сандардың генераторында ішкі күйі бар. Кездейсоқ сандарды алудың сұранымдары жалғанкездейсоқ сандарды генерациялайтын криптографиялық алгоритммен қызмет етіледі. Бұл алгоритм, сонымен қатар, генератор келесі жолы осы кездейсоқ сандарды шығармауды кепілдеу үшін генератордың ішкі күйін жаңартады. Бұл процесс онша қиын емес; осы тапсырмаларды орындауды кез-келген кэштау функциясы немесе блоктық шифр істей алады.

Жалғанкездейсоқ сандардың генераторларына шабуылдаудың әр түрлі формалары бар. Бәрінен бұрын қаскүнем генератордың ішкі күйін оның шығыс мәліметтеріне негізделе отырып құрғысы келіп тырысатын тура шабуылды атап өту керек. Бұл қазіргі заманғы криптографиялардың әрекеттерін қолдана отырып өте оңай қарсы тұруға болатын криптошабуылдың классикалық түрі.

Егер қаскүнем қандай да бір этапта генератордың ішкі күйін ала алатын болса, жағдай нашарлайды. Қазір бізді оның қалай болатыны қызықтырмайды. Мүмкін ақпарат шығысы бағдарламалық қамтамасыздандырудың қандайда бір қателігінен, немесе компьютер бірінші рет жүктелгендіктен әлі кездейсоқ бастапқы саны болған жоқ, немесе, айталық, қаскүнем бастапқы санның файлын дискіден оқып алды. Барлық осы жағдайларда генератормен өте жаман нәрселер бола бастайды. Егер қаскүнем жалғанкездейсоқ сандардың классикалық генераторларының ішкі жағдайын біле алатын болса, ол барлық келесі шығыс мәліметтерінің және барлық ішкі күйдің жаңартуларының мәндерін жүргізе алады. Осыдан шығатыны, егер жалғанкездейсоқ сандардың генераторына шабуылдың қандай да бір уақытта сәтті аяқталатын болса, бұл генератор ешқашан қауіпсіз жағдайға келе алмайды.

Қаскүнемге ішкі күйі белгілі генератордың қауіпсіздігін қайта құру өте қиын. Ол үшін ақиқат кездейсоқ сандарды генерациялауға болатын қандай да бір энтропия көзі керек болады. Жеңілдік үшін бізде уақыттың болжамсыз кезінде энтропияның керекті санын беретін бір немесе бірнеше көздер бар деп есептейміз (әдетте оқиғалар деп атайтын бірнеше үлестер түрінде) .

Тіпті егер біз генератордың ішкі күйін оқиғалардың шығуы кезінде пайда болған энтропияның бірнеше санымен араластырсақ та, қаскүнемде әлі де шабуыл жолдары болады. Ол генераторға кездейсоқ мәліметтерді алу туралы жиі сұраныстар жібере алады. Осындай екі сұраныстың арасындағы уақыт аралығында генератордың ішкі күйіне қосылатын энтропиялардың жалпы саны, айталық, 30 битпен шектелген болғандықтан қаскүнем жай ғана кездейсоқ кіріс мәліметтерінің мүмкін нұсқаларын қолданып шыға алады және аралыстырудан кейін алынған жаңа ішкі күйді анықтай алады. Бұл қазіргі заманғы технологиялардың көмегімен мүмкін болатын 2 ³⁰ жуық қадам керек. Дұрыс шешімді тапқаннан кейін қаскүнем генератормен берілетін сол алдыңғы кездейсоқ мәліметтердің көмегімен оңай тексере алады.

Аталған шабуыл түрімен күресу үшін жасауға болатын әрекеттердің ең жақсысы - бұл энтропиясы бар кіріс оқиғалардың тобын ұйымдастыру. Біз энтропияларды қаскүнем жинаған кездейсоқ мәліметтерді біз энтропияларды аралыстарған кезде болжай алмайтындай жағдайға жеткенше жинаймыз. Сонымен, ол үшін қанша энтропия керек болады? Біздің қауіпсіздік деңгейіне деген сұранысымызға байланысты қаскүнем шабуыл жасау үшін кем дегенде 2 ¹²⁸ қадам жіберуі керек, ол үшін 128 бит энтропия керек. Бірақ бұл жерде біз маңызды бір мәселеге кезігеміз: энтропия санының қандай да бір бағалауын алу тіпті мүмкін болған жағдайда да өте қиын. Энтропияны бағалау қаскүнемнің қанша білуіне немесе білу мүмкіндігіне байланысты айтарлықтай тәуелді болады, ал бұл ақпарат жүйе құрастырушыларына құру кезеңінде әлі белгісіз. Міне, Yarrow генераторының мәселесі осында тұр. Ол энтропияны бағалауды қолдана отырып көздің энтропиясын есептеуге тырысады, ал барлық жағдайлар үшін дұрыс бағалауды алу практика жағынан мүмкін емес.

Жүйе құрастырушылары осы бөліммен жұмыс жасаған кезде Yarrow генераторын жетілдірген. Жаңа шешім Fortuna (Фортунаның атына - соқыр жағдай мен сәттің ежелгіримдік құдайының атына) деген атқа ие болды. Fortuna энтропияны бағалаудан бас тарта отырып оны анықтау керегінің мәселесінен шығарды. Әрі қарай көбінесе ЖКСГ (жалғанкездейсоқ кездейсоқ сандар генерациялау) Fortuna-ның толық қарастыру туралы айтылады.

Fortuna үш бөліктен тұрады. Генератор бекітілген ұзындықтың бастапқы санын кіріске алады және жалғанкездейсоқ мәліметтердің кез келген санын береді. Аккумулятор әр түрлі көздерден энтропияларды жинап толтыра бастайды, сонымен қатар генератордың бастапқы санын уақыт арасында өзгертіп отырады. Және ақырғысы, бастапқы санның файлының басқару жүйесі генератор кездейсоқ мәліметтерді тіпті компьютердің қайта жүктеуінен кейін де шығара алатынына кепіл береді.

2 Кездейсоқ сандар генераторының тәжірибеде іске асырылуы

2. 1 Кездейсоқ сандар генераторының құралдары

Генератор белгіленген ұзындықтың кейбір жағдайын кез келген ұзындықтың шығыс мәліметтеріне ауыстырады. Генератор ретінде біз AES-ұқсас блоктық шифрды қолданамыз. Өздеріңізге ұнайтынын таңдаңыздар - AES (Rijndael), Serpent немесе Twofish. Генератордың ішкі күйінде 256-биттік блоктық шифрдың кілті және 128-биттік есептеуіш болады.

Өзінің мәні бойынша генератор - бұл тек қана есептеуіш жағдайында жұмыс жасайтын блоктық шифр. Еске салайық, есептеуіш жағдайы немесе CTR мәліметтердің біз шығыстар ретінде қолданатын кездейсоқ ағынын генерациялайды. Қауіпсіздікті жоғарылату үшін блогтық шифрдың жұмыс режиміне тағы бірнеше жетілдірулерді қосамыз.

Егер қолданушы немесе қосымша кездейсоқ мәліметтер сұрайтын болса, генератор өзінің алгоритмін қосып жалғанкездейсоқ мәліметтер шығарады. Енді қаскүнем генератордың күйін кезекті сұраныстан кейін алуға мүмкіндігі болсын деп есептейік. Егер генератормен берілген алдыңғы нәтижелер дескридитацияланбаса жақсы болар еді. Ол үшін әрбір сұраныстан кейін тағы 256 бит жалғанкездейсоқ мәліметтерді генерациялаймыз және оларды шифрлаудың жаңа кілті ретінде қолданамыз. Ескі кілт осы кезде алдыңғы сұраныстар туралы ақпараттың шығуын болдыртпау үшін жойылады.

Генерацияланған мәліметтер статистикалық кездейсоқтыққа ие болуы үшін бір мезгілде аса көп мәліметтерді генерациялап керегі жоқ. Расында да, ақиқат кездейсоқ мәліметтерде блоктың мәндері қайталануы мүмкін, ал есептеуіш режиміндегі шығыс мәліметтері ешқашан қайталанатын блоктарды шығармайды. Бұл мәселені шешудің бірнеше жолдары бар. Мысалы, практика жағынан блогтың ақиқат кездейсоқ кезегінен статистикалық ауытқуын болдырмайтын тексті шифрлаудың блогының тек бір жартысын қолдануға болады. Блогтық шифрлаудың орнына екінің бірі ретінде жалғанкездейсоқ функцияны (pseudorandom function) қолдануға болады, бірақ бізге әлі жақсы зерттелген және тиімді ұсыныстар кездескен жоқ. Осы жағдайда жасауға болатындардың ең оңайы - ол бір сұранысқа берілетін кездейсоқ мәліметтердің байт санын шектеу. Бұл ақиқат кездейсоқ кезектіктен статистикалық ауытқуын қиындатады.

Егер бізге 2 ⁶⁴ мәліметтер блогын бір ғана кілттің көмегімен генерациялау керек болатын болса, біз блоктардың мәндерінің арасында қайшылықтардың пайда болғанын күтер едік. Осындай өлшемді сұраныстардың бірнеше қайталаулары генератордың шығыс мәліметтері ақиқат кездейсоқ емес екендігін тез көрсетер еді; оларға қайшылықтардың санының күтілімі жетпейді. Сондықтан біз бір сұранысқа берілетін мәліметтердің максималды өлшемін 2 ¹⁶ блоктармен (яғни, 2 ²⁰ байт) шектейміз. Кездейсоқ сандардың тамаша генераторы үшін 2 ¹⁶ мәліметтер блогтарының арасынан қайшылықтардың табылу ықтималдығы жуықтап 2 ^-97 құрайды, сондықтан қайшылықтың толық жоқтығы жуықтап 2 ⁹⁷ сұраныс жасағаннан кейін ғана табылуы мүмкін. Қаскүнемге жасауға керекті жұмыстың жалпы саны жуықтағанда 2 ¹¹³ қадамды құрайды. Бұл, әрине, біз ойлағандай 2 ¹²⁸ қадамнан аз, бірақ сонда да онша жаман емес.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.