Математикалық модель құру

Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 25 бет
Таңдаулыға:

Мазмұны

1. КІРІСПЕ
2. НЕГІЗГІ БӨЛІМ
. 2.1 Есептің қойылымы
. 2.2 Математикалық модель құру
. 2.3 Есепті шығарудың нақты әдісі
. 2.4 Есептің шешімі
. 2.5 Есептің блок – схемасы
. 2.6 Есептің бағдарламасы (бағдарлама листингі)
. 2.7 Программаны баяндау бөлімі
3. ҚОРЫТЫНДЫ
ҚОЛДАНЫЛҒАН ӘДЕБИЕТТЕР

1. КІРІСПЕ

Адамзат баласы өте ертеден объектерді, процестерді, әр түрлісаладағы
құбылыстардызерттеу барысында модельдеу тәсілін қолданып келеді.
Осы зерттеулердің нәтижелері нақты объектілермен процесстердің
қасиеттерін анықтауда, құбылыстардың болу себептерін ашуда, жаңа
объектілерді құрастырумен ескілерін таңдауда және т.б. маңызды орын алады.
Модельдеу адамның өз іс-әрекетін алдын-ала жоспарлап, дұрыс шешім
қабылдануына әсер етеді.
Адам қолмен абстракты немесе материалды обьектілер модельбола алады.
Модельді талдау нәтижесінде шын мәніндегі күрделі объектіні тереңірек
білуге мүмкіндікгі туады. Мұндағы шын мәніндегі нағыз табиғи объект, яғни
нақты объект прототип немесе жұп нұсқа деп аталады.
Модель дегеніміз – нақты объектіні процессті немесе құбылысты ықшам
әрі шағын түрде бейнелеп көрсету. Модельдеу – объектілерді, процестерді
немесе құбылыстарды зерттеу мақсатында олардың модельдерін құру.
Объектілердің модельдері ретінде әбеди шығармалар немесе архитектуралық
ғимараттың кішірейтілген көшірмесі, мектептегі оқу құралдары т.б. болуы
мүмкін. Модельсутегі атомы, күн жүйесіндегі планеталар, елдегі парламент
үкіметінің т.б. нақты өмірде бар дүниені бейнелеуі мүмкін. Бірақ модель
ретінде нақты өмірде бар дүниені бейнеленуі мүмкін. Бірақ модель ретінде
нақты бір заттың абстракты қорытындысын көрсетуге болады. Процесстердің де
модельдерін құруға, яғни материалдық объектімен жасалатын іс-әрекеттерді
модельдеуге болады. Оған мысал ретінде эканомикалық немесе экологиялық
процестерді, бүкіл әлемнің немесе қоғамның дамуын модель арқылы
айтуғаболады. Модель көрнекті түрдежазбаша жоспар, сызба ретінде жасалуы
мүмкін. Бір объекті үшін әр түрлі модельдер жасалуы мүмкін.
Модель – көрнектi түрде, жазбаша жоспар, сызба түрiнде жасалуы мүмкiн.
Мұндай модельдер бiздiң ойымызда бейнеленетiн прототип пайда болғанға дейiн
жасалады. Кез – келген объект үшiн әр түрлi модельдер жасалуы мүмкiн.
Модельдiң жасалуы зерттеу мақсатында және прототип жөнiнде жинақталған
мәлiметтердiң көлемiне тәуелдi болады.

Модельдiң түрлерi
Модельдердi қасиеттерiне байланысты мынадай топтарға жiктеймiз:
1. Қолданылу аймағы;
2. Модельдiк уақыт факторын ескеру;
3. Бiлiм саласына қарай топтау;
4. Модельдi көрсету тәсiлiне қарай топтау.
1) Қолданылу аймағына байланысты модель – оқу, тәжiрибелiк, ғылыми –
техникалық, ойын және имитациялық болып беске бөлiнедi.
Оқу модельдерi – көрнектi оқу құралы, әр түрлi жаттықтырушы және
үйретушi программалар түрiнде болады.
Тәжiрибелiк модель – жобалау объектiсiнiң кiшiрейтiлген немесе өте
кiшкентай объектiлер үшiн олардың үлкейтiлген көшiрмесi болып табылады. Бұл
модельдер объектiлердi зерттеп, қасиеттерiн болжау, зерттеу мақсатында
қолданылады.
Ғылыми – техникалық модельдер – процестер мен құбылыстарды зерттеу
мақсатында жасалады.
Ойын модельдерi - әскери, экономикалық спорттық ойындар жатады. Бұл
модельдер әр түрлi жағдайда объектiнi бақылауға жаттықтырады. Ойын
модельдерi әр түрлi жағдайда адамға психологиялық көмек көрсетедi.
Имитациялық модель – шын мәнiндегi нақты объектiнi өте жоғары дәлдiкпен
бейнелей алады. Тәжiрибе нақты объектiнi зерттеу, бағалау мақсатында
бiрнеше рет қайталанады немесе бiр мезгiлде әр түрлi жағдайларда
жүргiзiледi. Дұрыс шешiмдi таңдаудың мұндай тәсiлi – байқау әдiсi деп
аталады.
Модельдi уақыт факторына байланысты динамикалық және статистикалық деп
екi топқа бөлемiз.
Статистикалық модель деп – объект жөнінде алынған ақпараттың белгілі
бір уақыт бөлігіндегі уақыт үзіндісін айтамыз.
Динамикалық модель – уақыт барысындағы объектінің қасиеттерінің
өзгерістерін көрсету мүмкіндігін береді.
Модельдерді көрсетілу әдісіне байланысты, материалдық және
ақпараттық деп 2 топқа бөлеміз.
Ақпараттық модель екіге бөлінеді: таңбалық және вербальдік.
Таңбалықтың өзі екіге бөлінеді: компьютерлік модель және компьютерлік
емес модель.
Курстық жұмыстың негізгі мақсаты болып - өндірістегі берілген өнім
түрлерін өндіруден түсетін өнімнің максималды табысын есептейтін
бағдарлама әзірлеп оны сызықтық программалау есебінің симплекс әдісімен
шешіп және осы әдіспен шешілетін есепті ЭЕМ-нің көмегімен шешуге болатындай
етіп бағдарламаны әзірлеу.

НЕГІЗГІ БӨЛІМ
2.1 Есептің қойылымы
Эффектілік критерийлердің саны бойынша математикалық модельдер бір
критерлік және көпкритерлік деп бөлінеді, яғни екі немесе одан да көп
критерийдан тұрады.
Белгісіз факторлар бойынша математикалық және белгісіз элементі бар
модельдер деп бөлінеді.
Стохастикалық модельде белгіңіз факторлар – бұл кездейсоқ өлшемдер,
бұлар үшін белгілі функцияларды бөлу және әртүрлі стохаестикалық сипаттар
(математикалық тосу, дисперсия, орташа ауытқу және тағы басқа).
Олардың арасынан мыналар бөлінеді:
1) стохастикалық бағдарламалау моделі, оларға мақсатты функцияға шектеулі
түрде кездейсоқ өлшемдер кіреді;
2) кездейсоқ процестер теориясының модельдері, олар процесстерді
зерттеуге арналған, оның жағдайы әр уақытта кездейсоқ көлемде болады;
3) тұтас қызметкөрсету теориясының модельдері, оларда көпканалды жүйелер
шектеледі.
Белгісіздік элементі бар модельдер факторларға тәуелді жағдайларды
модельдеуге қолданылады, олар үшін статистикалық мәліметтерді жинау мүмкін
емес және олардың маңызы белгсіз:
1. ойын теориясының моделіне тапсырма ойын түрін беріледі, онда бірнеше
ойыншылар қатысады, әртүрлі мақсатты көздейтін;
2. имитациялық модельде шынайы процесс машиналық уақытта болып жатады;
3. детерминалық модельдер белгісіз фактор есепке алынбайды. Оларға
көптеген экономикалық міндеттер қосылады. Мақсатты функция түрімен
шектеулі детерминалық модельдер сызықтық, сызықсыз, динамикалық және
графикалық деп бөлінеді:
1. сызықтық модельде мақсатты функция жәнек ауыспалы басқару бойынша
шектеулі сызықты;
2. сызықсыз модель – мұнда не мақсатты функция не қандайда бір шектеулер,
не болмаса барлық ауыспалы басқару бойынша сызықсыздар шектеулі;
3. динамикалық модельді уақыт факторы есепке алынады;
4. графикалық модель тапсырманы графикалық құрылым түрінде көрсетуге
қолайлы болғанда қолданылады;
1) өзіндік құнды өндірудің минимизациясы
2) өңдеу уақытының минимизациясы
2. Модельдердің параметрлері:
1. m – жабдықтау бірліктерінің саны;
2. n - кәсіпорын шығара алатын бұйым атауларының саны;
3. Ті – жұмыс уақытын фонды і-жабдықтау бірліктері, i=1,m;
4. lk – бұйым жасаудың әртүрлі әдістер саны k-нің атауы, әртүрлі
уақытпен сипаттаушы өңдеудің жадбықтау бірлігінде i –ші типті k =1, n;
5. tikl – бұйым өңдеудің уақыты k-нің атаулары, жасалған l - м
жабдықтау әдісімен i –ші типті i=1,m; k=1,n; l=1,lk
6. αk – бұйымға сұраныс k-нің атаулары k =1, n;
7. S – алдын-ала ескерілгенді бұйымдардың сақталуына арналған складтың
размері;
8. ckl – бұйымның өзіндік құны k-ның атаулары l әдісімен k =1, n;
l=1,lk.
9. ckl – талап етілетін бұйымның өзіндік құны k атауының
10. Басқаратын айнымалылар:
3. Мүмкін болатын шешімдердің анықтамасы
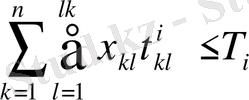жабдықтау жұмыс фондының шектеулері.
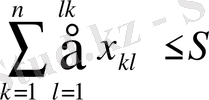- склад размері бойынша шектеулер.
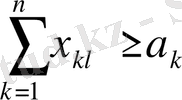- сұраныс бойынша шектеулер;
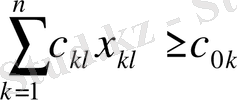- өндірудің өзіндік құнының шектеулері
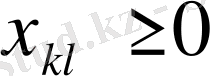
4. Басқару айнымалылары және параметрлері бойынша өзгерту критериясының
нәтижесі
1) Пайданың максимизациясы:
П – пайданың қосындысы:
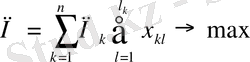, Пк – k атаулы 1 бұйым өткізудің пайдасы
2) Өзіндік құнның минимизациясы:

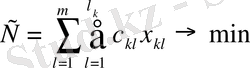
3) Станко сағаттарда көрсетілген Т өңдеудің уақыт қосындысының
минимизациясы:

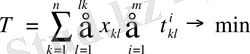
4) Өңдеу уақытының қосындысының минимизациясы:

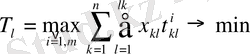
Біз бір көп критерийлі немесе төрт біркритерийлі сызықтық модель
құрдық.
Егер сызықты емес пайда шығарылатын бұйымдардың санына тәуелді болса,
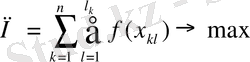, мұнда f – кейбір сызықтық емес функция, негізгі мақсат
шешімдерімен, ұсынылған модельдерден кез-келген есептің нәтижесінде,
қисынға келгендерді қанағат етсе және бірнеше оптималды критерийлерді
немесе бір экстремумды қанағат ететін xkl айнымалы мәніне қызмет етеді.

Тапсырма
Институт 4 іздестіру проектілерін орындауға грант алды. 1-ші проектің
шығу мәні 2-ші проект үшін кірістірілген мәлімет болып табылады, 2-ші
проектің шығу мәні 3-ші проект үшін, 3-ші проектің шығу мәні 4-ші проект
үшін кірістірілген мәлімет. Проектінің ғылыми жетекшісі ретінде әртүрлі
тәжірибесі бар 4 ғалымның кандидатурасы қарастырылады. Әр ғалым өзіне
проектіні орындау үшін қажет уақытты бағалайды.

Уақыт матрицасы:
Мұнда әр ғалымға аймен берілген жұмыстың ұзақтығы көрсетілген. Барлық
проектіні орындағандағы уақыттың қосындысы минималды болатын, әр проектінің
ғылым жетекшісін таңдау қажет.

2.2 Математикалық модель құру
Математикалық модель есебін құрайық:
1. Есептің мақсаты: барлық орындалған проектінің уақыт қосындысын
минималдау
2. Параметрлері есептің шартында берілген
3. Айнымалылардың басқармасы
4. Мақсатты функция

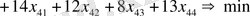
2.3 Есептi шығарудың нақты әдiсi

Тағайындау есебі Т.Е.Венгер әдісімен шешілуі мүмкін.
Тағайындау есебін шешу үшін кесте құрамыз.
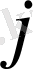1 бағанға жұмысқа кандидат номерін, ал 1 жолға жұмыс номерін жазамыз.
Венгер әдісінде принцип қолданылады: тағайындау есебінің оптималды шешімі
жолдағы(бағандағы) элементтің мөлшерін кішірейткенде(үлкейткенде)
өзгермейді.
Әдіс алгоритмі:
1. Әр жолдан нөлді алу. Ол үшін әр жолдан ең кіші элементті іздейді және
осы жолдың барлық элементтерінен мәні алынып тасталынады.
2. Әр бағаннан нөлді алу. Жаңа кестенің әр бағанынан минималды элементті
іздейді және осы бағанның барлық элементтерінен мәні алынып
тасталынады.
3. Оптималды шешімді іздеу.Нөлі аз жолды қарастырады. Осы жолдағы нөлді
белгілейді және осы жол мен бағандағы қалған басқа нөлді сызып
тастайды. Осылай барлық жолдармен жүріп шығамыз. Егер белгіленген
нөлдер n-ға тең болса, онда шешуі оптималды болады. Қарсы жағдайда 4-
ші пункте көшеміз.
4. Нөлдері бар жолдар мен бағандардың минималды жинағын іздеу. Ол үшін
келесілерді белгілеп қою қажет:
a) Белгіленген нөлдері жоқ барлық жолдарды;
b) Белгіленген жолдың біреуінде болсын сызылған нөлі бар барлық
бағандарды;
c) Белгіленген бағанның біреуінде болсын сызылған нөлі бар барлық
жолдарды;
b және с қимылдары белгілейтін жол мен бағанбіткенге дейін кезекпен
қайталана береді. Сондықтан әрбір белгіленбеген жол мен белгіленген бағанды
сызып отыру қажет.

5. Кейбір нөлдерді ауыстыру. Түзу өткізілген торлардан ең кіші сандарды
алу. Осы санды сызылмаған бағанда тұрған әр саннан алып және сызылған жолда
тұрған әр санға қосамыз.

6. Есептің мақсаты: барлық орындалған проектінің уақыт қосындысын
минималдау
2.4 Есептің шешімі
Параметрлері есептің шартында берілген
Мақсатты функция:

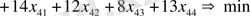
a. Әр жолдан минималды элементті тауып, оны осы жолдың әр
элементінен алып тастаймыз.

№ 1 2 3 4 min
1 8 12 10 13 8
2 7 9 9 10 7
3 9 12 7 13 7
4 14 12 8 13 8

№ 1 2 3 4
1 0 4 2 5
2 0 2 2 3
3 2 5 0 6
4 6 4 0 5

1. Әр бағаннан минималды элементті тауып, оны осы жолдың элементінен алып
тастаймыз.

№ 1 2 3 4
1 0 4 2 5
2 0 2 2 3
3 2 5 0 6
4 6 4 0 5
min 0 2 0 3

№ 1 2 3 4
1 0 2 2 2
2 0 0 2 0
3 2 3 0 3
4 6 2 0 2

1-ші жолдағы нөлді белгілеп, 1-ші бағандағы қалғандарын сызып
тастаймыз. 2-ші жолда 2-ші бағандағы 1-ші сызылмаған нөлді белгілейміз және
2-ші жолдағы мен 2-ші бағандағы белгіленбеген және сызылмаған нөлді сызып
тастаймыз. 3-ші жолда нөлді белгілеп, 3-ші бағандағы нөлді сызамыз.
Белгіленген нөлдер саны 34 –ке тең, шешім оптималды емес, сондықтан келесі
4-ші пунктке көшеміз.
№ 1 2 3 4
1 0. 2 2 2
2 0 0. 2 0
3 2 3 0. 3
4 6 2 0 2

2. – ші бағанда белгіленген ноль бар, 3 – ші жолда сол жолды белгілейік.
Енді жоқ бағандар, құрылымдағы нольдері сызылып, белгіленген жолдарды
өшіреміз. Белгіленген бағандарды және белгіленбеген жолдарды

№ 1 2 3 4
1 0. 2 2 2
2 0 0. 2 0
3 2 3 0. 3
4 6 2 0 2

5.Қалған клеткадағы элемент 2 – ге тең. 2 – ні шығарамыз, әр біруіне
сызылмаған баған сандары.
№ 1 2 3 4
1 0 2 4 2
2 0 0 4 0
3 0 1 0 1
4 4 0 0 0

№ 1 2 3 4
1 -2 0 2 0
2 -2 -2 2 -2
3 0 1 0 1
4 4 0 0 0

Берілген таблицаны 3 қадамды қайталайық.
Белгіленген нольдер саны 4 тең. Осылайша біз оптималды шығуын аламыз. 1
– ші ғалым 1 – ші проектіні басқарады, 2 – ші ғалым 2 – ші проектіні, 3 –
ші ғалым 3 – ші проектіні, 4 – ші ғалым 4 – ші проектіні.
№ 1 2 3 4
1 0. 2 4 2
2 0 0. 4 0
3 0 1 0. 1
4 4 0 0 0.

Проектіні шығару уақыты:
Т=8+9+7+13=37ай

2.5 Есептің блок - схемасы

2.6 Есептің бағдарламасы (бағдарлама листингі)
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls,
Forms,
Dialogs, StdCtrls, Grids, ExtCtrls, Buttons;
type
TForm1 = class(TForm)
SG1: TStringGrid;
Label2: TLabel;
Panel1: TPanel;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Edit4: TEdit;
Edit5: TEdit;
Edit6: TEdit;
Edit7: TEdit;
Edit8: TEdit;
Edit9: TEdit;
Edit10: TEdit;
Edit11: TEdit;
Edit12: TEdit;
Label3: TLabel;
BitBtn1: TBitBtn;
Edit21: TEdit;
Edit22: TEdit;
Edit23: TEdit;
Edit24: TEdit;
Button3: TButton;
Edit25: TEdit;
Edit26: TEdit;
Edit27: TEdit;
Edit28: TEdit;
Button4: TButton;
Button5: TButton;
Button6: TButton;
Button1: TButton;
procedure FormCreate(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button4Click(Sender: TObject);
procedure Button5Click(Sender: TObject);
procedure Button6Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
x1,x2,x3,x4,y1,y2,y3,y4,z1,z2,z3,z4 ,v1,v2,v3,v4,x11,x12,x13,x14,y11,y1 2
,y13,y14,z11,z12,z13,z14,v11,v12,v1 3,v14, min:integer;
implementation
uses Unit2;
{$R *.dfm}

procedure TForm1.FormCreate(Sender: TObject);
begin
SG1.Cells[0,0]:='N';
SG1.Cells[0,1]:='1';
SG1.Cells[0,2]:='2';
SG1.Cells[0,3]:='3';
SG1.Cells[0,4]:='4';
SG1.Cells[1,0]:='1';
SG1.Cells[2,0]:='2';
SG1.Cells[3,0]:='3';
SG1.Cells[4,0]:='4';
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.