Тұрақты ток электр тізбектерінің теориясы мен есептеу әдістері


Мазмұны
кіріспе
1 ТҰРАҚТЫ ТОҚТЫҢ ЭЛЕКТР ТІЗБЕКТЕРІ
1. 1 Негізгі ұғымдар мен анықтамалар
1. 2 Тұрақты тоқ электр тізбектерінің заңдары
2 Контурлық токтар әдісі
2. 1 Контурлық токтардың матрица түрінде құрылған теңдеулері
2. 2 Беттестіру принципі
2. 3 Түйіндік әлеуеттер әдісі
2. 4 Екі түйіндік әдіс
қорытынды
пайдаланған әдебиеттер
қосымша
3
5
5
7
8
9
12
15
20
22
23
Кіріспе
Қазіргі уақытта электр энергиясы барлық өнеркәсіп салаларында, транспортта, ауыл шаруашылығында, үй тұрмысында, тағы да басқа халықтың тұрмыс қажетіне кеңінен пайдаланылады. Осы курстың негізгі бір міндеті, ол құбылыстарды токтар, кернеулер, қуаттар, магнит ағындары т. б. түсініктер арқылы есептеу, зерттеу. Сондай - ақ тағы бір атқаратын міндеті, ол әрбір құбылыстарды электр кернеулігі, магнит өрісінің индукциясы, қуат ағындары, т. б. түсініктер арқылы есептеу, зерттеу. Осы міндеттердің біріншісі тізбектерді есептеу мен зерттеуге, ал екіншісі электр магниті өрістерін есептеуге, зерттеуге арналған.
Электр техникасының өсіп-дамуы электр магниті құбылыстарын жете зерттеуді, оқып білуді, практика жүзінде пайдалануды керек етеді. Осы зор еңбекте, ізденуде, көптеген жаңалықтарды ашуда орыс инженерлерінің, ғалымдарының қосқан үлесі аз емес. Олар шет елдердің көрнекті ғалымдарымен бірлесе отырып электр техникасының маңызды салаларының бастамасына жол ашты. Осы бастаманы бастағандардың бірі - М. В. Ломоносов. Ол атмосфера электрі атты теориясын құрды.
Электр және магнит тізбектерін шешудегі теориялық мәселелері мен қатар практикалық электр техникасында электр магниттік өрістерді есептеу жайындағы мәселелері де алдыға қойды. Электр машинасының тетіктерін және электр магниттік аппараттарды құрастыру үшін магнит өрістерін есептеу қажет болды. Ток өткізгіштерін тұрғылықты түрде изоляциялау үшін оқшаулаушы материалдарды табу керек болды және электр өрісін есептеу мақсаты да алдыға қойылды.
Қазақстанда жүргізілуіне байланысты электр энергэтика саласын кеңінен дамыту қажет болды. Соның салдарынан Қазақстанда электр энергетиканың ең көп дамыған республиканың біріне айналды. Сондықтанда Советтер одағында үшінші энергэтикалық институты Алматыда ашылды.
Жалпы тербелулердің жиілігінің сәйкес келуі, сырттан келген физикалық жүйенің хабарлануы, сонымен қатар осы жүйенің меншікті еркін тербелуінің жиілігі резонанс деп аталады. Электр тізбегінде резонанс меншікті еркін тербелу жиілігі мен айнымалы ток жиіліктерінің сәйкес келуі арқасында пайда болады.
Индуктивтілік пен сыйымдылықтан тұратын, тізбек, тербелмелі контур болуы да мүмкін, сонымен қатар жүйк бола алады, сол мезетте тізбекте сыйымдылықтың тербелмелі разряды индукцияға өту құбылысын көре аламыз. Егер сыйымдылық алдымен бастапқы кернеулікке U Н дейін зарядталып, ал содан соң индуктивті тұйықталса, онда контурда разрядты ток i бірте-бірте өсіп келе жатқаны көрінеді. Токтың күші ақырындап өсуі керек, себебі оның өсуіне электр қозғаушы күшінің өздік индукциясы қарсылық көрсетеді e L =-Ldi/dt .
Екіұштыға бір немесе бірнеше индуктивтік және бір немесе бірнеше сыйымдылық кірсін делік. Сонда екіұштыдағы резонанс кезіндегі істелген жұмысты былайша ұғуға болады. Екіұштының кірер кедеогісі резонанс кезінде актив кедергісі болып келеді де, кірер ток пен кернеу фаза бойынша бір-біріне дәл үйлесіп келеді, ал сонда реактив кедергілері шама жағынан бір-біріне тең болады және фаза бойынша бір-біріне қарама-қарсы. Сондықтан реактив қуаты осы екіұштыда нөлге тең. Осындай екіұштының резонанс кезіндегі жұмысын екіштының резонанс тәртібі деп атайды.
Резонанс режимінің негізгі екі түрі кездеседі - кернеу резонансы және ток резонансы.
1 ТҰРАҚТЫ ТОҚТЫҢ ЭЛЕКТР ТІЗБЕКТЕРІ
- Негізгі ұғымдар мен анықтамалар
Электрмен зарядталған бөлшектердің бағытталған қозғалысы электр тоғы деп аталады. Металлдарда - электрондар, ал сұйықтарда - иондар тоқтың жүруіне негіз болады. Уақыт аралығында шамасы мен бағыты өзгермейтін тоқты тұрақты тоқ деп атайды.
Электр тізбегі деп бір-бірімен жалғастырылған электр энергиясы көздерінен жəне оның қабылдағыштарынан тұратын тізбекті айтады. Сол сияқты, электр энергиясын энергия көздерінен қабылдағыштарға беру үшін арналған коммутациялық тетіктері, өлшеуіш аспаптар жəне жалғаушы сымдар электр тізбегіне жатады.
Электр энергиясы көздерінде басқа энергия түрлері электр энергиясына айналады.
Тұтынушыларда электр энергиясы энергияның басқа (жылу, жарық, механикалық т. б. ) түрлеріне айналады.
Электр тізбегін график түрінде көрсету - электр схемасы деп аталады.
Шартты белгілер арқылы бейнеленген электр схемасы - принциптік электр схемасы деп аталады.
Электр тізбегі тармақ, түйін жəне контур деген ұғымдармен сипатталады.
Тармақ деп бойымен бір ғана тоқ жүретін электр тізбегінің бөлігін атайды.
Түйін деп үш немесе одан да көп тармақтар тоғысатын электр тізбегінің нүктесін атайды.
Контур деп құрамына бір-бірден тармақ пен түйін кіретін тұйық тізбекті айтады. Контурлардың тəуелді жəне тəуелсіз түрлері болады.
Тəуелсіз контурда басқа контурлар құрамына кірмейтін кем дегенде бір тармақ болады.
Энергия көздерінде энергияның электрлі емес түрін электрлі түріне айналдыру процесінен электр қозғаушы күші (ЭҚК) Е пайда болады. Осы ЭҚК-і тұйық тізбекте электр тоғын тудырады.
1. 1 а, б-суретте ЭҚК-тің схемаларда шартты белгіленуі көрсетілген.

а) б)
- - сурет
Энергияны өзгерту кезінде энергия көздерінде шығындар болады.
Осы шығындар ішкі кедергілермен R
 анықталады.
анықталады.
Тоқ күші деп - уақыт бірлігінде өткізгіштің көлденең қимасы
арқылы өтетін электр энергиясының мөлшеріне тең скалярлық шаманы атайды:
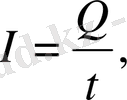
мұндағы Q - электрдің мөлшері; t - уақыт.
Тоқ ампермен өлшенеді, (А) .
Электр тоғының бағыты үшін оң зарядтардың реттелген
қозғалысы қабылданған.
Электр тоғының бағыты схемаларда жебемен (стрелкамен) көрсе-
тіледі (1. 2-сурет) .
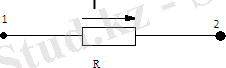
- - сурет
Берілген нүктедегі өрістің потенциалы ϕ деп нүктелік оң зарядты шексіздіктен осы нүктеге алып келу үшін жасалатын жұмысқа тең шаманы айтады:
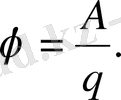
Кернеу (кернеудің түсуі) деп нүктелік оң заряд тізбек бөлігі
бойымен қозғалғанда жасалатын толық жұмысқа сандық мəні тең
шаманы айтады:
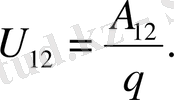
Кернеу вольтпен өлшенеді, (В) .
Тізбек бөліктерінің ұштарындағы кернеу "1" жəне "2" нүктеле-
ріндегі потенциалдар айырмасына тең:
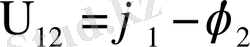
Тізбек бөлігінің электр кедергісі (кедергі) R деп берілген тізбек бөлігіндегі зарядтардың реттелген қозғалысын анықтайтын қасиетті айтады.
Резистор деп кедергілік қасиеті бар электротехниалық құрылғыны айтады.
Электр кедергісіне кері шаманы электр өткізгіштігі (өткізгіштік) G деп атайды:
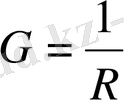
Өткізгіштік сименспен өлшенеді, (См) .
Электр қуаты P деп оң зарядтың орын ауыстыруынан болатын жұмыстың осы жұмысқа кеткен уақытқа қатынасын айтады:
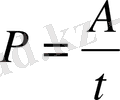
Электр қуаты ваттпен өлшенеді (Вт) .
Электр қуатының мəні кернеуді тоққа көбейткенге тең:
P = U · I .
1. 2 Тұрақты тоқ электр тізбектерінің заңдары
Ом заңы.
Тізбек бөлігі үшін Ом заңы (1. 3-сурет) . Тізбек бөлігіндегі “1-2” тоқ, сол бөліктегі кернеуге тура, ал кедергісіне кері пропорционал:
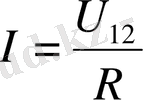
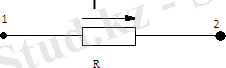
- - сурет
Құрамында ЭҚК бар тізбек бөліктері үшін Ом заңы. ЭҚК бар тізбек бөліктері үшін тоқ келесі формула бойынша анықталады:
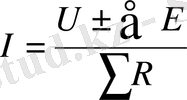
Егер тоқ пен ЭҚК бір бағытта болса “+” таңбамен, қарсы бағытта
болса “-“ таңбамен белгіленеді.
Мысалы, электр тізбегінің бір бөлігін қарастырайық (1. 4 - сурет)
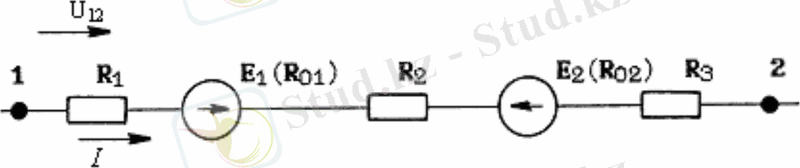
1. 4-сурет
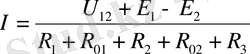
Кирхгофтың бірінші заңы. Электр тізбегінің кез келген түйінінде
тоқтардың алгебралық қосындысы нөлге тең:
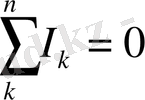
Кирхгофтың екінші заңы. Электр тізбегінің кез келген контурындағы ЭҚК-нің алгебралық қосындысы сол тізбекке кіретін кедергілерде кернеудің түсуінің алгебралық қосындысына тең:
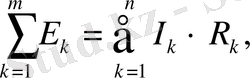
контурды айналу бағытымен тоқ пен ЭҚК-тің бағыты бағыттас болса,
“+” таңбамен жазылады.
Контурды айналу бағыты сағат тілімен бір бағытта немесе қарсы болып еркін алынады.
Жазу үлгісі: контур берілген делік (1. 6-сурет) .
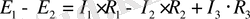
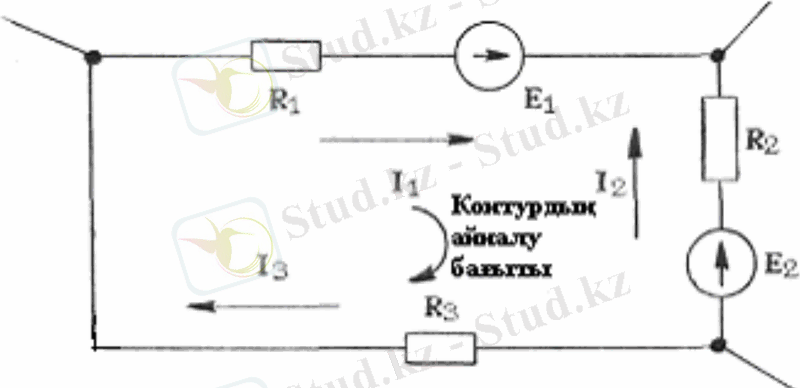
1. 6-сурет
2 Контурлық токтар әдісі
Күрделі электр тізбегінің режимін есептеу үшін, контурлық токтар әдісін пайдаланып, Кирхгофтың екінші заңына құрылған n
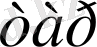 - (n
- (n
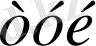 - 1) - N
- 1) - N
 тәуелсіз теңдеулерді бірлестіріп шешумен ғана шектелуге болады, мұндай жағдайда да Кирхгофтың бірінші заңы әр уақытта орындалады. Сұлбада ток көздері кездескен жағдайларда тәуелсіз контурлық токтарды бір ғана ток көзі арқылы бағыттау ұсынылады. Әдетте, ток көзі белгілі деп саналады. Қалған
К
контурлық токтарын ток көзі жоқ тармақтар арқылы қабылдау керек.
тәуелсіз теңдеулерді бірлестіріп шешумен ғана шектелуге болады, мұндай жағдайда да Кирхгофтың бірінші заңы әр уақытта орындалады. Сұлбада ток көздері кездескен жағдайларда тәуелсіз контурлық токтарды бір ғана ток көзі арқылы бағыттау ұсынылады. Әдетте, ток көзі белгілі деп саналады. Қалған
К
контурлық токтарын ток көзі жоқ тармақтар арқылы қабылдау керек.
Тізбекті бұл әдіспен есептеу үшін контурлық ток пайдаланылады.
Контурлық ток - алынған контурдың әр бөлігі үшін бірдей болатын есептеу шамасы. Есептеуді мына ретпен жүргізеді:
а) тізбектің барлық тәуелсіз контурындағы контурлық токтардың бағытын бірдей етіп алады (сағат тілі бойынша немесе керісінше) ;
б) контурдың айналу бағытын да сондай бағытпен белгілейді.
Кирхгофтың екінші заңы бойынша, контурдың әрқайсысына тәуелсіз теңдеулер құрылады. Бұл үшін әрбір контурда кездесетін бөліктердегі ЭҚК-імен контурлық токтардың теңдеу құрылып жатқан контурға қатыстығын қарастырады.
в) алынған теңдеулер жүйесін шешіп, контурлық токтарды табады, ол арқылы тармақтардағы негізгі токтарды есептейді.
1. 12-суреттегі электр тізбектерін есептеу үшін, контурлық токтар әдісін пайдаланайық. Контурлық токтар және олардың айналым бағыттары сағат тілінің бағытымен алынған.
1-2-3-1-контур үшін
 (R
(R
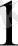 +R
+R
 ) -
) -
 R
R
 =E
=E
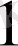 ;
;
1-3-6-1-контур үшін -
 R
R
 +
+
 ( R
( R
 +R
+R
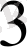 +R
+R
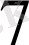 ) -
) -
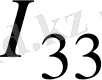 R
R
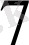 =E
=E
 ; (1. 32)
; (1. 32)
3-4-6-3-контур үшін -I
 R
R
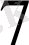 +
+
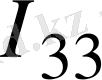 (R
(R
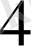 +R
+R
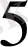 +R
+R
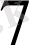 ) -
) -
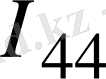 R
R
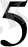 =-E
=-E
 ;
;
4-5-6-4-контур үшін -
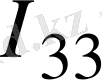 R
R
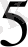 +
+
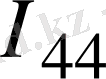 (R
(R
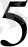 +R
+R
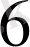 ) =-E
) =-E
 .
.
Берілген теңдеулер жүйесінен анықтағыштар арқылы немесе орын алмастыру тәсілімен (способ подстановки) контурлық токтарды табамыз.
Тармақтардағы негізгі токтарды табу үшін мынаны ескеру керек, егер кез келген тармақтан тек бір ғана контурлық ток өтсе, негізгі ток контурлық токтың өзіне тең, ал тармақтан бірнеше контурлық ток өтсе, онда негізгі ток осы контурлық токтардың алгебралық қосындысына тең. Сонымен 1. 12-сурет бойынша негізгі токтар мынаған тең:
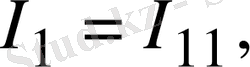
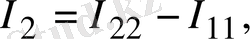
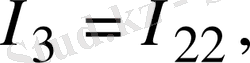
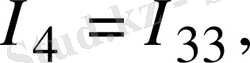
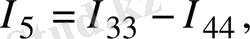
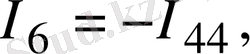
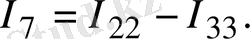 (1. 33)
(1. 33)
Берілген сұлбаны есептеу үшін, Кирхгоф заңдарымен жеті теңдеу (үшеуі І заң бойынша, ал төртеуі ІІ заң бойынша) жүйесін шешу қажет болар еді, ал контурлық токтар әдісі теңдеулер санын төртке дейін азайтуға мүмкіндік береді. Сондықтан теңдеулер Кирхгофтың екінші заңы бойынша құрылатын болғандықтан, бұл әдіс тізбекті есептеу және талдау үшін өте пайдалы (көбінесе тізбекте түйіндер саны тәуелсіз контурлар санынан көп болған уақытта) .
Контурлық токтар әдісінің кемшілігі есептеу дәлдігінің жеткіліксіздігіне, әсіресе негізгі токтарды бір-бірімен шамалас екі контурлық ток айырмасымен тапқанда.
2. 1 Контурлық токтардың матрица түрінде құрылған теңдеулері
Контурлық токтардың теңдеулерін матрица түрінде жазуға болады:
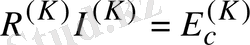 (1. 34)
(1. 34)
Мұндағы R
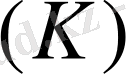 - контурлық кедергілерінің квадрат матрицасы;
- контурлық кедергілерінің квадрат матрицасы;
I
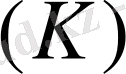 - контурлық токтардың тік жол матрицасы;
- контурлық токтардың тік жол матрицасы;
Е
 - контурдағы ЭҚК-терінің тік жол матрицасы.
- контурдағы ЭҚК-терінің тік жол матрицасы.
Есепке алынатын (1. 34) теңдеудегі ЭҚК көздерін және ток көздерін
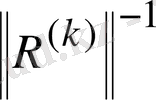 көбейтсек,
көбейтсек,
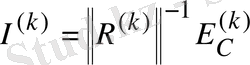 шығады. (1. 35)
шығады. (1. 35)
R
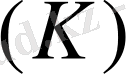 - контурлық кедергілердің матрицасын тікелей сұлбадан контурлық кедергілердің біріктіруші матрицасының В көмегімен алуға болатындығын көрсетейік:
- контурлық кедергілердің матрицасын тікелей сұлбадан контурлық кедергілердің біріктіруші матрицасының В көмегімен алуға болатындығын көрсетейік:
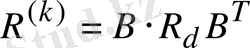 (1. 36)
(1. 36)
В - контурлық кедергілерінің біріктіруші матрицасы;
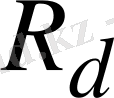 - тармақтардағы кедергілердің диагонал матрицасы;
- тармақтардағы кедергілердің диагонал матрицасы;
 - контурлық кедергілерінің транспонирленген біріктіруші матрицасы.
- контурлық кедергілерінің транспонирленген біріктіруші матрицасы.
Контурлық кедергілердің біріктіруші В құрғанда, оның жазық жолы (строка) тәуелсіз контур сандарына сайма-сай, ал тік жолдары тармақтар санына сай келеді. Матрицаның жазық және тік жолдарының қиылысында
 немесе 0 жазылады. Оның себебі берілген тармақтың тиісті контурға кіруіне немесе кірмеуіне байланысты. Егер контурдың айналу бағыты тармақтағы токтың бағытымен бағыттас болса, +1 оң таңбамен алынады, ал бағыттас болмаса, -1 теріс таңбамен алынады. Егер мұндағы тармақ тиісті контурға кірмесе, онда нөл жазылады, тармақ бағыты сол тармақтағы ток бағытымен бірдей деп алынса, контурлық ток бағыты контурдың айналу бағытымен бірдей деп алынады. Тәуелсіз контур құру үшін сұлбаның граф бағанасын (дерево графа) қабылдап алу керек, сонымен қатар байланыс тармағын анықтайды, демек контурлық токтар анықталады.
немесе 0 жазылады. Оның себебі берілген тармақтың тиісті контурға кіруіне немесе кірмеуіне байланысты. Егер контурдың айналу бағыты тармақтағы токтың бағытымен бағыттас болса, +1 оң таңбамен алынады, ал бағыттас болмаса, -1 теріс таңбамен алынады. Егер мұндағы тармақ тиісті контурға кірмесе, онда нөл жазылады, тармақ бағыты сол тармақтағы ток бағытымен бірдей деп алынса, контурлық ток бағыты контурдың айналу бағытымен бірдей деп алынады. Тәуелсіз контур құру үшін сұлбаның граф бағанасын (дерево графа) қабылдап алу керек, сонымен қатар байланыс тармағын анықтайды, демек контурлық токтар анықталады.
Тізбек графы деп тармақтарда орналасқан элементтерді көрсетпей-ақ барлық түйіндері мен барлық тармақтары келтірілетін сызбаны айтамыз. Граф бағанасы деп құрамында барлық түйіндері бар, бірақ ешқандай да тұйық контур жасамайтын графты айтады.
Идеалды ЭҚК көзі, яғни кедергісі жоқ тармақ сұлба бағанасы құрамына кіреді, ал тармақтағы идеалды ток көзі тогы байланыс тармағы құрамына кіреді.
Осы айтқандарды 1. 12-суреттегі сұлба бойынша қарастыратын болсақ, контурлық токтары
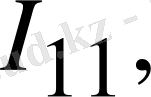

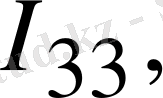 және
және
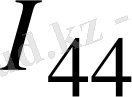 байланыс тармақтарындағы токтарға
байланыс тармақтарындағы токтарға
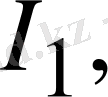
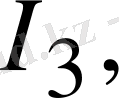
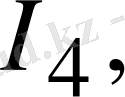 және
және
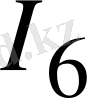 сайма-сай келеді.
сайма-сай келеді.
Граф бағанысы дегеніміз - ол сұлбадағы барлық түйіндерді жалғастыратын, бірақ бірде-бір тұйық контур құрмайтын тармақтар жиынтығы. Байланыстырушы тармақ дегеніміз - ол сұлба бағанасы құрамына кірмейтін кез келген тармақ. Ол тиісті бағаналарды толық сұлбаға дейін толықтырады. Бұдан былай «байланыс тармағы» терминін пайдаланамыз. Кез келген екі бағана түйіндерінің арасында бір ғана граф жолы кездеседі, ол - берілген екі түйін арасындағы үздіксіз тармақтар реттілігі, шарт бойынша әрбір түйін бір реттен артық кездеспеуге тиіс. Егер сұлба графы Y болса, онда бағана тармақтарының саны Y-1-ге тең болады, себебі Y тармақтардан әр уақытта контур құруға болады.
Контурлық кедергілердің біріктіруші матрицасы 7 тік жолдан және 4 жазық жолдан тұрады, яғни жазық жол тәуелсіз контурлар санына, ал тік жол тармақтар санына теңеседі:
В=


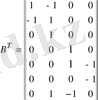
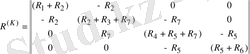
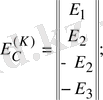
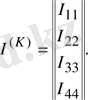
Тармақтардағы ток
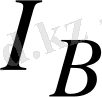 матрицасын контурлық ток матрицасы
матрицасын контурлық ток матрицасы
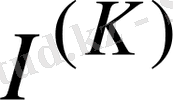 арқылы жеңіл табуға болады.
арқылы жеңіл табуға болады.
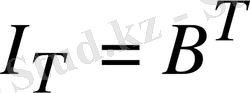
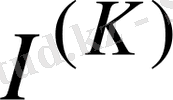 - осы теңдеуден тармақтардағы токтарды тура табамыз.
- осы теңдеуден тармақтардағы токтарды тура табамыз.
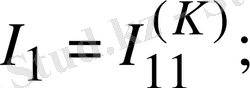
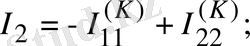
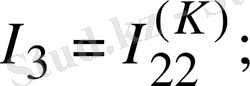
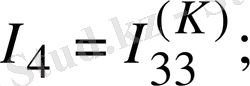
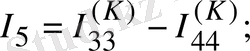
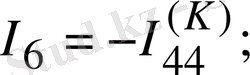
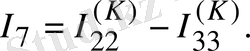
Егер сұлбада ЭҚК көзінен басқа, ток көзі де кездесетін болса, онда әрбір ток көзі тогы кез келген бағана тармағы бойынша тұйықталады деп қабылдауға болады және байланыс тармағы ток көзі тармағымен тұйық контур құрайды. Осы контурдағы әрбір кедергідегі ток көзі тогы әсерінен пайда болған кернеулердің түсуі Кирхгофтың екінші заңына құрылған теңдеудің сол жағына жазылады. Дегенмен осы кернеулерді кері таңбамен теңдеудің оң жағына шығаруға болатындығымен санасу керек. Теңдеуді 1. 13-суреттегі сұлбаға құруға болады:
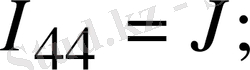
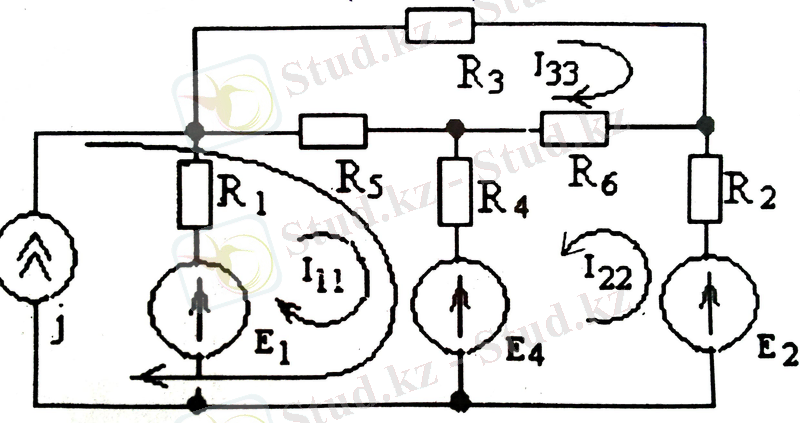
1. 13-сурет. Күрделі тармақтарған сұлба
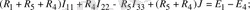

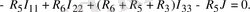
Осы құрылған теңдеулер қарастырылып отырған жағдайда ток J, R
 және R
және R
 кедергілері бар тармақтар арқылы ток көзі мен тұйық контур құрады.
кедергілері бар тармақтар арқылы ток көзі мен тұйық контур құрады.
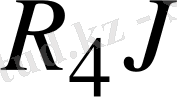 және
және
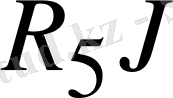 құрастырушы кернеулерін
құрастырушы кернеулерін
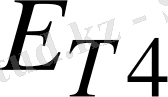 және
және
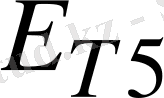 арқылы белгілеп, теңдеудің оң жағына шығарып жазады. Теңдеу жүйесін шешіп, контурлық токтарды табамыз, содан кейін тармақтардағы токтарды анықтаймыз.
арқылы белгілеп, теңдеудің оң жағына шығарып жазады. Теңдеу жүйесін шешіп, контурлық токтарды табамыз, содан кейін тармақтардағы токтарды анықтаймыз.
2. 2 Беттестіру принципі
Электр тізбектерін беттестіру принципіне сүйене отырып есептеуге болады. Бұл әдісті былай түсіндіреміз. Егер сызықты электр тізбектерінде бірнеше электр энергиясы көздерінің ЭҚК-тері берілген болса, онда тармақтағы ток әрбір ЭҚК-нің осы тізбекке әсер еткендегі пайда болған токтардың алгебралық қосындысына тең болады.
Есептеуді мына ретпен жүргіземіз:
а) кезекпе-кезек тізбек ішінде тек бір-бірден ғана энергия көзін қалдырып, ал басқа электр көздерін тізбектен алып тастап, олардың тек ішкі кедергілерін ғана r 10, r 20 қалдырады. Сонымен 1. 15а, б-суреттегідей әр энергия көзіне арналған есептеу сұлбасын алады.
б) біртіндеп түрлендіре отырып, есептеу сұлбасындағы тізбектің толық кедергісін табамыз және Ом заңын пайдаланып, әр тармақтағы токтарды есептейміз немесе белгілі әдістерінің біреуін пайдаланамыз.
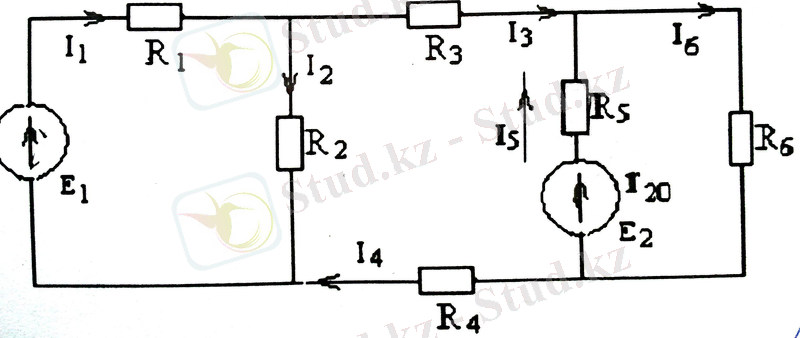
1. 14-сурет. Тармақталған электр тізбегі
в) тармақтағы токты табу үшін, беттестіру әдісі арқылы есептеу сұлбасындағы токтардың бағытын еске ала отырып, олардың алгебралық қосындысын табамыз. Ал бұл токтың бағытын ЭҚК-і бағыты арқылы оңай табуға болады.
1. 15а, б-суреттен мынаны жазуға болады:
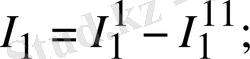
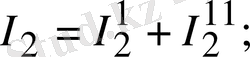
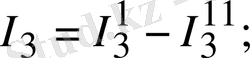
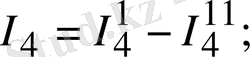
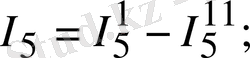
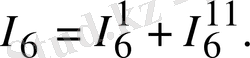
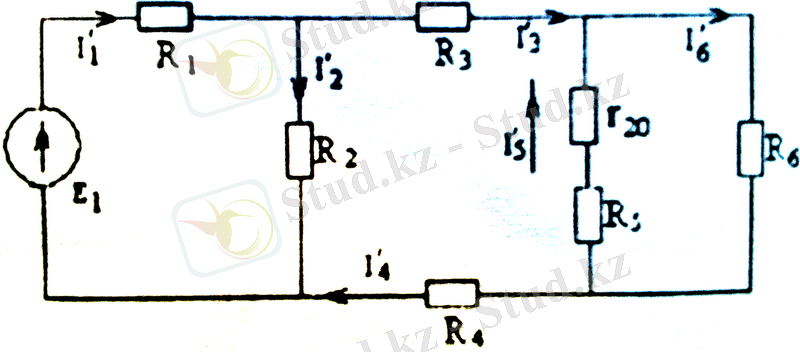
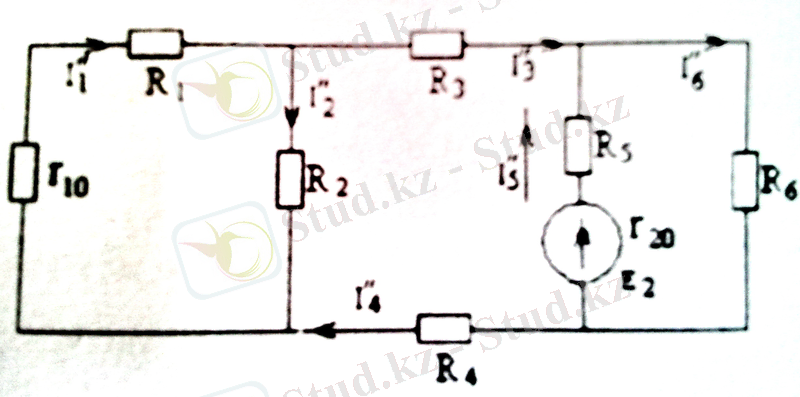
1. 15-сурет. Тармақталған электр сұлбалары
Беттестіру әдісімен есептеу кезінде кедергіде бөлініп шығатын қуатты құраушы токтардың қуаттарының қосындысымен есептеуге болмайды. Себебі, қуат дегеніміз - токтың екінші дәрежелі функциясы, яғни
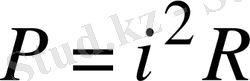 . Мұны түсіндіру үшін бір мысал қарастырайық. Қандай да бір кедергіден бір бағытта екі құраушы ток
. Мұны түсіндіру үшін бір мысал қарастырайық. Қандай да бір кедергіден бір бағытта екі құраушы ток
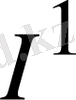 және
және
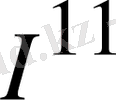 өтетін болса, онда осы кедергіде бөлініп шығатын қуат мынаған тең болар еді:
өтетін болса, онда осы кедергіде бөлініп шығатын қуат мынаған тең болар еді:
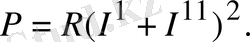
Ал бұл қуат құраушы токтар арқылы бөлініп шыққан қуаттардың қосындысына тең емес:
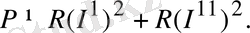
Беттестіру принциптері сызықты теңдеулердің жалпы қасиеттері салдарынан шығады, сондықтан бір-бірімен сызықты тәуелділікте болатын кез келген физикалық шамаларға пайдалануға болады.
Электр тізбектерінде берілген ЭҚК-і және кедергі арқылы тек токты ғана тауып қоймай, берілген кедергімен табылған ток арқылы кернеуді табуға болады.
Беттестіру әдісінің құндылығы - ол теңдеулер жүйесін шешуді қажет етпейді, ал оның кемшілігі есептеу дәлдігінің жеткіліксіздігінде, әсіресе тармақтағы токты шамалас келген құраушы токтардың айырмасымен тапқанда.
Көбінесе бұл әдіс тізбектегі энергия көздері санаулы ғана болған кезде тиімді. Кей кезде тізбектегі ЭҚК-і өзгеріп, бірнеше мәнге ие болғанда, мұндай тізбектің жұмысына талдау жасағанда есептеу нәтижелілігі ұлғаяды.
2. 3 Түйіндік әлеуеттер әдісі
Кез келген тізбектің режимі Кирхгофтың заңдарына байланысты құрылған теңдеулер арқылы өрнектеледі. Барлық «m» тармақтағы токты анықтау үшін, белгісіздері бар «m» теңдеулер жүйесін шешу керек. Ал түйіндік әлеуеттер әдісін қолдана отырып, теңдеулер санын қысқартуға болады.
Егер Ом заңын пайдаланғыңыз келсе, онда түйіндік әлеуеттерді білуіңіз керек. Мысалы, сұлбада
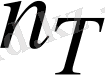 түйін болсын делік. Ойша сұлбаның бір түйінін жерге жалғасақ, тармақтағы токтардың таралуы өзгеріссіз қалады. Яғни сол түйіннің әлеуетін нөлге тең деп аламыз. Бұл жағдайда белгісіздер саны
түйін болсын делік. Ойша сұлбаның бір түйінін жерге жалғасақ, тармақтағы токтардың таралуы өзгеріссіз қалады. Яғни сол түйіннің әлеуетін нөлге тең деп аламыз. Бұл жағдайда белгісіздер саны
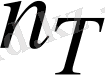 -дан
-дан
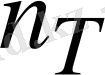 -1-ге дейін кемиді.
-1-ге дейін кемиді.
1. 16-суреттегі мысалдарды қарастырайық: үшінші түйіннің әлеуетін нөл деп аламыз немесе
 Бұл есептің шартын өзгертпейді. Себебі, әрбір тармақтағы ток әлеуеттердің абсолюттік мәніне емес, тармақтағы әлеуеттер айырымына байланысты болады.
Бұл есептің шартын өзгертпейді. Себебі, әрбір тармақтағы ток әлеуеттердің абсолюттік мәніне емес, тармақтағы әлеуеттер айырымына байланысты болады.
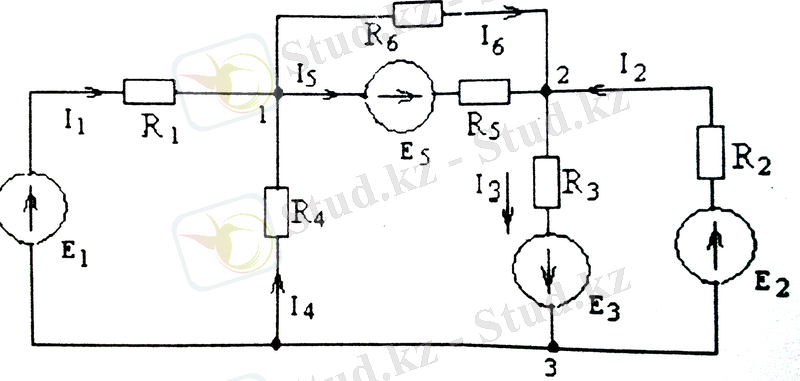
1. 16-сурет. Тармақталған электр сұлбасы
Сұлбада ток бағыттарын қалауымызша қабылдаймыз. Келісім бойынша түйннен шығатын токты оң таңбамен, түйінге кіретін токты теріс таңбамен аламыз. Қабылдап алған токтардың бағыты мен сұлбаның бірінші және екінші түйіндері үшін Кирхгофтың бірінші заңына жазылған теңдеулер құрамыз:
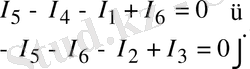 (1. 37)
(1. 37)
Ом заңына жазылған тармақтардағы токтар:
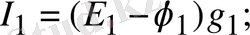
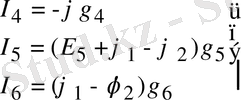 (1. 38)
(1. 38)
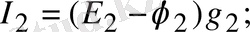
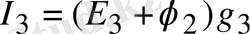
 және
және
 бірінші және екінші түйіндерінің әлеуеттері
бірінші және екінші түйіндерінің әлеуеттері
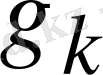 тармақтың өткізгіштігі
тармақтың өткізгіштігі
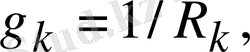 k
- бүтін сан.
k
- бүтін сан.
(1. 38) теңдеудегі токтардың мәні (1. 37) теңдеуге қойып, ұқсас мүшелерін біріктіруіміз керек:

 . (1. 39)
. (1. 39)
немесе
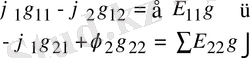
Мұндағы
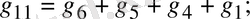
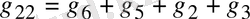 бірінші және екінші түйіндерге қосылған тармақтардың өткізгіштігінің қосындысын меншікті деп атайды.
бірінші және екінші түйіндерге қосылған тармақтардың өткізгіштігінің қосындысын меншікті деп атайды.
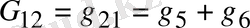 - осы түйіндерді бір-бірімен байланыстыратын тармақтардағы өткізгіштердің қосындысын жалпы өткізгіштік деп атайды. (1. 39) теңдеудің оң жағында
- осы түйіндерді бір-бірімен байланыстыратын тармақтардағы өткізгіштердің қосындысын жалпы өткізгіштік деп атайды. (1. 39) теңдеудің оң жағында
 тармақтағы ЭҚК-і мен оның өткізгіштердің көбейтінділерінің алгебралық қосындылары көрсетілген. Олардың сол қарастырылып отырған түйінге келіп қосылған тармақтарға ғана қатысты екенін айту қажет.
тармақтағы ЭҚК-і мен оның өткізгіштердің көбейтінділерінің алгебралық қосындылары көрсетілген. Олардың сол қарастырылып отырған түйінге келіп қосылған тармақтарға ғана қатысты екенін айту қажет.
ЭҚК-і қарастырлып отырған түйінге қарай бағытталса, Еg көбейтіндісі оң таңбамен алынады, ал егер ЭҚК-і қарастырылып отырған түйіннен тыс бағытталса, теріс таңбамен алынады. (1. 39) теңдеу алынған тармақтағы токтың бағытына байланысты болмайды. Қарастырылып отырған түйін дегеніміз - ол меншікті өткізгіштігі бар түйіндер
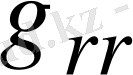 . Егер электр сұлбасы тек қана энергия көзінің ЭҚК-нен ғана емес, ток көзінен де тұратын болса, онда Кирхгофтың бірінші заңына байланысты алынған теңдеулер құрамына ток көзінің токтары да кіреді.
. Егер электр сұлбасы тек қана энергия көзінің ЭҚК-нен ғана емес, ток көзінен де тұратын болса, онда Кирхгофтың бірінші заңына байланысты алынған теңдеулер құрамына ток көзінің токтары да кіреді.
(1. 39) теңдеуді құру кезінде берілген ток көзінің токтары әр түйін үшін теңдеудің оң жағындағы қосылғыштары болып табылады. Бұл жағдайда да ток көзінің бағыты қарастырылып отырған түйінге бағытталса, оң, ал керісінше бағытталса теріс алынады. Мысалға 1. 17-суреттегі нөлге теңейміз.
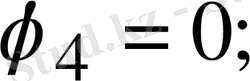 1, 2 және 3 түйіндер үшін теңдеулер құрамыз:
1, 2 және 3 түйіндер үшін теңдеулер құрамыз:
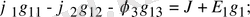
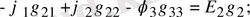
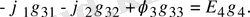
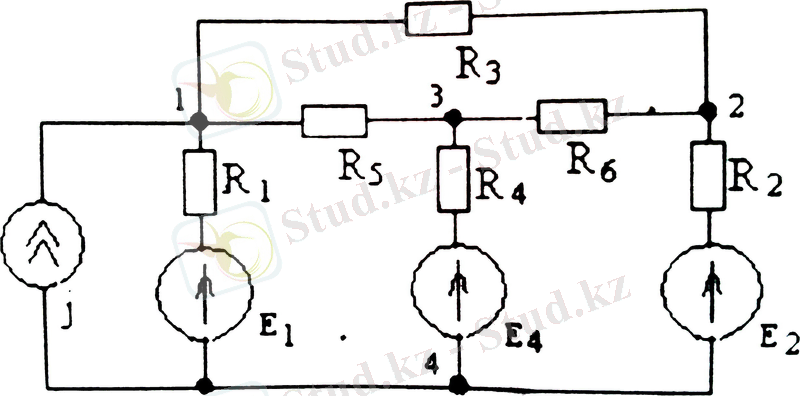
1. 17-сурет. Тармақталған электр сұлбасы
Мұндағы
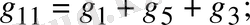
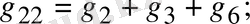
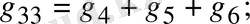
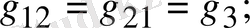
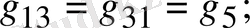
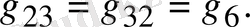
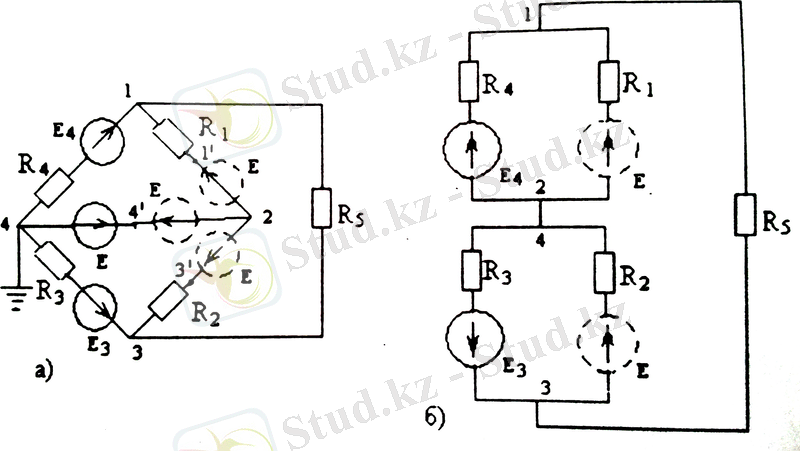
1. 18-сурет. Тармақталған электр сұлбасы
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz