Мектеп математикасында функция ұғымы, шегі және туындысы: берілу тәсілдері, қасиеттері және зерттеу әдістері


Жоспар:
Кіріспе.
І бөлім. Функция ұғымы.
1. 1. Функция ұғымы, функцияның берілу тәсілдері.
1. 2. Функциялардың негізгі қасиеттері.
1. 3. Негізгі элементар функциялар.
ІІ бөлім. Функцияның нүктедегі шегі.
2. 1. Функцияның нүктедегі шегін есептеудің әдістері.
2. 2. Функцияның шегін есептеуге қажетті формулалар.
ІІІ бөлім. Функцияның туындысы. Функцияны бірінші және екінші ретті туындылар арқылы зерттеу.
3. 1. Өспелі, кемімелі, кемімейтін, өспейтін және тұрақты болып келетін функциялардың белгілері.
3. 2. Функцияның экстремумы.
3. 3. Функцияның графигін оның мінездік нүктелері арқылы салу.
Қорытынды.
Қолданылған әдебиет.
К І Р І С П Е
Мектеп математикасы курсындағы функция ұғымы негізгі ұғымдардың біріне жатады. Функциялық тәуелділік өмірдегі өзгерісті нақты және толық түрде кескіндеуге мүмкіндік береді, ол шамалар арасындағы өзара байланысты түсініп анықтауға үлкен септігін тигізеді.
Функция ұғымы тек математикада ғана емес, басқа оқу пәндерінде де кеңінен пайдаланылады. Өйткені, табиғат құбылыстары арасындағы байланыстар математикалық түрде өрнектелгенде, яғни қарастырылып отырған шамалар арасында функциялық тәуелділік берілгенде ғана, тек сонда ғана нақты заңдылық түрінде тұжырымдама алатындығы белгілі. Сондықтан, мектеп оқушыларының функция ұғымын дұрыс меңгеруіне көп көңіл бөлінуі керек. Функция ұғымының ғылымға енуі Р. Декарттың “айнымалы шама” ұғымымен тығыз байланысты. “Функция” ұғымын ғылымға (XVII ғ-ң аяғында) Г. Лейбниц енгізді. Ол латынның “функтус” деген сөзінен шығып, қазақ тілінде “атқару” деген мағынаны білдіреді.
Табиғат құбылыстарын зерттеу жаратылыстану ғылымдарында кездесетін шамалар ұғымдарына алып келеді. Табиғат құбылыстарын байқау, тәжірибелер арқылы білу, физикалық, химиялық, биологиялық т. б. ғылымдарда кездесетін шамалардың өзара байланыста болатындығын көрсетеді. Мысалы:
1. Өткізгіштің бойымен электр тогы жүргенде, өткізгіш температурасы өзгеріп, жылу пайда болады. Электр тогының күші, өткізгіш кедергісі, уақыт және жылу мөлшерінің арасындағы тәуелділікті байқаймыз. Бұл мысалда электр тогының күші, өткізгіш кедергісі және уақыттың белгілі бір мәніне жылу мөлшерінің бір мәні сәйкес келеді.
2. Белгілі бір биіктіктен өз еркімен түсіп келе жатқан дененің қозғалысын байқап, уақыт пен дененің жүрген жолы ұзындығының арасындағы өзара байланысқа назар аударалық. Мұнда уақыттың әрбір мезетіне жолдың бір тиянақты ұзындығы сәйкес келеді.
Осындай мысалдарды көптеп келтіруге болады.
Анықтама. Егер бір белгілі ереже немесе заңдылық бойынша
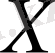 жиынындағы
жиынындағы
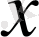 -ң әрбір мәніне
-ң әрбір мәніне
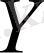 жиынының тиянақты бір
жиынының тиянақты бір
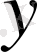 мәні сәйкес келсе, онда
мәні сәйкес келсе, онда
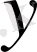 -ті
-ті
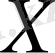 жиынында анықталған немесе берілген функция деп атайды және оны былай жазады:
жиынында анықталған немесе берілген функция деп атайды және оны былай жазады:
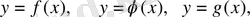 т. б. (1)
т. б. (1)
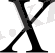 жиынында өзгеретін айнымалы
жиынында өзгеретін айнымалы
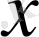 -ті тәуелсіз айнымалы немесе функцияның аргументі деп ататйды,
-ті тәуелсіз айнымалы немесе функцияның аргументі деп ататйды,
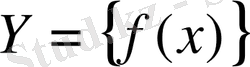 жиынында өзгеретін айнымалы
жиынында өзгеретін айнымалы
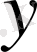 -ті тәуелді айнымалы немесе функция деп атайды. Тәуелсіз айнымалы немесе аргумент
-ті тәуелді айнымалы немесе функция деп атайды. Тәуелсіз айнымалы немесе аргумент
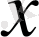 өзгеретін
өзгеретін
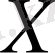 жиынын функцияның анықталу облысы деп атайды, ал тәуелді айнымалы немесе функция
жиынын функцияның анықталу облысы деп атайды, ал тәуелді айнымалы немесе функция
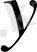 өзгеретін
өзгеретін
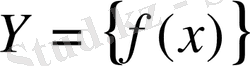 жиыны функция мәндерінің облысы деп аталады. Сонымен, функция, аргумент ұғымдары - өзімізді қоршап тұрған табиғаттың құбылыстарын зерттеудің нәтижесінде пайда болған ұғымдар.
жиыны функция мәндерінің облысы деп аталады. Сонымен, функция, аргумент ұғымдары - өзімізді қоршап тұрған табиғаттың құбылыстарын зерттеудің нәтижесінде пайда болған ұғымдар.
І Бөлім
1. 1. Функцияның берілу тәсілдері және оның негізгі қасиеттері.
Функциялар әр түрлі тәсілдер арқылы берілуі мүмкін. Біз функциялардың кестелік, графиктік және аналитикалқ тәсілдермен берілуіне тоқталамыз.
1. Функцияның кестелік тәсілмен берілуі. Функция кестелік тәсілмен берілген жағдайда алдымен аргумент мәндері алынады да, сонан кейін әр аргументке сәйкес келетін функция мәндері анықталып, кесте құрылады.
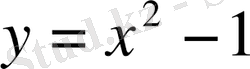 функциясы үшін кесте құрамыз:
функциясы үшін кесте құрамыз:
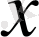
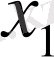
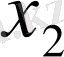
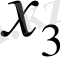
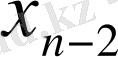
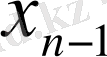
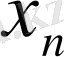
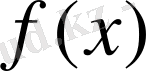
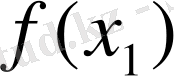
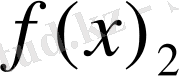
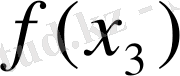
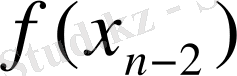
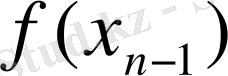
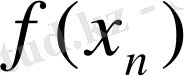
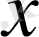
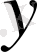
Берілген аргументтердің мәндері бойынша функцияның мәндерін анықтау біздерге қиын есеп емес. Алгебра курсынан белгілі:
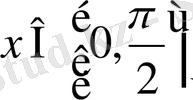 жағдайы үшін
жағдайы үшін
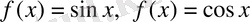 функцияларының мәндері кесте арқылы анықталған,
функцияларының мәндері кесте арқылы анықталған,
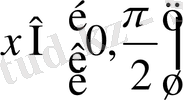 аралығында өзгергенде
аралығында өзгергенде
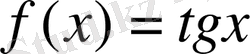 функциясының мәндері, ал
функциясының мәндері, ал
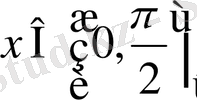 үшін
үшін
 функциясының мәндері кесте арқылы анықталған. Логарифмдік функцияның кестесі де функцияның кестелік тәсілмен берілуінің мысалы бола алады.
функциясының мәндері кесте арқылы анықталған. Логарифмдік функцияның кестесі де функцияның кестелік тәсілмен берілуінің мысалы бола алады.
2. Функцияның графиктік әдіспен берілуі.
Анықтама.
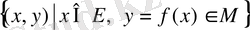 қос сандар жиынын
қос сандар жиынын
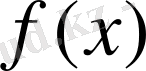 функциясының графигі деп атайды. Функцияның графигін координаттық жазықтыққа салады. Өзара перпендикуляр екі координаттық түзу және оларға ортақ
функциясының графигі деп атайды. Функцияның графигін координаттық жазықтыққа салады. Өзара перпендикуляр екі координаттық түзу және оларға ортақ
 координаттар басы орналасқан жазықтықты координаттар жазықтығы дейді. Горизонталь орналасқан түзуді абсциссалар осі деп атайды да,
координаттар басы орналасқан жазықтықты координаттар жазықтығы дейді. Горизонталь орналасқан түзуді абсциссалар осі деп атайды да,
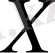 -пен белгілейді, вертикаль орналасқан түзуді ординаталар осі деп атап,
-пен белгілейді, вертикаль орналасқан түзуді ординаталар осі деп атап,
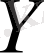 арқылы белгілейді, ал олардың қиылысу нүктесін координаттар басы дейді, оны
арқылы белгілейді, ал олардың қиылысу нүктесін координаттар басы дейді, оны
 әрпімен белгілейді. Тәуелсіз айнымалы
әрпімен белгілейді. Тәуелсіз айнымалы
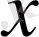 -ң мәндері абсциссалар осіне салынады. Ал
-ң мәндері абсциссалар осіне салынады. Ал
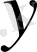 -ң мәндері ординаталар осінің бойына салынады.
-ң мәндері ординаталар осінің бойына салынады.
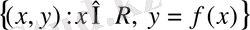 нүктелер жиыны берілсін.
нүктелер жиыны берілсін.
 осіне параллель түзулердің кез келгені осы нүктелер жиынын бір ғана нүктеде қиып өтетін болса, онда бұл нүктелер жиыны бір мәнді
осіне параллель түзулердің кез келгені осы нүктелер жиынын бір ғана нүктеде қиып өтетін болса, онда бұл нүктелер жиыны бір мәнді
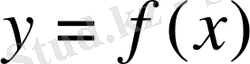 функциясын анықтайды (1-сурет) .
функциясын анықтайды (1-сурет) .
1-СУРЕТ
Сонымен, абсциссалары - тәуелсіз айнымалы, ал ординаталары - функция мәндері болып келген
 жазықтығындағы
жазықтығындағы
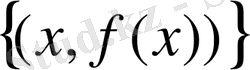 нүктелер жиынын
нүктелер жиынын
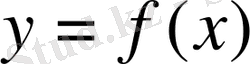 функциясының графигі деп атайды.
функциясының графигі деп атайды.
Бір мәнді
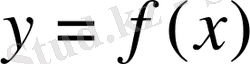 функциясының графигі
функциясының графигі
 жазықтығында орналасқан (функцияның анықталу облысына байланысты) біртұтас қисық. Анықталу облысының ішінде
жазықтығында орналасқан (функцияның анықталу облысына байланысты) біртұтас қисық. Анықталу облысының ішінде
 осіне параллель жүргізілген түзулер қисықпен бір ғана нүктеде қиылысады (2-сурет) .
осіне параллель жүргізілген түзулер қисықпен бір ғана нүктеде қиылысады (2-сурет) .
2-СУРЕТ
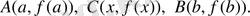
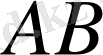 қисығы -
қисығы -
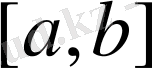 анықталу облысы болатын функцияның геометриялық кескіні.
анықталу облысы болатын функцияның геометриялық кескіні.
3. Функцияның аналитикалық тәсілмен берілуі. Айнымалылар арасындағы сәйкестік формуламен берілсе, онда функция аналитикалық түрде берілді дейді. Төменде берілген функциялар аналитикалық тәсілге мысал бола алады:
1) Тура пропорционалдық тәуелділік -
 , мұнда
, мұнда
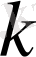 - тұрақты,
- тұрақты,
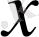 - тәуелсіз айнымалы,
- тәуелсіз айнымалы,
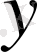 - тәуелді айнымалы.
- тәуелді айнымалы.
2) Кері пропорционалдық тәуелділік -
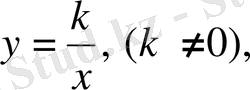 мұнда
мұнда
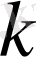 - тұрақты,
- тұрақты,
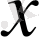 - тәуелсіз айнымалы,
- тәуелсіз айнымалы,
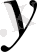 - тәуелді айнымалы.
- тәуелді айнымалы.
3) Сызықтық функция -
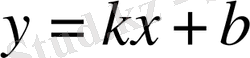 , мұнда
, мұнда
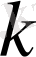 және
және
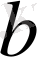 - тұрақты сандар,
- тұрақты сандар,
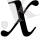 - тәуелсіз айнымалы,
- тәуелсіз айнымалы,
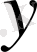 - тәуелді айнымалы.
- тәуелді айнымалы.
4) Көрсеткіштік функция -
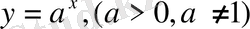 , мұнда
, мұнда
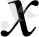 - тәуелсіз айнымалы,
- тәуелсіз айнымалы,
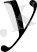 - тәуелді айнымалы.
- тәуелді айнымалы.
5) Логарифмдік функция -
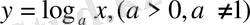 , мұнда
, мұнда
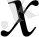 - тәуелсіз айнымалы,
- тәуелсіз айнымалы,
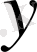 - тәуелді айнымалы.
- тәуелді айнымалы.
6) Дәрежелік функция -
 мұнда
мұнда
 - кез келген нақты сан,
- кез келген нақты сан,
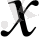 - тәуелсіз айнымалы,
- тәуелсіз айнымалы,
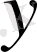 - тәуелді айнымалы.
- тәуелді айнымалы.
7) Тригонометриялық функциялар -
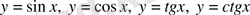 , мұнда
, мұнда
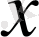 - тәуелсіз айнымалы,
- тәуелсіз айнымалы,
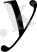 - тәуелді айнымалы.
- тәуелді айнымалы.
8) Кері тригонометриялық функциялар -
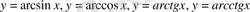 , мұнда
, мұнда
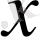 - тәуелсіз айнымалы,
- тәуелсіз айнымалы,
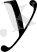 - тәуелді айнымалы.
- тәуелді айнымалы.
Міне, осы функциялардың барлығы - аналитикалық тәсілмен беріліп тұрған функциялар. Осы функциялардың көптеген қасиеттерін білеміз. Анықталу облыстарын және мәндерінің өзгеру облыстарын анықтай аламыз. Графиктерін құра аламыз.
Енді функциялардың негізгі қасиеттеріне тоқталайық.
1. 2. Жұп және тақ функциялар.
Егер
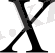 жиынында оның кез келген
жиынында оның кез келген
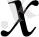 элементімен қатар
элементімен қатар
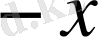 элементі де бар болса, онда бұл жиын симметриялы жиын деп аталады. Мысалы,
элементі де бар болса, онда бұл жиын симметриялы жиын деп аталады. Мысалы,
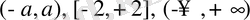 - симметриялы жиындар.
- симметриялы жиындар.
Анықтама. Егер
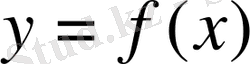 функциясының анықталу облысының кез келген
функциясының анықталу облысының кез келген
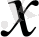 үшін
үшін
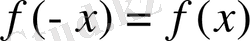 теңдігі орындалса, онда ол жұп функция деп аталады.
теңдігі орындалса, онда ол жұп функция деп аталады.
Анықтама. Егер
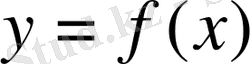 функциясының анықталу облысының кез келген
функциясының анықталу облысының кез келген
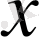 үшін
үшін
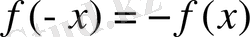 теңдігі орындалса, онда ол тақ функция деп аталады.
теңдігі орындалса, онда ол тақ функция деп аталады.
Мысалы,
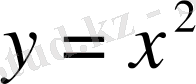 - жұп функция, себебі:
- жұп функция, себебі:
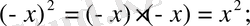
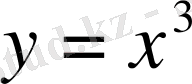 - тақ функция, себебі:
- тақ функция, себебі:
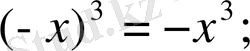 Ал
Ал
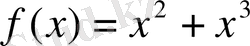 функциясы жұп функцияға да, тақ функцияға да жатпайды, себебі:
функциясы жұп функцияға да, тақ функцияға да жатпайды, себебі:
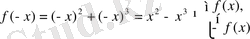
Жұп функцияның графигі ордината осіне қарағанда симметриялы қисық болады. Тақ функцияның графигі бас нүктеге қарағанда симметриялы қисық болады.
Мысалы: 1.
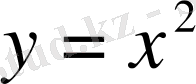 ; 2.
; 2.
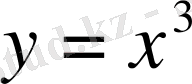 функцияларының графиктерін салайық.
функцияларының графиктерін салайық.
1.
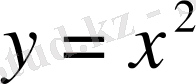 - жұп функция.
- жұп функция.
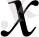
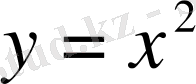
Енді осы нүктелерді координаталар жазықтығына түсірелік. Нүктелерді толқынды қисықпен қоссақ,
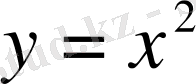 параболасы шығады (3-сурет) .
параболасы шығады (3-сурет) .
3-СУРЕТ
2.
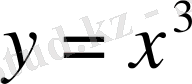 - тақ функция.
- тақ функция.
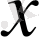
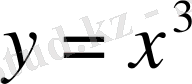
Осы нүктелерді координаттар жазықтығына түсіріп, оларды толқынды қисықпен қоссақ,
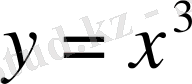 кубтық параболасы шығады (4-сурет) .
кубтық параболасы шығады (4-сурет) .
4-СУРЕТ
Тригонометриялық функциялардан
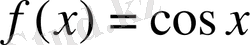 - жұп функция, ал
- жұп функция, ал
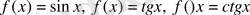 функциялары тақ функциялар болып табылады.
функциялары тақ функциялар болып табылады.
Мысалы: а)
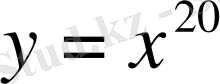 ; б)
; б)
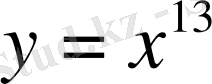 ; в)
; в)
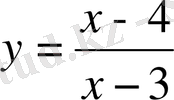 функцияларын жұп-тақтылыққа зерттеу керек.
функцияларын жұп-тақтылыққа зерттеу керек.
Шешуі: а)
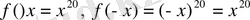 , олай болса,
, олай болса,
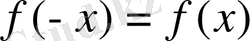 , барлық
, барлық
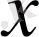 үшін функция жұп болады.
үшін функция жұп болады.
б)
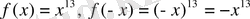 , олай болса,
, олай болса,
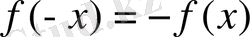 , барлық
, барлық
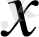 үшін функция тақ болады.
үшін функция тақ болады.
в)
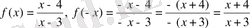 , яғни
, яғни
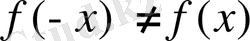 және
және
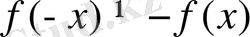 болғандықтан, функция жұп та, тақ та емес.
болғандықтан, функция жұп та, тақ та емес.
3. Бірсарынды функциялар.
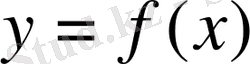 функциясын
функциясын
 аралығында қарастырайық.
аралығында қарастырайық.
Анықтама. Егер
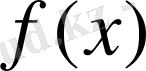 функциясының анықталу жиынындағы кез келген
функциясының анықталу жиынындағы кез келген
 сандары үшін
сандары үшін
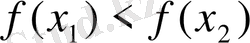 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
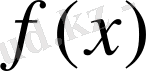 функциясы өспелі функция деп аталады.
функциясы өспелі функция деп аталады.
Анықтама. Егер
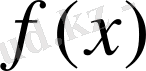 функциясының анықталу жиынындағы кез келген
функциясының анықталу жиынындағы кез келген
 сандары үшін
сандары үшін
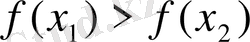 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
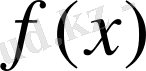 функциясы кемімелі функция деп аталады.
функциясы кемімелі функция деп аталады.
Анықтама. Егер
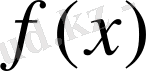 функциясының анықталу жиынындағы кез келген
функциясының анықталу жиынындағы кез келген
 сандары үшін
сандары үшін
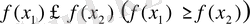 болса, онда
болса, онда
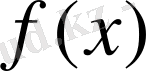 функциясын кемімейтін (өспейтін) функция деп атайды.
функциясын кемімейтін (өспейтін) функция деп атайды.
Мысалы,
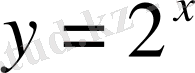 және
және
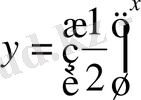 екі көрсеткіштік функцияларын алайық. Бірінші функцияның негізі
екі көрсеткіштік функцияларын алайық. Бірінші функцияның негізі
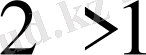 , сондықтан ол өспелі функция болады. Оны анықтама арқылы тексеріп көрсек болады.
, сондықтан ол өспелі функция болады. Оны анықтама арқылы тексеріп көрсек болады.
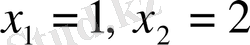 деп алайық,
деп алайық,
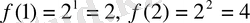 , яғни
, яғни
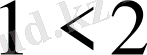 , ал
, ал
 . Өспелі функцияның анықтамасындағы теңсіздік орындалды. Екінші
. Өспелі функцияның анықтамасындағы теңсіздік орындалды. Екінші
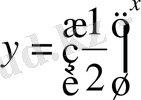 функциясының негізі
функциясының негізі
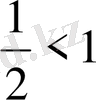 . Бұл жағдайда
. Бұл жағдайда
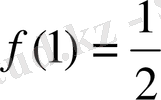 , ал
, ал
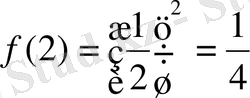 , сонда
, сонда
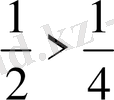 . Демек,
. Демек,
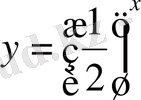 функциясы - кемімелі функция. Функциялардың графиктері төмендегідей болады (5-сурет) .
функциясы - кемімелі функция. Функциялардың графиктері төмендегідей болады (5-сурет) .
5-СУРЕТ
Өспелі және кемімелі функцияларды және өспейтін функцияларды бірсарынды функциялар деп атайды. Мысалы,
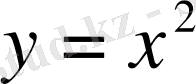 функциясына назар аударсақ,
функциясына назар аударсақ,
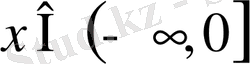 аралығында функция - кемімелі, ал
аралығында функция - кемімелі, ал
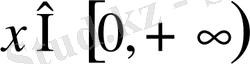 аралығында функция - өспелі.
аралығында функция - өспелі.
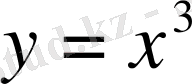 функциясы
функциясы
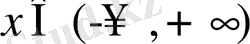 аралығында - өспелі функция.
аралығында - өспелі функция.
4. Периодты функциялар.
Егер
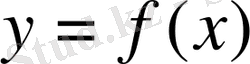 функциясының аргументі
функциясының аргументі
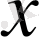 -ке
-ке
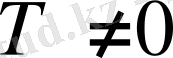 санын қосқаннан функцияның мәні өзгермесе, яғни
санын қосқаннан функцияның мәні өзгермесе, яғни
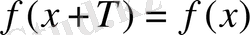 теңдігі орындалса, онда ол периодты функция деп аталады.
теңдігі орындалса, онда ол периодты функция деп аталады.
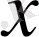 және
және
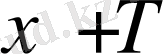 нүктелері - функцияның анықталу облысындағы нүктелер.
нүктелері - функцияның анықталу облысындағы нүктелер.
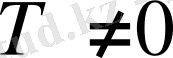 саны функцияның периоды деп аталады.
саны функцияның периоды деп аталады.
Мысалы: а)
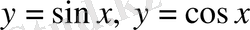 функциялары -
функциялары -
 периодты функциялар,
периодты функциялар,
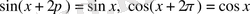 . Бұл функциялар үшін
. Бұл функциялар үшін
 - ең кіші периоды. Сонымен бірге, бұл функциялар -
- ең кіші периоды. Сонымен бірге, бұл функциялар -
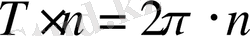 периодты функциялар, яғни
периодты функциялар, яғни
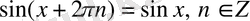 ,
,
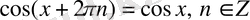 .
.
б)
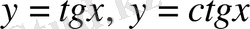 функциялары -
функциялары -
 периодты функциялар, яғни
периодты функциялар, яғни
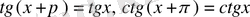 ,
,
 - бұл функциялардың ең кіші периоды. Сонымен бірге, бұл функциялар -
- бұл функциялардың ең кіші периоды. Сонымен бірге, бұл функциялар -
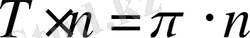 периодты функциялар, яғни
периодты функциялар, яғни
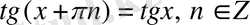 ,
,
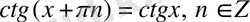 . Тригонометриялық функциялардың периодты функция болатындығын дәлелдеу қиын емес.
. Тригонометриялық функциялардың периодты функция болатындығын дәлелдеу қиын емес.
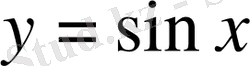 функциясының периодтылығын дәлелдейік, яғни
функциясының периодтылығын дәлелдейік, яғни
 болатынына көз жеткізейік. Ол үшін
болатынына көз жеткізейік. Ол үшін
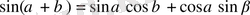 формуласын пайдаланамыз. Сонда
формуласын пайдаланамыз. Сонда
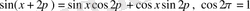 , ал
, ал
 екенін ескерсек,
екенін ескерсек,
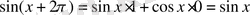 . Демек,
. Демек,
 .
.
1. 3. Негізгі элементар функциялар.
Элементар функцияларға дәрежелік, көрсеткіштік, логарифмдік, тригонометриялық және кері тригонометриялық функциялар жатады.
1. Дәрежелік функция.
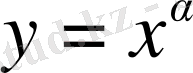 түріндегі функция осылай аталады, мұндағы
түріндегі функция осылай аталады, мұндағы
 - кез келген нақты сан, яғни
- кез келген нақты сан, яғни
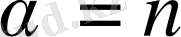 болғанда рационал функция
болғанда рационал функция
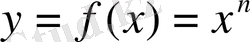 шығады және ол сан түрінде анықталады.
шығады және ол сан түрінде анықталады.
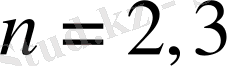 болғанда
болғанда
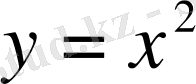 және
және
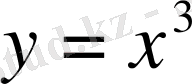 функциялары шығады. Бұлардың графиктерін тиісінше квадрат және кубтық парабола дейді.
функциялары шығады. Бұлардың графиктерін тиісінше квадрат және кубтық парабола дейді.
СУРЕТ
Осыған орай, кейде
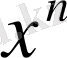 функциясының графигін
функциясының графигін
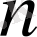 -ші дәрежелі парабола деп те атайды. Егер
-ші дәрежелі парабола деп те атайды. Егер
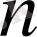 бүтін теріс сан болса, яғни
бүтін теріс сан болса, яғни
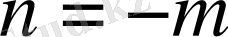 , онда
, онда
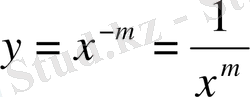 функциясын алар едік, ол координаттар жүйесінің бас нүктесінда анықталмайды, яғни
функциясын алар едік, ол координаттар жүйесінің бас нүктесінда анықталмайды, яғни
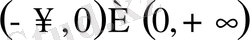 аралығында анықталады.
аралығында анықталады.
 болғанда
болғанда
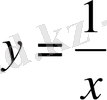 функциясы шығады және оның графигінің тең бүйірлі гипербола деген арнайы атауы бар. Егер
функциясы шығады және оның графигінің тең бүйірлі гипербола деген арнайы атауы бар. Егер
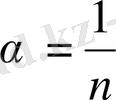 (мұндағы
(мұндағы
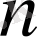 - оң бүтін сан) болса, онда
- оң бүтін сан) болса, онда
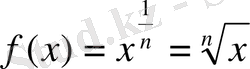 иррационал функция шығады. Қарастырған мысалдарға сүйеніп, дәрежелік функцияны
иррационал функция шығады. Қарастырған мысалдарға сүйеніп, дәрежелік функцияны
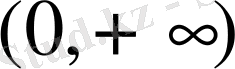 аралығында анықталады деп айтуымызға болады.
аралығында анықталады деп айтуымызға болады.
Көпмүшелер. Мынадай функция қарастырайық:
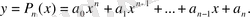
Көпмүше - дәрежелік функциялар мен тұрақты сандардың көбейтінділерінің қосындысы болғандықтан, ол бүкіл нақты сандар жиынында анықталған.
 болғанда біріші дәрежелі көпмүше аламыз:
болғанда біріші дәрежелі көпмүше аламыз:
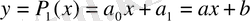 , мұны сызықтық функция деп атайды. Ол нақты сандар жиынында анықталған. Мысалы,
, мұны сызықтық функция деп атайды. Ол нақты сандар жиынында анықталған. Мысалы,
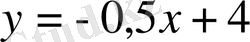 сызықтық функциясын қарастырайық. Шешуі: сызықтық функцияның графигі түзу болады. Ал түзуді салу үшін оның екі нүктесін білу жеткілікті. Кестені толтырайық.
сызықтық функциясын қарастырайық. Шешуі: сызықтық функцияның графигі түзу болады. Ал түзуді салу үшін оның екі нүктесін білу жеткілікті. Кестені толтырайық.
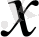
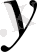
(
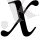 аргументіне 0 мен 4 мәндерін бердік те,
аргументіне 0 мен 4 мәндерін бердік те,
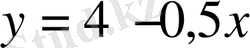 формуласы бойынша
формуласы бойынша
 -ң сәйкес мәнін таптық) Координаталық жазықтықта
-ң сәйкес мәнін таптық) Координаталық жазықтықта
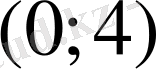 және
және
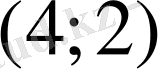 нүктелерін белгілейміз де, осы нүктелер арқылы түзу жүргіземіз. Сондай-ақ, функцияның абсцисса және ордината осьтерімен қиылысу нүктелерін табу үшін функцияның сәйкесінше нөлдерін анықтау қажет. Ордината осімен қиылысу нүктесін жоғарыда
нүктелерін белгілейміз де, осы нүктелер арқылы түзу жүргіземіз. Сондай-ақ, функцияның абсцисса және ордината осьтерімен қиылысу нүктелерін табу үшін функцияның сәйкесінше нөлдерін анықтау қажет. Ордината осімен қиылысу нүктесін жоғарыда
 деп алып,
деп алып,
 -ті таптық, ал абсцисса осімен қиылысу нүктесін табу үшін
-ті таптық, ал абсцисса осімен қиылысу нүктесін табу үшін
 теңдеуін шешу жеткілікті.
теңдеуін шешу жеткілікті.
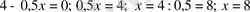 , яғни
, яғни
 нүктесінде
нүктесінде
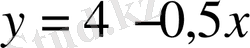 функциясының графигі абсцисса осін қиып өтеді.
функциясының графигі абсцисса осін қиып өтеді.
СУРЕТ
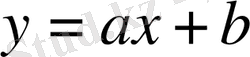 функциясының графигі
функциясының графигі
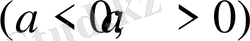 болған жағдайда мынадай болады (7-сурет) .
болған жағдайда мынадай болады (7-сурет) .
7-СУРЕТ
 болғанда
болғанда
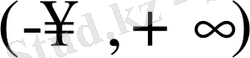 нақты сандар жиынында анықталған, графигі парабола болатын квадрат үшмүше аламыз:
нақты сандар жиынында анықталған, графигі парабола болатын квадрат үшмүше аламыз:
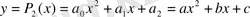 .
.
 болса, параболаның тармағы жоғары, ал
болса, параболаның тармағы жоғары, ал
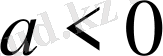 болғанда - төмен бағытталады (8, а, б, в-сурет) .
болғанда - төмен бағытталады (8, а, б, в-сурет) .
8-СУРЕТ
Бөлшек-рационал функция.
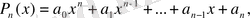
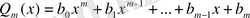 екі көпмүшенің қатынасы:
екі көпмүшенің қатынасы:
 бөлшек-рационал функция деп аталады. Ол бөлімдегі көпмүше нөлге айналмайтын
бөлшек-рационал функция деп аталады. Ол бөлімдегі көпмүше нөлге айналмайтын
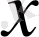 -ң мәндерінің жиынында анықталған.
-ң мәндерінің жиынында анықталған.
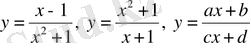 функциялары - бөлшек-рационал функциялар. Соңғысы бөлшек-сызықты функция деп аталады.
функциялары - бөлшек-рационал функциялар. Соңғысы бөлшек-сызықты функция деп аталады.
2. Көрсеткіштік функция.
Көрсеткіштік функцияның графигі.
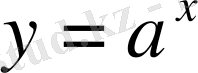 формуласымен берілген функцияны қарастырамыз. Мұнда
формуласымен берілген функцияны қарастырамыз. Мұнда
 - берілген сан,
- берілген сан,
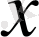 - белгісіз айнымалы.
- белгісіз айнымалы.
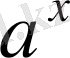 өрнегінің дәреже көрсеткіші
өрнегінің дәреже көрсеткіші
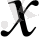 -ң кез келген мәнінде мағыналы болуы үшін дәреженің негізі
-ң кез келген мәнінде мағыналы болуы үшін дәреженің негізі
 оң сан болуы керек.
оң сан болуы керек.
 болғанда
болғанда
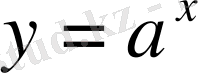 функциясы тұрақты болады, себебі
функциясы тұрақты болады, себебі
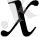 -ң кез келген мәнінде функция тек қана 1-ге тең мән қабылдайды. Сондықтан,
-ң кез келген мәнінде функция тек қана 1-ге тең мән қабылдайды. Сондықтан,
 болғанда функция қарастырылмайды.
болғанда функция қарастырылмайды.
Анықтама.
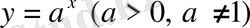 формуласымен берілген функция көрсеткіштік функция деп аталады.
формуласымен берілген функция көрсеткіштік функция деп аталады.
Мысалы,
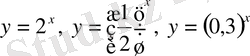 функциялары - көрсеткіштік функциялар,
функциялары - көрсеткіштік функциялар,
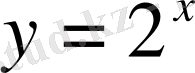 және
және
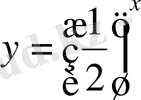 функцияларының графиктерін сызайық.
функцияларының графиктерін сызайық.
 және
және
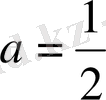 болғандағы
болғандағы
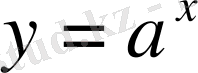 функциясына талдау жасайық.
функциясына талдау жасайық.
1)
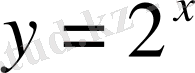 .
.
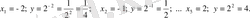
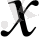
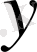
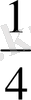
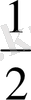
9-СУРЕТ
2)
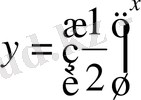 .
.
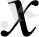
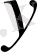
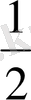
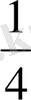
10-СУРЕТ
 үшін: 1) функцияның анықталу облысы - барлық нақты сандар жиыны:
үшін: 1) функцияның анықталу облысы - барлық нақты сандар жиыны:
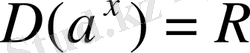 ; 2) функцияның мәндерінің жиыны:
; 2) функцияның мәндерінің жиыны:
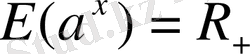 ; 3) бүкіл анықталу облысы бойында функция өседі, яғни
; 3) бүкіл анықталу облысы бойында функция өседі, яғни
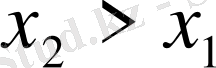 болғанда
болғанда
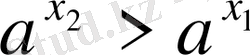 ; 4)
; 4)
 болғанда
болғанда
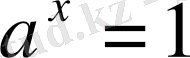 ;
;
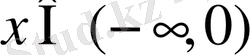 болғанда
болғанда
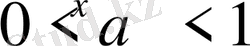 ;
;
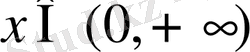 болғанда
болғанда
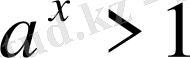 .
.
 үшін: 1) функцияның анықталу облысы - барлық нақты сандар жиыны:
үшін: 1) функцияның анықталу облысы - барлық нақты сандар жиыны:
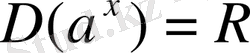 ; 2) функцияның мәндерінің жиыны:
; 2) функцияның мәндерінің жиыны:
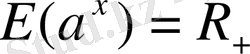 ; 3) бүкіл анықталу облысы бойында функция кемиді, яғни
; 3) бүкіл анықталу облысы бойында функция кемиді, яғни
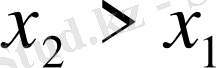 болғанда
болғанда
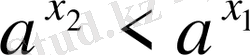 ; 4)
; 4)
 болғанда
болғанда
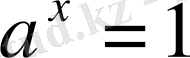 ;
;
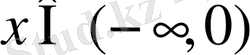 болғанда
болғанда
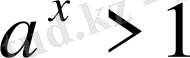 ; ;
; ;
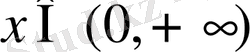 болғанда
болғанда
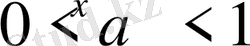 .
.
3. Логарифмдік функция.
Санның логарифмінің ұғымы.
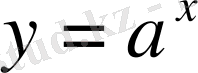 көрсеткіштік функция берілсін
көрсеткіштік функция берілсін
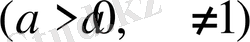 . Бұл - бірсарынды функция. Сондықтан аргументтің
. Бұл - бірсарынды функция. Сондықтан аргументтің
 әр мәніне функцияның бір ғана мәні сәйкес келіп қоймай, керісінше, функцияның алдын-ала берілген әр мәніне
әр мәніне функцияның бір ғана мәні сәйкес келіп қоймай, керісінше, функцияның алдын-ала берілген әр мәніне
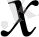 -ң бір ғана мәні сәйкес келеді.
-ң бір ғана мәні сәйкес келеді.
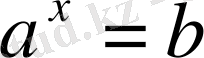 теңдеуін қарастырайық.
теңдеуін қарастырайық.
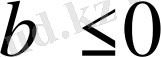 болғанда теңдеудің түбірі болмайды. Егер
болғанда теңдеудің түбірі болмайды. Егер
 болса, онда теңдеудің бір түбірі болады. Графикте көрсетейік.
болса, онда теңдеудің бір түбірі болады. Графикте көрсетейік.
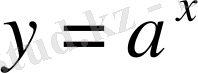 функциясының графигін сызамыз,
функциясының графигін сызамыз,
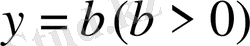 түзуін жүргіземіз. Осы екі графиктердің қиылысу нүктесінің абсциссасы, яғни
түзуін жүргіземіз. Осы екі графиктердің қиылысу нүктесінің абсциссасы, яғни
 -
-
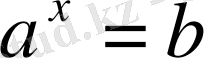 теңдеуінің іздеп отырған түбірі болады. Сонымен,
теңдеуінің іздеп отырған түбірі болады. Сонымен,
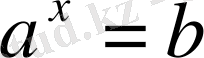
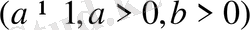 .
.
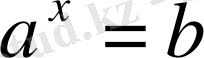 теңдеуінің түбірі
теңдеуінің түбірі
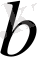 санының
санының
 негізді логарифмі деп аталады.
негізді логарифмі деп аталады.
Анықтама.
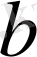 оң санының бірден өзгеше, оң
оң санының бірден өзгеше, оң
 негізді логарифмі деп,
негізді логарифмі деп,
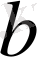 санын алу үшін
санын алу үшін
 санының дәреже көрсеткіші болатын
санының дәреже көрсеткіші болатын
 санын айтады:
санын айтады:
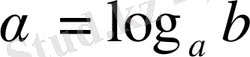 . Оқылуы: “
. Оқылуы: “
 дегеніміз
дегеніміз
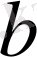 санының
санының
 негізді логарифмі”. Егер
негізді логарифмі”. Егер
 болса, онда былай жазылады:
болса, онда былай жазылады:
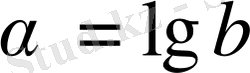 , яғни 10 саны негіз болып жазылмайды. Мұндай логарифмдер - ондық логарифмдер. Сонымен,
, яғни 10 саны негіз болып жазылмайды. Мұндай логарифмдер - ондық логарифмдер. Сонымен,
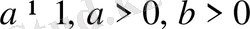 болғанда
болғанда
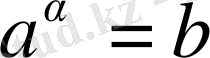 теңдеуінен анықтама бойынша
теңдеуінен анықтама бойынша
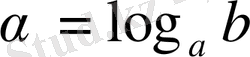 теңдігі шығады. Соңғы теңдеудегі
теңдігі шығады. Соңғы теңдеудегі
 -ң орнына мәнін қойсақ,
-ң орнына мәнін қойсақ,
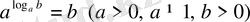 . Бұл теңдік негізгі логарифмдік теңбе-теңдік деп аталады. Мысалы,
. Бұл теңдік негізгі логарифмдік теңбе-теңдік деп аталады. Мысалы,
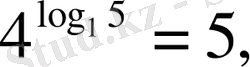
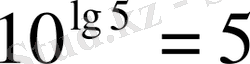 . Бір санының кез келген негізді логарифмі нөлге тең.
. Бір санының кез келген негізді логарифмі нөлге тең.
Логарифмдік функцияның графигі.
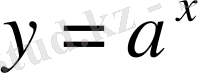 функциясы - бірсарынды. Демек, әрбір
функциясы - бірсарынды. Демек, әрбір
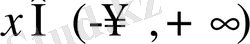 мәніне бір
мәніне бір
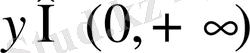 сәйкес келеді, керісінше, әрбір
сәйкес келеді, керісінше, әрбір
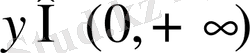 мәніне бір ғана
мәніне бір ғана
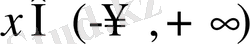 мәні сәйкес келеді, яғни
мәні сәйкес келеді, яғни
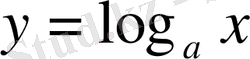 кері функциясы бар болады.
кері функциясы бар болады.
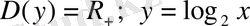 және
және
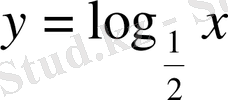 функцияларының графиктерін салайық (11-сурет) .
функцияларының графиктерін салайық (11-сурет) .
11-СУРЕТ
 және
және
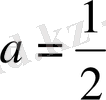 болғандағы
болғандағы
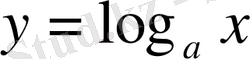 функциясының графиктеріне талдау жасай отырып, мынадай қорытындыларға келуге болады:
функциясының графиктеріне талдау жасай отырып, мынадай қорытындыларға келуге болады:
 болғанда: 1) функцияның анықталу облысы - оң нақты сандар жиыны:
болғанда: 1) функцияның анықталу облысы - оң нақты сандар жиыны:
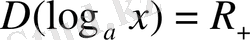 ; 2) функция мәндерінің жиыны - барлық нақты сандар жиыны:
; 2) функция мәндерінің жиыны - барлық нақты сандар жиыны:
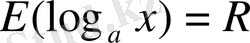 ; 3) функция бүкіл анықталу облысы бойында өседі, яғни
; 3) функция бүкіл анықталу облысы бойында өседі, яғни
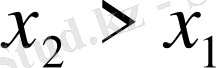 болғанда
болғанда
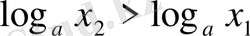 ; 4)
; 4)
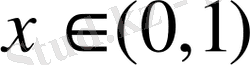 болғанда
болғанда
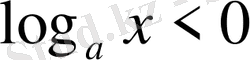 ;
;
 болғанда
болғанда
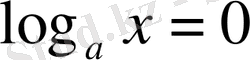 ;
;
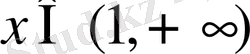 болғанда
болғанда
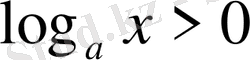 .
.
 болғанда: 1) функцияның анықталу облысы - оң нақты сандар жиыны:
болғанда: 1) функцияның анықталу облысы - оң нақты сандар жиыны:
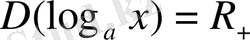 ; 2) функция мәндерінің жиыны - барлық нақты сандар жиыны:
; 2) функция мәндерінің жиыны - барлық нақты сандар жиыны:
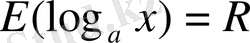 ; 3) функция бүкіл анықталу облысы бойында кемиді, яғни
; 3) функция бүкіл анықталу облысы бойында кемиді, яғни
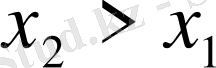 болғанда
болғанда
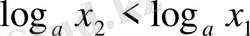 ; 4)
; 4)
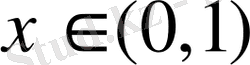 болғанда
болғанда
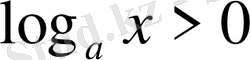 ;
;
 болғанда
болғанда
 ;
;
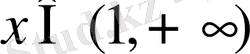 болғанда
болғанда
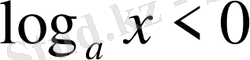 .
.
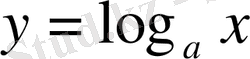 логарифмдік функциясының маңызды қасиеті - оның бүкіл анықталу облысында үзіліссіздігі.
логарифмдік функциясының маңызды қасиеті - оның бүкіл анықталу облысында үзіліссіздігі.
Мысалы,
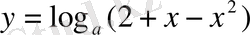 функциясының анықталу облысын табайық. Шешуі: логарифмдік функцияның анықталу облысы
функциясының анықталу облысын табайық. Шешуі: логарифмдік функцияның анықталу облысы
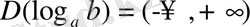 -ке тең және де, мұндағы
-ке тең және де, мұндағы
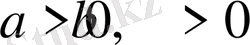 болатындықтан, келесідей теңсіздікті аламыз:
болатындықтан, келесідей теңсіздікті аламыз:
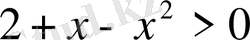 ;
;
 -ге көбейтеміз:
-ге көбейтеміз:
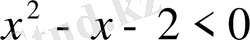 теңсіздігін шешеміз.
теңсіздігін шешеміз.
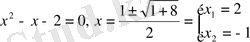 . СУРЕТ
. СУРЕТ
Жауабы:
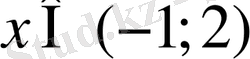 .
.
4. Тригонометриялық функциялар.
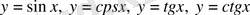 .
.
1.
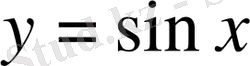 функциясы мәндерінің кестесін құрайық.
функциясы мәндерінің кестесін құрайық.
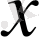
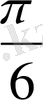
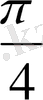
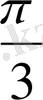
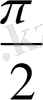
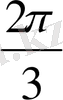
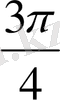
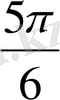

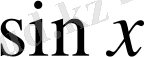
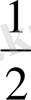
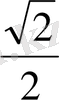
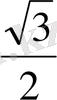
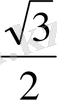
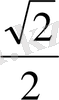
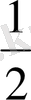
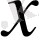
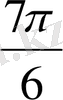
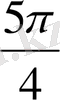
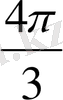
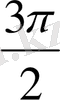
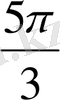
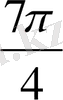
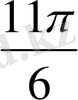

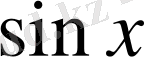
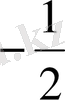
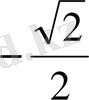
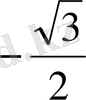
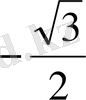
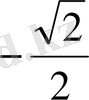
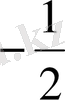
Жазықтықта тік бұрышты координаталар жүйесін алайық (12-сурет) . Координаттық жазықтықта кесте мәндеріне сәйкес нүктелерді белгілеп, оларды қисық сызық арқылы қосайық, сонда біз
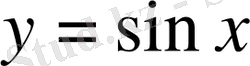 функциясының
функциясының
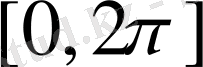 сегментіндегі графигін аламыз.
сегментіндегі графигін аламыз.
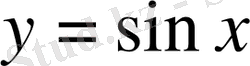 функциясы тақ функция болғандықтан, оның графигі координаттар бас нүктесіне қарағанда симметриялы болады. Ал
функциясы тақ функция болғандықтан, оның графигі координаттар бас нүктесіне қарағанда симметриялы болады. Ал
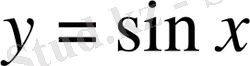 функциясы периодты
функциясы периодты
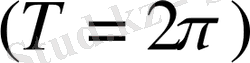 болғандықтан, оның графигі ұзындығы
болғандықтан, оның графигі ұзындығы
 болатын аралық сайын қайталанып отырады. Осылайша алынған қисық синусоида деп аталады да,
болатын аралық сайын қайталанып отырады. Осылайша алынған қисық синусоида деп аталады да,
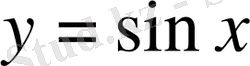 функциясының графигі болады.
функциясының графигі болады.
12-СУРЕТ
Графигі бойынша
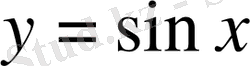 функциясының негізгі қасиеттерін атап өтейік.
функциясының негізгі қасиеттерін атап өтейік.
1)
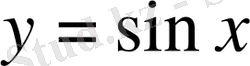 функциясы
функциясы
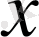 -ң барлық мәндерінде анықталған, яғни оның анықталу облысы бүкіл сандық ось
-ң барлық мәндерінде анықталған, яғни оның анықталу облысы бүкіл сандық ось
 болады.
болады.
2)
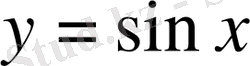 функциясының мәндері
функциясының мәндері
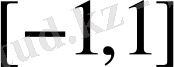 сегментінде жатады. Функцияның ең үлкен мәні 1-ге тең және ол
сегментінде жатады. Функцияның ең үлкен мәні 1-ге тең және ол
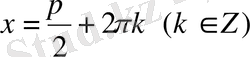 нүктелерінде қабылданады. Функцияның ең кіші мәні -1-ге тең және ол
нүктелерінде қабылданады. Функцияның ең кіші мәні -1-ге тең және ол
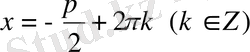 нүктелерінде қабылданады.
нүктелерінде қабылданады.
3)
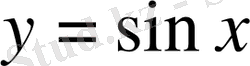 функциясы тақ функция:
функциясы тақ функция:
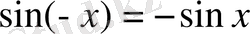 .
.
4)
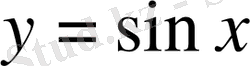 функциясы периодты функция, периоды
функциясы периодты функция, периоды
 .
.
5)
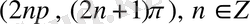 интервалдарында функция оң таңбалы, ал
интервалдарында функция оң таңбалы, ал
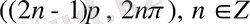 интервалдарында функция теріс таңбалы болады.
интервалдарында функция теріс таңбалы болады.
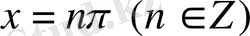 болғанда функция мәні нөлге тең болады. Бұл нүктелер
болғанда функция мәні нөлге тең болады. Бұл нүктелер
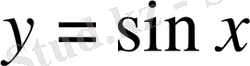 функциясының нөлдері деп аталады.
функциясының нөлдері деп аталады.
6)
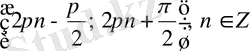 интервалдарында
интервалдарында
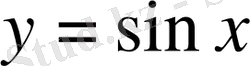 функциясы бірсарынды өседі де, ал
функциясы бірсарынды өседі де, ал
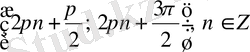 интервалдарында - бірсарынды кемиді.
интервалдарында - бірсарынды кемиді.
2.
 функциясының графигі.
функциясының графигі.
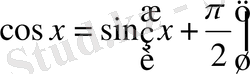 болғандықтан,
болғандықтан,
 функциясының графигі
функциясының графигі
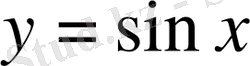 функциясының графигінен оны
функциясының графигінен оны
 осі бойымен солға қарай
осі бойымен солға қарай
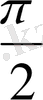 шамасына жылжыту арқылы алынады. Бұл қисықты (
шамасына жылжыту арқылы алынады. Бұл қисықты (
 функциясының графигін) косинусоида деп атайды (13-сурет) . Сонымен,
функциясының графигін) косинусоида деп атайды (13-сурет) . Сонымен,
 функциясының графигі солға қарай
функциясының графигі солға қарай
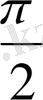 шамасына жылжытылған синусоида болады екен.
шамасына жылжытылған синусоида болады екен.
Графигі бойынша
 функциясының негізгі қасиеттерін де
функциясының негізгі қасиеттерін де
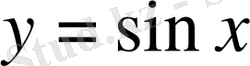 жағдайындағыдай етіп өтуге болады.
жағдайындағыдай етіп өтуге болады.
1)
 функциясы
функциясы
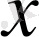 -ң барлық мәндерінде анықталған, яғни оның анықталу облысы бүкіл сандық ось
-ң барлық мәндерінде анықталған, яғни оның анықталу облысы бүкіл сандық ось
 болады.
болады.
2)
 функциясының мәндері
функциясының мәндері
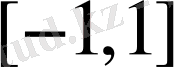 сегментінде жатады. Функцияның ең үлкен мәні 1-ге тең және ол
сегментінде жатады. Функцияның ең үлкен мәні 1-ге тең және ол
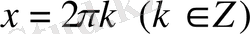 нүктелерінде қабылданады. Функцияның ең кіші мәні -1-ге тең және ол
нүктелерінде қабылданады. Функцияның ең кіші мәні -1-ге тең және ол
 нүктелерінде қабылданады.
нүктелерінде қабылданады.
3)
 функциясы жұп функция:
функциясы жұп функция:
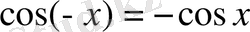 .
.
4)
 функциясы периодты функция, периоды
функциясы периодты функция, периоды
 .
.
5)
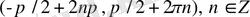 интервалдарында функция оң таңбалы, ал
интервалдарында функция оң таңбалы, ал
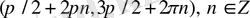 интервалдарында функция теріс таңбалы болады.
интервалдарында функция теріс таңбалы болады.
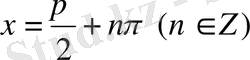 болғанда функция мәні нөлге тең болады. Бұл нүктелер
болғанда функция мәні нөлге тең болады. Бұл нүктелер
 функциясының нөлдері деп аталады.
функциясының нөлдері деп аталады.
6)
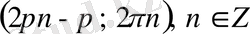 интервалдарында
интервалдарында
 функциясы бірсарынды өседі де, ал
функциясы бірсарынды өседі де, ал
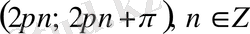 интервалдарында - бірсарынды кемиді.
интервалдарында - бірсарынды кемиді.
13-СУРЕТ
3.
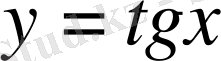 және
және
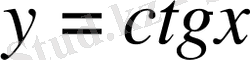 функцияларының графиктері.
функцияларының графиктері.
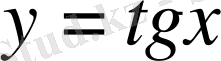 және
және
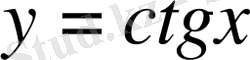 функциялары тақ функциялар, демек, олардың графиктері координаталар бас нүктесіне қатысты симметриялы болады. Бұл функциялардың периоды
функциялары тақ функциялар, демек, олардың графиктері координаталар бас нүктесіне қатысты симметриялы болады. Бұл функциялардың периоды
 екені белгілі.
екені белгілі.
Координаталық жазықтықта
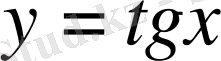 функциясы мәндеріне сәйкес нүктелерді салу үшін, осы функцияның бірнеше мәндерінің кестесін құрайық.
функциясы мәндеріне сәйкес нүктелерді салу үшін, осы функцияның бірнеше мәндерінің кестесін құрайық.
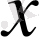
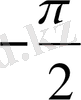
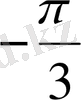
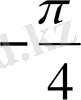
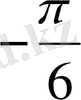
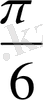
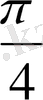
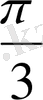
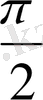
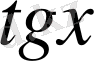

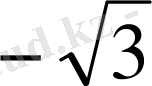
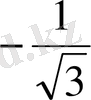
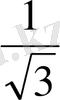
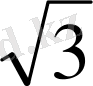
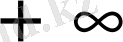
Енді осы нүктелерді белгілеп, оларды қисық сызық арқылы қосып,
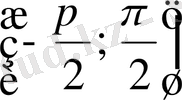 аралығында
аралығында
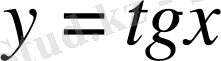 функциясының графигін саламыз.
функциясының графигін саламыз.
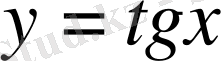 функциясы периодты болғандықтан,
функциясы периодты болғандықтан,
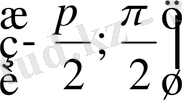 арасындағы графикті оңға қарай да, солға қарай да периодты жалғастырып, периодты
арасындағы графикті оңға қарай да, солға қарай да периодты жалғастырып, периодты
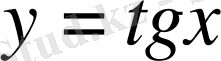 функциясының графигін аламыз (14-сурет) . Осы қисық тангенсоида деп аталады.
функциясының графигін аламыз (14-сурет) . Осы қисық тангенсоида деп аталады.
14-СУРЕТ
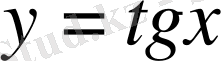 функциясының негізгі қасиеттері:
функциясының негізгі қасиеттері:
1)
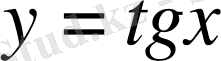 функциясы
функциясы
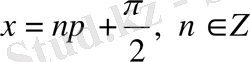 нүктелерінде анықталмаған. Функцияның анықталу облысы
нүктелерінде анықталмаған. Функцияның анықталу облысы
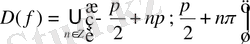 жиыны болады.
жиыны болады.
2)
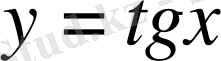 функциясы шенелмеген, оның мәндерінің жиыны
функциясы шенелмеген, оның мәндерінің жиыны
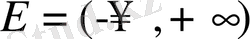 .
.
3)
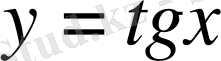 функциясы тақ функция, яғни тангенсоида координаталар бас нүктесіне қатысты симметриялы.
функциясы тақ функция, яғни тангенсоида координаталар бас нүктесіне қатысты симметриялы.
4)
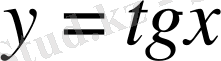 функциясы периодты функция
функциясы периодты функция
 , демек, оның графигі ұзындығы
, демек, оның графигі ұзындығы
 болатын аралық сайын қайталанып отырады.
болатын аралық сайын қайталанып отырады.
5)
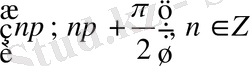 интервалында
интервалында
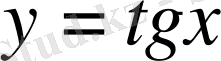 функциясы оң таңбалы, ал
функциясы оң таңбалы, ал
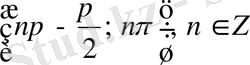 интервалдарында - теріс таңбалы. Анықталу облысына енетін барлық интервалдарды
интервалдарында - теріс таңбалы. Анықталу облысына енетін барлық интервалдарды
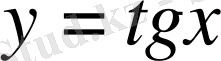 функциясы бірсарынды өседі.
функциясы бірсарынды өседі.
6)
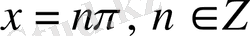 нүктелерінде
нүктелерінде
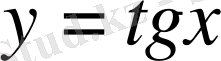 функциясының мәндері нөлге тең болады, бұл нүктелер функцияның нөлдері деп аталады.
функциясының мәндері нөлге тең болады, бұл нүктелер функцияның нөлдері деп аталады.
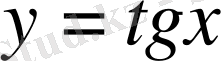 функциясы
функциясы
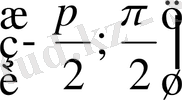 интервалында бірсарынды өсетінін және
интервалында бірсарынды өсетінін және
 -тен
-тен
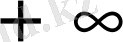 -ке дейінгі барлық мәндерін бір-бірден қабылдайтынын атап өтейік.
-ке дейінгі барлық мәндерін бір-бірден қабылдайтынын атап өтейік.
Координаталық жазықтықта
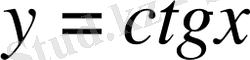 функциясы мәндеріне сәйкес нүктелерді салу үшін, осы функцияның бірнеше мәндерінің кестесін құрайық.
функциясы мәндеріне сәйкес нүктелерді салу үшін, осы функцияның бірнеше мәндерінің кестесін құрайық.
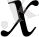
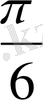
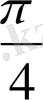
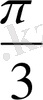
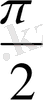
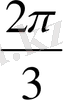
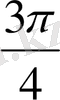
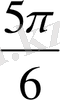

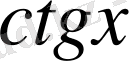
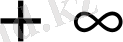
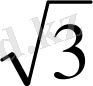
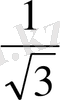
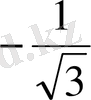
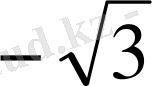

Енді осы нүктелерді белгілеп, оларды қисық сызық арқылы қосып,
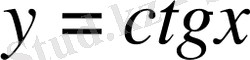 функциясының
функциясының
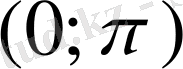 аралығындағы графигін аламыз. Функцияның периодтылығын пайдаланып, осы графикті оңға қарай да, солға қарай да периоды бойынша жалғастырып,
аралығындағы графигін аламыз. Функцияның периодтылығын пайдаланып, осы графикті оңға қарай да, солға қарай да периоды бойынша жалғастырып,
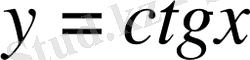 функциясының графигін аламыз (15-сурет) . Бұл қисық котангенсоида деп аталады.
функциясының графигін аламыз (15-сурет) . Бұл қисық котангенсоида деп аталады.
15-СУРЕТ
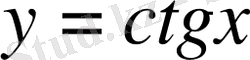 функциясының негізгі қасиеттері:
функциясының негізгі қасиеттері:
1)
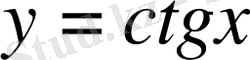 функциясы
функциясы
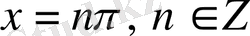 нүктелерінде анықталмаған, демек, оның анықталу облысы
нүктелерінде анықталмаған, демек, оның анықталу облысы
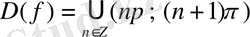 жиыны болады.
жиыны болады.
2)
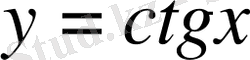 функциясы шенелмеген, мәндерінің жиыны -
функциясы шенелмеген, мәндерінің жиыны -
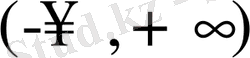 аралығы.
аралығы.
3)
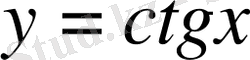 функциясы периодты функция
функциясы периодты функция
 , демек, оның графигі ұзындығы
, демек, оның графигі ұзындығы
 болатын аралық сайын қайталанып отырады.
болатын аралық сайын қайталанып отырады.
4)
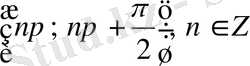 интервалдарында
интервалдарында
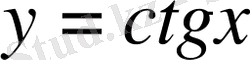 функциясы оң таңбалы, ал
функциясы оң таңбалы, ал
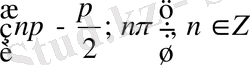 интервалдарында - теріс таңбалы болады. Анықталу облысына енетін барлық интервалдарда
интервалдарында - теріс таңбалы болады. Анықталу облысына енетін барлық интервалдарда
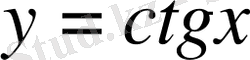 функциясы бірсарынды кемиді.
функциясы бірсарынды кемиді.
5)
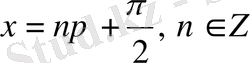 нүктелерінде
нүктелерінде
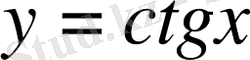 функциясы мәндері нөлге тең, бұл нүктелер функцияның нөлдері деп аталады.
функциясы мәндері нөлге тең, бұл нүктелер функцияның нөлдері деп аталады.
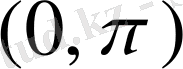 интервалында
интервалында
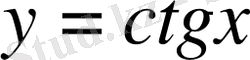 функциясы бірсарынды кемиді және
функциясы бірсарынды кемиді және
 -тен
-тен
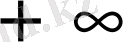 -ке дейінгі барлық мәндерін бір-бірден қабылдап шығады.
-ке дейінгі барлық мәндерін бір-бірден қабылдап шығады.
5. Кері тригонометриялық функциялар.
1.
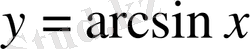 функциясы.
функциясы.
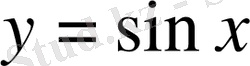 функциясын
функциясын
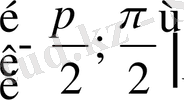 сегментінде қарастырайық. Функцияның осы аралықта бірсарынды өсетінін және -1-ден 1-ге дейінгі өзінің барлық мәндерін бір-бірден қабылдап өтетінін айтқан едік. Мысалы, егер
сегментінде қарастырайық. Функцияның осы аралықта бірсарынды өсетінін және -1-ден 1-ге дейінгі өзінің барлық мәндерін бір-бірден қабылдап өтетінін айтқан едік. Мысалы, егер
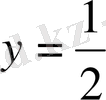 болса, онда
болса, онда
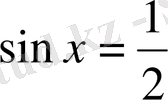 .
.
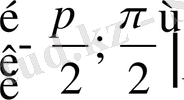 сегментінде
сегментінде
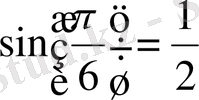 болатындай бір ғана
болатындай бір ғана
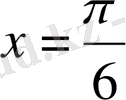 нүктесі бар. Сонымен, әрбір
нүктесі бар. Сонымен, әрбір
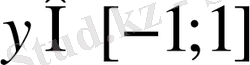 мәніне бір ғана
мәніне бір ғана
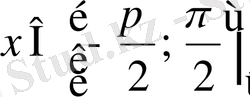 мәні сәйкес қойылады. Яғни,
мәні сәйкес қойылады. Яғни,
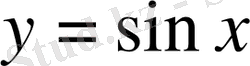 функциясы қайтымды функция (оның кері функциясы бар) .
функциясы қайтымды функция (оның кері функциясы бар) .
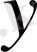 -ті
-ті
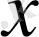 -ке және
-ке және
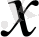 -ті
-ті
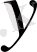 -ке ауыстырайық, сонда
-ке ауыстырайық, сонда
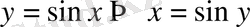 .
.
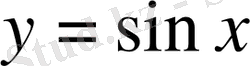 функциясына кері функция арксинус деп аталады да,
функциясына кері функция арксинус деп аталады да,
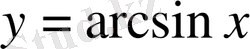 теңдігімен белгіленеді. (Ол былай оқылады:
теңдігімен белгіленеді. (Ол былай оқылады:
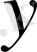 - синусы
- синусы
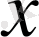 -ке тең болатын доға,
-ке тең болатын доға,
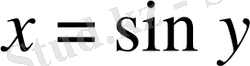 ) . Осы функцияның бірнеше мәндерін табайық.
) . Осы функцияның бірнеше мәндерін табайық.
 болсын. Сонда
болсын. Сонда
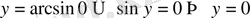 , өйткені
, өйткені
 . Егер
. Егер
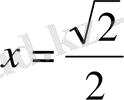 болса, онда
болса, онда
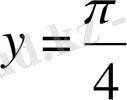 , өйткені
, өйткені
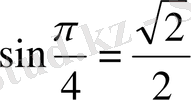 . Осылай табылған бірнеше мәндері бойынша кесте құрайық.
. Осылай табылған бірнеше мәндері бойынша кесте құрайық.
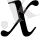
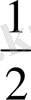
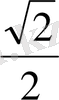
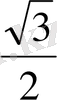
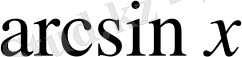
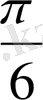
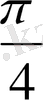
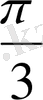
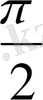
Координаталық жазықтықта
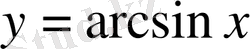 функциясы мәндеріне сәйкес келетін нүктелерді салайық.
функциясы мәндеріне сәйкес келетін нүктелерді салайық.
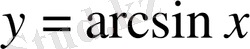 функциясының анықталу облысы
функциясының анықталу облысы
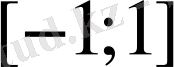 сегменті, яғни
сегменті, яғни
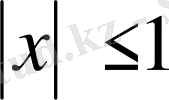 екені айқын. Функция мәндерінің облысы
екені айқын. Функция мәндерінің облысы
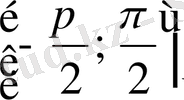 сегменті,
сегменті,
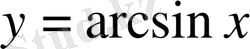 функциясы тақ функция, периодты емес.
функциясы тақ функция, периодты емес.
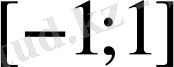 аралығында бірсарынды өседі (16-сурет) .
аралығында бірсарынды өседі (16-сурет) .
16-СУРЕТ
Мысал.
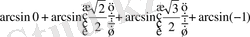 өрнегін есептеу керек.
өрнегін есептеу керек.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz