Матрицалар алгебрасы: негізгі ережелер мен амалдар


МАЗМҰНЫ
беті
Кіріспе . . . 4
I - Бөлім МАТРИЦАЛАР АЛГЕБРАСЫНЫҢ НЕГІЗГІ ЕРЕЖЕЛЕРІ . . . 5
1. 1 Матрица ұғымы. Негізгі түсініктер . . . 5
1. 2 Матрицаларды қарапайым түрлендіру жолдары . . . 8
1. 3 Матрицаларды қосу, алу және сандарға көбейту . . . 9
1. 4 Матрицаларды өзара көбейту . . . 10
1. 5 Матрицаны транспонирлеу . . . 12
II - Бөлім МАТРИЦАЛАР АЛГЕБРАСЫНЫҢ АМАЛДАРЫ . . . 15
2. 1 Кері матрица . . . 15
2. 2 Матрицаның абсолютті шамасы және нормасы . . . 17
2. 3 Матрицаның рангысы . . . 19
2. 4 Үшбұрышты матрицалар . . . 23
2. 5 Анықтауыштарды есептеу . . . 28
Қортынды . . . 32
Әдебиеттер . . . 32
КІРІСПЕ
Матрицалар алгебрасы қазіргі кезде сандық әдістерге байланысты жаңа алгоритмдермен дамуда. Күн жүйесі планеталарының орнықтылығы, атом реакторларының беріктігі, газ, мұнай, кен өндірісі, гидротехника, жер қыртысының орнықтылығы, жерсілкінісінің аймақтары, жер асты, жер бетінің сейсмоберік құрылыстары, оқу процесі, өмірдің тағы басқа көптеген салаларында кең қолданылып, әрі уақыт өткен сайын қатты қарқынмен дамып келе жатқан қазіргі заманғы математикалық аса қуатты сандық әдістердің бірі шекті элементтер әдісі (ШЭӘ) . Бұл әдістің негізі матрицалар алгебрасына байланысты. Бүгіндері матрицалар алгебрасы жеке пән ретінде де шекті элементтер негізінде де университеттердің оқу жоспарларына негізгі пәндердің бірі ретінде толық енді. Дж. Норри мен Ж. де Фриздің 1976 жылға дейінгі мәліметтері бойынша шекті элементтер әдісіне арналып 17752 жұмыс жарияланған болса, бүгіндері оны санау мүмкін де емес әрі мағынасы да жоқ. Бұл әдіс математикада қашан, қалай пайда болды деген тарихына қысқаша тоқалайық. Оның алғашқы белгілері Рицтің (1909), Галеркиннің (1915), Куранттың(1943), Прагер мен Сингтің (1947), Аргиристің (1954 - 1955), Тернердің (1956) жұмыстарынан басталады. Шекті элементтер туралы ең алғашқы ұғым мен түсінікті 1956 - Тернер енгізді. Ал «шекті элементтер» терминін (1960) Клафф енгізді.
1960 - жылдардан соң ШЭӘ - нің дамуына Зенкевич, Аргирис, Айронс, Андерсон, Оден, Галлагер тағы басқа американдық мамандардың үлесі көп. Бұл әдістің даму барысын бір ізге, жүйеге түсіріп, іс жүзінде қолдануға лайықтап оқулықтар мен монографиялар жазған Зенкевич, Батье, Вильсон, Оден, Стренг, Фикс, Норри; Фриз, Галлагер, Сегерлиндтердің сіңірген еңбектері айрықша. ШЭӘ - нің негізін баяндаудағы біздің басты мақсатымыз - оны түсініп, игерудің, қарапайым есептерді шешуге, дипломдық және күндізгі және сыртқы бөлім студенттерінің, ғылыми жұмыстарына ғана емес сонымен қатар мектеп оқушыларының олимпиадаларға қатынасуларына дайындалуда да төте жолдармен қолданып игерулеріне мүмкіндік жасау. Сондықтан негізгі теңдеулер мен формулаларды, өрнектерді матрицалық түрде жазумен қатар оларды толық ашып, тікелей программалауға қолайлы болуы үшін матрицалық алгоритмдер түрінде баяндалды.
I - Бөлім МАТРИЦАЛАР АЛГЕБРАСЫНЫҢ НЕГІЗГІ ЕРЕЖЕЛЕРІ
1. 1 Матрица ұғымы. Негізгі түсініктер.
Нақты немесе комплексті (түбір астында теріс сандар)
 қатардан және
қатардан және
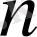 тік жолдардан тұратын сандардың кестесін
матрица
деп атайды. Оның түрі төмендегі
тік жолдардан тұратын сандардың кестесін
матрица
деп атайды. Оның түрі төмендегі
(1) - ші өрнектегідей
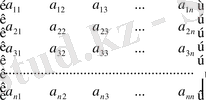 (1)
(1)
Бірінші өрнектегідегі матрицаның әрбір элементі оның қатары немесе элеименті деп аталады. Индекстерді қысқаша
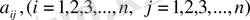 деп белгілесек, онда (1) матрицаның әрбір саны оның элементі деп аталады. Мұндағы
деп белгілесек, онда (1) матрицаның әрбір саны оның элементі деп аталады. Мұндағы
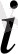 матрицаның әрбір қатарының нөмірін, ал
матрицаның әрбір қатарының нөмірін, ал
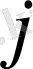 оның тік жолдарының нөмірін көрсетеді. Бірінші өрнекті тік және жатық жолдарының нөмірлерін
оның тік жолдарының нөмірін көрсетеді. Бірінші өрнекті тік және жатық жолдарының нөмірлерін
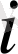 және
және
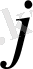 деп көрсетіп мынадай түрде де жазуға болады
деп көрсетіп мынадай түрде де жазуға болады
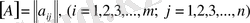
Егер
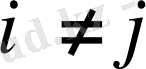 болғанда
болғанда
 болса ондай матрицаны
диагоналдық
деп атайды.
болса ондай матрицаны
диагоналдық
деп атайды.
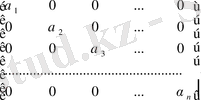
Егер оның диагоналындағы элементтердің мәні 1 - тең болса, онда оны бірлік матрица деп атайды

Соңғы матрицаны Кронекер символы арқылы былай да жазуға болады.

Немесе
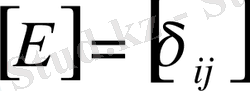
Бұдан мынадай теңдіктер шығады.
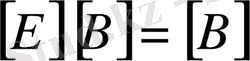 ,
,
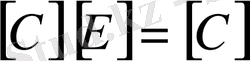 ,
,
 .
.
Нөлдік матрица ұғымы.
Барлық элементтері нөлден тұратын, өлшемі
 болатын матрицаны
болатын матрицаны
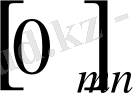 нөлдік матрица
деп атайды. Оның кейбір мысалдары төмендегідей:
нөлдік матрица
деп атайды. Оның кейбір мысалдары төмендегідей:
 ,
,
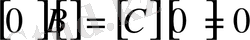 .
.
Келесі бір анықтама - матрицаның анықтауышы деген ұғыммен байланысты. Ол мынадай түрде жазылады (немесе белгіленеді) . Сиректеу де болса мынадай түрде де жазылады
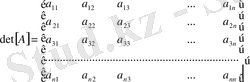
Сондай - ақ былай деп те белгіленеді
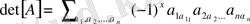
Шындығында соңғы түрдегі символ тым сирек қолдданылады.
Матрица түрлері әртүрлі болып келеді. Мәлімет ретінде олардың кейбір түрлерін шартты атаулармен келтіре кетейік.
1. Сирек толтырылған матрица
2. Диагоналдық матрица
3. Симметриялық матрица (егер
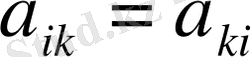 болса)
болса)
4. Антисимметриялық (егер
 болса)
болса)
5. Нөлдік матрица
6. Бірлік матрица
7. Диагоналдық басым матрица
8. Оң анықталған матрица
9. Ленталық матрица
10. Екі диагоналдық матрица
11. Үш диагоналдық матрица
12. Квазидиагоналдық
13. Жоғарғы үшбұрышты матрица
14. Төменгі үшбұрышты матрица
15. Эрмиттік (түйіндес) матрица (
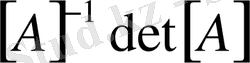 )
)
16. Теріс анықталған матрица
17. Транспонирленген матрица
18. Кері матрица
19. Тіркеме матрица
20. Шаршы матрица
21. Тік бұрышты матрица
22. Қарама - қарсы матрица
23. Торкөздік матрица
24. Сәйкес (эквивалентті) матрицалар
25. Айналдыру матрицасы (Якоби бойынша түрлендіру матрицасы)
26. Шекті матрица
27. Шексіз матрица
28. Мономиалдық матрица
29. Сингулярлық матрица (ерекше)
30. Ерекше емес матрица
31. Қалыпты матрица (нормальная)
32. Унитарлық матрица (
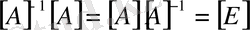 )
)
33. Эквивалентті матрица
34. Ортогоналдық матрица тағы сол сияқты. Біз бұл жерде матрицаның барлық түрлеріне анықтама беріп тоқтала алмаймыз. Бұл тақырыптың өзі арнайы үлкен курс. Аталған матрица түрлерінің кейбірінің анықтамалары, ерекшеліктері, оларға қолданылатын амалдар төменде баяндалады. Ал кейбірі шекті элементтер бөлімінде толық баяндалады. Төменде мысал ретінде осылардың бірі - мономиалдық матрица түрі көрсетіліп отыр.

Мономиалдық матрицада әрбір жатық жолы мен әрбір тік жолында нөл емес бір ғана элемент болады да қалғандары нөлден құралады.
1. 2 Матрицаларды қарапайым түрлендіру жолдары
Матрицаларды түрлендірудің төмендегі түрлері қарапайым түрге жатады.
1. екі жатық немесе екі тік жолдарды өзара ауыстыру
2. кез - келген тік немесе жатық жолдың элементтерін нөлден өзге бір санға көбейту.
3. жатық немесе тік жолдардың элементтерін түгелдей бір санға көбейтіп, басқа бір жолдың элементтеріне мүшелеп қосу немесе азайту.
Бір матрица екінші матрицаны шексіз қарапайым түрлендірулер арқылы алынған болса онда ондай екі матрицаны эквивалентті деп атайды. Олар өзара тең бола бермесе де рангылары тең болады.
Шаршы
 матрицасын әрбір қарапайым түрлендіру оны ерекшелігі жоқ белгілі бір матрицаға көбейтумен тең.
матрицасын әрбір қарапайым түрлендіру оны ерекшелігі жоқ белгілі бір матрицаға көбейтумен тең.
Мысалы
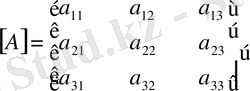
матрицасының екінші және үшінші жатық жолдарының орындарын ауыстырып, эквивалентті
 матрицасын аламыз.
матрицасын аламыз.
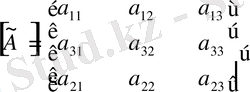
Осы матрицаны басқа жолмен де алуға болады. Ол үшін бірлік
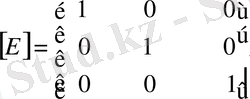
матрицасының екінші және үшінші жолдарының орындарын ауыстырамыз.
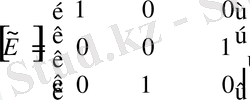
Енді осы матрицаны
 матрицасының сол жағына қойып көбейтейік. Сонда
матрицасының сол жағына қойып көбейтейік. Сонда
 матрицасын аламыз.
матрицасын аламыз.
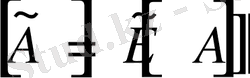
Өзге қарапайым түрлендірулер де осыған ұқсас жолдармен жүзеге асырылады. Мысалы
 теңдігіндегі
теңдігіндегі
 және
және
 матрицаларының қатарларын
матрицаларының қатарларын
 матрицасы
матрицасы
 матрицасына айналғанша түрлендңре берсек, онда
матрицасына айналғанша түрлендңре берсек, онда
 теңдігіне келеміз. Ұндағы
теңдігіне келеміз. Ұндағы
 бірлік түрге айналдырылған матрица. Бұдан
бірлік түрге айналдырылған матрица. Бұдан
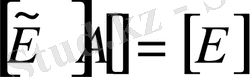 екенін ескеріп,
екенін ескеріп,
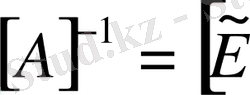 теңдігін аламыз. Яғни кері матрица
теңдігін аламыз. Яғни кері матрица
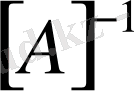 түрлендірілген бірлік матрица болып шығады. Кері матрицаны қатарларды түрлендіру арқылы табу осы амалдарға негізделген.
түрлендірілген бірлік матрица болып шығады. Кері матрицаны қатарларды түрлендіру арқылы табу осы амалдарға негізделген.
1. 3 Матрицаларды қосу, алу және сандарға көбейту
Егер
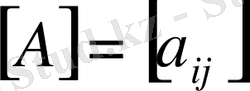 және
және
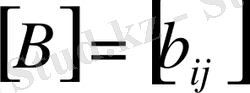 болып
болып
 болса онда
болса онда
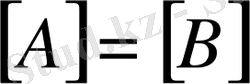 , яғни екі матрица өзара тең. Екі матрицаның
, яғни екі матрица өзара тең. Екі матрицаның
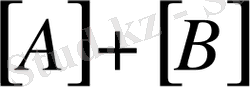 қосындысы үшінші
қосындысы үшінші
 матрицасына тең. Оның әрбір элементі
матрицасына тең. Оның әрбір элементі
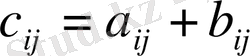
Матрицаларды қосу және алу ережелер
1.

2.

3. Қосуға байланысты мынадай қасиеттер бар:
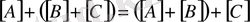 ;
;
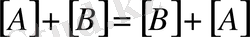 ;
;
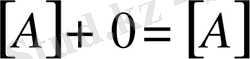 .
.
4. Матрицаны санға көбейту
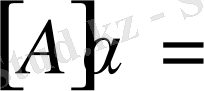
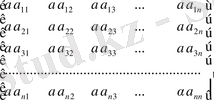
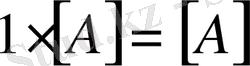 ;
;
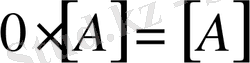 ;
;
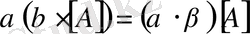 ;
;
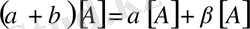 ;
;
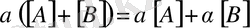
Мұндағы
 - сандар. Егер
- сандар. Егер
 -ның өлшемі
-ның өлшемі
 болса, онда
болса, онда
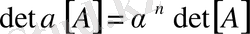 .
.
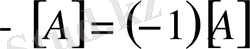 - қарама -қарсы матрица деп аталады.
- қарама -қарсы матрица деп аталады.
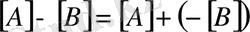
1. 4 Матрицаларды өзара көбейту
Мынадай екі матрица берілсін
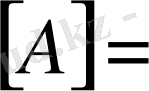

және
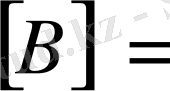
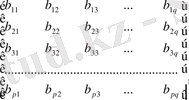
Мұндағы
 -ның өлшемі
-ның өлшемі
 дағын
дағын
 матрицасының өлшемі
матрицасының өлшемі
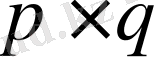 . Егер
. Егер
 матрицасының қатарының саны
матрицасының қатарының саны
 матрицасының тік жолдарының санына тең болса
матрицасының тік жолдарының санына тең болса
 болады- дағын бұл екі матрицаның көбейтіндісі
болады- дағын бұл екі матрицаның көбейтіндісі
 өлшемді үшінші бір
өлшемді үшінші бір
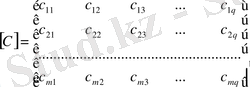
 матрицасына тең болады.
матрицасына тең болады.
 .
.
Қортынды матрицаның элементтерін мынадай алгортиммен жазайық.
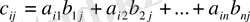 .
.
Соңғы өрнектегі
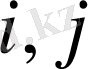 индекстерінің мәндері былай өзгереді.
индекстерінің мәндері былай өзгереді.
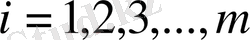 ,
,
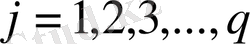 . Сонымен мынадай ереже шығады. Екі матрицаны көбейту үшін олардың біріншісінің жатық жолдарын екіншісінің тік жолдарымен көбейтіп, мүшелеп қосамыз.
. Сонымен мынадай ереже шығады. Екі матрицаны көбейту үшін олардың біріншісінің жатық жолдарын екіншісінің тік жолдарымен көбейтіп, мүшелеп қосамыз.
1 - мысал.

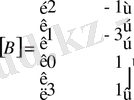
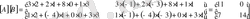
2 - мысал.
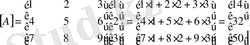
Бұрынғы оқулықтарда матрицаға да векторға да бір ғана
 символы қолданылып келген еді. Соңғы кездерде векторға арнайы
символы қолданылып келген еді. Соңғы кездерде векторға арнайы
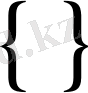 символы қолданылуда. Бұдан былай осы символды қолданайық. Сонда жоғарыдағы 2 - мысал былай жазылады.
символы қолданылуда. Бұдан былай осы символды қолданайық. Сонда жоғарыдағы 2 - мысал былай жазылады.
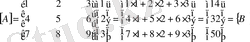
Ережелер:
1.
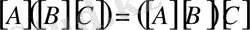
2.
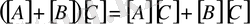
3.
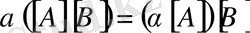
4.
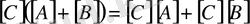
Үшінші жолдағы
 - сан
- сан
5.
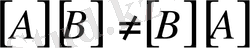
Соңғы ережеге оңай көз жеткізуге болады.
3 - мысал.
 ,
,
 болсын.
болсын.
Сонда бұлардың көбейтінділері мынадай болады.
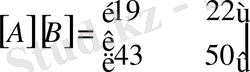 ,
,
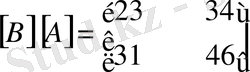 .
.
Демек бұдан
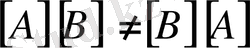 екенін көреміз. Сондай -ақ
екенін көреміз. Сондай -ақ
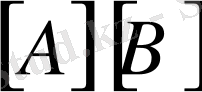 көбейтіндісі бар болып
көбейтіндісі бар болып
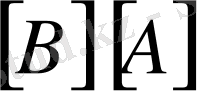 көбейтіндісі мүлдем болмауы мүмкін. Ондай жағдайға төмендегі матрицалар мысал бола алады.
көбейтіндісі мүлдем болмауы мүмкін. Ондай жағдайға төмендегі матрицалар мысал бола алады.
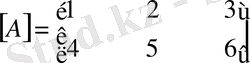 ,
,
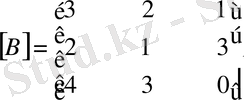
Екеуі өзара көбейтіледі:
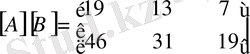 , ал
, ал
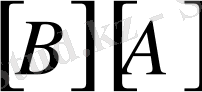 жоқ.
жоқ.
1. 5 Матрицаны транспонирлеу
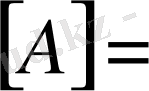

Берілген

 матрицасының тік жолдарын жатық жолдармен алмастырсақ, онда транспонирленген
матрицасының тік жолдарын жатық жолдармен алмастырсақ, онда транспонирленген
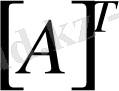 матрицасын аламыз.
матрицасын аламыз.
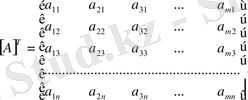
Вектор
 жатық жолдың транспонирленген векторы тік жол болады.
жатық жолдың транспонирленген векторы тік жол болады.
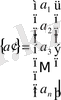
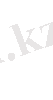
Транспонирленген матрицаның қасиеттері:
1. екі рет транспонирленген матрица бастапқы матрицаға сәйкес келеді:
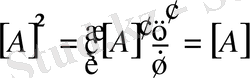 ;
;
2. транспонирленген матрицалардың қсындысы ол матрицалардың
қосындыларының транспонирленуіне тең.
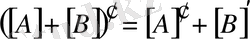 ;
;
3. матрицалардың көбейтінділерінің транспонирленуі оларды керісінше
орналастырып, транспонирленген көбейтінділеріне тең.
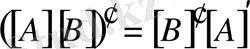
Егер
 матрицасы шаршылы (квадратты болса), онда
матрицасы шаршылы (квадратты болса), онда
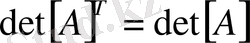
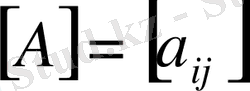 матрицасы өзінің транспонирленген матрицасына тең болса онда ол матрица симметриялы еп аталады, яғни
матрицасы өзінің транспонирленген матрицасына тең болса онда ол матрица симметриялы еп аталады, яғни
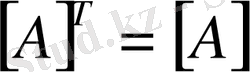 . (2)
. (2)
(2) - теңдіктен мыдай тұжырымдар шығады. Біріншіден, симметриялық матрица шаршылы
 , екіншіден, оның диагоналға қатысты симметриялы элементтері өзара тең.
, екіншіден, оның диагоналға қатысты симметриялы элементтері өзара тең.

Бұл айтылғандардан

екенін көреміз. Себебі
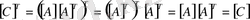
Мысал.
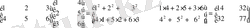
II - Бөлім МАТРИЦАЛАР АЛГЕБРАСЫНЫҢ АМАЛДАРЫ
2. 1 Кері матрица
1 - ші анықтама. Берілген матрицаға кері матрица дегеніміз оны бастапқы матрицаға оң жағынан болсын, сол жағынан болсын көбейткенде нәтижесінде бірлік матрица шығатын матрицаны айтады. Берілген
 матрицасына кері матрицаны
матрицасына кері матрицаны
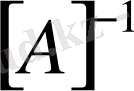 деп белгілейік. Сонда анықтама бойынша
деп белгілейік. Сонда анықтама бойынша
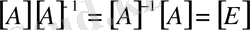 (3)
(3)
Мұндағы
 - бірлік матрица. Берілген матрицаға кері матрицаны табу дегенді кейде бастапқы матрицаны
айналдыру деп те айтады
.
- бірлік матрица. Берілген матрицаға кері матрицаны табу дегенді кейде бастапқы матрицаны
айналдыру деп те айтады
.
2- ші анықтама. Егер шаршы матрицаның анықтауышы нөлден өзгеше сан болса онда оны ерекше емес матрица деп атайды. Егер анықтауышы нөл болса, онда оны ерекше немесе сингулярлы матрица деп атайды.
Т е о р е м а. Кез - келген ерекше емес матрицаның кері матрицасы болады.
Д ә л е л д е у і.
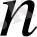 - ші ретті ерекше емес
- ші ретті ерекше емес
 матрицасы берілсін дейік.
матрицасы берілсін дейік.
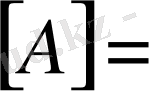

Бұл матрицаның анықтауышын нөл емес дейік, яғни
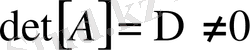
Осы матрица үшін тіркеме немесе одақтас матрица құрайық.
 (4)
(4)
Мұндағы
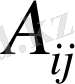 - дегеніміз
- дегеніміз
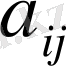 -дің сәйкес элементтерінің алгебралық толықтауыштары (таңбаларымен алынған минорлар) . Бұл терминдер туралы кеңірек түсініктер алдағы бөлімшелерде кеңірек айтылады.
-дің сәйкес элементтерінің алгебралық толықтауыштары (таңбаларымен алынған минорлар) . Бұл терминдер туралы кеңірек түсініктер алдағы бөлімшелерде кеңірек айтылады.
Алгебралық толықтауыштар (4) - өрнекте транспонирленіп орналасқанына көңіл бөліңіз. Бұл матрицаның барлық элементін бастапқы матрицаның анықтауышының шамасы
 -ға немесе
-ға немесе
 -ға бөлеміз.
-ға бөлеміз.
 (5)
(5)
Соңғы (5) - ші өрнек
 -ға кері матрица екенін (
-ға кері матрица екенін (
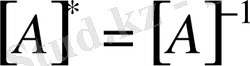 ) дәлелдейік. Біріншіден, матрицаның кез - келген жатық немесе тік жолының элементтерінің әрқайсысына тән алгебралық толықтауыштарына көбейтінділерінің қосындысы матрицаның анықтауышы екені белгілі. Екіншіден, кез - келген жатық немесе тік жолының элементтерінің параллель қатарлардың алгебралық толықтауыштарына көбейтінділерінің қосындысы нөл болады. Осы айтылғандарды математикалық өрнек түрінде жазайық.
) дәлелдейік. Біріншіден, матрицаның кез - келген жатық немесе тік жолының элементтерінің әрқайсысына тән алгебралық толықтауыштарына көбейтінділерінің қосындысы матрицаның анықтауышы екені белгілі. Екіншіден, кез - келген жатық немесе тік жолының элементтерінің параллель қатарлардың алгебралық толықтауыштарына көбейтінділерінің қосындысы нөл болады. Осы айтылғандарды математикалық өрнек түрінде жазайық.
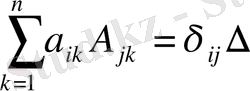
және
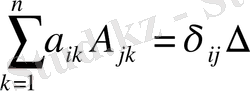 ,
,
мұндағы
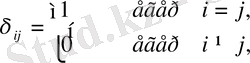
 .
.
Осындай қасиеттерді ескере отырып,
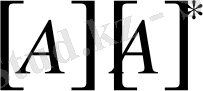 көбейтіндісін жазайық
көбейтіндісін жазайық
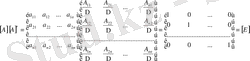
Сонымен
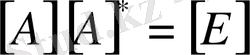 екенін дәлелдедік. Енді нақты мысал келтірейік.
екенін дәлелдедік. Енді нақты мысал келтірейік.
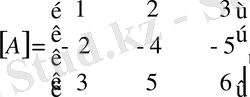
матрицасына кері матрицаны табу керек.
Ш е ш у і. Алдымен анықтауышы
 - ны табайық.
- ны табайық.
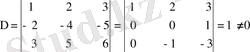
Демек
 матрицасы ерекше емес.
матрицасы ерекше емес.
Тіркеме матрицаны құрайық.
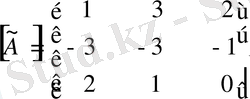
Бұл матрицаның барлық элементтерін
 -ге бөлсек, кері матрица
-ге бөлсек, кері матрица
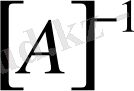 -ді табамыз.
-ді табамыз.
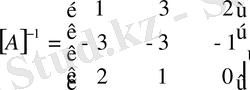
2. 2 Матрицаның абсолютті шамасы және нормасы
Матрицаның нормасы оның абсолюттік шамасы (модулі) түсінігімен тікелей байланысты. Сондықтан алдымен матрицаның абсолютті шамасы түсінігімен танысайық.
Бірдей типтегі
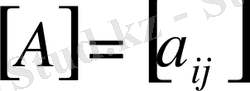 және
және
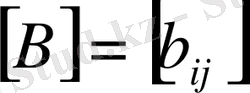 матрицалары үшін
матрицалары үшін
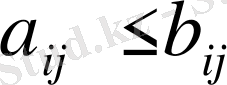
болса, онда
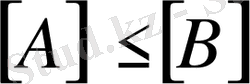
Бұл жағдай кез - келген екі матрицаны өзара салыстыруға болмайды деген сөз.
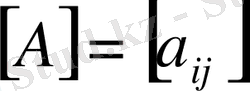 матрицасының
абсолют шамасы (модулі)
деп
матрицасының
абсолют шамасы (модулі)
деп
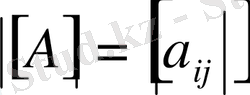
ді айтамыз. Мұндағы
 дегеніміз
дегеніміз
 матрицасы элементтерінің модулі.
матрицасы элементтерінің модулі.
Егер
 және
және
 матрицалары үшін
матрицалары үшін
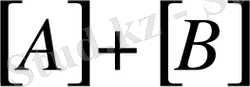 және
және
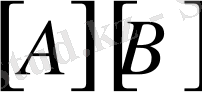 амалдары орындалатын болса, онда:
амалдары орындалатын болса, онда:
а)
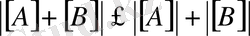 ;
;
б)
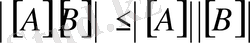 ;
;
в)
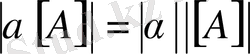 , (
, (
 - сан) ;
- сан) ;
г)
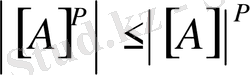 , (
, (
 - натурал сан) .
- натурал сан) .
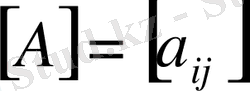 матрицасының нормасы
дегеніміз төмендегі шарттарды қанағаттандыратын
матрицасының нормасы
дегеніміз төмендегі шарттарды қанағаттандыратын
 шын саны:
шын саны:
а)
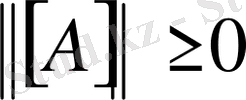 , егер
, егер
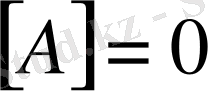 болса ғана
болса ғана
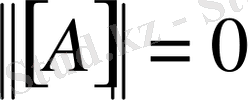 ;
;
б)
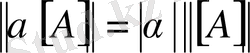 , (
, (
 - сан) ;
- сан) ;
в)
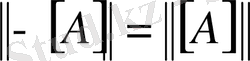 ;
;
г)
 ;
;
д)
 ;
;
Шаршы матрица үшін
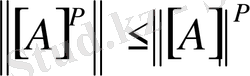 , (
, (
 - натурал сан) . Төмендегі белгілі қағидаларды дәлелсіз келтірейік:
- натурал сан) . Төмендегі белгілі қағидаларды дәлелсіз келтірейік:
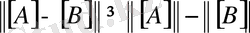 ;
;
егер
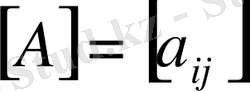 болса, онда
болса, онда
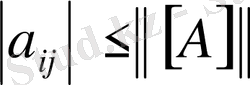 ;
;
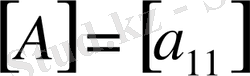 скалярлық матрицасы үшін
скалярлық матрицасы үшін
 ;
;
егер
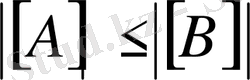 болса, онда
болса, онда
 , дербес жағдайда
, дербес жағдайда
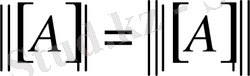 .
.
Кез - келген типтегі
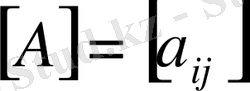 матрицасы үшін оңай есептелінетін норманың мынадай
матрицасы үшін оңай есептелінетін норманың мынадай
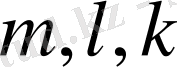 деп аталатын негізгіүш түрі бар:
деп аталатын негізгіүш түрі бар:
1.
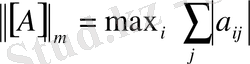 (
(
 -норма) ;
-норма) ;
2.
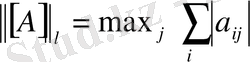 (
(
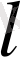 -норма) ;
-норма) ;
3.
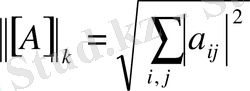 (
(
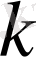 -норма)
-норма)
М ы с а л.
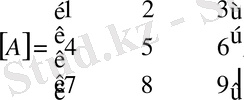 матрицасының
матрицасының
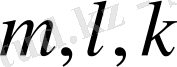 нормаларын табайық.
нормаларын табайық.
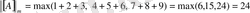
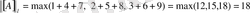

 -ның (
-ның (
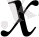 - векторының)
- векторының)
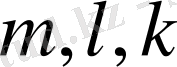 нормалары былай табылады.
нормалары былай табылады.
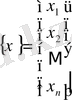
үшін
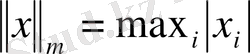 ;
;
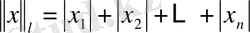 ;
;

2. 3 Матрицаның рангысы
Мынадай тік бұрышты матрицаны қарастырайық.
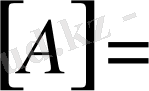

Осы матрицадан кез-келген жолмен
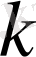 жатық жолдар мен
жатық жолдар мен
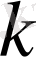 тік жолдарды таңдайық
тік жолдарды таңдайық
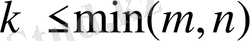 . Осылардың қиылыстарымен қоршалған элементтер шаршы матрица құрайды. Осы соңғы матрицаның анықтауышын бастапқы
. Осылардың қиылыстарымен қоршалған элементтер шаршы матрица құрайды. Осы соңғы матрицаның анықтауышын бастапқы
 матрицасының
матрицасының
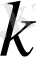 -шы ретті миноры деп аталады.
-шы ретті миноры деп аталады.
А н ы қ т а м а. Матрицанының рангысы дегеніміз матрицаның нөлден өзге ең жоғары ретті миноры.
Басқаша айтқанда
 матрицасының
матрицасының
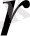 рангысы болады, егер:
рангысы болады, егер:
1. кем дегенде нөлден өзге
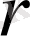 -ші ретті бір миноры болса;
-ші ретті бір миноры болса;
2.
 матрицасының
матрицасының
 және одан да жоғары ретті барлық минорлары нөлге тең болса.
және одан да жоғары ретті барлық минорлары нөлге тең болса.
Нөлдік матрицаның, яғни барлық элементтері нөлден тұратын матрицаның
рангысы нөл деп аталады.
Жоғарыдағы матрицаның өлшемдерін көрсететін
 және
және
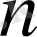 екі санның қайсысы кіші болса, сонымен матрица рангысының айрымы матрицаның
кемістігі (дефектісі)
деп аталады. Егер кемістік нөлге тең болса, онда матрицаның рангысы мүмкін деген ең жоғарғы мәнге ие болады.
екі санның қайсысы кіші болса, сонымен матрица рангысының айрымы матрицаның
кемістігі (дефектісі)
деп аталады. Егер кемістік нөлге тең болса, онда матрицаның рангысы мүмкін деген ең жоғарғы мәнге ие болады.
Матрицаның рангысын табу үшін мынадай ережелерге сүйенген пайдалы:
1. минорды ең кіші бірінші ретінен бастап, жоғарғы реттеріне біртіндеп табу керек.
2. реті
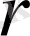 болатын нөлден өзге
болатын нөлден өзге
 минорын таптық дейік. Онда
минорын таптық дейік. Онда
 -ны қамтитын
-ны қамтитын
 -ші минорларды ғана табу жеткілікті. Егер ол минорлардың бәрі де нөлге тең болса, онда матрицаның рангысы
-ші минорларды ғана табу жеткілікті. Егер ол минорлардың бәрі де нөлге тең болса, онда матрицаның рангысы
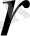 -ге тең. Егер олардың тым болмағанда біреуі нөлге тең болмай шықса, онда амалды соған қолдану керек. Әрине ондай жағдайда матрицаның рангысы
-ге тең. Егер олардың тым болмағанда біреуі нөлге тең болмай шықса, онда амалды соған қолдану керек. Әрине ондай жағдайда матрицаның рангысы
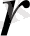 -ден үлкен болады.
-ден үлкен болады.
1-ші м ы с а л.
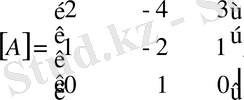 матрицасының рангысын табу керек.
матрицасының рангысын табу керек.
Ш е ш у і.
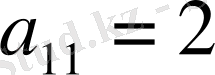 екенін байқаймыз. Демек
екенін байқаймыз. Демек
 матрицасының рангысы бірден кем деген сөз. Енді оның алғашқы екі жатық жолымен екі тік жолдарын қамтитын элементтерден матрица құрып, анықтауышын табайық.
матрицасының рангысы бірден кем деген сөз. Енді оның алғашқы екі жатық жолымен екі тік жолдарын қамтитын элементтерден матрица құрып, анықтауышын табайық.
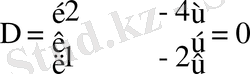
Енді бастапқы матрицаның екінші, үшінші жатық жолдарымен бірінші, екінші тік жолдарын қамтитын элементтерден матрица құрып, анықтауышын табайық.
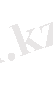
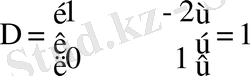
Демек бастапқы матрицаның рангысы кем дегенде екіге тең.
Матрицаның рангысын түрлі минорларын есептемей де табуға болады. Ол үшін берілген матрицаны төмендегідей қарапайым түрлендірулер арқылы диагоналдық түрге келтіреміз.
1. екі қатарды немесе екі тік жолды өзара орын алмастыру арқылы
2. қатарды немесе тік жолды нөлден өзге кез -келген санға көбейту
3. бір жолдағы элементтерді нөлден өзге бір санға көбейтіп барып екінші жолдағы элементтерге қосу, немесе тік жолдарға қолдану.
Нәтижесінде диагоналдағы нөл емес сандардың саны матрицаның рангысын көрсетеді.
2-ші м ы с а л.
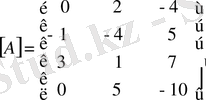 матрицасының рангысын табу керек.
матрицасының рангысын табу керек.
Ш е ш у і. Бұл матрицаның бірінші екінші тік жолдарының орындарын ауыстырып, одан соң бірінші жолды
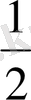 ге көбейтіп бірінші элементі
ге көбейтіп бірінші элементі
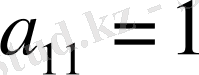 болатын мына түрдегі матрицаны аламыз.
болатын мына түрдегі матрицаны аламыз.
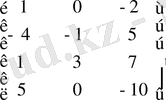
Бірінші тік жолды
 -ге көбейтіп, үшінші тік жолға қосып, төмендегі түрге келеміз.
-ге көбейтіп, үшінші тік жолға қосып, төмендегі түрге келеміз.
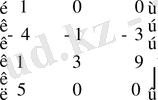
Енді бұл матрицаны екінші жолдан бастап төмен қарай түрлендіреміз. Бірінші жолды
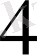 -ке көбейтіп, екінші жолға қосамыз. Одан соң бірінші жолды
-ке көбейтіп, екінші жолға қосамыз. Одан соң бірінші жолды
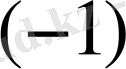 -ге көбейтіп, үшінші жолға қосамыз. Әрі қарай бірінші жолды
-ге көбейтіп, үшінші жолға қосамыз. Әрі қарай бірінші жолды
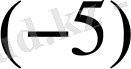 -ке көбейтіп, төртінші қатарға қосамыз. Сонда матрицаның мына түріне келеміз.
-ке көбейтіп, төртінші қатарға қосамыз. Сонда матрицаның мына түріне келеміз.
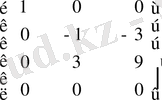
Енді бірінші тік жол мен бірінші жатық жолды өзгертпей, қалған жолдарға амалдар қолданамыз: 1. екінші қатарды
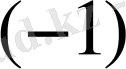 -ге көбейтеміз;
-ге көбейтеміз;
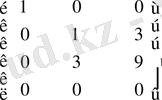
2. екінші қатарды
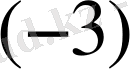 -ке көбейтіп, үшінші жолға қосамыз;
-ке көбейтіп, үшінші жолға қосамыз;
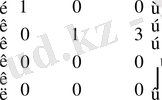
3. екінші тік жолды
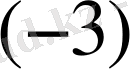 -ке көбейтіп, үшінші тік жолға қосамыз.
-ке көбейтіп, үшінші тік жолға қосамыз.
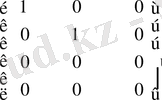
Соңғы матрицаның түрі диагоналдық. Басты диагоналындағы бір деген сандардың саны екеу. Демек бұл матрицаның, яғни бастапқы матрицаның рангы екіге тең.
3-ші м ы с а л.
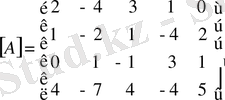 матрицасының рангысын табу керек.
матрицасының рангысын табу керек.
Ш е ш у і. Сол жақ бұрышындағы екінші ретті минордан бастайық. Оның анықтауышы нөл екенін бірден байқаймыз. Бірақ
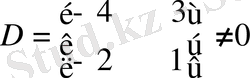 және оны қоршаған үшінші ретті минор
және оны қоршаған үшінші ретті минор
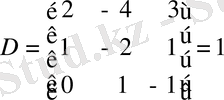
 минорын қоршаған төртінші ретті екі минор да нөлге тең:
минорын қоршаған төртінші ретті екі минор да нөлге тең:
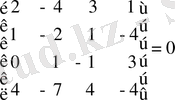 ;
;
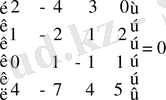 .
.
Сонымен берілген матрицаның рангысы үшке тең де, кемістігі 4 -3=1.
2. 4 Үшбұрышты матрицалар
А н ы қ т а м а. Үшбұрышты матрица дегеніміз диагоналдың үстіңгі немесе астыңғы элементтері нөлге тең шаршы матрицаны айтады.
Мысалы,
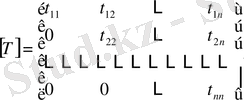 ,
,
бұл жерде
 болғанда
болғанда
 болғандықтан жоғарғы үшбұрышты матрица деп аталады. Осы сияқты
болғандықтан жоғарғы үшбұрышты матрица деп аталады. Осы сияқты
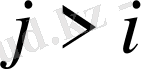 болғанда
болғанда
 болса, онда ол төменгі үшбұрышты матрица болады. Оны
болса, онда ол төменгі үшбұрышты матрица болады. Оны
 деп белгілейік.
деп белгілейік.
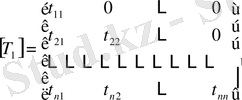
Бұл өрнектерге қарағанда диагоналдық матрица үшбұрышты матрицаның дербес жағдайы екендігі көрінеді.
Үшбұрышты матрицаның анықтауышы оның диагоналдық элементтерінің көбейтіндісіне тең:
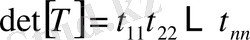
Үшбұрышты матрицаның диагоналындағы элементтер арасында тым болмағанда бір нөлдік элемент кездессе онда ол ерекше (сингулярлы) матрица болатындығын байқау қиын емес. Тағы мынадай ерекшеліктерді келтірейік.
1. Элементтерінің мәндері әртүрлі екі жоғарғы үшбұрышты матрицаны қоссақ немесе көбейтсек нәтижесінде жоғарғы үшбұрышты матрица шығады. Төменгі үшбұрышты матрица үшін де осы қасиет орындалады.
2. Үшбұрышты матрицаға кері матрица да құрылымы дәл сондай үшбұрышты матрица болады. Егер шаршы немесе тік бұрышты матрицаны үшбұрышты матрицаларға жіктей алсақ, онда бастапқы матрицаға кері матрицаны табу оңай. Осы айтылғандар алгебралық теңдеулер жүйесін шешу үшін аса қажетті мәселе. Бұл жерде тік бұрышты матрица үшбұрышты матрицаға қалай жіктеледі деген заңды сұрақ туады. Қарапайым аксиома түрінде мүмкін емес болып көрінетін мұндай жіктеу шындығында мүмкін. Оны дәлелдеп көрсету оңай. Оның сыры мынада. Шекті элементтер әдісінде тым қарапайым жағдайда болмаса
 өлшемді
өлшемді
 матрицасы (шаршы матрица)
матрицасы (шаршы матрица)
 өлшеммен тік бұрышты матрица түрінде симметриялы етіп құрылады. Себебі компьютердің жадысынан аз орын алады да есептеу әлдеқайда тез орындалады. Тік бұрышты матрицада диагоналдық элементтердің орындары белгілі болғандықтан үшбұрышты матрицаға жіктеу амалдары орындала береді. Қорыта айтқанда тік бұрышты матрицаны үшбұрышты матрицаға жіктегенде оның шаршы матрицаға сәйкес келетін диагоналдық элементтерінің орындары арқылы жүзеге асырылады.
өлшеммен тік бұрышты матрица түрінде симметриялы етіп құрылады. Себебі компьютердің жадысынан аз орын алады да есептеу әлдеқайда тез орындалады. Тік бұрышты матрицада диагоналдық элементтердің орындары белгілі болғандықтан үшбұрышты матрицаға жіктеу амалдары орындала береді. Қорыта айтқанда тік бұрышты матрицаны үшбұрышты матрицаға жіктегенде оның шаршы матрицаға сәйкес келетін диагоналдық элементтерінің орындары арқылы жүзеге асырылады.
1 - ші м ы с а л. Берілген үшбұрышты
 матрицасына кері матрица табу керек
матрицасына кері матрица табу керек
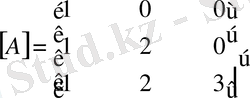
Ш е ш у і. Ізделініп отырған әзірше белгісіз кері матрица элементтерін
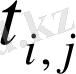 деген белгісіздермен белгілейік.
деген белгісіздермен белгілейік.
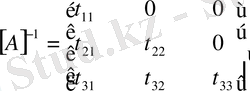
 және
және
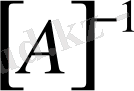 матрицаларын өзара көбейтейік
матрицаларын өзара көбейтейік
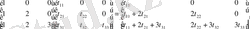
Кері матрица ережесі бойынша бурілген матрицаны өзінің кері матрицасына көбейтсек бірлік
 матрицасы шығатынын алдыңғы тақырыптардан білеміз.
матрицасы шығатынын алдыңғы тақырыптардан білеміз.
Демек
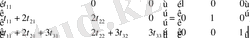
Енді екі матрицаның элементтерін мүшелеп теңестіреміз.
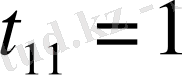 ,
,
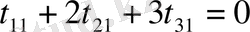 ,
,
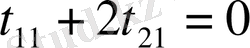 ,
,
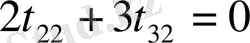 ,
,
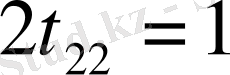 ,
,
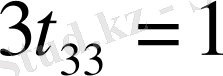 .
.
Бұл теңдеулерден белгісіз
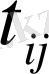 -лерді біртіндеп табамыз.
-лерді біртіндеп табамыз.
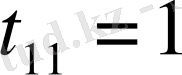 ,
,
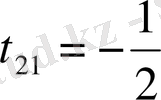 ,
,
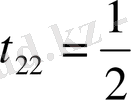 ,
,
 ,
,
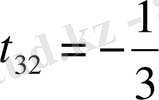 ,
,
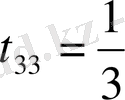 .
.
Олай болса ізделініп отырған кері матрица
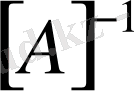 -ның элементтері табылды.
-ның элементтері табылды.
Сонымен

Берілген
 матрицасы мен соңғы шыққан
матрицасы мен соңғы шыққан
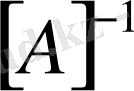 матрицасын өзара көбейтсе бірлік
матрицасын өзара көбейтсе бірлік
 матрицасы шығатынын тексеріп көріңіз.
матрицасы шығатынын тексеріп көріңіз.
Байқасаңыз бұл мысалда бастапқы матрицның өзі үшбұрышты матрица. Ал шындығында кез - келген шаршы матрицаны да үшбұрышты матрицаға жіктей білу керек. Сондықтан аса маңызды мына бір теореманы келтірейік.
Т е о р е м а. Басты диагоналдық минорлары нөлден өзгеше болатын яғни
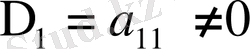 ;
;
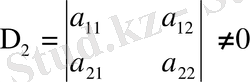 ; . . .
; . . .
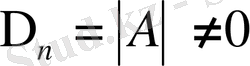 ,
,
кез - келген шаршы
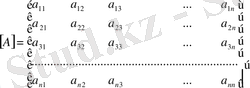
матрицасын түзілімдері әртүрлі жоғарғы және төменгі екі үшбұрышты матрицалардың көбейтіндісі түріне бірден бір жолмен келтіруге болады, егер олардың біреуінің диагоналдық элементтерін өзгермейтіндей етіп белгілесек, мысалы
 ге теңестірсек.
ге теңестірсек.
Бұл теореманың дәлелдеуін келтірмей-ақ, үшбұрышты матрицаларды табудың әдісін келтірейік. Ізделініп отырған төменгі үшбұрышты матрицаны
 деп, жоғарғы үшбұрышты матрицаны
деп, жоғарғы үшбұрышты матрицаны
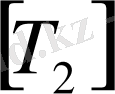 деп белгілейік.
деп белгілейік.
Сонда
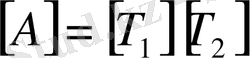 , (6)
, (6)
мұндағы
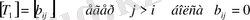 (7)
(7)
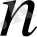 - ші ретті төменгі үшбұрышты матрица.
- ші ретті төменгі үшбұрышты матрица.
Сол сияқты
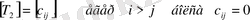 (8)
(8)
Бұл матрицаларды (6) -шы формула бойынша көбейтіп, нәтижесін алгоритмдік түрде жазайық.
 (9)
(9)
Соңғы (9) жүйе (7) -ші және (8) -ші шарттар бойынша мынадай түрге келеді.
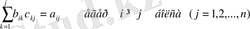 (
(
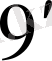 )
)
және
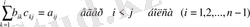 (
(
 )
)
Соңғы (
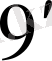 ) және (
) және (
 ) өрнектердің мағынасын тереңірек айқындау үшін
) өрнектердің мағынасын тереңірек айқындау үшін
 дейік
дейік
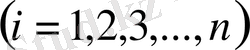 .
.
2 - ші м ы с а л. Берілген шаршы
 матрицасын
матрицасын
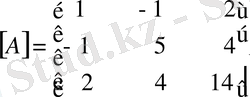
 және
және
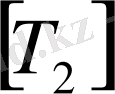 матрицаларының көбейтінділеріне жіктеу керек.
матрицаларының көбейтінділеріне жіктеу керек.
Ш е ш у і.
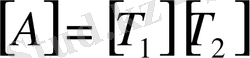 . (10)
. (10)
 мен
мен
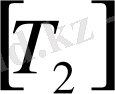 -ні мына түрде іздейміз
-ні мына түрде іздейміз
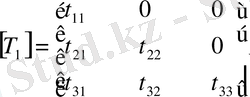 және
және
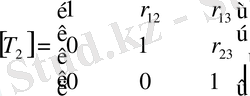
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz